基于动力学系统的最优潮流问题可行域刻画

江出阳，江晓东

（1.天津大学电气自动化与信息工程学院，天津 300072；2.美国康奈尔大学电气与计算机工程学院，伊萨卡 14853）

基于动力学系统的最优潮流问题可行域刻画

江出阳1，江晓东2

（1.天津大学电气自动化与信息工程学院，天津 300072；2.美国康奈尔大学电气与计算机工程学院，伊萨卡 14853）

可行域问题是最优潮流问题中的一个基础和重要问题。由于非线性约束的存在，最优潮流问题的可行域通常很复杂。针对如上情况，本文提出了一种非双曲的动力学系统，并用其稳定平衡流形对最优潮流问题的可行域进行了完整刻画。同时，本文通过理论和数值分析验证了所提方法的有效性。最后，应用动力学系统的稳定平衡流形对最优潮流问题的可行域进行可视化，并进一步研究最优潮流问题的可行域在不同约束参数下的变化情况。

最优潮流；可行域；动力学系统；稳定平衡流形

自从1962年Carpentier[1]第1次提出电力系统中的网络约束经济调度问题，最优潮流问题就受到广泛的关注和研究。最优潮流问题已经成为电力系统分析中的一项基本工具。而且，如何解决最优潮流问题也是电力市场经济和可靠运行的核心问题。最优潮流问题从本质上来看是一个带有约束的非凸非线性优化问题。过去的几十年来，众多学者提出了很多确定性方法和智能启发式算法来解决最优潮流问题，主要包括线性规划法、二次规划法、非线性规划法、牛顿法、内点法、神经网络、遗传算法[2]、进化算法、粒子群优化算法和凸松弛法等[3]。但是，鲜有涉及最优潮流问题中的一个基础和重要的问题—可行域问题。最优潮流问题的可行域定义在控制变量空间上，在该空间上，最优潮流问题的一系列等式约束和不等式约束条件都能够得到满足。在最优潮流中有线性约束（主要是框式约束）和非线性约束两种约束条件。由于非线性约束的存在，最优潮流的可行域一般是非凸的，而且有时是不连续的，由几个道路连通的可行部分构成，在每个可行部分上至少存在一个局部最优解。文献[4]通过数值计算验证了最优潮流问题的可行域确实是非凸的。文献[5]研究了一些特定网络下可行注入空间的几何结构。

需要特别指出的是，在电力系统中还有另外一个重要的“域”概念，即静态安全域（也称可行域）。电力系统的静态安全域由Hnyilicza等[6]在1975年首次提出。安全域定义在潮流方程的功率注入空间上，在此空间上系统是静态安全的。从安全域的概念提出以来，有很多文献在研究用解析的方法近似估计静态安全域[7]。文献[8-11]对安全域的方法学和应用进行了深入的研究，并取得了大量具有工程实用价值的研究成果。为了实现安全域概念的实用化和可视化，开发了3种实用的安全域，分别是实用动态安全域、静态电压稳定的安全域和实用小扰动稳定安全域。但是需要注意的是，电力系统的安全域与最优潮流问题的可行域有很大的区别。安全域定义在功率注入空间上，而最优潮流的可行域定义在控制变量空间上，控制变量包括PV节点的有功功率输出和电压幅值、平衡节点的电压幅值等。简单来说，可行域与最优潮流的约束集密切相关，而安全域则与功率注入空间上的安全分析密不可分。

很显然，如果可行域是空集，那么最优潮流问题将无解。而且如果可行域不存在，上述提到的任一方法在求解最优潮流问题时都将发散。因此，可行域的特性对最优潮流算法的收敛特性具有很大影响。除了2节点系统[12]，最优潮流问题的可行域很难解析地表达。本文利用一种非双曲动力学系统的稳定平衡流形对最优潮流问题的可行域进行刻画，并进一步研究等式约束和不等式约束中的参数对可行域的影响。

1 最优潮流问题可行域定义

最优潮流问题的约束集定义如下：

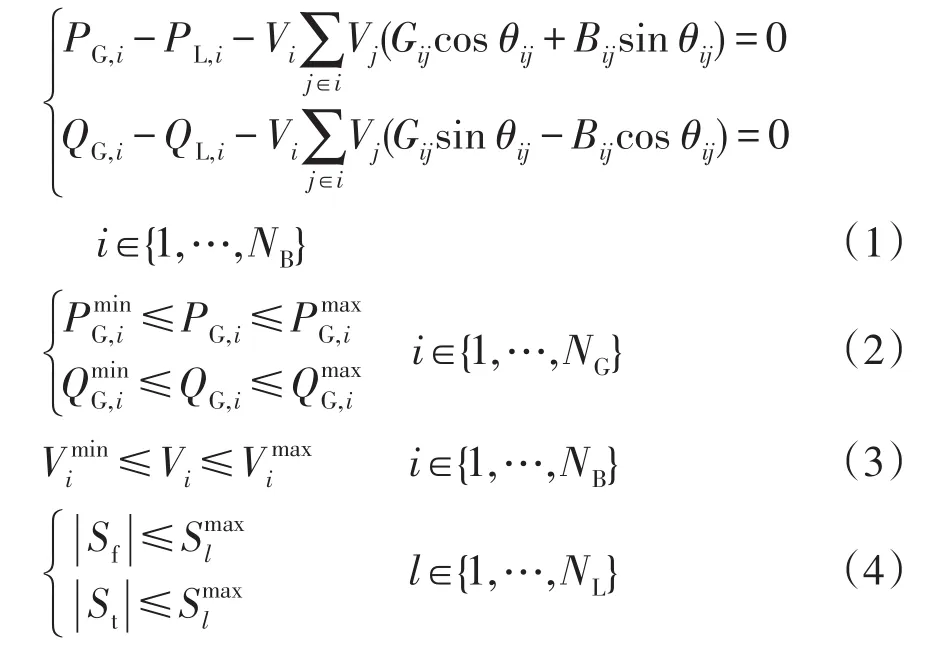
式中：NB为系统节点数；NG为系统发电机台数；NL为系统传输线路数；Gij和Bij分别为节点i到节点j的线路等效电导和等效电纳；PL，i和QL，i分别为节点i的有功负荷和无功负荷；θi为节点i的电压相角，θij=θi-θj；θref为平衡节点的电压相角，θref设为常数；Vi为节点i的电压幅值；PG，i和QG，i分别为节点i的发电机有功功率输出和无功功率输出；Sf为线路l首端视在功率；St为线路l末端视在功率。

式（1）为电力系统分析和计算中最重要的潮流方程，式（2）为发电机有功功率和无功功率出力的物理限制，电压幅值的工作范围如式（3）所示，式（4）为线路潮流的热极限。最优潮流问题中的变量可以分为控制变量（u）和状态变量（v）。其中控制变量包括PV节点的有功功率输出和电压幅值、平衡节点的电压幅值、移相器、变压器分接头、并联电容器等。如果将移相器、变压器分接头、并联电容器等设备考虑进模型时，则最优潮流问题将变为一个混合整数的非线性规划问题，这也是我们未来的研究方向之一，但是考虑到问题复杂性以及目前算法的局限性，在本文中，暂不考虑离散的控制变量，所以控制变量的个数为NG+(NG-1)=2NG-1，即所有发电机节点的电压幅值加上PV节点有功功率输出。所有其他的变量即为状态变量，状态变量可由控制变量和潮流方程（1）导出。至于表达式Sf和St，其可由状态变量和控制变量共同地表达出。

为简单起见，式（1）～式（4）可简化为

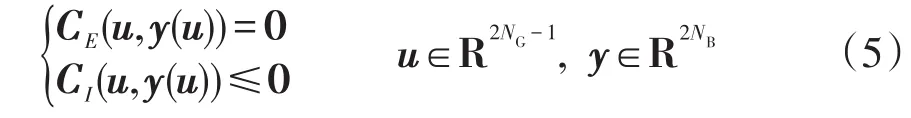
式中：CE=(c1,…,c2NB)T；CI=(c2NB+1,…,c4NG+4NB+2NL)T。

利用变换技术可以将式（5）中的不等式转换为等式。在这里，直接将松弛变量s加入到不等式约束中：

基于如上转换，最优潮流问题中的约束方程可以完整表示为

式中，H=(h1,…,hm)T:Rn→Rm，n=6NG+4NB+2NL-1，m=4NG+4NB+2NL。

定义1最优潮流问题的可行域。

最优潮流问题的可行域FR定义在控制变量空间上，在该空间上，最优潮流问题的一系列等式约束和不等式约束条件都能够得到满足，即

由于非线性约束的存在，最优潮流问题的可行域FR一般是非凸的，而且有时是不连续的，由几个道路连通的可行部分构成，即

式中：FRi为第i个道路连通的可行部分；K为可行部分的总数。

2 非线性动力学系统概述

一类非双曲动力学系统定义为

式中，H:Rn→Rm，M:Rn→Rn×m,m≤n。

定义2稳定平衡流形。

对于一个伪双曲平衡流形Σ[13]，如果Σ上的任意一点x∈Σ，DF(x)在正规空间Nx(Σ)上的特征向量所对应的特征值的实部都为负值，则Σ是一个稳定平衡流形SEM（stable equilibrium manifold）；否则，Σ是一个不稳定平衡流形UEM（unstable equilibrium manifold），特别地，如果一个伪双曲平衡流形Σ有k个正的特征值所对应的特征向量在正规空间Nx(Σ)上，则Σ被称作k型不稳定平衡流形（type-kUEM）。

3 最优潮流问题可行域的刻画

首先利用最优潮流问题的等式约束与不等式约束（7），构造一个非双曲动力学系统，即

式中，DH(x)为方程组H(x)的雅可比矩阵。

将系统（11）命名为商梯度系统，是一个非线性、非双曲的动力学系统。

文献[13]中已经证明，约束集（7）的可行域与系统（11）的稳定平衡流形之间存在着密切的关系，如以下两个定理所示。

定理1可行域与稳定平衡流形。

假定约束集（7）的可行域由一些不连通的可行部分构成。那么FRi，即约束集（7）的一个可行部分，是商梯度系统（11）的一个稳定平衡流形，记作关系式为

因此，最优潮流问题的可行域可以利用系统（11）的稳定平衡流形进行完整刻画。然而，系统（11）的稳定平衡流形中可能包含如下所定义的退化稳定平衡流形。

定义3退化稳定平衡流形。

对于商梯度系统（11）的一个稳定平衡流形Σs，如果 H(Σs)≠0 且 DH(Σs)TH(Σs)=0 ，那么Σs被称作退化稳定平衡流形。

显然，当Σs是退化稳定平衡流形时，rank(DH(Σs))＜m。相反，非退化（或常规）稳定平衡流形满足H(Σs)=0。

定理2可行域的刻画。

约束集（7）的可行部分与商梯度系统（11）的常规稳定平衡流形一一对映，即

接下来，利用一个2节点系统[14]来数值验证定理2。2节点系统的可行域及其所对应的商梯度系统的稳定平衡流形的数值计算结果及对比情况如图1所示。

图1 2节点系统可行域与稳定平衡流形的关系Fig.1 Relationship between the feasible region and stable equilibrium manifolds of a 2-bus system

图1（a）中的可行域是将目标函数设定为常数后通过内点法计算得出的，图1（b）中稳定平衡流形的获得方法详见文献[13]。在此算例中，可行域和稳定平衡流形是等价的。

4 算例分析

本节将通过数值计算分别求出一些测试算例的可行域和与之相对应的商梯度系统的稳定平衡流形，从而对定理1和定理2进行进一步的数值验证。然后，将应用稳定平衡流形研究在如下条件下最优潮流问题的可行域的变化情况：①不同的电压约束；②不同的线路潮流约束；③不同的负荷情况。

4.1 可行域与稳定平衡流形关系

根据定理1和定理2，最优潮流问题的可行域可以由商梯度系统的稳定平衡流形完全刻画。但是为了对可行域进行可视化，仍然需要对初始点进行采样以获得稳定平衡流形。为了以直接的方式计算可行域和稳定平衡流形，首先利用拉丁超立方采样技术均匀地采样大量点，例如，在以下测试系统中的变量上下限区间内采样了10 000个点。然后，以这些点为初始点，通过对系统（11）进行积分，最终获得大量稳定平衡流形上的点。拉丁超立方技术能够对搜索空间进行均匀的采样，因此，虽然无法证明，但对于小系统，只要采样数足够大，所有的稳定平衡流形都能够被搜寻到。

在这里，对文献[14]中的9节点系统进行测试，该算例由3台发电机和9条线路构成。由于在最优潮流问题中，最受关注的控制变量即为发电机的有功输出，因此对于该9节点系统，将在PG投影平面上展示其可行部分和稳定平衡流形。图2中的数值结果表明，该9节点系统具有3个不连通的可行部分，这3个可行部分包含了4个最优潮流解。其中，局部最优解和全局最优解分别用标记‘×’和‘○’表示。针对图2，通过观察得到如下结论：①每个可行部分对应一个稳定平衡流形；②图2（b）中存在一个退化稳定平衡流形（孤立点），该点不是一个可行点。

上述数值研究与定理1和定理2的阐述一致，证实了动力学系统（11）的（非退化）稳定平衡流形能够完整刻画最优潮流问题的可行域。

图2 9节点系统的可行域与稳定平衡流形的关系Fig.2 Relationship between the feasible region and stable equilibrium manifolds of a 9-bus system

4.2 不等式约束中参数对可行域的影响

最优潮流问题中通常有两类不等式约束：框式约束和非线性约束（线路潮流约束）。所以在本节中，将对这两类约束进行分别讨论。在不失一般性的情况下，对于框式约束，在本节中仅考虑电压约束。

4.2.1 电压约束

在这里将对第3节提到的2节点系统进行测试，在2节点系统中，电压边界默认为0.95 p.u.～1.05 p.u.。在以下测试中，边界将逐渐收紧，以观察可行域会发生什么变化。

从图3可以看出，当电压边界收紧时，常规稳定平衡流形将沿电压轴方向被切割。同时，当常规稳定平衡流形消失时，退化稳定平衡流形（图3（c）和图3（d）中的孤立点）将出现并取代原来的位置。

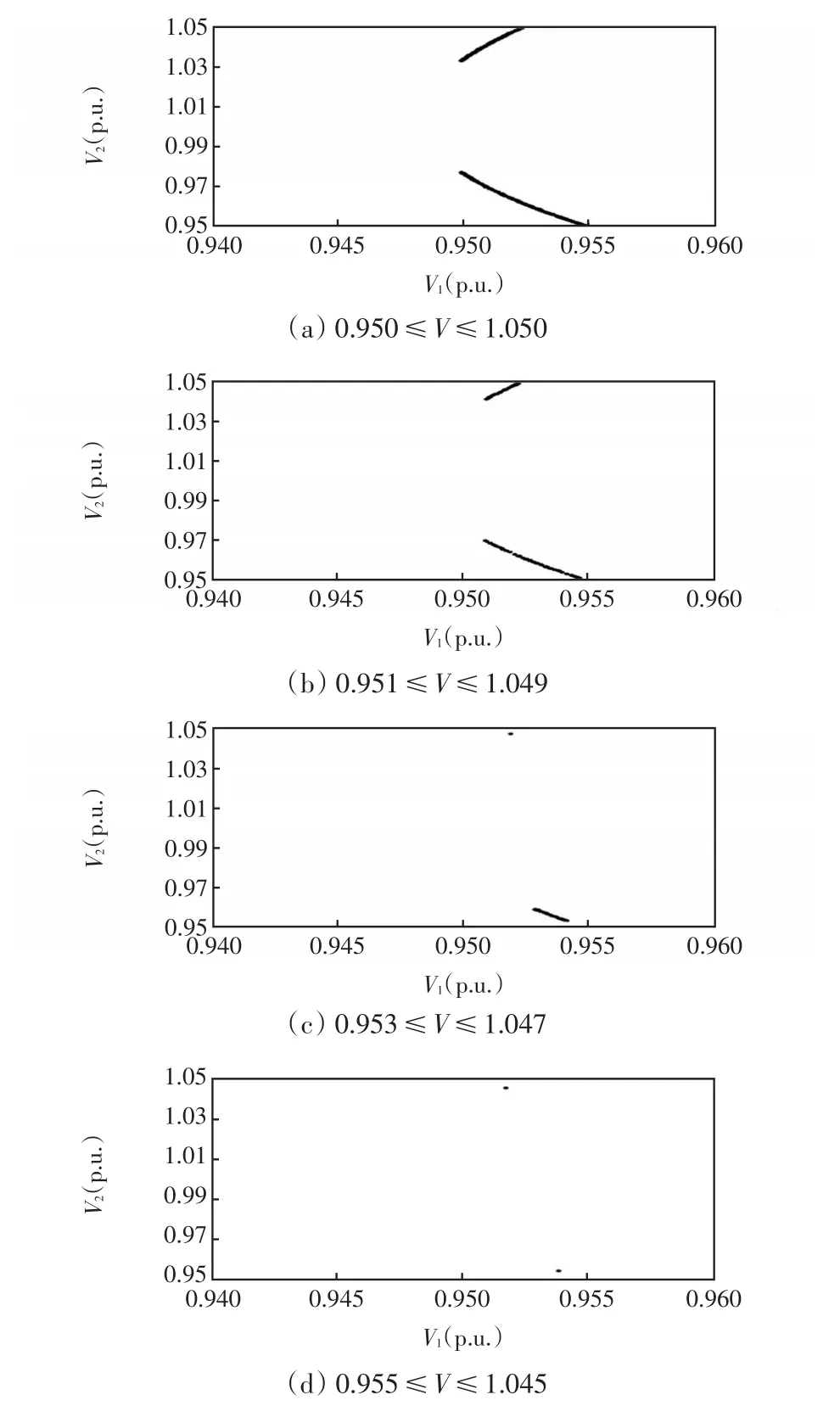
图3 2节点系统在不同电压约束下稳定平衡流形的变化情况Fig.3 Variation of stable equilibrium manifolds of a 2-bus system under different voltage constraints

4.2.2 线路潮流约束

对于第3节提到的9节点系统，在本节中，将分如下两种情况进行讨论。

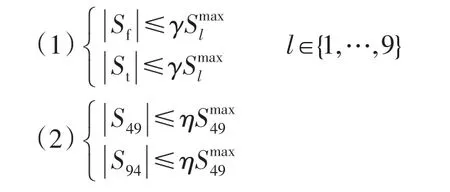
式中，γ和η分别为表征所有线路和线路4-9潮流上限变化的参数。

在第1种情况下，所有线路潮流的上限将同时并以相同的比例收紧，而在第2种情况下，仅收紧线路4-9的潮流上限。如图4所示，由于线路潮流约束是非线性的，它们对可行域的影响也是非线性的。

图4 9节点系统在不同线路潮流约束下稳定平衡流形的变化情况Fig.4 Variation of stable equilibrium manifolds of a 9-bus system under different branch flow limits

4.3 不同负荷条件对可行域的影响

为了研究系统运行在不同负荷条件下可行域将如何变化，在式（1）中加入了负荷条件参数λ，则有

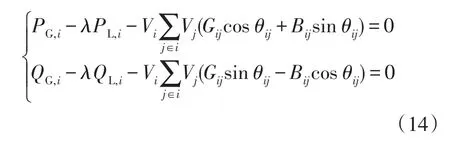
在下面的2节点系统测试中，将研究可行域和负荷条件参数之间的关系。从图5可以看出，当λ从1.00变化到1.01时，两个原不连通的稳定平衡流形将合并成一个连通的稳定平衡流形并且变大。这个测试结果表明，当负荷条件变化时（如从1.01变为1.00），最优潮流问题可能出现多个不连通的可行部分。然后，随着λ继续增加，稳定平衡流形将平移并进一步增大。当λ大约为1.10时，稳定平衡流形开始变小（这解释了为什么当负荷很重时最优潮流问题很难计算），当λ大约为1.22时，只剩下退化稳定平衡流形，这意味着此时最优潮流问题是不可行的。

图5 2节点系统在不同负荷条件参数下稳定平衡流形的变化情况Fig.5 Variation of stable equilibrium manifolds of a 2-bus system under different loading conditions

第4.2节和第4.3节中的算例结果表明，在不同的系统参数下，可行域的形状和大小会改变。可行域通常在中等负荷条件下更大，这部分解释了为什么当负荷非常轻或极重时最优潮流问题难以解决。在一些极端条件下，可行域可能消失（即最优潮流问题是不可行的）。此外，对于一些特定参数，原不连通的可行部分可能会合并成一个连通的可行域，这种现象部分解释了最优潮流问题中多个可行部分和不同的局部最优解存在的原因。

5 结 语

本文对非线性最优潮流问题的可行域进行了完整的刻画。这种刻画是通过构造与非线性最优潮流问题的等式约束以及不等式约束相关的非双曲动力学系统—商梯度系统来完成的。接下来，利用稳定平衡流形对可行域进行了可视化，并且数值验证了文中的定理。此外，本文将稳定平衡流形进一步应用于研究在特定条件下可行域将如何发生变化。在第4.2节和第4.3节中，对所有类型的约束，包括线性框式约束、非线性线路潮流约束和含有负荷条件参数的等式约束都进行了数值测试。结果表明，在不同的系统参数下，可行域的形状和大小会逐渐变化，在某些极端条件下，可行域可能会消失，而且对于某些特定的参数，原来不连通的可行部分可能会合并成一个连通的区域。

[1]Carpentier J.Contribution to the economic dispatch problem[J].Bull Sac France Elect，1962，3（4）：836-845.

[2]张德举，郭力，王成山（Zhang Deju，Guo Li，Wang Chengshan）.高风电渗透率下的独立型微网优化调度方法（Optimal dispatching method of isolated microgrids with high wind power penetration rate）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2016，28（9）：1-7，13.

[3]Pandya K S，Joshi S K.A survey of optimal power flow methods[J].Journal of Applied Information Technology，2005，4（5）：450-458.

[4]Schecter A，O’Neill R P.Exploration of the ACOPF feasible region for the standard IEEE test set[EB/OL].https：//www.ferc.gov/industries/electric/indus-act/market-planning/opfpapers/acopf-6-test-problem-properties.pdf，2013.

[5]Zhang Baosen，Tse David.Geometry of injection regions of power networks[J].IEEE Trans on Power Systems，2013，28（2）：788-797.

[6]Hnyilicza E，Lee S T Y，Schweppe F C.Steady-state security regions：Set-theoretic approach[C]//PICA Conference.New Orleans，USA，1975：347-355.

[7]Wu F F，Kumagai S.Steady-state security regions of power systems[J].IEEE Trans on Circuits and Systems，1982，29（11）：703-711.

[8]余贻鑫（Yu Yixin）.电力系统安全域方法研究述评（Review of study on methodology of security regions of power system）[J].天津大学学报（Journal of Tianjin University），2008，41（6）：635-646.

[9]王成山，许晓菲，余贻鑫，等（Wang Chengshan，Xu Xiaofei，Yu Yixin，et al）.电力系统电压稳定域的局部可视化描述及其应用（Visualization of part of the static voltage stability region in power systems and its application）[J].中国电机工程学报（Proceedings of the CSEE），2004，24（3）：1-5.

[10]曾沅，余贻鑫（Zeng Yuan，Yu Yixin）.电力系统动态安全域的实用解法（A practical direct method for determining dynamic security regions of electrical power systems）[J].中国电机工程学报（Proceedings of the CSEE），2003，23（5）：24-28.

[11]曾沅，樊纪超，余贻鑫，等（Zeng Yuan，Fan Jichao，Yu Yixin，et al）.电力大系统实用动态安全域（Practical dynamic security regions of bulk power systems）[J].电力系统自动化（Automation of Electric Power Systems），2001，25（16）：6-10.

[12]Alves D A，de Costa G R M.An analytical solution to the optimal power flow[J].IEEE Power Engineering Review，2002，22（3）：49-51.

[13]Chiang H D，Jiang C Y.Feasible region of optimal power flow：Characterization and applications[J].IEEE Trans on Power Systems，DOI：10.1109/TPWRS.2017.2692268.

[14]Bukhsh W A，Grothey A，Mckinnon K I M，et al.Local solutions of the optimal power flow problem[J].IEEE Trans on Power Systems，2013，28（4）：4780-4788.

Characterization of Feasible Region for Optimal Power Flow Problem Based on Dynamical System

JIANG Chuyang1，CHIANG Hsiao-Dong2
（1.School of Electrical and Information Engineering，Tianjin University，Tianjin 300072，China；2.School of Electrical and Computer Engineering，Cornell University，Ithaca 14853，USA）

Feasible region is fundamental and important for the optimal power flow（OPF）problem.Because of the existence of nonlinear constraints，the feasible region of OPF problem is usually complex.In this paper，a non-hyperbolic dynamical system is proposed and its stable equilibrium manifolds will be used to completely characterize the feasible region of OPF problem.Meanwhile，the validity of the proposed method is verified by theoretical and numerical analysis.In the end，the stable equilibrium manifolds of the dynamical system are applied to visualize the feasible region of the OPF problem，and further analyze the variations of feasible region with different constraint parameters.

optimal power flow（OPF）；feasible region；dynamical system；stable equilibrium manifold

TM711

A

1003-8930（2017）10-0012-06

10.3969/j.issn.1003-8930.2017.10.003

2017-05-23；

2017-07-19

国家自然科学基金重点资助项目（51337007）

江出阳（1987—），男，博士研究生，研究方向为优化方法、动力学系统及其在电力系统中的应用。Email：justpayne@tju.edu.cn

江晓东（1956—），男，博士，教授，博士生导师，研究方向为电力系统稳定和控制、非线性系统理论及其应用、全局优化技术和应用。Email：chiang@ece.cornell.edu