一种分数维改进的长方棋盘覆盖算法

王海燕，黄 骏

(1.宿迁学院信息工程学院，江苏 宿迁 223800； 2.南方科技大学计算机科学与技术系，广东 深圳 518055)

一种分数维改进的长方棋盘覆盖算法

王海燕1，黄 骏2

(1.宿迁学院信息工程学院，江苏 宿迁 223800； 2.南方科技大学计算机科学与技术系，广东 深圳 518055)

基于含有一个特殊方格的ik×jk棋盘结构，提出了一种改进与推广的长方棋盘覆盖算法。利用类似L型骨牌总是可以覆盖其余不含特殊方格子棋盘的顶点交汇处这一特点，对不含特殊方格的子棋盘算法进行改进，采用直接+间接递归及分治策略思想，以i=j=2为例设计了4个模块函数。该算法不仅避免了非特殊方格递归求解的盲目性，也减少了棋盘深层递归的层数。实验结果表明：与已有算法相比，改进的算法具有更好的性能。更加便于任意形状图像加密过程中所需的行与列不相等的二维随机密钥的生成。

棋盘覆盖；分治策略；直接递归；间接递归；图像加密

0 引言

棋盘问题是一个经典问题，早在1848年的时候，德国象棋大师马克思就提出解决8个女皇的棋盘覆盖难题的第一套方案，德国数学家高斯先生把8个女皇的棋盘覆盖推广到了n个女皇。到了1946年的时候，美国哲学家马克思又提出了二缺格国际象棋棋盘的类似围棋棋盘的双格骨牌填充方法的难题，掀起了第二次棋盘覆盖的研究热潮，1973年的时候，这个难题被美国数学家Gomory一举解决，到了20世纪80年代，基于四格骨牌的俄罗斯方块的游戏由此产生，今天类似的算法已经被广泛应用于数学领域[1-4]及计算机领域的文件加密[5]、图像加密[6-7]等技术处理中。冯跃峰[8]在数学上对中外棋盘覆盖问题进行了系统的总结阐述，给出的棋盘定义：所谓m×n棋盘是指由m行n列方格构成的m×n矩形，简称棋盘，每个方格称为棋盘的格，在一个ik×jk个方格组成的棋盘中，如有一个方格与其他方格不同，比如已经被填上代表棋子的字母、数字、符号或颜色，则称该方格为特殊方格；在计算机上解决棋盘覆盖问题使用分治策略，分治策略思想是分而治之，把一个复杂的问题分成多个相同或相似的子问题，再把子问题继续划分为更小的子问题，直到可以简单求得最小问题，原问题的解即是子问题解的合并。采用该策略给出棋盘覆盖的计算机实现方法[9]：用L型骨牌覆盖给定的棋盘上除特殊方格以外的所有方格，但是该算法没有考虑L型骨牌覆盖棋盘的特殊性，致使算法性能下降。

本文提出了一种直接+间接递归及分治策略相结合的算法，可以改进非特殊方格的棋盘算法性能。当行数与列数不是2的倍数，又不相等的时候，我们利用分数维自相似的概念，将类似L型骨牌打碎，填补到i行j列的子棋盘的顶点交汇处。在分形几何中，分数维D(即分形维数)是一个描述一个分形对空间填充程度的统计量。分数维的定义根据运用场景的精细程度有几个变种，主要的分数维定义方法是豪斯多夫维数、计盒维数和分配维数等。在分形几何中，计盒维数也称为盒维数、闵可夫斯基维数，是一种测量距离空间，特别是豪斯多夫空间，比如欧氏空间中分形维数的常用计算方法。要计算分形的维数，可以想象把这个分形放在一个均匀分割的网格上，数一数最小需要几个格子来覆盖这个分形。通过对网格的逐步精化，查看所需覆盖数目的变化，从而计算出计盒维数。换一个角度看，分形就好比是一个破碎的整形空间，在整形中看到的破碎骨牌，在分形中看到的可能就是一个完整的骨牌。它表征分形在通常的几何变换下具有不变性，即标度无关性。自相似性是从不同尺度的对称出发，也就意味着递归。线性分形又称为自相似分形。自相似原则和迭代生成原则是分形理论的重要原则。标准的自相似分形是数学上的抽象，迭代生成无限精细的结构，如科契雪花曲线、谢尔宾斯基地毯等。

当i=j=2时，棋盘类似象棋或围棋棋盘；象棋棋盘的覆盖问题游戏规则种类繁多，围棋棋盘的覆盖问题规则相对简单一点，但是排列组合远远超过象棋棋盘，谷歌的深度学习算法战胜了韩国围棋大师，说明了人工智能算法已经在正方形的二维图像处理上有了突破性的进展。当i=j=3时，棋盘类似中国古代的九宫图。当我们利用这类算法对二维图像进行加密的时候，会发现所有的图像格式其实都不是像棋盘那样的正方形，而是3∶2，4∶3或者16∶9等等的长方形，因此有必要把算法推广到像素的行与列不相等的情形，以便快速地处理实时的视频电影信息等等。正方形是长方形的特例，适合于正方形的算法不一定合适长方形，相反适合于长方形的算法不一定合适正方形，所以我们需要在正方形的基础上对长方形棋盘做了一些开拓性的初步研究。基本思路就是把大L骨牌横向和(或)纵向打碎，适应长方形的形状。

1 算法研究

采用分治策略可将棋盘划分为如图1所示的4个2(k-1)×2(k-1)个子棋盘，特殊方格必位于较小子棋盘之某个方格中。图2所示为L型骨牌的4种不同的存在形式，使其覆盖不含特殊方格的3个子棋盘交汇处，如图3所示。未被L型骨牌覆盖的方格就成了含特殊方格的更小规模子棋盘。

图1 2k×2k棋盘(k=3)

图2 4种不同形态的L型骨牌

图3 L型骨牌覆盖非特殊方格的子棋盘交汇处

经典的棋盘覆盖算法是将规模2k×2k的棋盘划分为4个子棋盘，进而对任一个子棋盘覆盖问题采用直接递归调用，而没有考虑L型骨牌覆盖棋盘时，总是覆盖不含特殊方格的子棋盘交汇处的这一特点，改进的算法充分考虑了这一特性。

为了叙述方便，把特殊方格分为两类：一类是已知条件的特殊方格，该特殊方格是随机放置，称为Irregular方格棋盘，图3所示的子棋盘4称为Irregular方格棋盘；另一类是通过L型骨牌覆盖而形成规则方格的子棋盘，称为Regular方格棋盘，图3所示的子棋盘1、子棋盘2、子棋盘3均为Regular方格棋盘。含有Irregular方格的子棋盘直接递归调用，而对于Regular方格的棋盘，则应采用直接+间接递归并用的调用方式。

根据L型骨牌覆盖子棋盘的位置，可将Regular方格棋盘分为4类情况：第1种情况，通过L型骨牌覆盖的位置在子棋盘左上角，如图4(a)所示，记作LTChessBoard棋盘；第2种情况，通过L型骨牌覆盖的位置在子棋盘左下角，如图4(b)所示，记作LBChessBoard棋盘；第3种情况，通过L型骨牌覆盖的位置在子棋盘右上角，如图4(c)所示，记作RTChessBoard棋盘；第4种情况，通过L型骨牌覆盖的位置在子棋盘右下角，如图4(d)所示，记作RBChessBoard棋盘。

图4 4种Regular方格棋盘

2 各模块算法设计

棋盘可以用一个二维数组表示board，二维数组大小2k×2k；用L型骨牌覆盖含特殊方格的2k×2k棋盘，容易得出需要L型骨牌的个数为(4k-1)/3个，将所有L型骨牌从1开始编号，则问题可以转化为用整形title变量值覆盖棋盘方格。为了递归处理的过程使用同一个棋盘、同一个变量覆盖，将二维数组和title变量设计为全局量。

2.1 主模块算法设计

用dr，dc表示特殊方格的行标和列标，则特殊方格可以用board[dr][dc]表示。不同用户或同一用户输入特殊方格的位置没有具体要求，因此特殊方格的位置可以是2k×2k棋盘中的任一方格且无规律，因此主模块首先调用的算法是Irregular棋盘算法。

2.2 Irregular棋盘算法设计

任一子棋盘可由左上角的位置(tr，tc)及棋盘面积s表示，初始的Irregular棋盘被递归划分为4个子棋盘，分别是子棋盘1、子棋盘2、子棋盘3、子棋盘4，如图1所示。

把含有用户任意输入的特殊方格棋盘采用直接递归的调用；其余子棋盘采用直接+间接递归调用，即根据L型骨牌覆盖子棋盘的位置不同，调用对应的算法。根据用户输入的特殊方格的位置，将Irregular棋盘算法也分为4种情况：第1种情况：用户输入的特殊方格位于子棋盘1中，子棋盘1采用直接递归调用算法，子棋盘2、3、4用L型骨牌覆盖交汇处，并分别调用LBChessBoard、RTChessBoard、LTChessBoard棋盘算法；第2种情况：用户输入的特殊方格位于子棋盘2中，棋盘2采用直接递归调用算法，棋盘1、3、4用L型骨牌覆盖交汇处，并分别调用RBChessBoard、RTChessBoard、LTChessBoard棋盘算法；第3种情况：用户输入的特殊方格位于子棋盘3中，棋盘3采用直接递归调用算法，棋盘1、2、4用L型骨牌覆盖交汇处，并分别调用RBChessBoard、LBChessBoard、LTChessBoard棋盘算法；第4种情况：用户输入的特殊方格位于子棋盘4中，棋盘4采用直接递归调用算法，棋盘1、2、3用L型骨牌覆盖交汇处，并分别调用RBChessBoard、LBChessBoard、RTChessBoard棋盘算法。

2.3 Regular棋盘算法设计

2.3.1 RBChessBoard棋盘

递归划分RBChessBoard子棋盘为4个更小子棋盘，即划分为子棋盘1-1、1-2、1-3、1-4 4个子棋盘，如图5(a)所示。特殊方格一定在子棋盘1-4的左下角，故直接递归调用RBChessBoard棋盘算法，L型骨牌覆盖子棋盘1-1、1-2、1-3。子棋盘1-1直接递归调用RBChessBoard棋盘算法，子棋盘1-2、1-3分别调用LBChessBoard、RTChessBoard棋盘算法。

2.3.2 LBChessBoard棋盘

递归划分LBChessBoard子棋盘为4个更小子棋盘，即划分为子棋盘2-1、2-2、2-3、2-4 4个子棋盘，如图5(b)所示。特殊方格一定在子棋盘2-3的左下角，故直接递归调用LBChessBoard棋盘算法，L型骨牌覆盖子棋盘2-1、2-2、2-3。子棋盘2-2直接递归调用LBChessBoard棋盘算法，子棋盘2-1、2-4分别调用RBChessBoard、LTChessBoard棋盘算法。

2.3.3 RTChessBoard棋盘

递归划分RTChessBoard子棋盘为4个更小子棋盘，即划分为子棋盘3-1、3-2、3-3、3-4 4个子棋盘，如图5(c)。特殊方格一定在子棋盘3-2的右上角，故直接递归调用RTChessBoard算法，L型骨牌覆盖子棋盘3-1、3-2、3-3。子棋盘3-3直接递归调用RTChessBoard棋盘算法，子棋盘3-1、3-4分别调用RBChessBoard、LTChessBoard棋盘算法。

2.3.4 LTChessBoard棋盘

递归划分LTChessBoard子棋盘为4个更小子棋盘，即划分为子棋盘4-1、4-2、4-3、4-4 4个子棋盘，如图5(d)所示。特殊方格一定在子棋盘LT1-1的左上角，故直接递归调用LTChessBoard棋盘算法，L型骨牌覆盖子棋盘4-1、4-2、4-3。子棋盘4-4直接递归调用LTChessBoard棋盘算法，子棋盘4-2、4-3分别调用LRBChessBoard、RTChessBoard棋盘算法。

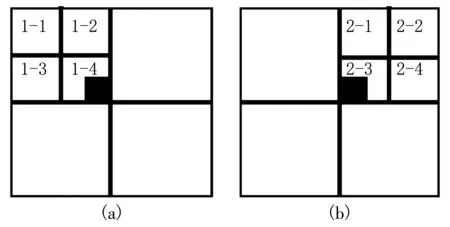
图5 4个子棋盘划分为更小的棋盘

3 算法性能分析

为了分析改进后的算法和传统算法执行时间的优劣，表1给出传统棋盘覆盖算法的运行时间复杂度和改进后棋盘覆盖算法运行时间复杂度。可以看出两类算法在k=0与k>0时，算法时间复杂度趋于相等，但由于算法时间复杂度是一个渐近值，考察这两类算法性能的优劣是不足够的。

表1 不同算法时间复杂度比较

对表1的每一项分析可知：

1)当k=0时棋盘只有一个棋格，两类算法没有任何区别；

2)当k>0时，考察算法的性能主要由3个部分组成：测试特殊方格、覆盖子棋盘及覆盖子棋盘需4次递归调用，其中覆盖子棋盘与覆盖子棋盘调用次数二者没有区别。而传统算法由于没有考虑覆盖子棋盘的特殊性，致使程序不断在子棋盘中测试特殊方格，测试次数也随着棋盘的不断划分而不断的增大；改进后的棋盘算法由于考虑了L型骨牌覆盖的特殊性，因此在特殊方格测试上，只有初始状态1次测试，通过L型骨牌覆盖的子棋盘则无需再测试，因此测试特殊方格的次数不会随着棋盘的不断划分而增大，测试次数见表2。

表2 不同算法测试特殊方格的次数对比

4 算法推广与应用

在一个ik×jk个方格组成的棋盘中，本算法依然可以利用类似L型骨牌覆盖位置的特殊性，这个时候母棋盘是m=ik行与n=jk列，子棋盘有i×j个，利用分数维的概念，我们把类似L型的大骨牌打碎成L型与O型(方形四格骨牌)或其他形状的骨牌，然后覆盖到子棋盘的每个顶点交叉的位置，把特殊方格安排在子棋盘的靠母棋盘重心均匀分布的子棋盘顶角上，进而对有规律的子棋盘设计相应的算法。

当i=j=2时，我们用Xn表示第t次划分子棋盘的总共覆盖次数，则有以下的递推公式：

Xt+1=Xt+(22-1)Xt，X0=1；

当i=j不一定一样大小时，覆盖骨牌的种类就会多于一种，则有以下的递推公式：

Xt+1=Xt+(i×j-1)Xt，X0=1。

图6显示了棋盘覆盖算法用于图像处理中。图6的左面是原图像，右面则是对原图像加密后的图像。

图6 用棋盘覆盖算法加密图像效果

5 结语

与传统的算法比较，分数维改进算法充分考虑了L型骨牌覆盖棋盘的规律性，采用直接+间接递归及分治策略完成了长方(包含正方形)棋盘所有方格的覆盖，运行效率得到了改善，运行结果工整且对称，便于快速生成二维图像的加密秘钥。

本文在阐述棋盘覆盖问题的数学形式基础上，找出了现有算法存在的不足，提出了改进棋盘覆盖算法的各模块设计与实现方法，下一步工作重点是将改进的算法用在实时图像等技术领域。

[1] Mitchell A.A block decomposition algorithm for computing rook polynomials[EB/OL].(2017-07-28).http：//arxiv.org/PS_cache/math/pdf/0407/0407004.pdf.

[2] 郭燕莎，张大坤.棋盘多项式非递归生成算法的提出与实现[J].计算机科学与探索，2007，1(2)：200-206.

[3] 牛立新，王功明，李洪淇，等.棋阵多项式生成算法及其在禁位排列中的应用[J].计算机工程与应用，2006，42(10)：91-93.

[4] 吴文虎，王建德.组合数学的算法与程序设计[M].北京：清华大学出版社，1998.

[5] xiaoge.基于棋盘覆盖的文件加密方法[J/OL].[ 2013-09-11](2017-07-28).http：//www.jiamisoft.com/blog/6288-weiyunsuantuxiangjiamifangfa.html.

[6] 杜俊利，张景飞，黄心汉.基于视觉的象棋棋盘识别[J].计算机工程与应用，2007，43(34)：220-222.

[7] Stuart Bennett，Joan Lasenby.Chess-quick and robust detection of chess-board features[J].Computer Vision and Image Understanding，2014(18)：197-210.

[8] 冯跃峰.棋盘上的组合数学[M].上海：上海教育出版社，1998.

[9] 王晓东.计算算法设计与分析[M].北京：电子工业出版社.2006

AFractionalImprovedDimensionalRectangularChessboardCoveringAlgorithm

WANG Hai-yan，et al.

(SchoolofComputerEngineering，SuqianCollege，SuqianJiangsu223800，China)

An improved and spread rectangular chessboard covering algorithm has been proposed based on a chessboard structure that included a special gridik×jk.By using the characteristics that the L domino always covers the intersection of sub-board without special grid，the algorithm to chessboard without special grid has been improved.Four modules functions are designed by adopting the combination idea of direct and indirect recursion and dividing-conquering strategy，takingi=j=2 as example.This algorithm can not only avoid the blindness of recursion solution to the sub-board without special grid，but also reduce the number of layers on recursion.The experimental results show that compared with the existing algorithms，this improved algorithm has better performance，which is more convenient for the generation of two-dimensional random keys that do not have the same row and column in the arbitrary shape image encryption process.

chessboard cover；divide and conquer strategy；directly recursive；indirect recursive；video encryption

10.3969/j.issn.1009-8984.2017.03.028

2017-08-02

江苏省大学生创新创业训练计划项目(201614160034H)宿迁学院教学改革研究项目(sqc2016jg10)

王海燕(1975-)，女(汉)，副教授，硕士 主要研究软件工程，数据挖掘。

TP3

A

1009-8984(2017)03-0119-05