基于信息熵与计量经济学模型的饱和负荷预测方法

赵 栩

(长春工程学院电气与信息学院，长春 130012)

基于信息熵与计量经济学模型的饱和负荷预测方法

赵 栩

(长春工程学院电气与信息学院，长春 130012)

对于长期的负荷预测来说，采用单一的预测模型进行远景年饱和预测时显然是不够的，为了充分利用每种单一预测模型的优点，提出基于信息熵与计量经济学模型的饱和负荷预测方法。首先选用计量经济学模型分别预测了全社会用电量的饱和值、三产计算用电量的饱和值以及人均用电量的饱和值，并通过上述3种途径分别预测出全社会用电量的饱和值，然后计算上述3种方法预测偏离误差的熵值，并确定每种方法的权重，建立最终的组合预测模型，并用实例分析验证了所提方法的有效性。

饱和负荷；熵权法；计量经济学模型；组合预测模型

0 引言

随着城市发展规模的逐渐稳定，城市电网负荷的发展也趋于饱和，饱和负荷预测也成为近年来电网规划中的热门话题，建立合理的饱和负荷预测模型是急需的。现有的饱和预测模型大多为人均用电量法[1]、计量经济学模型[2-3]、系统动力学模型[4]和生长曲线模型[5]，为了充分挖掘各单一预测模型的优点，本文首先基于计量经济学模型分别预测了全社会用电量的饱和值、三产用电量的饱和值以及人均用电量的饱和值，并分别通过上述3种途径分别预测出全社会用电量的饱和值，再计算上述3种途径预测偏离误差熵值后，确定每种方法的权重，建立最终的组合预测模型，并用实例分析验证了所提方法的有效性。

1 熵权的基本原理

通过确定每种方法预测值的无序程度，来判断每种预测方法与实际值之间的偏离程度，从而确定每种方法在组合法中的权重。如果确定的熵值越大，那么说明该方法的预测结果越偏离实际值，在组合预测模型中占的比重越小。每种预测方法熵值的确定如式(1)：

(1)

式中：eit为第i种方法第t年的相对误差；T为时间序列的长度，t=1，2，…，T。

根据每种方法预测结果的熵值，确定每种方法在组合预测模型中的权重，如式(2)：

(2)

最终利用熵权组合法确定目标年的负荷值，如式(3)：

Qt=λiQit，

(3)

式中Qit为第i种方法第t年的电量预测值。

2 计量经济学模型的原理

计量经济学模型的一般表达式如式(4)：

y=f(x，a，μ)，

(4)

式中：y与x为模型变量；a为模型系数；μ为随机误差项。

对于上述模型，本文选取与负荷值相关性较高的影响因素作为模型中的自变量，其中与用电负荷相关性较高的因素包括社会发展的经济、社会总人口和城市的平均温度等，但是上述因素中易于获取并可预测其饱和值的因素只有社会经济GDP和社会总人口POP，所以本文建立以GDP和POP为变量的计量经济学模型。只需预测出GDP与POP的饱和值，就可以从多种预测途径出发预测全社会总用电量的饱和值。下面介绍利用计量经济学模型预测全社会用电量饱和值的多种途径：

1)全社会用电量预测模型，见式(5)：

Q=a1+a2GDP+a3POP+μ1，

(5)

式中：Q为预测区内全社会用电总量；a1、a2、a3为常数；GDP为预测区国民生产总值；POP为预测区内的社会总人口；u1为随机扰动项。

2)人均用电量预测模型，见公式(6)：

Q1=a4+a5GDP+a6POP+μ2，

(6)

式中：Q1为预测区内年人均用电量；a4、a5、a6为常数；u2为随机扰动项。

根据预测出的人均用电量，求出全社会用电量，见公式(7)：

Q=POP×Q1。

(7)

3)建立各行业用电量的计量经济学模型：

建立第一产业用电量的预测模型：

Q2=a7+a8GDP+a9POP+μ3，

(8)

式中：Q2为预测区内第一产业年用电量；a7、a8、a9为常数；u3为随机扰动项。

建立第二产业用电量的预测模型：

Q3=a10+a11GDP+a12POP+μ4，

(9)

式中：Q3为预测区内第二产业年用电量；a10、a11、a12为常数；u4为随机扰动项。

建立第三产业用电量的预测模型：

Q4=a13+a14GDP+a15POP+μ5，

(10)

式中：Q4为规划区第三产业年度用电量；a13、a14、a15为常数；u5为随机扰动项。

建立居民类生活用电预测模型：

Q5=a16+a17GDP+a18POP+μ6，

(11)

式中：Q5为规划区年度居民生活用电量；a16、a17、a18为常数；u6为随机扰动项。

各产业用电量与全社会用电量之间的关系如式(13)：

Q=Q2+Q3+Q4+Q5，

(12)

式中：Q2为第一产业用电量；Q3为第二产业用电量；Q4为第三产业用电量；Q5为居民类负荷的用电量。

3 组合预测模型的建立

首先，用第2节中介绍的计量经济学模型，分别对全社会用电量、人均用电量和各行业用电量进行预测，然后利用第1节中的熵权法，确定各单一预测模型在组合预测模型中的权重系数，最后运用熵权组合法对目标年全社会用电量进行预测。

Qt=λ1Q1t+λ2Q2t+λ3Q3t，

(13)

式中：Qt表示第t年用电量；Qit为第i种方法第t年的电量预测值。

4 实例分析

本文选用郑州市2005年—2014年的全市年用电量为基本数据，并在统计网上收集了郑州市GDP与POP的历史值，并用生长曲线法对人口与经济的发展趋势进行分析，得到全市经济进入到饱和阶段时，所能达到的饱和值为16 084.9亿元，如图1所示。用相同的方法对郑州市区人口数量进行分析，达到饱和时人口数量约为550万人。

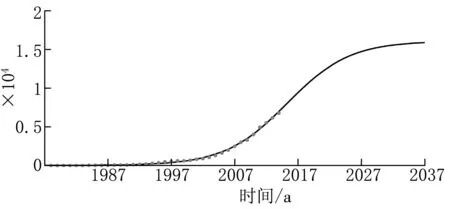
图1 生产总值GDP的发展趋势示意图

采用第2节中介绍的单一预测模型分别对全社会总用电量进行饱和值预测，预测结果及各单一预测模型的权重系数见表1。

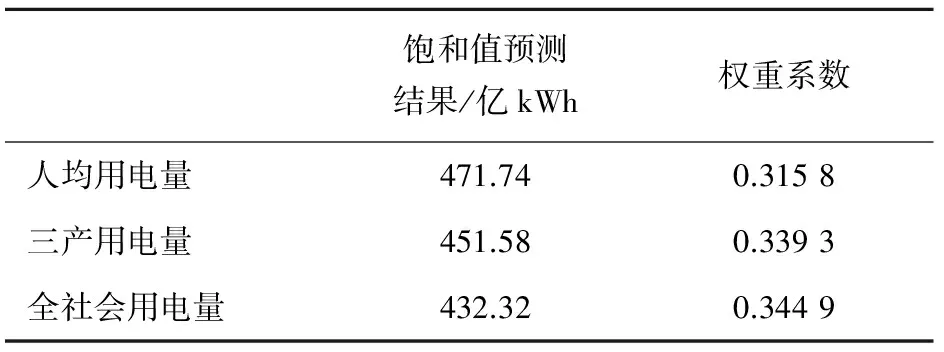
表1 各单一预测模型饱和值预测结果

每种预测模型每年详细的预测结果、每种方法的最终饱和值预测结果见表2，各模型的相对误差见表3。图2中给出了各个预测模型相对的误差波动，从图中可以明显看出组合预测模型减小了相对的误差的波动，可以更好地发挥出每种单一预测模型的优点，可以提高饱和预测结果的精度，同时验证了本文提出方法的有效性。

表2 各预测模型预测结果

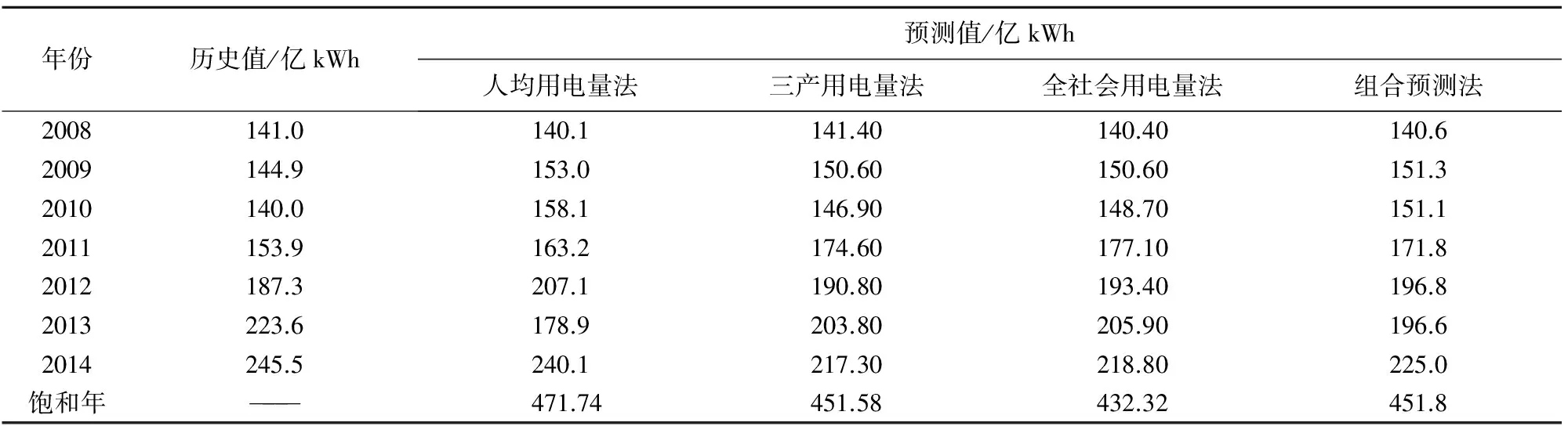
表2(续)

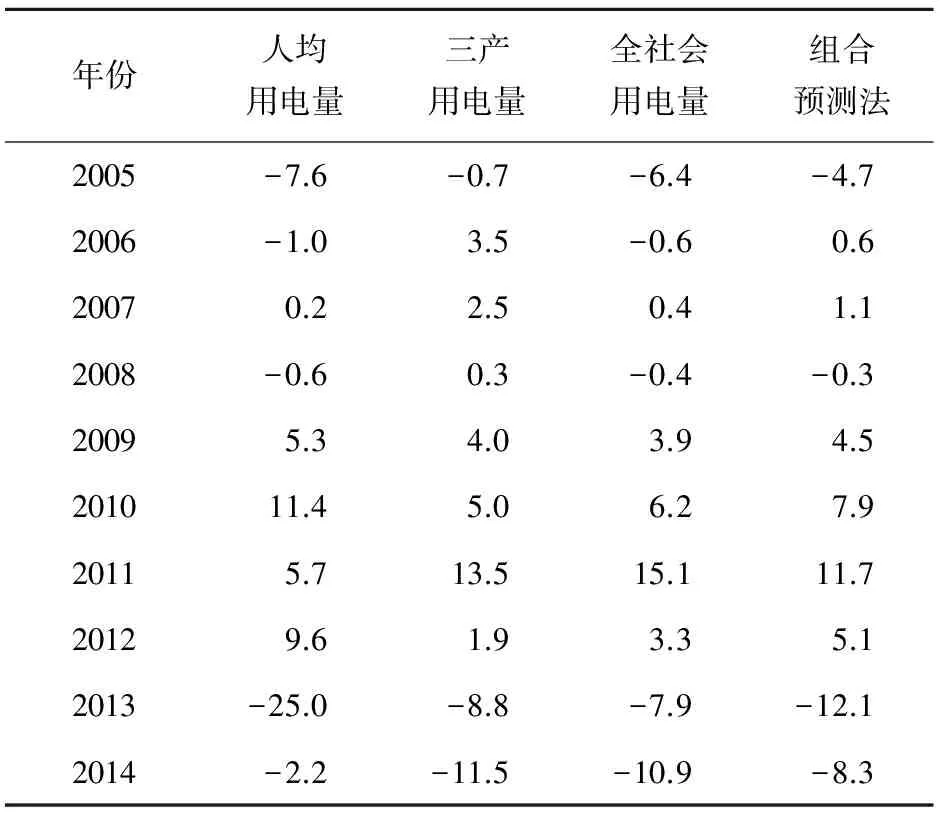
表3 各预测模型预测相对误差/%

5 结语

本文选用计量经济学模型作为基本的预测模型，并利用熵权法确定了组合预测模型中各单一预测模型的权重，组合预测法可以利用各单一预测模型预测正负误差，有效地减小最终预测结果的误差波动幅值，并用实例分析验证了该方法的有效性。

图2 各预测模型预测相对误差示意图

[1] 王伟，房婷婷.人均用电量法在区域饱和负荷预测中的应用研究[J].电力需求侧管理，2012，20(6)：34-38.

[2] 崔凯，李敬如，赵彪，等.城市饱和负荷及其预测方法研究[J].电力技术经济，2008，20(6)：34-38.

[3] 肖峻，杜柏均，耿芳.城市电力负荷饱和分析方法[J].电力科学与技术学报，2009，24(4)：54-58.

[4] 何永秀，吴良器，戴爱英，等.基于系统动力学与计量经济模型的城市饱和负荷综合预测方法[J].电力需求侧管理，2010，12(1)：21-25.

[5] 王芳东，林韩，李传栋，等.基于经济曲线饱和态势分析的饱和负荷宏观预测研究[J].华东电力，2010，38(10)：1486-1491.

TheSaturatedLoadForecastingMethodBasedonInformationEntropyandEconometricModel

ZHAO Xu

(SchoolofElectrical&InformationEngineering，ChangchunInstituteofTechnology，Changchun130012，China)

For the long term load forecasting，it is obviously not enough to use a single prediction model to make a saturation prediction of a prospective year.In order to make full use of the advantages of each single prediction model，this paper proposes a method of forecasting saturated load based on information entropy and econometric model.First of all，the econometric model has been chosen to predict the saturation value of the total electricity consumption in the whole society，the saturation value of the three production electricity capacity，and the saturation value of the per capita electricity consumption.Through the above three ways，the saturation value of electricity consumption in the whole society has been predicted.Then，the deviation of the error entropy value got from the above three predicting methods has been calculated to determine the weight of each method.Finally，a portfolio forecasting model has been established，and the effectiveness of the proposed method has been analyzed and verified by the practical case.

saturation load；entropy weight method；econometric model；combination forecasting model

10.3969/j.issn.1009-8984.2017.03.011

2017-09-05

赵栩(1973-)，女(汉)，吉林省吉林市，副教授 主要研究电力系统及其自动化。

TP273

A

1009-8984(2017)03-0046-03