边坡动力稳定性分析的时程传递系数法

丁王飞，张春丽，张乃计

(1.重庆建筑工程职业学院，重庆 400072；2.重庆交通大学 土木工程学院，重庆 400074)

边坡动力稳定性分析的时程传递系数法

丁王飞1，2，张春丽1，张乃计2

(1.重庆建筑工程职业学院，重庆 400072；2.重庆交通大学 土木工程学院，重庆 400074)

传递系数法是边坡稳定性计算常用方法之一。水平地震力是边坡动力稳定性影响的主要因素，针对传统边坡稳定性计算的传递系数法，将地震加速度时程通过地震力形式归于传递系数法中的条块传递系数，计算传递系数时程，进而得到地震动力稳定系数时程，基于此提出了边坡动力稳定性分析的时程传递系数法。算例讨论得出，当地震加速度大于-0.2时，传递系数呈现出先减小后增加、再减小的整体趋势，反之，传递系数随条块表现为持续降低的规律；当地震加速度小于0时，加速度方向为反坡向，对边坡稳定性有利，反之，加剧边坡的危险性；随着地震加速度的递增，不同条块的传递系数不断线性增大。岩质边坡在地震力作用下破坏具有滞后性和突发性。

地震工程；时程传递系数；时程稳定系数；边坡

0 引 言

2008年5月12日，汶川发生8.0级大地震，地震触发了大量边滑坡灾害[1]。汶川地震诱发滑坡数量之多、分布之广、面密度之高、破坏之强、伤亡之多、损失之重举世罕见[2]。如规模最大的安县大光包滑坡，体积达约7～10×108m3；运动距离最大的绵竹文家沟高速远程滑坡，最大位移超过4 km；灾难最大的北川县城城西滑坡，导致1 600余人死亡；潜在危险性最大的北川唐家山滑坡堰塞湖，威胁绵阳30万人的生活安全。因此，研究边坡动力稳定性评价方法具有积极意义。

目前，许多学者对边坡动力稳定问题做了大量研究，如LING H I等[3]认为，当水平加速度较小时，可忽略竖向加速度对边坡动力稳定性的影响，当水平加速度加大时，竖向加速度对边坡抗震性能和滑移位移的影响不容忽略；R·SHUKHA等[4]认为地震动输入方式对边坡动力稳定评价的影响应当考虑，同时考虑水平和竖向加速度输入时，竖向加速度及其水平加速度的组合方式将在一定程度上增大或降低斜坡的稳定系数及滑移量；刘汉龙等[5]考虑地震对边坡的动力作用，提出了用最小平均稳定系数作为评价指标，发展了边坡地震稳定性时程分析方法；邓东平等[6]分析了直线、圆弧和任意曲线3种滑动面形式的边坡动力稳定性时程方法；孟庆筱等[7]提出采用设定地震方法对三峡库区地震边坡进行危险性评估；黄诚等[8]通过沿滑面的应力积分法和动力时程分析法，研究地震动单独作用对边坡动安全系数的影响，发现竖向地震动与水平地震动一样也对边坡抗震稳定性有显著的影响；徐红涛等[9]基于爆破振动峰值速度衰减规律和爆破振动速度或加速度时程曲线，计算出特定时刻作用在各条块上的爆破振动惯性力，并施加到各个条块上采用刚体极限平衡分析方法中的Sarma方法得到了稳定性时程曲线；刘建军等[10]针对以地震波作用中最后时刻或加速度值最大时刻的安全系数作为评价标准的问题，通过强度折减法，借助数值计算获得了地震载荷作用下安全系数时程曲线；张锋春等[11]结合某石灰石矿排土场动力边坡稳定性问题，得出在地震作用下边坡不同位置的位移和加速度时程，对边坡工程的动力分析具有参考意义；王环玲等[12]研究表明，用时程分析法计算边坡地震作用下的动力响应结果能够较真实地反映出岩石高边坡的动态特征以及地震对高边坡的扰动作用；许名标等[13]对水电站边坡开挖爆破动力时程分析表明，边坡不会产生共振现象，随着爆破规模的增大，出现明显的速度放大效应和惯性滞后效应；彭德红等[14]对边坡爆破开挖ANSYS分析得出，此次爆破的振动速度最大值超标，各种应力在坡脚底部存在应力集中现象。

依据时程法原理，将动力时程法与传递系数法有机结合，提出了边坡动力稳定性分析的时程传递系数法，将地震加速度时程通过地震力形式归于传递系数法中的条块传递系数，计算传递系数时程，进而得到地震动力稳定系数时程。研究成果可为地震灾区边坡动力稳定性评价提供理论指导和设计依据。

1 传递系数法简介

传递系数法是在1954年由我国最著名的滑坡专家徐邦栋提出的[15]，目前，已被广泛应用于滑坡、边坡的稳定性评价。传递系数法分为两种，一种是强度储备法，考虑分块和整体平衡，假定各条块的稳定系数与整体稳定系数相等，不允许条块间出现拉应力，滑动面剪切强度参数c与φ具有一定的安全储备；另一种是超载法，仅考虑整体平衡，允许条块间出现拉应力，滑动面剪切强度参数c与φ不变，计算时将滑动力乘以滑坡体的稳定系数。笔者仅介绍传递系数法中的超载法。

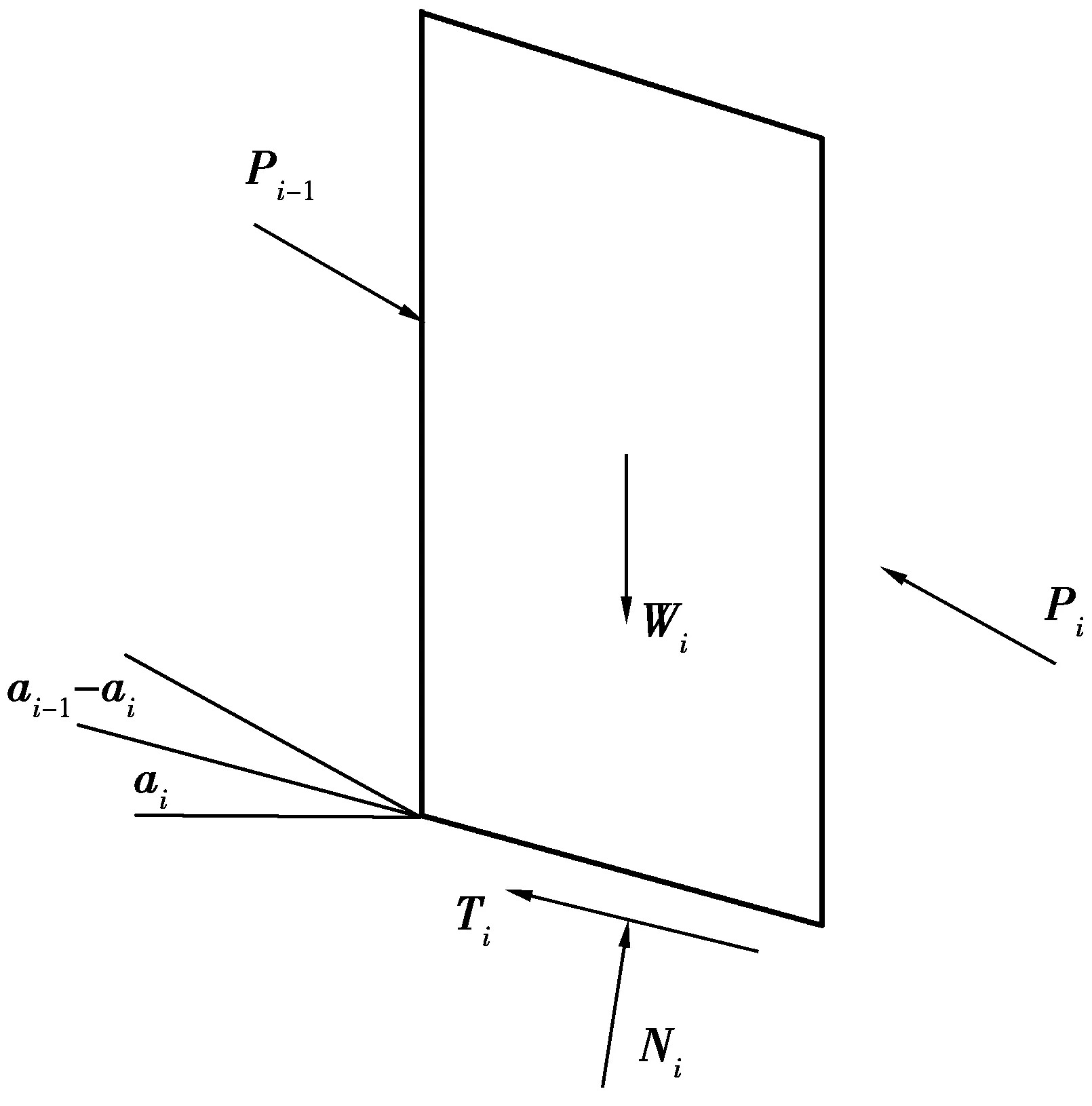
图1 条块受力分析Fig. 1 Block force analysis

如图1为传递系数法第i个条块推力计算示意图，其中，Pi-1为第i-1个条块的不平衡下滑力，方向平行于第i-1个条块的底滑面；Pi为第i个条块的不平衡下滑力，方向平行于第i个条块的底滑面；αi-1为第i-1个条块的底滑面倾角；αi为第i个条块的底滑面倾角；Wi为第i个条块重力；Ti为第i个条块底滑面抗滑力；Ni为第i个条块底滑面正压力，各参数满足平衡方程如下：

Pi=FsWisinαi-Ti+Pi-1ψi-1

(1)

其中，

Ti=cili+Wicosαitanφi

(2)

ψi-1=cos(αi-1-αi)-tanφisin(αi-1-αi)

(3)

式中：Fs为稳定系数；ψi-1为传递系数。

求解滑坡稳定系数Fs时令Pn=0，可直接得出含Fs的一次方程。

2 动力稳定性分析的时程传递系数法

2.1 加速度时程曲线

地震或爆炸产生的地震波是一种因震源或爆源剧烈运动而形成的传播于岩土体介质的弹性波，研究表明，地震波作用尤其是水平地震力是导致地震或爆炸时滑坡破坏失稳的根本动力，而水平地震力主要来源于地震力中的S波(剪切波)。如图2为一汶川水平地震加速度时程曲线，显然，加速度a随时间t不断地增强或减弱，方向也在周期性的改变。因此，加速度时程曲线可描述为

a=a(t)

(4)

式中：a(t)为水平加速度的时间函数；t为地震波作用时间。

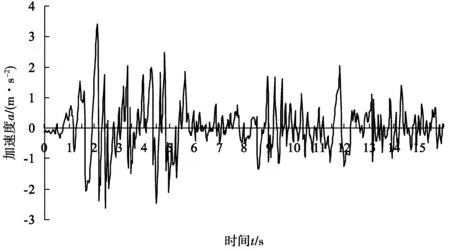
图2 汶川地震加速度时程曲线(什邡八角站记录，NS方向)Fig. 2 Time-history curve of Wenchuan seismic acceleration (recorded by Bajiao station, Shifang; NS direction)

地震波加速度对滑坡体的作用实际上是对滑体施加一等效集中惯性力，为

E=ma(t)

(5)

式中：E为地震波等效集中惯性力，作用点在滑坡体重心；m为滑坡体质量。

则在地震发生的全时域[0,t]内，地震波对滑坡体的惯性作用强弱随时间不断改变，并且直接决定了滑坡体稳定状态变化规律。

2.2 时程传递系数

将地震波产生的等效集中惯性力E作用于图1中第i个条块的重心，则此时第i个条块的受力为

WEi=mi[g+a(t)]

(6)

令η=a(t)/g，则

WEi=mig(1+η)

(7)

地震波惯性力的作用实际上是在重力的基础中增加了η倍，将地震波产生的惯性力分解到第i个条块的底滑面上，则下滑分量EiH和正压分量EiV分别为

EiH=ηmigcosαi

(8)

EiV=ηmigsinαi

(9)

式(8)与式(9)为在重力基础上增加的惯性分量，可将第i个条块产生的惯性分量等效为第i-1个条块产生的下滑力Pi-1对第i个条块的作用，而第i个条块的原始受力不变。由于Pi-1对第i个条块的作用体现在传递系数ψi-1上，传递系数ψi-1的改变实际就代表了地震波惯性分量的作用，并且，产生的惯性增量与原始受力共有mig，则地震波对滑坡体的作用在传递系数ψi-1中表达为

ψi-1=cos(αi-1-αi)+ηcosαi-tanφi[sin(αi-1-αi)+

ηsinαi]

(10)

式(10)中的传递系数ψi-1可称为时程传递系数，因为传递系数ψi-1与地震波加速度a(t)直接相关，并是时间t的变量，至此，动力对滑坡体的作用就等效为了滑坡传递系数ψi-1随时间的改变上。

采用传递系数法计算滑坡动力稳定性时，只需预先监测作用于滑坡的地震波加速度时程曲线a(t)，将其带入式(10)，得出传递系数时程曲线，并结合式(1)计算出滑坡动力稳定系数时程曲线，从滑坡动力稳定系数时程曲线得知稳定系数变化规律，进而判定滑坡动力稳定状态。

3 算例讨论

3.1 算例模型

笔者以典型的均质岩质边坡为例[16]，考虑水平向地震力对岩质边坡的地震动作用，边坡高30 m，宽30 m，坡度为1∶2(图3)。重度为2.2 kN/m3；内摩擦角为32°；黏聚力为157.5 kPa；重力加速度为9.8 m/s2。采用文中的时程传递系数法，将岩质边坡分为7个条块(表1)，将图2的汶川地震加速度时程与重力加速度求比值η，将比值η时程带入公式(10)得到传递系数时程变化曲线，进而计算岩质边坡动力稳定系数时程曲线。

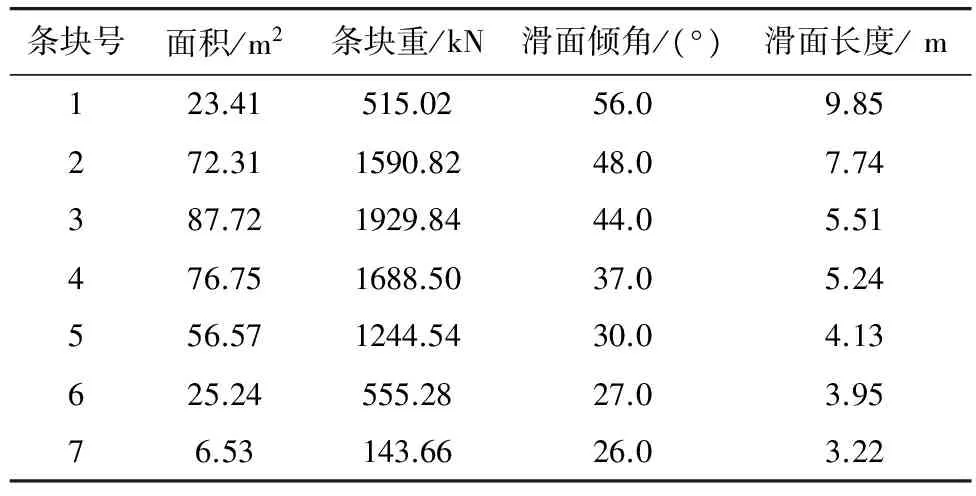
条块号面积/m2条块重/kN滑面倾角/(°)滑面长度/m123．41515．0256．09．85272．311590．8248．07．74387．721929．8444．05．51476．751688．5037．05．24556．571244．5430．04．13625．24555．2827．03．9576．53143．6626．03．22

3.2 时程传递系数变化规律

为了探求时程传递系数随地震加速度变化规律，选取-0.3、-0.2、-0.1、0(天然工况)、0.1、0.2、0.3七个地震加速度，分别计算不同条块的传递系数(图4)。图4显示以下特征：

图4 不同条块传递系数随地震加速度变化规律Fig. 4 The law of transferring coefficients of different blocks changing with the seismic acceleration

1)当地震加速度大于-0.2时，传递系数随条块呈现出先减小后增加、再减小的整体趋势，当地震加速度小于-0.2，传递系数随条块表现为持续降低的规律。

2)当地震加速度小于0时，传递系数小于天然工况下的传递系数；当地震加速度大于0时，传递系数大于天然工况下的传递系数，表明加速度方向为反坡向时，对边坡稳定性有利，反之，加剧了边坡的危险性。随着地震加速度的递增，不同条块的传递系数不断增大，地震加速度的递增梯度为0.1，图4中显示不同条块随地震加速度的增加得到的传递系数增幅基本相同，可以认为传递系数随加速度变化具有线性规律。

3.3 时程传递系数变化规律

如图5，虚线代表天然工况(地震力为0)下的稳定系数曲线，实线代表地震工况下的时程稳定系数曲线。经分析可得如下特征：

图5 岩质边坡时程稳定系数变化规律Fig. 5 Variation law of time-history stability coefficient of rock slope

1)地震工况下的时程稳定系数围绕着天然工况下的稳定系数上下波动，波动在天然工况稳定系数之上较多，占86.5%，之下较少，占13.5%，地震力具有明显增加岩质边坡稳定性的作用。

2)岩质边坡天然工况下的稳定系数为1.519，地震力作用下岩质边坡的稳定系数最大值为4.196，时刻为2.38 s，对应的加速度为1.19 m/s2，同时也是最大加速度值；最小稳定系数为1.060，时刻为5.5 s，对应的加速度为-0.027 m/s2，同时亦是最小加速度值，这与现实情况较为吻合。同时，出现的最小稳定系数的时刻为5.5 s，表明岩质边坡在地震力作用下破坏具有滞后性。

3)图5中显示，稳定系数时程曲线总体显示出规律性的15个波峰和14个波谷，波峰周期在1～1.5 s，波幅在1.5左右；波谷周期在0.5 s左右，波幅0.5左右，表明地震力对岩质边坡稳定系数增加作用集中在1.5，地震力对岩质边坡稳定系数降低作用集中在0.5。波峰左侧为稳定系数急剧上升段，右侧为相对缓慢下降段，但由于稳定系数下降周期在1～1.5 s之间，表明岩质边坡动力破坏具有突发性。

4)假定岩质边坡安全系数为1.2，图5大于1.2的稳定系数占99.23%，表明岩质边坡破坏概率为0.77%，根据边坡概率分析理论[17]，可以认为此边坡在此地震动作用下是稳定的。

4 结 语

提出了边坡动力稳定性分析的时程传递系数法，将地震加速度时程通过地震力形式归于传递系数法中的条块传递系数，计算传递系数时程，进而可得到地震动力稳定系数时程，此法计算简便，操作简单。

算例讨论得出，当地震加速度大于-0.2时，传递系数随条块呈现出先减小后增加、再减小的整体趋势，反之，传递系数随条块表现为持续降低的规律；当地震加速度小于0时，加速度方向为反坡向，对边坡稳定性有利，反之，加剧了边坡的危险性。地震工况下的时程稳定系数围绕着天然工况下的稳定系数上下波动，地震力大部分指向坡内，具有明显增加边坡稳定性的作用；而仅有小部分顺坡向地震力降低了边坡稳定性；岩质边坡在地震力作用下破坏具有滞后性。岩质边坡动力破坏具有突发性。假定岩质边坡安全系数为1.2，岩质边坡破坏概率为0.77%，根据边坡可靠度理论，此边坡在此地震动作用下是稳定的。

[1] 殷跃平. 汶川八级地震地质灾害研究[J].工程地质学报,2008,16(4):433-444.

YIN Yueping. Researches on the geo-hazards triggered by Wenchuan earthquake, Sichuan[J]JournalofEngineeringGeology, 2008, 16(4): 433-444.

[2] 吴树仁,王涛,石玲,等. 2008汶川大地震极端滑坡事件初步研究[J].工程地质学报,2010,18(2):145-159.

WU Shuren, WANG Tao, SHI Ling, et al. Study on catastrophic landslides triggered by 2008 great Wenchuan earthquake, Sichuan,China[J].JournalofEngineeringGeology,2010,18(2):145-159.

[3] LING H I, LESHCHINSKY D, MOHRI Y. Soil slopes under combined horizontal and vertical seismic accelerations[J].EarthquakeEngineeringandStructuralDynamics,2015,26(12):1231-1241.

[4]SHUKHA R, BAKER R.Design implications of the vertical pseudo-static coefficient in slope analysis[J].Computers&Geotechnics, 2008, 35(1): 86-96.

[5] 刘汉龙, 费康, 高玉峰. 边坡地震稳定性时程分析方法[J]. 岩土力学,2003,24(4):553-560.

LIU Hanlong, FEI Kang, GAO Yufeng. Time history analysis method of slope seismic stability[J].RockandSoilMechanics, 2003, 24(4): 553-560.

[6] 邓东平, 李亮, 赵炼恒. 地震作用下边坡稳定性分析的拟静力法研究[J].中南大学学报(自然科学版),2014,15(10):3578-3588.

DENG Dongping, LI Liang, ZHAO Lianheng.Research on quasi-static method of slope stability analysis during earthquake[J].JournalofCentralSouthUniversity(ScienceandTechnology), 2014, 15(10): 3578-3588.

[7] 孟庆筱, 姚运生, 胡国新, 等. 巴东黄土坡滑坡稳定性分析[J]. 大地测量与地球动力学,2012,32(6):65-70.

MENG Qingxiao,YAO Yunsheng,HU Guoxin,et al.Stability analysis of Huangtupo landslide[J].JournalofGeodesyandGeodynamics, 2012, 32(6): 65-70.

[8] 黄诚, 王安明, 任伟中. 水平向与竖向地震动的时间遇合模式对边坡动力安全系数的影响[J]. 岩土力学,2010,31(11):3404-3410.

HUANG Cheng, WANG Anming, REN Weizhong. Influence of time combination pattern of horizontal and vertical ground motions on slope seismic safety factor[J].RockandSoilMechanics, 2010, 31(11): 3404-3410.

[9] 徐红涛,卢文波,周创兵,等.基于时程分析的岩质高边坡开挖爆破动力稳定性计算方法[J].岩石力学与工程学报,2006,25(11):2213-2219.

XU Hongtao, LU Wenbo, ZHOU Chuangbing, et al. Time history analysis method for evaluating dynamic stability of high rock slope under excavation blasting[J].ChineseJournalofRockMechanicsandEngineering, 2006, 25(11): 2213-2219.

[01] 刘建军,李跃明,车爱兰.地震荷载下岩质边坡动安全系数评价[J].应用力学学报,2011,28(6):595-601.

LIU Jianjun, LI Yueming, CHE Ailan. The evaluation for dynamic safety coefficient of rock slope under seismic loading [J].ChineseJournalofAppliedMechanics, 2011, 28(6): 595-601.

[11] 张锋春, 梁力, 戴玉买. ANSYS在排土场动力时程分析中的应用[J]. 金属矿山,2009(9):160-164.

ZHANG Fengchun, LIANG Li, DAI Yumai. Application of ANSYS in the transient dynamic analysis of waste dump [J].MetalMine, 2009(9): 160-164.

[12] 王环玲, 徐卫亚. 高烈度区水电工程岩石高边坡三维地震动力响应分析[J].岩石力学与工程学报,2005,24(增2):5890-5895.

WANG Huanling, XU Weiya. 3D dynamical response analysis of high rock slope related to hydropower project in high intensive seismic region [J].ChineseJournalofRockMechanicsandEngineering, 2005, 24(Sup2): 5890-5895.

[13] 许名标, 彭德红. 某水电站边坡开挖爆破震动动力响应有限元分析[J]. 岩土工程学报,2006,28(6):770-775.

XU Mingbiao, PENG Dehong. Finite element analysis of dynamic response on blasting vibration in slope excavation of a hydroelectric power station[J].ChineseJournalofGeotechnicalEngineering, 2006, 28(6): 770-775.

[14] 彭德红. 露天矿边坡开挖爆破震动动力响应分析[J]. 煤炭学报,2005,30(6):705-709.

PENG Dehong. Analysis of dynamic response on blasting vibration about excavated slope in a surface mine[J].JournalofChinaCoalSociety, 2005, 30(6): 705-709.

[15] 沈尧亮, 侯殿英. 传递系数法的原型与衍生[J]. 工程勘察,2010(增1):477-486.

SHEN Yaoliang, HOU Dianying. Transfer coefficient method of prototype and derivatives[J].GeotechnicalInvestigation&Surveying, 2010(Sup1): 477-486.

[16] 刘红帅, 薄景山, 杨俊波. 确定岩质边坡地震安全系数的简化方法[J]. 岩石力学与工程学报,2012,31(6):1107-1114.

LIU Hongshuai, BO Jingshan, YANG Junbo. Simplified method for determining seismic safety factor of rock slope [J].ChineseJournalofRockMechanicsandEngineering, 2012, 31(6): 1107-1114.

[17] 李秀珍, 孔纪名, 李胜伟. 水电岩质边坡的稳定性概率分级方法研究[J]. 岩石力学与工程学报,2011,30(增2):4025-4032.

LI Xiuzhen, KONG Jiming,LI Shengwei. Stability probability classification method for rock slope in hydropower engineering region [J].ChineseJournalofRockMechanicsandEngineering, 2011, 30(Sup2): 4025-4032.

Time-HistoryTransferringCoefficientMethodofAnalysisonSlopeDynamicStability

DING Wangfei1,2，ZHANG Chunli1，ZHANG Naiji2

(1.Chongqing Jianzhu College,Chongqing 400072,P.R.China; 2.School of Civil Engineering,Chongqing Jiaotong University,Chongqing 400074,P.R.China)

The transferring coefficient method is one of common methods to calculate the slope stability. The horizontal seismic force is the main factor that affects the dynamic stability of the slope. Aiming at the transferring coefficient method for the traditional slope stability calculation, the time-history of seismic acceleration was classified as block transferring coefficient by seismic force in the transferring coefficient method. The time-history of transferring coefficient was calculated, and then the time-history of seismic dynamic stability coefficient was obtained. Therefore, the time-history transferring coefficient method of the analysis on the slope dynamic stability was proposed. According to the discussion on case studies, it is obtained that the transferring coefficient decreases early and increases later, and decreases again lastly when the seismic acceleration is greater than -0.2; conversely, the transferring coefficient presents the law of continuous decrease according to the block. When the seismic acceleration is less than 0, the direction of acceleration is the opposite direction of slope, which is beneficial for the slope stability; conversely, it will increase risks of the slope. With the increase of the seismic acceleration, the transferring coefficients of different blocks increase gradually and linearly. The failure of rock slope under the seismic force is lagging and sudden.

earthquake engineering; time-history transferring coefficient; time-history stability coefficient; slope

10.3969/j.issn.1674-0696.2017.11.12

2016-11-01；

2017-01-05

国家自然科学基金项目(51378520)；重庆市教委科学技术研究项目(KJ1740469)；重庆市高等教育教学改革研究项目(153296)

丁王飞(1984—)，男，安徽铜陵人，讲师，博士，主要从事道路岩土病害机理及控制方面的研究。E-mail：dingwanfei_@163.com。

P642.2；P315.9

A

1674-0696(2017)11-061-05

(责任编辑：朱汉容)