对流换热系数对厚板焊接残余应力应变研究

何雄君，何江源

(武汉理工大学 交通运输学院，湖北 武汉 430060)

对流换热系数对厚板焊接残余应力应变研究

何雄君，何江源

(武汉理工大学 交通运输学院，湖北 武汉 430060)

主要考察了对流换热系数对厚板对接焊残余应力应变的影响，从而对现有的重要焊接构件(如桥梁大型锚拉板)的冷却方式给出参考，利用ABAQUS软件对焊接构件进行有限元模拟计算，通过改变对流换热系数数值大小来模拟冷却速度对厚板焊接残余应力应变的影响。研究表明：焊接区在不同冷却速度下计算结果没有数量级的差异，并且发现对流换热系数与构件焊后残余应力应变的影响也并非为单调线性的关系，在某一适中的对流换热系数条件下，厚板焊接的残余应力应变可以达到最小。

桥梁工程；焊接；对流换热系数；残余应力应变；X坡口平板对焊；生死单元

0 引 言

焊接是制造整体钢构件的重要环节，在许多重要的钢结构中，焊接的质量直接影响了结构的安全性，所以，在制作拼接较重要的受力构件时，如大型斜拉桥的锚拉板，过大的焊接残余应力会使材料使用产生隐患，笔者针对该类隐患，研究了不同对流换热系数下对焊接残余应力应变的影响，评价了对流换热系数对厚板焊接时残余应力应变的影响程度。

对流换热是日常高温物体冷却的主要原因，介质、流动性、温差等都会对其产生比较大的影响，焊接板焊缝区与周围环境发生热交换过程的速率可直接由对流换热系数反映。目前国内外大量学者从热学的角度对该系数进行了比较充分的研究，对于对流换热系数在不同条件下的取值，拥有了比较全面的数据。然而关于这一数值的改变所引起的力学问题却鲜有研究，由于在不同环境中的对流换热系数的取值差距非常显著(物体在空气中的对流换热系数视情况取为3～100，在水中取为200～15 000)，这一系数对焊接后的残余应力应变影响情况还不太明确，因此笔者分别立足于厚板焊接的残余应力应变问题，单独研究了这一系数在不同数量级下的取值对焊接残余应力应变的影响，并初步评估了其影响程度，这对研究厚板焊接质量的提高具有参考作用。

1 有限元模型

笔者采用热-弹-塑性有限元方法来模拟Q235钢X型坡口对接焊温度场、应力和变形，着重讨论对流换热系数对焊接残余应力和变形的影响。在热弹塑性有限元分析中，采用热力耦合的方式进行计算，即同时进行温度场与应力场的计算，然后将计算结果加入到应力计算模型中进行应力、应变和变形的求解。模拟采用的焊件尺寸为 400 mm×800 mm×36 mm，有限元模型如图1。为了兼顾计算精度和计算效率，在网格划分时，近焊缝区划得细密，远焊缝区划得相对粗大。有限元模型的节点总数14 484，单元总数为23 250。笔者运用 ABAQUS/Standard 通用分析模块求解温度场和应力场。在温度场计算的过程中，采用8节点6面体单元DC3D6T来进行计算，在应力场计算的过程中，采用与温度场对应的8节点6面体单元C3D6I来进行计算。

图1 网格化分Fig. 1 Mesh of the model

1.1 热分析

在温度场计算时，常见的热源模型有高斯热源和双椭球热源模型，由于热源模型对焊件的残余应力影响不大[1]，本模型共计11道焊缝(图2)，根据实际焊接热源的移动特点和电弧的能量分布规律，选用J. GOLDAK等[2]提出的双椭球热源模型来模拟焊接热输入，并采用生死单元的处理方法。除了考虑工件中的热传导外，同时还考虑了熔池的结晶潜热。由于焊缝金属与母材的热物理性能差别很小，笔者假定整个有限元模型具有与母材相同的热物理性能参数[3]。在模型中，利用牛顿法则和波尔茨曼定律分别考虑了工件与外部环境的对流和辐射[4]。

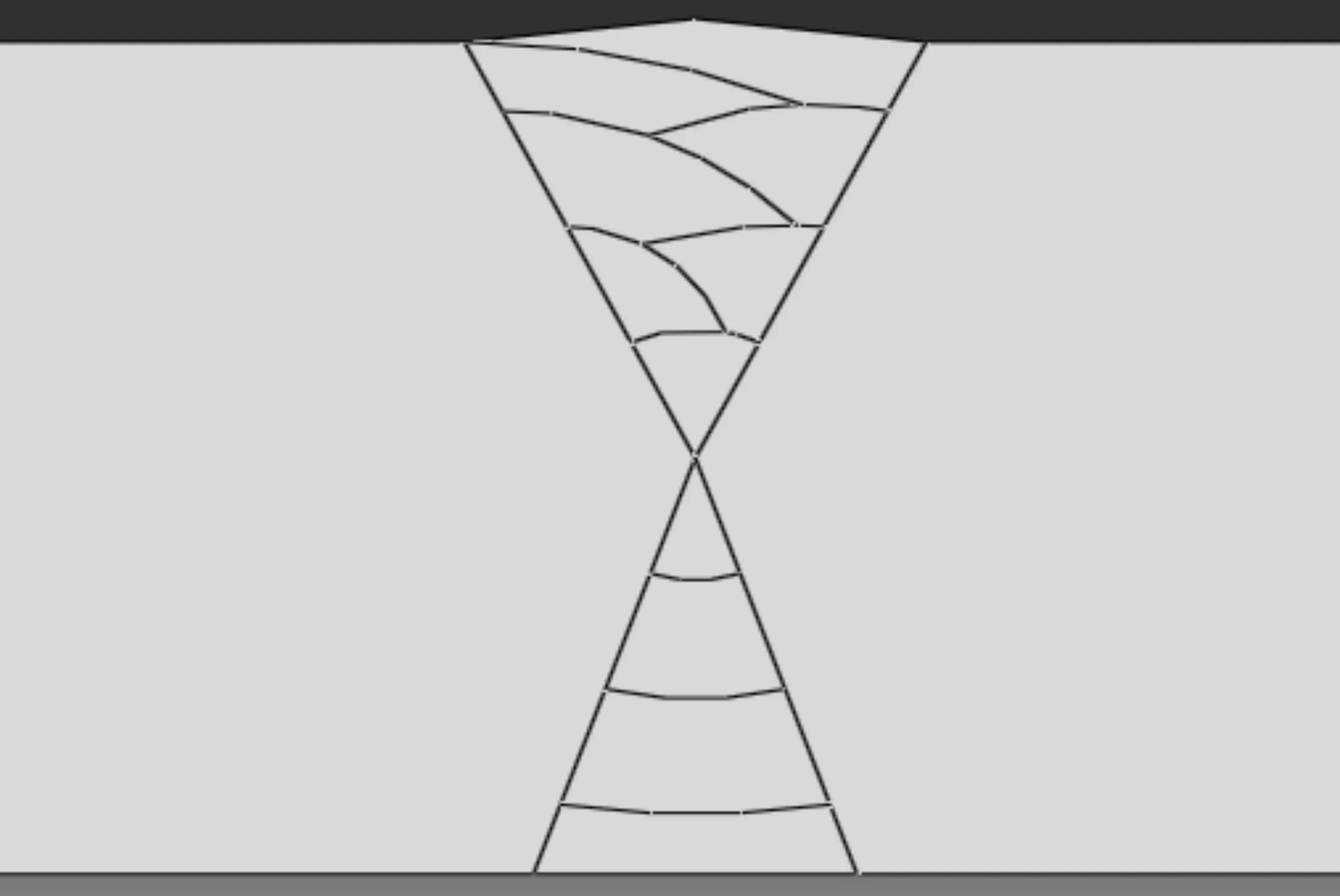
图 2 坡口形式及焊道布置Fig. 2 Groove form and arrangement of weld passes

在建模过程中，根据一般焊接情况，设置每一道焊缝的冷却时间为100 s，由于对流换热系数为20时冷却速度相对较慢，故为其设置了10 000 s的最终冷却时间，以便更接近终态，其它两个模型最终的冷却时间设置为3 000 s[5]。

在焊接温度场传热分析中，散热边界条件考虑对流散热和辐射散热两种热传导方式[6]。热循环过程中，在熔池周围辐射热损失占主导地位，而远离熔池的母材区域对流热损失占主导地位，笔者采用等效对流散热系数来表示这两种散热导致的热损失，其中等效对流换热系数h描述如下：

(1)

式中：T0为初始坏境温度，常温下T0=293 K；ε为辐射系数，取值为0.8；σ为史蒂芬-玻尔兹曼常数，取值为5.67×10-8J/(m2K4s)。文中对流换热占据主导地位。

焊接材料以Q235钢为例，其各项参数如表1。

表1 Q235钢材料特性Table 1 Characteristics of Q235 steel

1.2 应力与变形计算

在热力耦合计算中，忽略应力应变对热分析的影响，将温度场计算结果作为荷载施加到力学模型上，求解残余应力[7]。在应力计算中，采用Mises屈服准则，忽略相变应变和加工硬化对残余应力的影响。模型的焊接变形包括角变形、横向收缩及纵向收缩，本实验主要考察角变形引起的竖向位移分量U3[8]。

1.3 边界条件和初始条件

其力学边界条件如图3，考虑到真实的焊接情况，CD平面限制沿z方向的位移(翻转后为AB平面)，并同时给与钢板两个侧面以xy的双向约束。默认坐标系为：沿焊缝为x方向，垂直于焊接板面为z方向，沿钢板侧面为y方向。初始温度设置为20oC，辐射换热系数取0.8，对流换热系数取值分别为20、200、2 000 J/(m2·s·℃)3个级别。

图3 边界条件
Fig. 3 Boundary conditions

2 计算结果与分析

2.1 焊接中心区温度变化规律

图4为焊接中心区域温度变化规律，由图4可见，当对流换热系数取20，接近弱对流空气中的情况时，焊接板冷却至常温时间达到1 h以上，而在对流换热系数取2 000时，此时比较接近在强对流水中冷却的情形，冷却至常温只需数分钟。对流换热系数每增加一个量级，冷却至常温的时间将缩短60%以上。不同的冷却环境对焊接过程温度变化影响显著，在这一不同冷却环境下，我们需要进一步研究对流换热对其他因素的影响。

图4 不同对流换热系数下温度变化Fig. 4 Temperature changing with different convective heat transfer coefficients

2.2 对流换热系数对残余应力及变形的影响

图5为不同冷却条件下焊接板中剖面的变形云图，剖面法向为x方向。图中显示的是沿z方向的位移，由图5可见，在未考虑钢板自重的情况下，钢板的最大与最小位移均位于焊缝中，其变形均很小。当对流换热系数越大时，其相对位移的最大值越小。但对比这3组云图看来，小的对流换热系数会导致温度对位移影响的范围变大，其主要原因是过慢的冷却使得高温区的弹性模量处于较低值，更容易随时间推移产生微小变形。

图5 不同对流换热系数下的变形Fig. 5 Deformation with different convective heat transfer coefficients

图6为不同对流换热系数下，焊接板的残余应力分布，从图6可见，焊接板只受主拉应力，并主要集中在焊接区域,如图7。为了进一步了解残余应力在不同位置的分布情况，分别对焊接板沿y方向-0.4、-0.3、-0.2、-0.1、0、0.1、0.2、0.3、0.4 m处9个切面取某相同单元进行应力观察，数据如图8。

综合图6～图8可知：

1)在焊接的中心区域均存在较大的残余拉应力，且远离焊缝和热影响区的应力逐渐递减，所有单元均未出现残余压应力。对于对称坡口，先焊一面会对后焊一面产生约束，因而后焊面残余应力峰值要大于先焊面。

2)3种情形的最大应力值相差不大，事实上其相差范围均在100 MPa以内。前人经验表明，随着对流换热系数的减小，残余应力有所减小，但本次实验中，随着对流换热系数的改变，应力峰值并不是呈单调线性变化，这与经验中所猜想的情况有所出入。原因是过慢的冷却会导致高温区对钢板的影响时间变长，这也是造成残余应力增大的因素之一。

3) 3种对流换热系数下，残余应力峰值均在230 MPa左右，超过了Q235的屈服应力，说明Q235钢材不适合此种类型的平板对接，需要重新设计焊接方案或者采用更高强度的钢材。

图6 不同对流换热系数下的主应力Fig. 6 Principal stress with different convective heat transfer coefficients

图7 不同对流换热系数下的主应力Fig. 7 Principal stress at different convective heat transfer coefficient

图8 不同对流换热系数下的切片内力影响Fig. 8 Influence of section internal force with different convective heat transfer coefficients

3 结 语

在36 mm厚壁钢板进行X坡口对接焊时，焊后在靠近焊缝区域会出现较大的残余拉应力，残余拉应力随着远离焊缝迅速减小，未出现残余压应力。在不同对流换热系数下，焊接板的残余应力不会出现单调性的变化，过慢的冷却会使局部高温区的影响时间增加，过快的冷却会使局部温差增大，这些因素都会导致残余应力的增加。另外残余变形程度直接受对流换热系数的影响，快速的冷却可以降低变形值。所以应该采取合适的焊接工艺或者控温措施，使焊接板的冷却速度在一个合适的范围内。

[1] American Welding Society．WeldingHandbook,Vol.1[M]． 8th ed. Miami: American Welding Society, 1991．

[2] GOLDAK J, CHAKRAVARTI A, BIBBY M. A new finite element model for welding heat sources[J].MetallurgicalandMaterialsTransactionsB, 1984, 15(2): 299-305.

[3] 钟群鹏，赵子华.断口学[M]. 北京：高等教育出版社, 2006.

ZHONG Qunpeng, ZHAO Zihua.Fractography[M].Beijing: Higher Education Press, 2006.

[4] 杨燕. 焊接热源对钢结构焊接应力的影响[J]. 铸造技术, 2014(2): 374-377.

YANG Yan. Influence of welding heat source on welding stress of steel structure[J].FoundryTechnology, 2014 (2): 374-377.

[5] 谭伯聪,谢德,李荣锋,等.超厚钢板焊接残余应力剖析[J].钢铁研究,1993(5):35-39.

TAN Bocong, XIE De, LI Rongfeng, et al. Analysis on residual welding stress of extra thick steel plate[J].ResearchofIron&Steel, 1993(5): 35-39.

[6] 鲁鹏, 赵耀, 袁华. 边界条件对船用厚板高强钢焊接残余应力的影响研究[J]. 中国造船, 2013(2):124-132.

LU Peng, ZHAO Yao, YUAN Hua. Study on the influence of boundary conditions on welding residual stresses of marine heavy plate steel[J].ShipbuildinginChina, 2013 (2): 124-132.

[7] 邓宁华. 风速风向对墙体表面换热系数影响的实验研究[D].长沙： 湖南大学, 2001.

DENG Ninghua.ExperimentalStudyonInfluenceofWindSpeedandWindDirectiononHeatTransferCoefficientofWallSurface[D].Changsha: Hunan University, 2001.

[8] 李彬. 建筑表面对流换热系数的规律特征研究[D]. 西安: 西安建筑科技大学, 2014.

LI Bin.StudyontheLawofConvectiveHeatTransferCoefficientofBuildingSurface[D].Xi’an: Xi’an University of Architecture and Technology, 2014.

ResidualStressandStrainofConvectiveHeatTransferCoefficientonThickPlateWelding

HE Xiongjun, HE Jiangyuan

(School of Transportation, Wuhan University of Technology, Wuhan 430060, Hubei, P.R.China)

The impact of convective heat transfer coefficient on the residual stress and strain of butt welding was mainly investigated. Therefore, the reference for the cooling method of the existing important welding components (such as the bridge large tensile anchor plate) was given. The finite element simulation calculation of the welding parts was carried out by ABAQUS software, and the numerical value of convective heat transfer coefficient was changed to simulate the impact of cooling speed on residual stress and strain of thick plate welding. The research shows that: the calculation results of the welding zone with different cooling speed have no difference in magnitude, and it is also found that the influence of the convective heat transfer coefficient on the residual stress and strain of the component after welding is not monotonous linear relationship. In a moderate condition of convective heat transfer coefficient, the residual stress and strain of thick plate welding can reach the minimum.

bridge engineering; welding; convective heat transfer coefficient; residual stress and strain; X groove butt joint; birth-death element

10.3969/j.issn.1674-0696.2017.11.02

2016-04-06；

2016-12-10

国家自然科学基金项目(51178361)

何雄君(1966—)，男，湖北蕲春人，教授，博士后，主要从事桥梁安全检测方面的研究。E-mail：1208085086@qq.com。

何江源(1991—)，男，湖北咸宁人，硕士，主要从事桥梁结构方面的研究。E-mail：325246264@qq.com。

U441+.5;TG40

A

1674-0696(2017)11-007-04

(责任编辑：谭绪凯)