土体材料极限应变影响因素的敏感性灰关联分析

王 乐，郑颖人,2，辛建平，李 晟

(1.后勤工程学院 军事土木工程, 重庆 401311; 2.重庆市地质灾害防治工程技术研究中心， 重庆 400041)

【基础理论与应用研究】

土体材料极限应变影响因素的敏感性灰关联分析

王 乐1，郑颖人1,2，辛建平1，李 晟1

(1.后勤工程学院 军事土木工程, 重庆 401311; 2.重庆市地质灾害防治工程技术研究中心， 重庆 400041)

阿比尔的等提出了极限应变判据及其稳定分析方法，采用数值极限分析方法求出岩土材料在单向受力下的极限应变，以极限应变作为岩土材料的破坏标准，结合强度折减法计算岩土工程破坏的起裂、演化过程和稳定安全系数。文章介绍了极限应变的概念和计算方法，采用数值极限分析方法中的有限元荷载增量法求得了不同参数土体材料的极限应变。采用灰关联法，分析与土体相关8个影响因子对极限应变的敏感性，由大到小分别为：弹性模量、黏聚力、网格数、内摩擦角、泊松比、模型尺寸、土体重度、抗拉强度。

极限应变；敏感性；灰关联分析方法；影响因素

岩土工程广泛应用极限分析方法，传统极限分析方法[1-2]基于屈服条件和整体破坏条件可以导出岩土工程的稳定安全系数，但存在如下两个缺点，一是要事先知道材料的整体破坏面，二是无法知道破坏全过程，包括哪一点先开始破坏，破坏的发展过程，以及开裂的安全系数等。近年来，随着数值分析方法的发展，建立了数值极限分析方法[3-6]，即用数值方法进行极限分析，求出相应的安全系数。这种方法也是基于整体破坏条件，其优点是不需要事先知道破坏面，有很广的适用性，但同样存在第二个缺点。而且弹塑性力学中都是研究任意点的应力、应变、位移，屈服与破坏，更需要点破坏条件。

最近，阿比尔的、郑颖人等提出了极限应变点破坏准则[7]，开创了基于点破坏的极限分析方法。采用此方法可得到材料从点破坏逐步到整体破坏的全过程。这种方法刚刚起步，逐渐被学术界认可[7-12]，当然还需要继续发展和深化认识。

极限应变通常是指材料相对于相应峰值应力的应变值，在混凝土工程[13]中早有应用，但无法计算求得，一般通过测试获得极限应变。阿比尔的、郑颖人等提出了求取极限应变的数值计算方法，使极限应变易求取。本研究对影响极限应变的因素进行敏感性分析，主要分析了黏聚力、内摩擦角、弹性模量、泊松比、网格数、模型尺寸、土体重度、抗拉强度对极限应变的影响规律，并通过灰关联法找出影响极限应变主要因素的排序。

1 灰关联分析的基本原理和方法

灰关联分析属于灰色系统理论，它的特点是即使数据资料有限，也可以用关联度表示自变量和因变量的相关联程度，关联度越大，两者的关联程度越强。具体的原理和计算方法见《土工格栅加筋土挡墙稳定性影响因素敏感性分析》[14]。

2 极限应变的概念和计算方法

2.1 极限应变的概念

岩土类材料在压力与剪力的作用下通常发生压剪破坏。随着荷载的不断增大，岩土类材料由弹性阶段进入塑性阶段，最后达到破坏。在强度理论中屈服是指材料初始屈服，它是弹塑性的分界点。进入塑性后材料的性质变化，但可以继续承载，而破坏表示材料承载力降低和丧失，破坏也是一个渐进过程。峰值以后材料进入软化阶段，出现局部宏观裂隙，直至整体破坏裂隙贯通整体，强度完全丧失或者留下残余摩擦强度。

极限分析常采用理想弹塑性模型，图1中理想弹塑性应力—应变曲线表现为应力不变，应变增大，可见若用应力来表述，无法反映材料在塑性阶段的变化过程，它只是破坏的必要条件而非充要条件，不能作为破坏准则。但若采用应变表述，则材料初始屈服时具有弹性极限应变γy，当材料屈服后塑性应变逐渐增大，达到破坏时具有弹塑性极限应变γf。因此材料的极限应变是破坏的充要条件，可作为点破坏准则。

当采用数值方法时，可用大小合适的单元来模拟点。材料中某单元达到塑性极限应变而破坏时，可作为材料点破坏的判据；当材料破坏点发展直至贯通时，认为材料已发生整体破坏，可作为材料的整体破坏判据。

图1 理想弹塑性应力-应变曲线

2.2 极限应变的计算

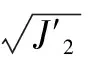
图2 计算模型

弹性模量E/MPa泊松比υ重度ρ/(kN·m-3)黏聚力C/kPa摩擦角φ/(°)抗拉强度σb/kPa10．00．3020．01020．00

图4为12个关键点的剪应变随荷载增加的曲线，由图可知临近破坏时剪应变最大的点为8号点，所以单独取8号点的剪应变-荷载图进行分析求取极限应变。

图3 剪应变增量云图

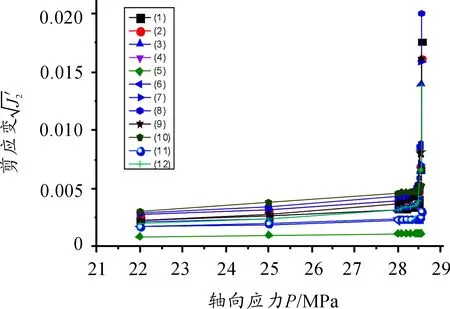
图4 轴向应力-剪应变关系曲线

如图5所示，应变刚开始增加缓慢，达到某一拐点后应变值产生突变，可认为拐点为破坏临界点，该点的应变值为极限剪应变值。由图5和表2可得拐点轴向荷载为28.50 kPa，对应的剪应变为5.88‰，故土体材料的极限剪应变为5.88‰。后续分析中所求极限应变均按照此方法计算。

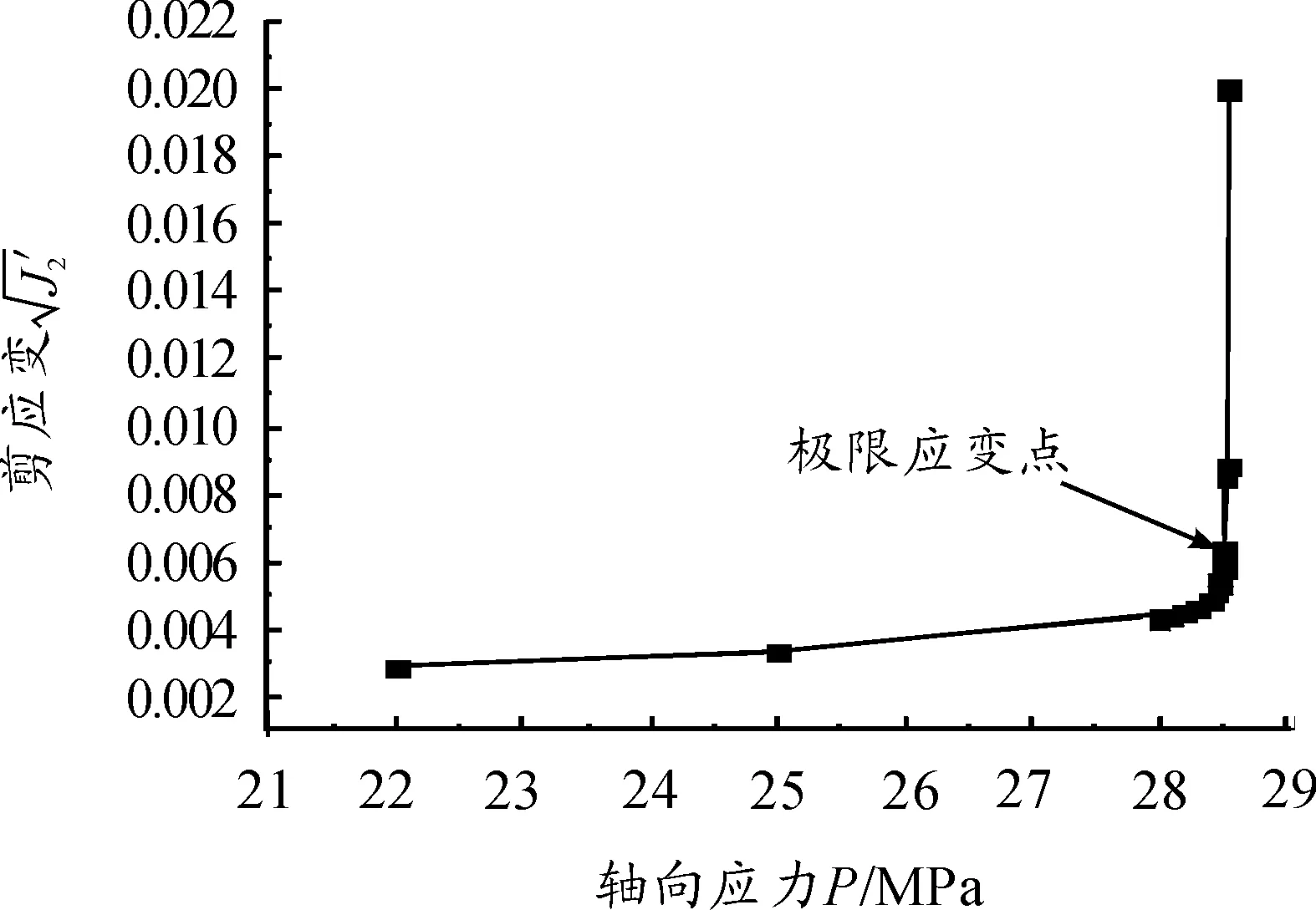
图5 8号点轴向应力-剪应变曲线

3 极限应变影响因素分析

3.1 计算模型

计算模型与2.2节所述模型一致，以表1所示的物理力学参数为基准，在此基础上通过修改某一个参数观察该参数变化对极限应变的影响。

3.2 影响因素分析

采用有限元荷载增量法[15-16]对初始模型进行稳定性分析，得到初始参数条件下的临界荷载为28.50 kPa，极限剪应变为5.88‰。下面分别研究黏聚力、内摩擦角、弹性模量、泊松比、网格数、模型尺寸、土体重度、抗拉强度对极限应变的影响规律。

表2 8号点轴向荷载—剪应变坐标值

3.2.1 黏聚力对极限应变的影响

表3给出了不同粘聚力下的土体极限剪应变。图6为粘聚力与极限荷载与极限应变的关系曲线。对其进行拟合，由拟合式知极限应变随粘聚力的增加而增大，呈线性关系。

表3 不同黏聚力对应的极限应变值

3.2.2 内摩擦角对极限应变的影响

表4中给出了不同内摩擦角条件下的土体极限剪应变。图7为内摩擦角与极限荷载与极限应变的关系曲线。并对其进行拟合，由拟合式知极限剪应变随着内摩擦角的增加而增大，也呈线性关系。

图6 黏聚力与极限应变的关系

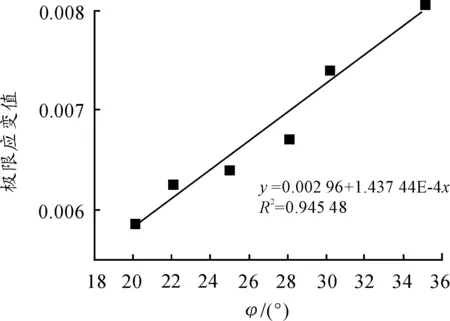
图7 内摩擦角和极限应变的关系

内摩擦角φ/(°)202225283035极限应变值/‰5．886．276．436．717．428．07

3.2.3 弹性模量对极限应变的影响

从表5可知曲线随着弹性模量的增大而下降。图8为弹性模量与极限剪应变的关系曲线，并对其进行拟合，由拟合式知两者呈二次函数关系。

表5 不同弹性模量对应的极限应变值

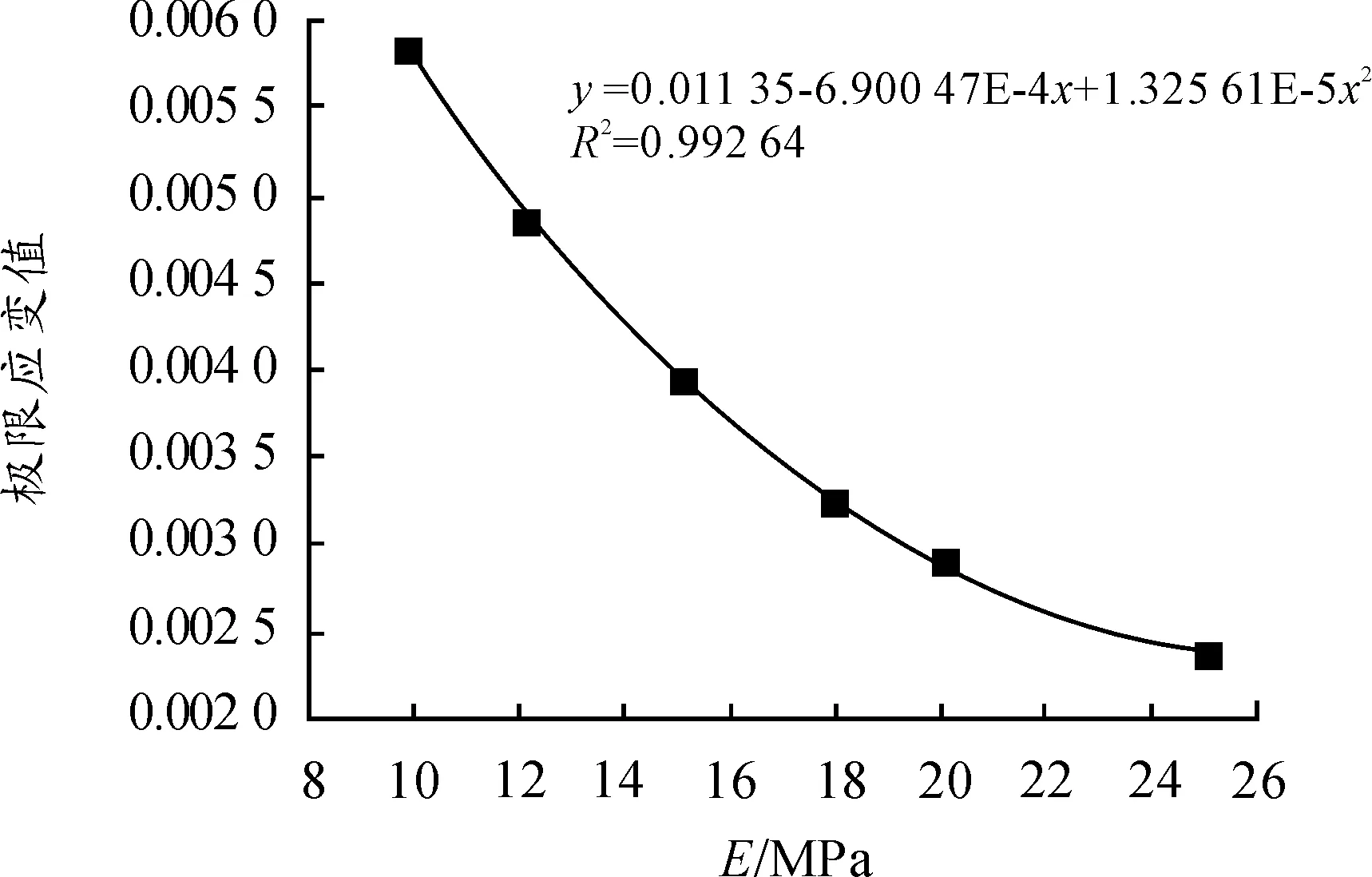
图8 弹性模量与极限应变的关系

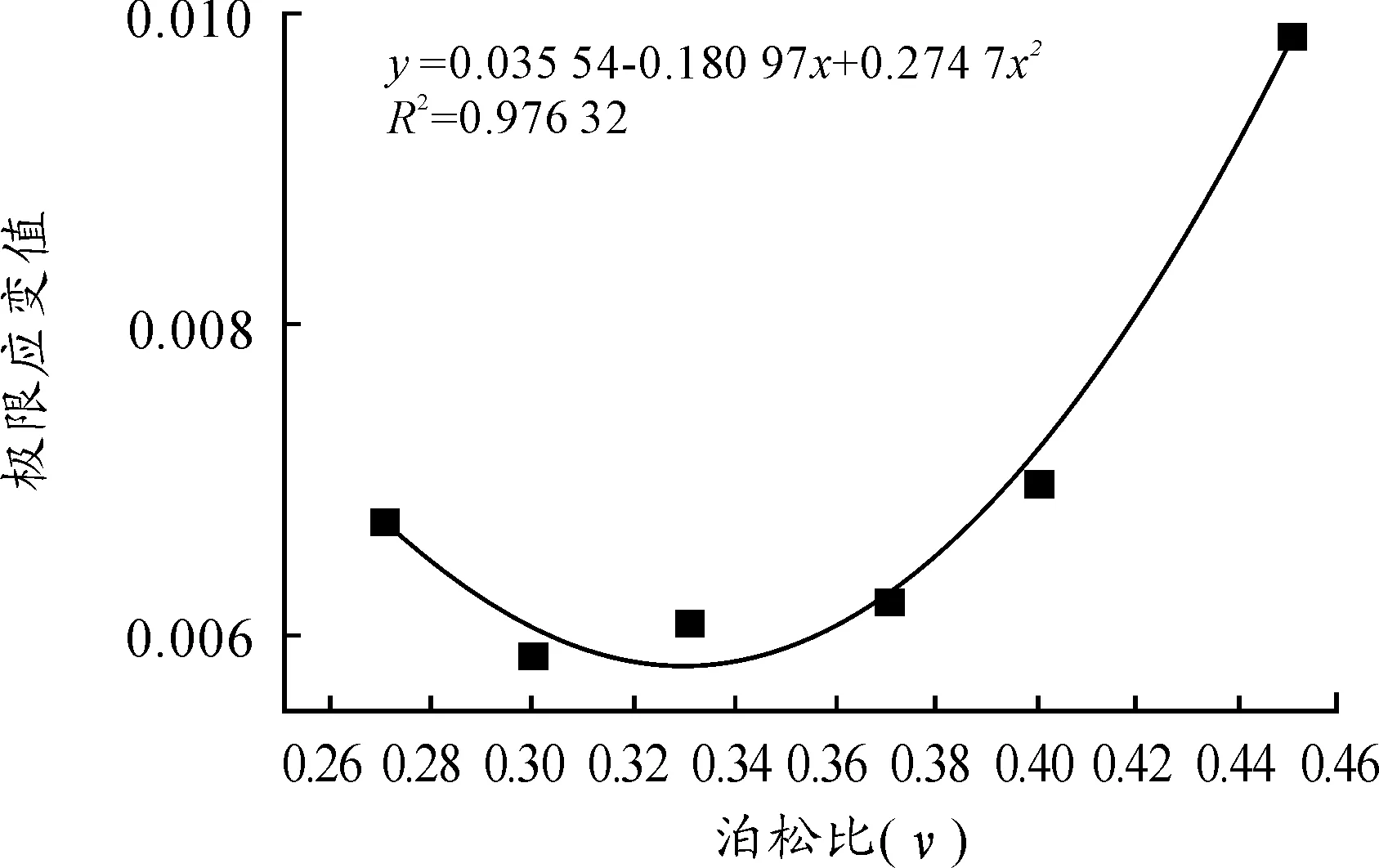
图9 泊松比与极限应变的关系

3.2.4 泊松比对极限应变的影响

由表6可以看出极限应变随着泊松比的变化呈先降再增的特点。图9为泊松比与极限剪应变的关系曲线，由拟合式知两者呈二次函数关系。

表6 不同泊松比对应的极限应变值

3.2.5 抗拉强度对极限应变的影响

由表7可知极限应变值并没有随着抗拉强度的改变而变化，说明抗拉强度对极限应变没有影响，图10对两者的关系曲线进行了拟合，为一条水平线。值得一提的是，当抗拉强度为0时，极限应变发生突变，其结果为5.88‰。

表7 不同抗拉强度对应的极限应变值

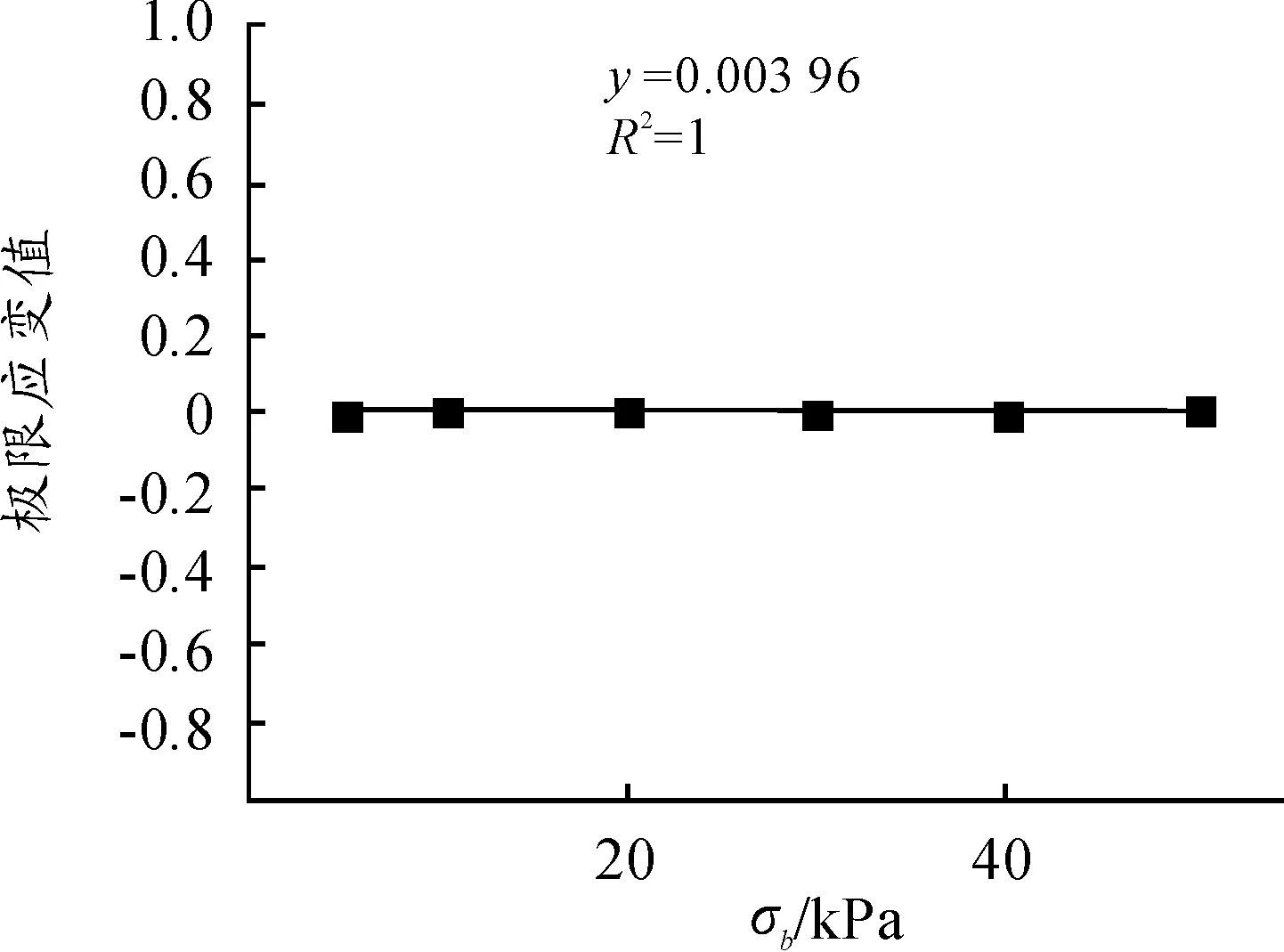
图10 抗拉强度和极限应变的关系

图11 模型尺寸与极限应变的关系

3.2.6 模型尺寸对极限应变的影响

由表8可以看出极限应变随着模型边长的增大呈现先增大后减小的规律，图11为关系曲线，由拟合式知两者呈二次函数关系。

表8 不同模型尺寸对应的极限应变值

3.2.7 重度对极限应变的影响

由表9可以看出极限应变随着模型重度的增大而呈现先增大后减小的规律，图12为重度和极限应变的关系曲线，由拟合式知两者呈二次函数关系。

表9 不同重度对应的极限应变值

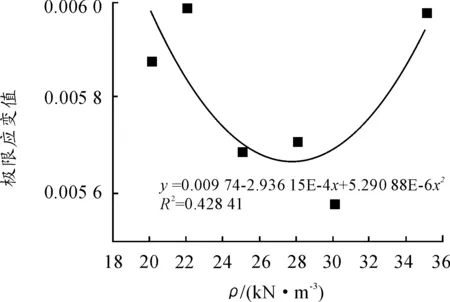
图12 重度和极限应变的关系

图13 网格数与极限应变的关系

3.2.8 网格数对极限应变的影响

由表10可以看出极限应变随着模型每边网格数的增加而不断增大，图13为网格数和极限应变的关系曲线，由其中的拟合式知两者呈一次线性函数关系。

表10 不同网格数对应的极限应变值

4 8种影响因素的敏感性灰关联分析

依据以上计算结果，建立比较矩阵X和参考矩阵Y。

区间相对值化后进而得到差异矩阵Δ,其中：Δmax=max(Δij)=1; Δmin=min(Δij)=0。分辨系数取为0.5，可得灰关联系数矩阵γ：

则关联度序列等于：

A=(0.961 6 0.912 1 0.991 0 0.689 1 0.602 8 0.692 5 0.622 8 0.922 7)

按敏感性大小排列，最后得到：弹性模量>黏聚力>网格数>内摩擦角>泊松比>模型尺寸>土体重度>抗拉强度。

5 结论

1) 采用数值极限分析方法中的荷载增量法求得不同岩土类材料的极限应变，提供了岩土工程点破坏条件和整体破坏条件。

2) 分析了黏聚力、内摩擦角、弹性模量、泊松比、网格数、模型尺寸、土体重度、抗拉强度对极限剪应变的影响，并给出了它们的关系曲线拟合式。

3) 采用灰关联分析方法对影响因素的敏感性进行分析，按敏感性大小得到排序为:弹性模量>黏聚力>网格数>内摩擦角>泊松比>模型尺寸>土体重度>抗拉强度。

[1] 张炜.极限平衡法研究现状[J].科技信息,2009(10):420.

[2] 王志福.谈极限平衡法的研究现状[J].山西建筑,2013(5):60-61.

[3] 郑颖人.岩土数值极限分析方法的发展与应用[J].岩石力学与工程学报,2012,31(7):1297-1316.

[4] 郑颖人,赵尚毅,李安红,等.有限元极限分析法及其在边坡中的应用[M].北京:人民交通出版社,2011.

[5] 刘祥沛,郑颖人,董天文.桩基础极限荷载有限元判定方法研究[J].后勤工程学院学报,2016(3):18-25.

[6] 杨森,李秀地,赵帅军,等.基于强度折减法的海底隧道强震破坏机理[J].后勤工程学院学报,2015(2):1-6.

[7] 阿比尔的,冯夏庭,郑颖人,等.岩土类材料应变分析与基于极限应变判据的极限分析[J].岩石力学与工程学报,2015,34(8):1552-1560.

[8] XIN J,ZHENG Y,WU Y,et al.Analysis of Tensile Strength’s Influence on Limit Height and Active Earth Pressure of Slope Based on Ultimate Strain Method[J].Advances in Materials Science and Engineering,2017(7):1-8.

[9] XIN Jianping,ZHENG Yingren,LI Xiudi,et al.Exploration on Safety Assessment Method Based on Strain for Immersed Tube Tunnel[J].Electronic Journal of Geotechnical Engineering,2016(20/21):6755-6770.

[10] XIN Jianping,Zheng Yingren,ABI ERDI,et al.Stability Analysis by Ultimate Strain Criterion in Slope Engineering[J].Electronic Journal of Geotechnical Engineering,2016(21/24):7879-7905.

[11] LI Sheng,XIN Jianping,ZHENG Yingren,et al.Influence Factors Analysis and Application of Ultimate Strain of Geomaterials[J].Electronic Journal of Geotechnical Engineering,2016(21/22):6907-6919.

[12] 阿比尔的,郑颖人,冯夏庭,等.极限应变法在圆形隧洞稳定分析中的应用[J].应用数学与力学，2015,36(12):1265-1273.

[13] 李爱群,王铁成.混凝土结构设计原理[M].6版.北京:中国建筑工业出版社,2015.

[14] 宋雅坤,郑颖人,刘一通,等.土工格栅加筋土挡墙稳定性影响因素敏感性分析[J].后勤工程学院学报,2010(3):1-7.

[15] 郑颖人,赵尚毅.有限元强度折减法在土坡与岩坡中的应用[J].岩石力学与工程学报,2004,23(19):3381-3388.

[16] 郑颖人,孔 亮.岩土塑性力学[M].北京:中国建筑工业出版社，2010.

SensitivityGrayRelationAnalysisofInfluencingFactorsofUltimateStrainofSoil

WANG Le1, ZHENG Yingren1,2, XIN Jianping1, LI Sheng1

(1. Military Civil Engineering,Logistics Engineering College, Chongqing 401311, China; 2.Engineering Technical Research Center for Prevention and Control of Geological Disasters in Chongqing, Chongqing 400041, China)

Abi Erdi and others put forward ultimate strain criterion and stability analysis method based on it.The numerical limit analysis method is applied to solve the ultimate strain of geomaterials; the ultimate strain under uniaxial pressure was got as a new failure criterion to judge the failure of materials and to solve geotechnical failure surface position, shape, evolution process and the stability safety factor through strength reduction method. In this paper, the concept and calculation method of ultimate strain are introduced. The finite element load increment method in numerical limit analysis method is used to obtain the ultimate strain of soil material of different parameters. It’s the sensitivity of the eight factors which influence ultimate strain that is analyzed by means of gray relational analysis method, according to the size in the order:elastic modulus, cohesion, grid number, internal friction angle, Poisson’s ratio, model size, unit weight of soil and tensile strength.

ultimate strain; sensitivity; gray relational analysis method; influence factor

2017-05-10；

2017-05-30

重庆市基础与前沿研究计划院士专项项目“岩土材料极限应变分析与破坏准则”(cstc2016jcyjys0002)

王乐(1993—)，男，硕士研究生，主要从事地下隧洞稳定性与数值分析研究。

郑颖人(1933—)，男，教授，中国工程院院士，博士生导师，主要从事岩土本构关系理论与数值分析及地下工程稳定性方面的教学与研究。

10.11809/scbgxb2017.10.036

本文引用格式：王乐，郑颖人，辛建平，等.土体材料极限应变影响因素的敏感性灰关联分析[J].兵器装备工程学报，2017(10):175-180.

formatWANG Le, ZHENG Yingren, XIN Jianping, et al.Sensitivity Gray Relation Analysis of Influencing Factors of Ultimate Strain of Soil[J].Journal of Ordnance Equipment Engineering,2017(10):175-180.

TU45

A

2096-2304(2017)10-0175-06

(责任编辑唐定国)