运输问题表上作业法补零规则的改进

林 磊

（广东技术师范学院 数学与系统科学学院，广东广州510665）

运输问题表上作业法补零规则的改进

林 磊

（广东技术师范学院 数学与系统科学学院，广东广州510665）

对运输问题表上作业法过程中，检验数计算出现负值，而方案却已经达到最优这种情况进行了分析，指出了其原因在于问题出现退化时进行补零操作的规则不明确，进一步给出了一种改进的补零规则以减少这种情况出现.

表上作业法；检验数；退化解；运筹学；运输问题

运输问题是运筹学的一个重要分支线性规划问题的特例［1］.对于一般线性规划问题，可以使用单纯形法来解决［2］.而运输问题由于其约束条件变量的系数矩阵的特殊性，可以使用比单纯形法更为简单的方式来处理，例如表上作业法［3］.图1给出了表上作业法的流程图.如图1所示，在得到某一个调运方案后，需要计算检验数来判断该方案是否达到最优.当检验数出现负值时，应该调整方案来获得更优的解.然而，有时，虽然检验数出现了负值，调运方案却已达到了最优.本文就这种情况形成的原因进行了分析，发现这是由于问题出现退化时进行补零操作的规则不明确而导致的.故而，本文设计了一种改进的补零规则减少此种情况的出现.

图1 表上作业法流程图

1 问题引入与分析

这一节将详细地描述本文所要解决的问题.为了便于理解，下面将结合具体的实例来引出问题.

例子1：已知运输问题的产销地的供需量与单位运价表如表1所示，用表上作业法求解其最优解.

解：这是一个产销平衡的运输问题，文中单位运价用符号cij表示，从i地销往j地的运量用符号xij表示，检验数用符号σij表示.第一步通过Vogel法［4-5］寻找初始调运方案.在第一轮计算行列最大差时，出现第一行和第一列的最低和次低运费的差值都为8，是最大的运费差，所以按照Vogel法的规则，可选择划掉第一列，设置x31=5.由于x31所在行的产量等于其所在列的销量，还要同时划掉第三行，并可以设置第三行或是第一列除去x31的某一格运量为0，并将此格所代表的变量视为基变量.假设设置x11=0，继续使用Vogel法，得到初始调运方案如表2所示.

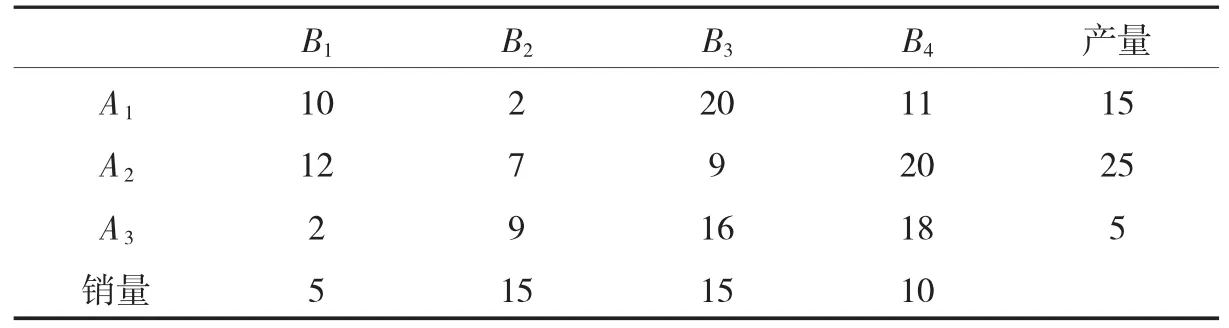
表1 产销供需量与单位运价表

表2 初始调运方案

表2中括号里面的数字代表对应的行产地运往列销地的运量.接下来计算空格变量的检验数.使用闭回路法［1］算出检验数为：

σ13=16，σ21=-3，σ24=4，σ32=14，σ33=20，σ34=15.

可以看出，检验数当中有负值，根据表上作业法该方案没有达到最优，需要调整.从σ21所对应的空格(A2,B1)出发，做一条除该空格外其余顶点都为有数字格的闭回路，如表3所示.由于这条闭回路上最大的调整值为0，所以调整之后的总运费是不会改变的.换句话说，调整后的方案和原方案所对应的目标函数值是一样的.对这个闭回路，调整后，只有x11和x21有变化，x11从基变量0变成了非基变量0，而x21从非基变量0变成了基变量0.对新的方案，计算检验数，原来为正的检验数依然为正的，新的非基变量x11的检验数此时也为正，且刚好是原非基变量x21检验数的相反数.因此，由于所有非基变量的检验数都为正，新方案已达到最优.

表3 (A2,B1)闭回路

显然，初始方案与新的方案的目标函数值是相等的.由于新的方案达到了最优，所以初始方案也达到了最优.然而初始方案的检验数却有负数值.为什么会出现这种现象？原因在于，求初始方案的时候出现要同时划去一行和一列的情况（称为退化），在这个时候为了使基变量的个数不减少，需要在划去的行列中随机选择一格赋值0作为基变量.选择哪一格补0按传统的规则是随机挑选的，这种规则会导致表上作业法出现以上的漏洞.因为，选任何一格补0最后得到的调运方案所计算的总运费是一样的.假设，在所有这些方案中，有一种方案已知是最优的且对应的检验数皆为正值.那么，其它方案中一旦有检验数为负值的情况就都属于所介绍的这种现象.为了减少这种情况出现，下一节给出了改进的补零规则.

2 改进的补零规则

根据上一节的例子，可以看出，如果一个方案已经达到最优，此时出现了退化.传统的补零规则是随机选取同时划去的行列中除最小运费之外的任意格做为基变量.假设补零的时候选取某一格为基变量，利用闭回路算法计算检验数时这一格的检验数恰好却出现了负值.那么就会出现检验数为负值，方案却已达到最优这种情况.为了减少这种情况出现的次数，本文给出了一种改进的补零规则：对运输问题进行表上作业法碰到退化解时，选择同时划去的行列中未添供销量格中运费最小的格补上0.

规则解释：不失一般性，假设需要同时划去的行列中未添供销量格子中最小运费格为(Ar,Bs).计算被划去行列中这些非基变量的检验数时，某些非基变量格的闭回路会以(Ar,Bs)格做为其回路顶点.对这些非基变量格计算检验数时，可以分为两种情况分析.一种是计算检验数时需要加上(Ar,Bs)格的运费crs，这种情况下(Ar,Bs)格贡献的是正数，不会导致检验数为负；另一种是计算检验数时需要减去(Ar,Bs)格的运费crs，这种情况下(Ar,Bs)格贡献的是负数，但由于所要计算检验数的非基变量格的运费按改进的规则是大于等于crs，两者相减得数非负，故也不会导致检验数为负.

3 结论

本文对运筹学中运输问题的表上作业法出现检验数为0方案却已最优的情况进行了分析，指出其原因是在同时划去行列时的补零操作过于随机.为了减少这种情况的发生，本文给出了一种改进的补零规则.

［1］胡运权.运筹学基础及应用[M].5版.北京：高等教育出版社,2015.

［2］唐四云.运输问题表上作业法中初始方案的改进[J].广东技术师范学院学报,2016,37（5）:39-42.

［3］张晓瑾,刘海生.运输问题的表上作业法中初始方案的优化[J].华北科技学院学报,2014,11（6）:73-75.

［4］何莉敏,李玉,于涛,等.Vogel法求解最大值问题[J].郑州大学学报（理学版）,2011,43（1）:25-28.

［5］贾春玉.运输问题新解法的探讨[J].系统工程学报,2004,19（2）:207-211.

Improvement in Zero Filling Rule of the Table-working Scheme in Transportation Problem

LIN Lei
（School of Mathematics and Systems Science,Guangdong Polytechnic Normal University,Guangzhou 510665,Guangdong,China）

While the table-working scheme is used to solve the transportation problem,there exists an exceptional situation,in which the solution is optimal but some check numbers of non-base variables are negative.The reason is that the rules of zero filling are not clear in the case of degeneration.In order to reduce the situation,an improved zero filling rule is presented.

table-workingscheme；checknumber；degenerationsolution；operationalresearch；transportationproblem

O152.7

A

1007-5348（2017）03-0019-03

2017-02-02

国家自然科学基金青年项（61601131）；广东省自然科学基金（2016A030313727）；广东省教育厅青年创新人才项目（2015KQNCX086）.

林磊（1982-），女，安徽潜山人，广东技术师范学院数学与系统科学学院讲师，博士；研究方向：快变信道.

（责任编辑：邵晓军）