长联大跨连续梁桥无缝线路布置方案

杨新文， 赵 亮， 宫 寅

(1. 陕西城际铁路有限公司， 西安 710065； 2. 中铁上海设计院集团有限公司， 上海 200070)

长联大跨连续梁桥无缝线路布置方案

杨新文1， 赵 亮1， 宫 寅2

(1. 陕西城际铁路有限公司， 西安 710065； 2. 中铁上海设计院集团有限公司， 上海 200070)

西安机场线渭河特大桥采用长联大跨连续梁，主桥连续梁联长900 m，最大温度跨度715 m，具有温度跨度大且多跨连续梁相接的特点，需合理设计无缝线路。针对该工况提出5个无缝线路布置方案，采用有限单元法进行无缝线路附加力计算，从钢轨强度、桥墩受力两方面进行方案比选后，现场调研国铁类似工况，确定最终推荐方案。得出结论：(50+8×100+50)m连续梁两侧梁端布置单向钢轨伸缩调节器，满足钢轨强度检算的要求且能有效减小相邻连续梁固定墩受力，无需布置双向钢轨伸缩调节器。

地铁； 长联大跨连续梁； 无缝线路； 钢轨伸缩调节器

1 工程概述

西安机场线渭河特大桥具有温度跨度大、多跨连续梁相接的特点，该工况无缝线路布置方案是设计难点[1-2]，其大桥主桥连续梁效果图见图1。桥跨布置为：(2×30+3×30+3×30+105+2×38.5+4×50+(50+8×100+50)+(60+111+94+100+60)+3×30+3×25)m。其中，4×50 m与(50+8×100+50)m连续梁的温度跨度为550 m；(50+8×100+50)m与(60+111+94+100+60)m连续梁的温度跨度为715 m。主桥(50+8×100+50)m连续梁位于直线、平坡地段，除系杆拱外均采用箱梁，箱梁截面刚度较大且本工况多为连续梁，因此不计算挠曲力[3]。轨道工程采用U75V定尺轨、DTⅦ2型扣件及支承块承轨台式道床。

图1 渭河特大桥主桥(50+8×100+50)m连续梁效果图Fig.1 Effect diagram of(50+8×100+50)m continuous girder of Weihe River grand bridge

2 设计参数

2.1列车荷载

地铁B2型车辆，轴重140kN，6辆编组，车长117m。设计最高行车速度100km/h。

2.2轨温与梁温差

根据《铁路无缝线路设计规范》(TB10015-2012)[4]，采用最高轨温Tmax=61.8℃，最低轨温Tmin=-20.6℃。参考郑西客专西安—咸阳段、大西客专西安—咸阳段、西安地铁3号线高架的锁定轨温，同时参考铁科院对郑西客专渭河桥地区长达1年的轨温监测数据[5]，设计锁定轨温采用25±3℃，则钢轨最大升温幅度ΔTumax=39.8℃，最大降温幅度ΔTdmax=48.6℃。桥梁均为混凝土梁，无砟轨道梁年温差ΔTb=30℃。

2.3线路阻力

采用DTⅦ2型扣件，支承刚度D=30 kN/mm，单个弹条扣件压力为4 kN，扣件间距为595 mm。采用常阻力垫板时，扣件阻力1Q-r1=8.07 kN/m/轨；采用小阻力垫板时，扣件阻力2Q-r1=5.04 kN/m/轨[6]。

3 强度检算

3.1轨底动弯应力

采用《铁路无缝线路设计规范》(TB10015-2012)附录A无缝线路钢轨强度检算，公式中各符号意义见该规范，其中速度系数α=0.6，轨道横向水平力系数f=1.25，偏载系数β=0[4]。

动弯矩Md=M0(1+α+β)=21.06kN·m；

3.2钢轨最大温度拉应力

钢轨最大温度拉应力为

σt拉=EαΔTdmax=2.478×48.6=120.43MPa。

3.3钢轨最大附加拉应力

采用铁科院VRF软件，利用有限单元法计算桥上无缝线路纵向力[7]。

计算原理为:梁轨相互作用力通过梁体传递于设有固定支座的墩台上，墩台产生挠曲变形，并通过固定支座带动梁体在纵向上位移，梁体上翼缘与钢轨之间的相对位移改变，从而引起梁轨相互作用力的重分布。由此可建立梁轨相互作用的计算模型，如图2所示。在计算模型中，k表示梁轨间纵向阻力系数，K表示桥梁下部结构的纵向刚度，EJ表示钢轨伸缩调节器或钢轨折断处，P为列车垂直荷载，Q为轨面制动力，ΔtR为钢轨温差，ΔtB为梁伸缩温差，长钢轨在桥梁两端的长度为任意长。计算模型表示第i座桥梁为连续梁，L1为固定支座左边温度跨度，L2为固定支座右边温度跨度。当L1或L2为零时，连续梁就成为简支梁的情况。因此，计算模型包括了连续梁桥和简支梁桥的无缝线路。

图2 梁轨相互作用有限单元法计算模型Fig.2 Finite element calculation model of bridge/rail interaction

建立有限单元模型，右侧(3～30)m简支梁+(3～25)m简支梁简化为(5～30)m简支梁[8]。比选5个无缝线路布置方案[9-10]，见表1。

表1 无缝线路布置方案

3.3.1有限单元计算模型

各方案的有限单元计算模型见图3。

3.3.2计算结果

1) 钢轨受力和梁轨位移。各方案的计算结果见图4，图中共3部分内容，上部为钢轨受力，中部为梁轨位移，下部为对应模型。钢轨最大附加力和最大附加应力见表2。

图3 各方案的有限单元计算模型Fig.3 The finiteelement computing model of different schemes

图4 各方案的计算结果Fig.4 The results of the calculation of different schemes

项目钢轨最大附加力/(kN/轨)钢轨最大附加应力/MPa方案1 常阻力扣件1241.2160.3方案2 小阻力扣件898.6116方案3 主桥两端设单向调节器487.963方案4 主桥两端设双向调节器487.963方案5 主桥跨中设双向调节器898.6116

由计算结果可知，不设调节器时，钢轨附加应力明显较大的位置为(50+8×100+50)m连续梁两侧梁缝处，其中(50+8×100+50)m连续梁与(60+111+94+100+60)m连续梁的梁缝处钢轨附加应力最大，采用常阻力垫板时为1241.2kN/轨，采用小阻力垫板时为898.6kN/轨。在(50+8×100+50)m连续梁两侧梁端设钢轨伸缩调节器时，钢轨最大应力位置为(60+111+94+100+60)m连续梁与相邻简支梁的梁缝处，为487.9kN/轨，采用单向钢轨伸缩调节器与采用双向钢轨伸缩调节器时的计算结果基本相同。(50+8×100+50)m连续梁跨中采用双向调节器时，无法减小连续梁梁端的钢轨应力。

2) 桥墩承受伸缩力T1见表3，5个方案T1对比见图5。

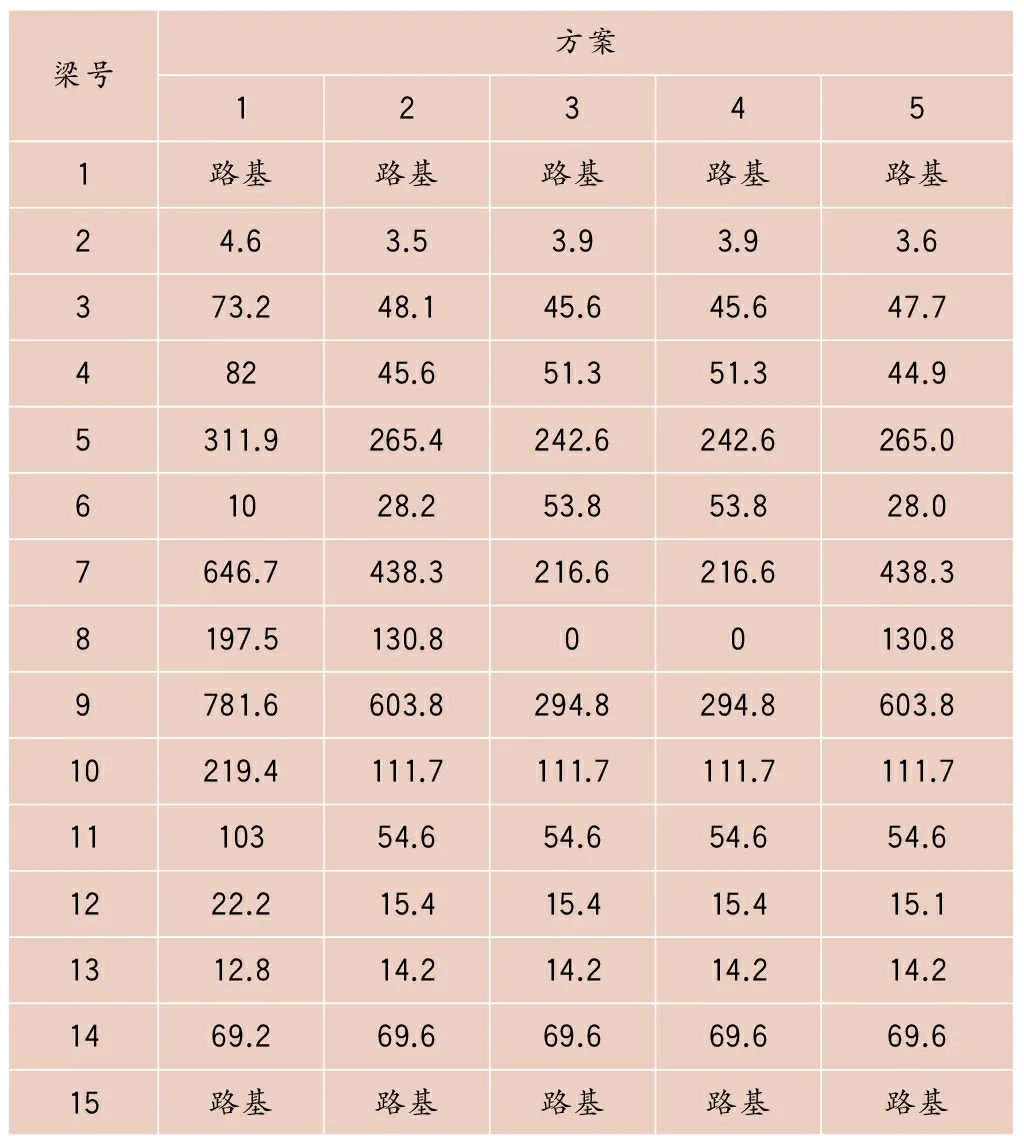
表3 桥墩承受伸缩力T1

图5 T1对比Fig.5 Comparison of T1

由表3和图5可知，(4×50)m连续梁和(60+111+94+100+60)m连续梁的固定墩受力较大。采用常阻力垫板时,(60+111+94+100+60)m连续梁的固定墩T1为781.6kN/轨；采用小阻力垫板时该力为603.8kN/轨；梁端设调节器后降低至294.8kN/轨，降幅达62.28%，梁端设单向钢轨伸缩调节器与设双向钢轨伸缩调节器对T1的影响相同。主桥跨中设调节器无法减小相邻连续梁固定墩受力。

3) 强度检算，结果见表4。

表4 钢轨强度检算

由表4可知，方案1全部采用常阻力垫板时钢轨强度检算不通过；方案2和方案5满足钢轨强度检算通过，但余量仅为21MPa，且(60+111+94+100+60)m连续梁的固定墩受力较大，为603.8kN/轨，对桥梁影响较大，因此不采用方案2和方案5。方案3和方案4的理论计算结果基本相同。因此，开展现场调研，进一步确定方案。

4 现场调研

调研郑西客专的连续梁+连续梁典型工况，调研点A，郑西客专二跨渭河特大桥采用了多组双向钢轨伸缩调节器[11]，调研点B采用了多组单向钢轨伸缩调节器，其中调研点B的桥跨布置见图6。

图6 调研点B的桥跨布置示意Fig.6 Bridge span arrangement of survey spot B

分析调研点B单向钢轨伸缩调节器的现场情况：图7中的1点为钢跨过梁缝与尖轨位于同一跨连续梁的基本轨与扣件的相对位移，现场测量相对位移约70～80 mm，从此处开始到基本轨跟端范围的基本轨与扣件相对位移为70～80 mm，尖轨与扣件无相对位移。图7中2点为梁缝处抬枕，基本轨与该处扣件存在较小的相对位移，该位移比1点小很多。图7中3点基本轨位于另外一侧连续梁，现场基本轨与扣件几乎无相对位移。现场观察调研点A双向钢轨伸缩调节器仅一侧发挥了作用，与调研点B的情况类似。因此，本工程设单向钢轨伸缩调节器即可，无需设置双向钢轨伸缩调节器。

图7 调研点B单向钢轨伸缩调节器的现场情况Fig.7 The scene of one-way REJ of survey spot B

5 结论

1) 推荐方案3，本工况在(50+8×100+50)m连续梁两侧设单向钢轨伸缩调节器后，可满足轨道强度检算要求，(60+111+94+100+60)m连续梁的固定墩受力仅为294.8 kN/轨，(4×50)m连续梁的固定墩受力仅为216.6 kN/轨，对桥梁影响小。

2) 理论计算及现场调研均表明，梁端设单向钢轨伸缩调节器可满足功能需求，无需采用双向钢轨伸缩调节器。

地铁工程采用连续长联大跨连续梁的工况较少，本文可为同类型工程无缝线路布置方案设计提供参考。

[1] 龚小平.长大跨度桥上无缝线路设计注意问题探讨[J].铁道建筑技术，2014(1)：31-34.

GONG Xiaoping. Study on design problems of CWR track on long span bridge[J]. Railway construction technology, 2014(1): 31-34.

[2] 孙井林，丁静波，李敏.上海地铁11号线(北段)无缝线路设计[J].铁道标准设计，2010(5)：14-17.

SUN Jinglin, DING Jingbao, LI Min. CWR design of Shanghai Metro Line 11[J]. Railway standard design, 2010(5): 14-17.

[3] 刘浩，魏贤奎，熊震威,等.线路纵向阻力形式对桥上无缝线路计算影响[J].铁道标准设计，2013(10)：61-64.

LIU Hao, WEI Xiankui, XIONG Zhenwei, et al. Influence of track longitudinal resistance form on the calculation of continuous welded rail sited on bridge[J]. Railway standard design, 2013(10): 61-64.

[4] 铁路无缝线路设计规范:TB10015—2012[S].北京：中国铁道出版社，2013.

Code for design of railway continuous welded cail: TB10015—2012[S]. Beijing: China Railway Publishing House, 2013.

[5] 徐玉坡，梁晨，蒋金洲.高速铁路轨温、梁温和环境温度的研究[J].铁道建筑，2015(1)：127-131.

XU Yupo, LIANG Chen, JIANG Jinzhou. Study on rail temperature, beam temperature and ambient temperature of high speed railway[J]. Railway engineering, 2015(1)： 127-131.

[6] 张凌之.小阻力扣件纵向阻力特性试验研究[D].成都：西南交通大学，2014.

ZHANG Lingzhi. Research on longitudinal resistance character of fastener with slight resistance[D]. Chengdu: Southwest Jiaotong University, 2014.

[7] 广中岩，高慧安.铁路无缝线路[M].北京：中国铁道出版社，2001：306-316.

GUANG Zhongyan, GAO Huian. Railway continuous welded rail[M]. Beijing: China Railway Publishing House, 2001: 306-316.

[8] 蔡敦锦，颜乐，李悦,等.桥梁参数对桥上无缝线路伸缩力的影响分析[J].铁道标准设计，2014(7)：30-34.

CAI Dunjin, YAN Le, LI Yue, et al. Analysis on how bridge parameters affect the expansion and contraction force of continuous welded rail on bridge[J]. Railway standard design， 2014(7)： 30-34.

[9] 曲村.高速铁路长大桥梁无砟轨道无缝线路设计理论及方法研究[D].北京：北京交通大学，2013.

QU Cun.Study on the design theory and method of ballastless continuous welded rail on long-span bridge in high-speed railway[D]. Beijing: Beijing Jiaotong University, 2013.

[10] 蒋金洲.广州轨道交通6号线白沙河大桥无缝线路布置方案探讨[J].现代城市轨道交通，2008(1)：22-24.

JIANG Jinzhou. Preliminary arrangement schemes of continuous welded rail for Guangzhou Metro Line 6[J]. Modern urban transit, 2008(1)： 22-24.

[11] 张岷.郑西客专二跨渭河特大桥无缝线路分析与研究[J].铁道建筑技术，2013(2)：51-54.

ZHANG Min. Analysis and research on the continuously welded rails on the two cross Weihe River bridge of Zhengzhou-Xi’an passenger dedicated line[J]. Railway construction technology, 2013(2)： 51-54.

Arrangement Schemes of Continuous Welded Rail for Long Span and Long Unit Continuous Girder Bridge

YANG Xinwen1, ZHAO Liang1, GONG Yin2

metro; long span and long unit continuous girder; continuous welded rail; rail expansion joints

10.3969/j.issn.1672-6073.2017.05.011

2016-11-26

2017-01-26

杨新文，男，本科，高级工程师，从事轨道交通轨道工程技术管理工作，1193070229@qq.com

U231

A

1672-6073(2017)05-0060-05

(编辑：郝京红)