一维渗透力与浮力1)

丁洲祥

∗(北京交通大学土木建筑工程学院，北京100044)

†(陕西省公路桥梁与隧道重点试验室，西安710064)

一维渗透力与浮力1)

丁洲祥∗,†,2)

∗(北京交通大学土木建筑工程学院，北京100044)

†(陕西省公路桥梁与隧道重点试验室，西安710064)

为简化分析，针对一维渗流问题，研究提出了土力学中渗透力和浮力的两种推导方法，作为传统的宏观尺度孔隙水隔离体法的有益补充.弹性力学平衡微分方程、土力学Terzaghi有效应力方程和流体力学简化Bernoulli方程构成本文分析渗透力和浮力的3个基本方程.在基本方程基础上，容易推导出相应的骨架和孔隙水两种隔离体的平衡微分方程，从而在静力平衡范畴内揭示渗透力和浮力的内涵.单位体积饱和土体的渗透力，源于总水头压力的梯度，而浮力则源于位置水头压力在竖向的梯度，这两者统一于骨架或孔隙水的平衡微分方程.实际工程关注的有效应力计算问题，一般可以直接应用3个基本方程来确定；只有在简化条件下可按渗透力和浮力计算土体中有效应力分布规律.还讨论了若干研究热点问题，重点探讨了当前一种渗透力新定义j=nγwi在形式上的合理性以及在实际应用中可能存在的风险，并验证了一维渗透力的一种经典精细化表述结果中考虑渗流速度时间导数的严谨性.在土力学渗透力和浮力问题研究中应重视和正确应用Terzaghi有效应力方程.

渗透力，浮力，有效应力原理，孔隙水压力，平衡微分方程

引言

经典土力学[13]中渗透力和浮力的概念并不简单,尤其是前者.过去一年多来，文献[4-7]从机理和公式推导等角度对这些既有概念加以研究，但尚无终论，如蒋中明等[6]认为“渗透力概念定义的不统一性以及推导过程的多样性、复杂性，是导致人们对渗透力的理解和应用产生误解的根源”.渗透力和浮力概念再度成为研究热点，这并非人们有意将简单问题复杂化，而是因为大量的既有相关认识仍有不足乃至相互矛盾之处.这轮研究和反思的一个主要特点是，注重研究方法的一般性、系统性和推导过程的严谨性.自2013年来，笔者对渗透力和浮力概念格外加以关注，并做了一些探讨性研究工作；现在意识到，可能存在一种观点——有时在某种意义上，土力学应用中使用的渗透力和浮力概念既不宜绝对肯定地当成唯一正确的方法，也不宜无视其合理性及意义.

见仁见智的学术研究，一般强调言贵有据.传统孔隙水隔离体法[19]将孔隙水假想地从土水整体中隔离开来，然后考虑浮力和渗透力两者的反力，据此分析孔隙水隔离体平衡条件，其中渗透力和浮力貌似不可或缺，容易被绝对肯定化.此外，渗透力和浮力概念在传统土力学中沿用多年，在评价渗透破坏等方面也有相关应用，这进一步强化了上述看法.然而，历史上也不乏相反的学术观点，对渗透力和浮力的研究意义基本上持否定的态度.

目前少有文献辩证地分析渗透力和浮力的上述绝对肯定与否定的观点，这就需要我们谨慎地求证开展辩证分析的力学依据.这样做的意义是，从新视角探求渗透力和浮力含义与适用条件的同时，也发现了推导土力学渗透力的一种新方法，该方法有别于目前仍占主流的孔隙水隔离体法.为避免将问题复杂化，本文仅针对一维问题进行分析：首先，提出渗透力和浮力的3个基本方程；然后，导出骨架和孔隙水两种隔离体平衡微分方程；其次，面向应用讨论有效应力计算中的等价性问题；最后，就同行最新研究成果进行了对比探讨.所得结论有助于深化对渗透力和浮力概念的认识.

1 一维模型和3个基本方程

饱和土体一维渗流模型如图 1所示.其中，Z坐标轴向上为正，坐标原点位于同质土层的底面z=0；土层厚度为H；土层底面、顶面和坐标z的水头分别为 h(0)、h(H)和 h(z).在图示条件下，h(0)＞h(H)，故渗流方向竖直向上，但模型也适用于h(0)≤h(H)的情况.坐标增量(z,z+dz)微元段dz内土体受力情况:上下端面对应应力增量(σ,σ+dσ)，体力为fzdz.

图1 渗透力和浮力的一维饱和土模型Fig.1 One-dimensional saturated soil model for seepage force and buoyance

1.1 总应力平衡微分方程

在土水整体总应力平衡微分方程方面，土力学和弹性力学是相通的——如果将土体固相在空间占据的区域明确定义为土体连续介质构形[10].这样可沿用弹性力学中一维静力平衡微分方程[11]

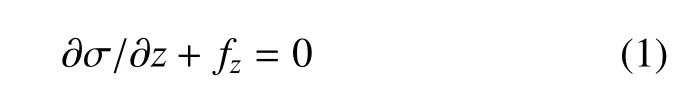
式中，σ是饱和土体总应力；fz是单位体积土体的体力，fz=−γsat；σ，fz均服从弹性力学符号约定.

1.2 Terzaghi有效应力方程

在固液两相应力分配关系上，土力学很有特色.经典土力学经常采用Terzaghi有效应力方程[3]

式中，σ′是土体有效应力；u孔隙水压力；σ,σ′和u按土力学习惯，常以受压为正.

1.3 孔隙水压力方程

在考虑渗流势能时，土力学借鉴了流体力学的部分经典成果.当忽略速度水头时，流体力学Bernoulli方程[12]更加简化，由此可得到

式中，h=h(z)是总水头；z是土中考察点的位置，z=0是零势参考面；γw是孔隙水单位体积的重度.

本文认为，上述3个基本方程是研究传统渗透力和浮力的联合控制方程.

2 骨架平衡微分方程与渗透力和浮力

2.1 骨架平衡微分方程与浮力

将式(2)和式(3)代入式(1)的过程中，注意应力符号约定的学科差异，不妨以压为正，则

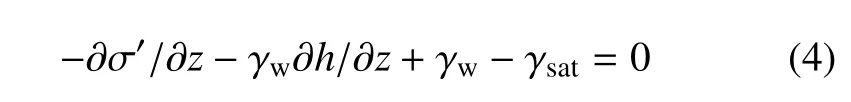
式中，等号左端第3项γw其实就是单位体积饱和土体受到的浮力，它源于位置水头压力在竖向的梯度，在本文中以沿坐标轴正向为正(如果只看其模，就是俗称的孔隙水重度)，而左端第2项则表示渗流的影响.

具体分析还涉及土力学中两个相关概念.

概念1：有1种水力梯度定义

在数学上表示总水头h的梯度对应的负矢量，反映驱动孔隙水渗流的一种作用.

概念2：根据三相关系，饱和土体有效重度或浮重度(e ff ective or buoyant unit weight)[13]

按上述两概念，改写式(4)，得到式(1)的等价形式

式中，若γwi和−γ′数值为正,则表示沿坐标轴正向.

可见，单位体积的浮力与总体力 fz都是矢量，两者合并成单位体积有效体力，记.也就是说，饱和土的浮力被整合到有效体力或通常的浮重度概念中，这较易理解.

2.2 骨架平衡微分方程与渗透力

接下来的问题是：渗透力在哪里？

需要先回到土力学界对渗透力的常规理解.不妨以国外近期和较早的著作为例.Das[14]认为：“Flow ofwaterthroughasoilmassresultsinsomeforcebeingexerted on the soil itself”.Budhu[13]认为：“As water fl ows through soil,it exerts a frictional drag on the soil particles,resulting in head losses.The frictional drag is called seepage force in soil mechanics”.Lambe 等[15]认为：“The seepage force is applied by the moving water to the soil skeleton through frictional drag”.可见，渗透力定义至少有两个要求：孔隙水渗流；对土体或骨架能产生某种作用.

分析式(7)可知，该式左端第2项，刚好能满足这两个条件，所以有理由将其定义为一种渗透力

它反映了渗流场对有效应力场的耦合作用.

事实上，式(8)就是传统土力学最常见的渗透力表述或推导结果.本文从骨架受力平衡角度，提供了考察渗透力和浮力的不同于传统孔隙水隔离体法的新视角，也可作为推导渗透力方法的新补充.这种方法不失简洁和意义深刻.

利用式(8)，可使式(7)的数学表述更简洁

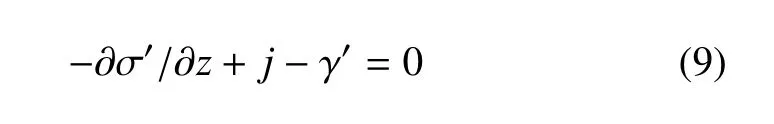
式中，单位体积土体浮力γw与饱和体力 fz合并成−γ′，即

若土体孔隙中无水，则有 j= 0，γw= 0，γsat= γ′= γd(干重度)，此时式 (9)退化为弹性力学一维平衡微分方程 (按弹力符号约定)式 (1)，即∂σ/∂z+fz=0，此时 σ = σ′，fz= −γd，这表示干土的静力平衡.

3 孔隙水平衡微分方程与渗透力和浮力

3.1 孔隙水平衡微分方程与浮力

经典土力学中的孔隙水隔离体法[19]主要是借助一定宏观尺寸的力学模型进行分析，而很少采用连续介质力学中局部化形式的平衡微分方程法.

采用土力学应力符号约定，总应力平衡微分方程式(1)改写为

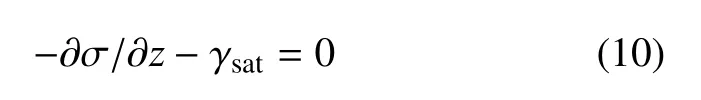
将总应力平衡微分方程(10)减去骨架平衡微分方程式(9)，得到

将有效应力方程式(2)代入式(11)，得到

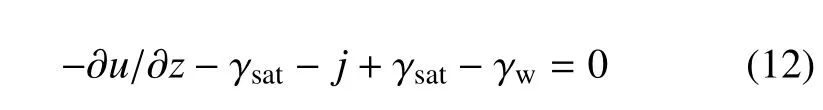
等价简化式(12)，得到孔隙水平衡微分方程为

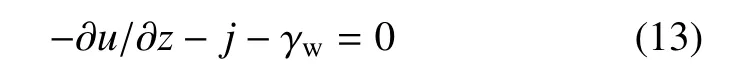
式中，等号左端第3项和第2项分别表示土体受到的浮力反力以及渗透力反力作用.−γw和−j的数值为负值，表示反力方向沿坐标轴负向.

当土体中无渗流时，孔隙水成为静水，一般应有j=0.此时，式(13)就简化为流体力学中一维的欧拉方程，即均匀重力场中静止流体的一维平衡方程.

若在一维欧拉方程中进一步忽略浮力即不计重力场对孔隙水的作用，则式(13)退化为∂u/∂z=0，此时孔隙水压力u等于与坐标无关的某个常数.这意味着孔压在流体中每一点都相同；对于密闭流体而言，此即帕斯卡的静压传递原理.

3.2 孔隙水平衡微分方程与渗透力

现假定渗透力 j未知，则根据孔隙水平衡方程式(13)，可推导出 j的具体表达式

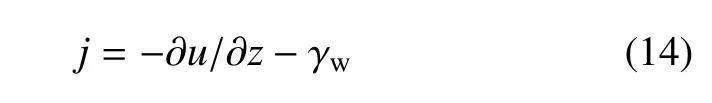
再依据孔隙水压力方程式(3)，得到渗透力为

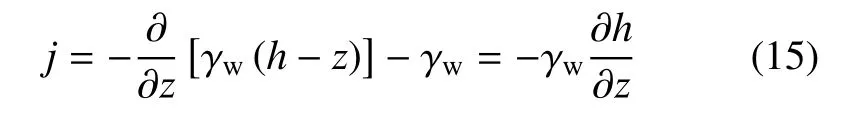
若同样采用式(5)的水力梯度定义，则式(15)就完全等价于式(8)，即 j=γwi.

这样就按主流的孔隙水隔离体法思想实现了对渗透力的新推导.

重点分析以下3点：(1)结果对比表明，无论采用骨架平衡式(7)还是孔隙水平衡方程式(13)，都可以非常一致地推出渗透力 j的表达式(8)；而传统土力学研究中通常忽略了基于骨架平衡的分析方法，这似乎是不够理性和全面的.(2)对比式(13)与式(9)，在骨架和孔隙水隔离体平衡微分方程中，浮力γw和渗透力 j前面的符号是相反的：这是相间的作用力和反作用力属性的体现.(3)如果将式(9)和式(13)两端相加，则得到两相整体总应力平衡方程式(10)或式(1)(按弹力应力符号约定)——两式中均不出现渗透力和浮力，因为两者都是固液两相间成对出现的内部作用力.按经典力学观点，如果对系统中所有质点受到的力求和，则内力将相互抵消而仅存外力.对本文的土水整体，外力只包含重力，因而在两相整体平衡方程中外力仅有饱和体力fz(fz=−γsat).

4 应用中的数学等价性

在实际应用中，渗透力和浮力对骨架或固相的作用主要体现在对有效应力的影响方面.现针对一维有效应力计算，采用3种不同算法，简要对比分析在采用/弃用渗透力与浮力概念情况下的计算结果.

4.1 基于渗透力和浮力的有效应力算法

当渗透力 j和浮重力γ′为常数时，式(9)的不定积分结果为

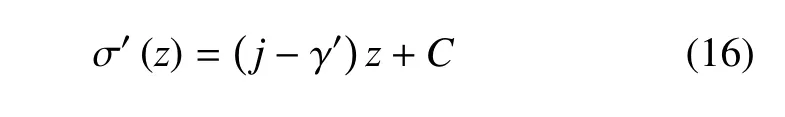
式中，C是积分常数，取决于地表载荷条件.如果设地表 z=H为排水边界、地表边界处有效应力σ′(H)=q以及孔压为u(H)=uH，则式(9)的定积分结果即有效应力分布为

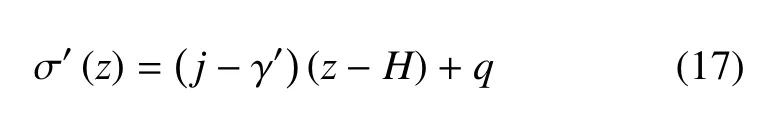
有些土力学著作[16]给出的不同方向渗流作用下有效应力的计算公式，其实都可以统一成式(17).

然而，当渗透力 j随坐标z变化，式(16)和式(17)将不再适用.这体现了传统渗透力和浮力算法的适用范围.

4.2 基于总水头和浮力的有效应力算法

考虑 j为变数而γ′仍为常数的情况，此时无法直接对j按常量积分，但可根据式(4)求出被积函数∂σ′/∂z的不定积分

式中，D是积分常数，依赖于地表载荷情况.引入上述边界条件后的定积分结果为

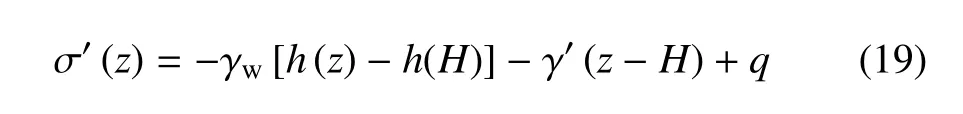
有效应力分布式(18)和式(19)具有更普遍的意义.当渗透力j为常数时，两者分别能够退化为基于j的有效应力函数式(16)和式(17).此时两种算法在数学上是等价变换.然而，式(18)和式(19)根本不涉及渗透力，而主要取决于总水头函数h(z)和有效体力 −γ′.

这初步表明，在进行有效应力计算时，渗透力并非不可或缺的中间量；个别情况下，渗透力算法的式(16)和式(17)反而会缩小问题的求解范围.

4.3 基于3个基本方程直接积分的有效应力算法

对同一定解问题和边界条件，此处按式(1)～式(3)进行求解，而不用从渗透力和浮力概念出发.

对总应力平衡方程式(1)进行不定积分，并按土力学应力习惯用法有

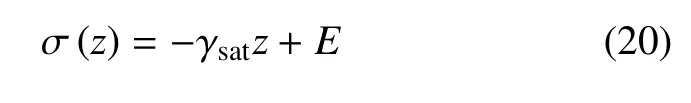
式中，E为积分常数.引入同样的边界条件，得到总应力的定积分

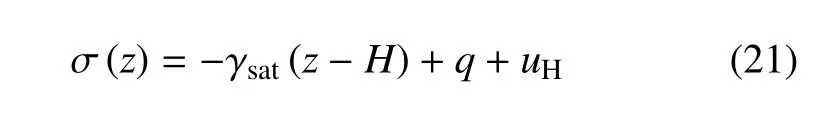
根据有效应力方程式(2)，得到有效应力

将式(21)和孔压方程式(3)代入式(22)，同样能得到有效应力沿埋深的分布函数σ′(z).该结果与式(19)完全相同(具体过程从略).

鉴于上述论证，不妨据此推论：作为控制土体强度和变形的有效应力，其实不必根据额外考虑渗透力和浮力的特殊方程来推导.

然而，渗透力和浮力在理论与工程中毕竟得到了一定的普及和应用.在实际应用中，偏执于对渗透力和浮力概念绝对肯定或否定的任一极端观点可能都未必明智.应意识到使用渗透力和浮力尤其是前者必然带来的局限性.

5 讨论

5.1 传统土力学对渗透力的机理解释准确吗？

李广信[4]认为渗透力是渗透水流对土骨架中的颗粒的推动力和拖曳力，并从土颗粒某种受力分析出发，推导出渗透力的计算公式，即本文式(8).钱家欢等[8]仅将渗透水流施于单位土体内土粒上的拖曳力称为渗透力，这与Lambe等[15]的观点基本一致，同样得到本文式(8).

对机理的深入研究是有益的，但基于不同机理解释得到同样的渗透力表达结果，却很难理解：如果渗透力结果与机理解释的差别无关，那么已有的某些机理解释是否准确和合理？值得思考.

5.2 传统土力学的渗透力需要修正吗？

2004年，Li和Ming[17]提出渗透力的另一不同表达

式中，n是土体孔隙率.

2014年，邵龙潭等[7]也提出了与式(23)基本一样的研究结果，并给出了更详细的论证过程，认为传统土力学得到的渗透力式(8)是错误的，需要按式(23)进行修正.2016年，李广信在渗透力有关的文章[4]和著作中均没有提到和评价文献[7,17]的这些不同观点与建议.

因此，传统土力学中渗透力式(8)是否需要修正，如果需要修正，又该如何完善？

5.3 既有推导方法充分利用有效应力方程了吗？

2015年，陈愈炯[18]报道了自 1954年以来，Terzaghi有效应力原理在我国的应用历史和部分实例，并“鼓励同仁们重视该原理的应用，在应用过程中提高自己的洞察力和处理工程问题的能力，从而取得意想不到的好效果”.

纵观国内外主要的土力学著作，笔者尚未发现有明确利用Terzaghi有效应力原理或方程来完整推导渗透力的相关论述.在论文中，蒋中明等[6]使用Terzaghi有效应力方程，按张量方法进行了多维渗透力推导，但未就最终结果进行深入讨论.

本文将Terzaghi有效应力方程作为基本方程之一进行渗透力的推导，是应用有效应力原理或方程的有益尝试.使人“意想不到”的是，本文方法有助于避开渗透力具体物理意义或机理解释方面的矛盾和争议，将传统土力学渗透力的本质阐释主要归于Terzaghi有效应力原理与方程内在的基础理论前提.

有趣的是，1996年，Terzaghi等[19]认为，“although no theoretical basis for Eq.15.2(即本文式(2).——笔者注)has been found,its empirical basis is so well established that a quantitative knowledge for the interparticle reactions is not needed”.按该观点，理论基础的缺失并不影响Terzaghi有效应力方程的实用性，因为经验性基础可以取代对粒间反力的定量知识.在该意义上，传统渗透力式(8)也应视为经验性的Terzaghi有效应力方程联合其他基本方程的一个具体应用.

以下对比蒋中明等[6]对有效应力方程的应用情况.按其推导思想，在总应力平衡方程中，利用σ=σ+χu−χu(χ为任一实数)数学恒等式以及饱和土物理指标关系：γsat= γd+nγw(γd是土体干重度)，同时考虑本文其他两个基本方程，可以推导出以下一维平衡微分方程

当χ=n时，式(24)退化为

式(25)对应于文献[6]在竖直方向渗流的一维结果(符号约定稍有不同).式(25)等号左端第4项就是式(23)给出的渗透力新定义形式.但这是渗透力吗？

按文献[6]，式(25)左端第3项被“规定定义”为浮力，理由是“重力方向的压力差或压力梯度就是浮力”；第4项nγwi被规定定义为“代表拖曳力”；而渗透力被诠释为由式(25)等号左端最后两项共同构成，容易得到，式(25)左端最后两项的和

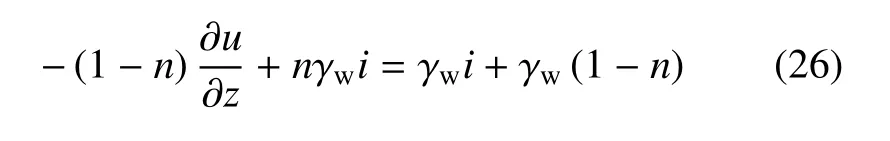
显然，式(26)的结果并不仅受渗流的影响，将“浮力”与“拖曳力”之和定义为“渗透力”值得商榷.

此外，文献[6]的“浮力”定义对于静水压力状态才成立；因为此时重力势和孔压势梯度之和为零，所以也可以用重力势梯度来表述.但对于一般的渗流状态，将总孔压梯度作为浮力是不合适的，因为此时∂u/∂z受渗流影响是变数.这意味着单位体积的“浮力”不是常数.所以，这种分析方法似乎没有充分阐明和区分浮力和渗透力的准确内涵，也不能作为式(23)具有合理性的证明.

如果将变换后平衡方程中出现的任一γwi有关项，都称为渗透力，如式(24)中的χγwi，似乎也是不合适的，因为χ是任一实数.在骨架平衡方程中，当且仅当γwi有关项全部反映渗流的影响时，将其归为渗透力才是合理的.而骨架平衡方程式(24)和(25)中∂u/∂z其实仍然与渗流相关.

容易看出，式(25)与式(9)或式(7)实际上完全等价，而且都采用了Terzaghi有效应力方程.

5.4 渗透力新定义式(23)还有其他解读方法吗？

这里将详细论述一种证明式(23)的可能方法.

前述3个基本方程中，用Biot有效应力方程[20]

替代Terzaghi有效应力方程式(2)，按同样思路和推导即分别得到骨架和孔隙水平衡方程的另一形式

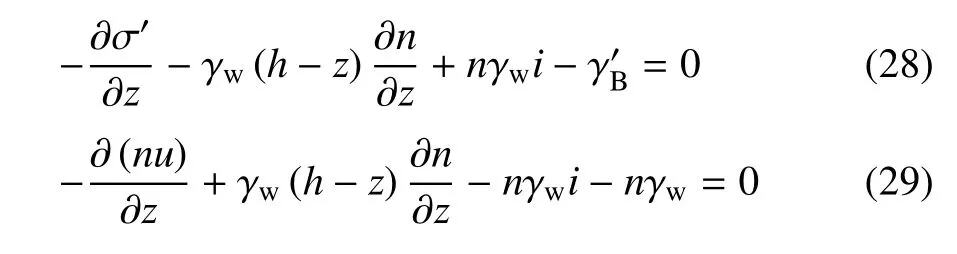
当孔隙率n随埋深不变或其梯度为零时，式(28)和式(29)分别简化为

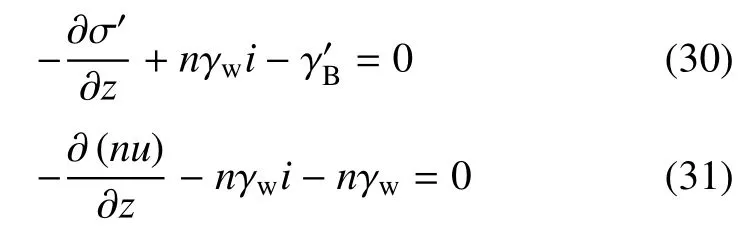
对比式(30)与骨架平衡微分方程式(9)可知，只有式(30)等号左端第2项与渗流有关.所以，形式上nγwi也同样符合渗透力定义的两种条件，即式(23)可称为一种渗透力，这在形式上可以得到论证.

尽管文献[7,17]并没有阐明采用Biot有效应力方程式(27)，但根据上述分析，异于传统的渗透力式(23)隐含了Biot有效应力方程，而其他有效应力方程无法在形式上得到式(23)的结果.

5.5 渗透力新定义式(23)的应用会带来哪些变化？

渗透力的传统表述式(8)与新定义式(23)明显不同.新渗透力式(23)若要得到岩土工程界的普遍接受，除了最终需要工程实践检验之外，还应事先在理论上体现其不同以往的特点或优点.

因此就有必要对本文基本方程之一的有效应力方程加以讨论.如前所述，两种渗透力结果差异的主要原因是分别采用了Terzaghi有效应力方程式(2)和Biot有效应力方程式(27).对同一问题而言，总应力σ和孔隙水压u相对客观，而有效应力无法直接测量，因而可以按无量纲方法分析不同有效应力方程对应的无量纲有效应力的差异性规律，见图2.其中，式 (2)对应于 σ′/σ =1−u/σ，而式 (27)对应于σ′/σ =1−nu/σ.

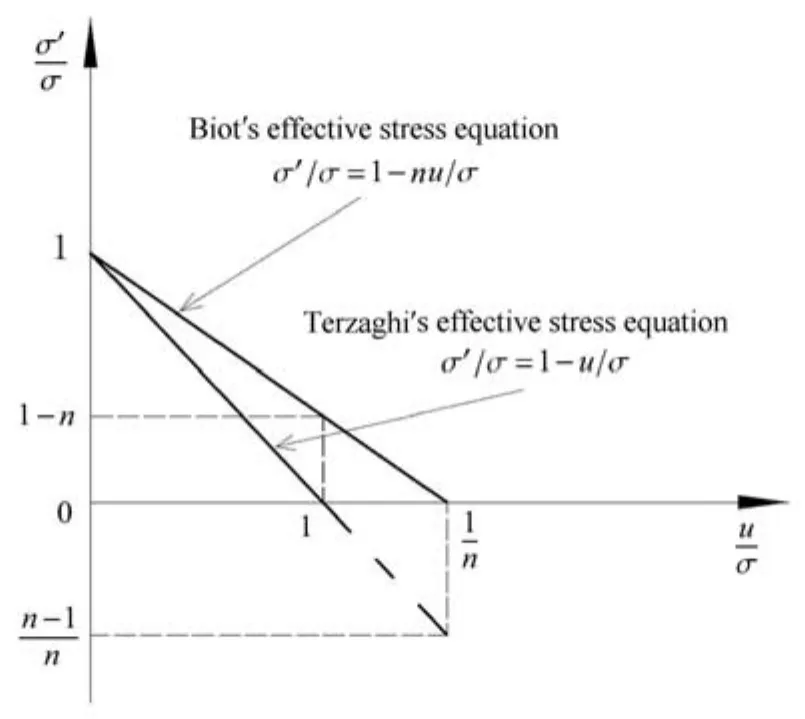
图2 Biot和Terzaghi两种有效应力方程的无量纲形式Fig.2 Dimensionless forms of e ff ective stress equations given by Biot and Terzaghi,respectively

分析图2可知，只有在无量纲孔压u/σ为零时，两种无量纲有效应力σ′/σ结果才相同.随着u/σ的增大，两者差别逐渐显著，其中 σ′/σ的 Biot理论值总是大于u/σ相同情况下的Terzaghi理论值.当u/σ =1时，按 Terzaghi理论得到的 σ′/σ 为零，这符合通常的理解和认识，而且常用作发生流土或砂沸的临界判别条件.但此时若按Biot理论，则有σ′/σ=1−n＞0，不会发生流土.

而当基于 Biot有效应力方程的无量纲有效应力 σ′/σ =0时，则要求对应的无量纲孔压 u/σ =1/n＞1.此时相应的Terzaghi有效应力是负值，即σ′/σ=(n−1)/n＜0.这对经典土力学观点而言，将出现比较奇怪的现象:对于不能承受拉应力的土体，此时早已发生破坏而可能不存在该状态.所以，在相同的总应力和孔压条件下，相比Terzaghi有效应力方程，在判断流土现象时，基于Biot有效应力方程的结果在理论上偏于不安全.

进一步看，出现流土的临界力学条件一般为σ′=0.按本文式(17)，在均质土层的表面载荷q=0条件下，当渗透力 j=γwi=γ′时，土层中任意点σ′(z)≡0，由此推导出通常的临界水力梯度

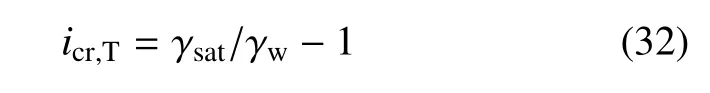
因此，有

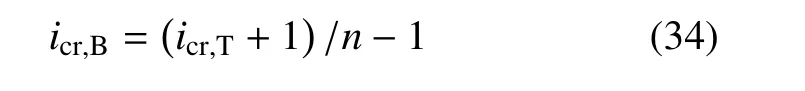
在实际工程中,土体平均孔隙率有一定的变化范围[21]，对常见砂土 n一般为 0.29～0.44，而对通常黏性土n为0.29～0.52.再根据传统的临界水力梯度icr,T值[14]大多介于0.85和1.1之间的经验，以及式(34)，就可以得到icr,B对应的大致变化范围为2.6～6.2.

因此，icr,B/icr,T在2.4～7.3之间，相对于传统土力学中的经验结果，基于常见土体参数统计规律的临界水力梯度经验值将偏大很多.可见，渗透力新定义式(23)及其对应的icr,B用于流土(砂)可能性的破坏评价时，是非常不安全的.

再结合张邦芾[22]近两年的基坑渗流试验结果予以验证.在该试验中，4组试验细砂土样平均孔隙率 n为 0.48～ 0.49，饱和重度 γsat为 18.21～18.05kN/m3，传统的临界水力梯度值icr,T为0.858～0.842.4种工况的坑内止水帷幕插入深度范围内平均水力梯度i为1.013～1.153,大于icr,T；试验最终观察到各工况均发生流土破坏.按传统渗透力定义式(8)和对应临界水力梯度式(32)可以较好地评估此类渗透破坏.

而如果按渗透力新定义式 (23)及对应的临界水力梯度式(33)，发生流土的临界水力梯度icr,B为2.867～2.755.因为i＜icr,B，所以试样理论上应处于稳定状态，但实际试验中却发生了流土破坏.这表明渗透力新定义及对应临界水力梯度在这种情况下是不适用的，将其普遍用于指导工程实践的安全风险可能很高.

5.6 其他

此外，当地表载荷q≠0时，传统流土临界条件j=γ′将不再适用，因为按式(17)有σ′(z)≡q≠0.这也反映了传统渗透力概念在应用中的局限性，此时判别流土临界状态，也可以不采用渗透力概念而直接按有效应力来处理.

笔者还注意到，1958年，苏联学者格尔西万诺夫和包利兴[2]在研究地下水层流上升时的现象时，采用了如下方程

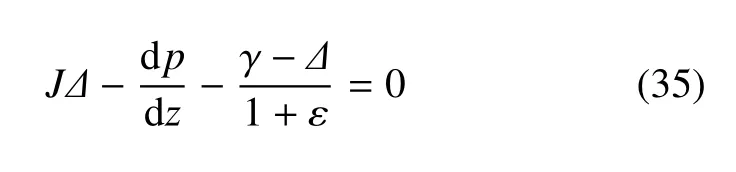
该方程与式(9)有些相似，但文献[2]既没有阐明该式的由来，也没有提到本文的3个基本方程，而且还将式(35)等号左端最后1项阐明为干容重(干重度).按式(9)来看，这可能是错误的，应该为浮重度.

在推导渗透力(动水压力)时，文献[2]并不是从式(35)出发，而是根据前述宏观尺寸的孔隙水隔离体法，在考虑孔隙水惯性力的影响下得到渗透力表达式

式中，q是渗流速度，在文献[2]中写为g可能是刊误.式(36)等号右端第2项反映孔隙水惯性力影响.

笔者基于已有的固结理论方面的成果[10]，在忽略骨架速度和加速度的前提下[23]，探讨并提出一种能够考虑液相速度和加速度的广义多维渗透力

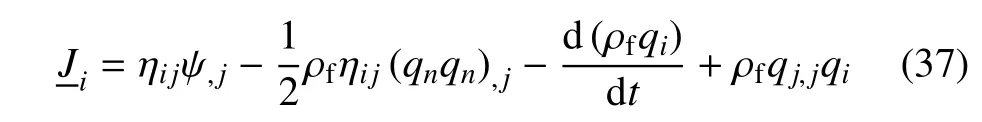
如果在式(37)中引入以下简化假设：(1)Terzaghi有效应力方程成立ηij=δij；(2)一维问题假定i=j=z；(3)孔隙流体为孔隙水ρf=ρw，则式(37)严格退化为

不难发现，化简后的多维广义渗透力式(38)与式(36)等价，即这样，初步证明了格尔西万诺夫和包利兴提出的一维渗透力式(36)在理论上依然是严谨的，同时也揭示了其渗透力推导方法中同样隐含使用了Terzaghi有效应力方程，而其他有效应力方程无法导出式(36).

值得关注的还有，国内学者雷国辉等[2425]还研究了渗透力在瑞典条分法边坡稳定分析中应用的注意事项与局限性，并提出作用在骨架上的渗透力并非体积力的观点等.但是，Pan等[26]在三维边坡稳定分析中，却将渗透力视为作用于离散单元上的体积力进行数值计算.另外，Al-Madhhachi等[27]在黏性土侵蚀率模型中考虑了渗透力概念以改进经典Wilson模型的预测精度.这些研究中采用的渗透力主要是式(8)的传统形式，而没有使用更精确的式(36)或式(38).这表明，在工程实践中，亟待加强渗透力的理论和应用研究.

6 结论

(1)针对一维工况，明确了分析饱和土渗透力和浮力的3个基本方程，由此分别得到骨架平衡微分方程式(9)和孔隙水隔离体平衡微分方程式(13).这两种方法和思路都能够准确而不失简洁地推导出渗透力和浮力.传统和主流的宏观尺度孔隙水隔离体法不再是分析渗透力和浮力的唯一方法.

(2)土中无水时，骨架平衡微分方程式(9)可以退化为弹性力学平衡微分方程(干土).不考虑渗透力(和浮力)时，孔隙水平衡微分方程(13)可以退化为流体力学欧拉方程(和帕斯卡静压传递方程).

(3)一维渗流问题中的有效应力计算，在简单情况下可以按渗透力和浮力分析即式(17).但一般情况下可以直接按本文3个基本方程求解即式(19)，此时无需利用渗透力等概念.

(4)对最新渗透力研究成果的讨论工作表明：①证明传统渗透力式(8)存在合理性的关键因素是充分和正确地应用3个基本方程中的Terzaghi有效应力方程；②从Biot有效应力方程及本文其他2个基本方程来看，其他学者提出的渗透力新定义j=nγwi在形式上是合理的，但从有限的工程实践经验和试验成果来分析，该新定义若用于流土破坏评估等工程问题则可能是很不安全的，值得注意和警惕.

(5)格尔西万诺夫和包利兴提出的渗透力定义式(36)，在Terzaghi有效应力方程和一维问题范畴内是严谨成立的，仍不过时.

致谢感谢匿名审稿专家给本文提出的宝贵指导意见；科学出版社工程技术分社张晓娟编辑和北京交通大学土建学院李舰博士协助进行本文标点符号和个别语言的修改完善；北京交通大学陈曦教授对摘要的英文翻译加以润色和改进；研究生王思远将图1和图2改绘为AUTOCAD格式.谨此致谢.

1弗洛林BA.土力学原理(第1卷).同济大学土力学及地基基础教研室，译.北京:中国工业出版社,1965(Φлoрин BA.Fundamentals of Sol Mechanics(Vol.1).The Faculty of Soil Mechanics and Foundation Engineering of Tongji Univerisity,transl.Beijing:China Industry Press,1965(in Chinese))

2格尔西万诺夫HM,包利兴ДE.土力学的理论原理及其实际应用.魏汝龙，译.北京:建筑工程出版社出版,1958(Γeрсeвaнoв HM,Πoльшин ДE.Theoretical Principles of Soil Mechanics with Its Practical Applications.Wei Rulong,transl.Beijing:China Architecture&Building Press,1958(in Chinese))

3 Terzaghi,K.Theoretical Soil Mechanics.New York:John Wiley and Sons,Inc.,1943

4李广信.论土骨架与渗透力.岩土工程学报,2016,38(8):1522-1528(Li Guangxin.On soil skeleton and seepage force.Chinese Journal of Geotechnical Engineering,2016,38(8):1522-1528(in Chinese))

5祝恩阳.考虑孔隙水浮力的渗透力公式推导.力学与实践,2015,37(6):761-762(Zhu Enyang.Derivation of the seepage force.Mechanics in Engineering,2015,37(6):761-762(in Chinese))

6蒋中明,龙芳，熊小虎等.边坡稳定性分析中的渗透力计算方法考证.岩土力学,2015,36(9):2478-2486,2493(Jiang Zhongming,Long Fang,Xiong Xiaohu,et al.Study of calculation methods of acting force of seepage in slope stability analysis.Rock and Soil Mechanics,2015,36(9):2478-2486,2493(in Chinese))

7邵龙潭,郭晓霞.有效应力新解.北京:中国水利水电出版社,2014(Shao Longtan,Guo Xiaoxia.Interpretation of E ff ective Stress.Beijing:China Water&Power Press,2014(in Chinese))

8钱家欢.土力学.南京:河海大学出版社,1988(Qian Jiaohuan.Soil Mechanics.Nanjing:Hehai University Press,1988(in Chinese))

9陈仲颐,周景星,王洪瑾.土力学.北京:清华大学出版社,1994(Chen Zhongyi,Zhou Jingxing,Wang Hongjin.Soil Mechanics.Beijing:Tsinghua University Press,1994(in Chinese))

10丁洲祥，龚晓南，谢永利.欧拉描述的大变形固结理论.力学学报,2005,37(1):92-99(Ding Zhouxiang,Gong Xiaonan,Xie Yongli.Finite strain consolidation theory with eulerian description.Acta Mechanica Sinica,2005,37(1):92-99(in Chinese))

11 Timoshenko S,Goodier JN.Theory of Elasticity. New York:McGraw-Hill Book Company,Inc.,1951

12 Gerhart PM,Gerhart AL,Hochstein JI.Munson,Young and Okiishi’s Fundamentals of Fluid Mechanics,8th ed.New York:John Wiley&Sons,2016

13 Budhu M.Soil Mechanics Fundamentals(Metric Version).Chichester,West Sussex,U.K.:John Wiley&Sons,Ltd.,2015

14 Das BM.Advanced Soil Mechanics,4th ed.Boca Ration:CRC Press,2013

15 Lambe TW,Whitman RV.Soil Mechanics.New York:John Wiley&Sons,1969

16赵成刚,白冰.土力学原理(修订本).北京:清华大学出版社，北京交通大学出版社,2009(Zhao Chenggang,Bai Bing.Principles of Soil Mechanics,Modi fi ed Edition.Beijing:Tsinghua University Press,2009(in Chinese))

17 Li X,Ming H.Seepage driving e ff ect on deformations of San Fernando dams.Soil Dynamics and Earthquake Engineering,2004,24:979-992

18陈愈炯.有效应力原理在中国的应用实例.岩土工程学报,2015,37(9):1674-1677(Chen Yujong.Examples of application of effective stress principle in China.Chinese Journal of Geotechnical Engineering,2015,37(9):1674-1677(in Chinese))

19 Terzaghi,K,Peck RB,Mesri G.Soil Mechanics in Engineering Practice,3rd ed.New York:John Wiley&Sons,Inc.,1996

20 Biot,MA.Theory of elasticity and consolidation for a porous anisotropic solid.Journal of Applied Physics,1955,26(2):182-185

21《工程地质手册》编委会.工程地质手册,第4版.北京:中国建筑工业出版社,2007(Editorial Board of Handbook of Engineering Geology.Handbook of Engineering Geology,4th ed.Beijing:China Architecture&Building Press,2007(in Chinese))

22张邦芾.基坑工程地下水渗流场特性研究.[硕士论文].北京:中国建筑科学研究院,2014(Zhang Bangfu.Study on the characteristics of groundwater seepage fi eld in foundation pit engineering.[Master Thesis].Beijing:China Academy of Building Research,2014(in Chinese))

23丁洲祥.渗透力概念的力学分析及广义化探讨.岩土工程学报,2017,待刊 (Ding Zhouxiang.Mechanical fundamentals of seepage force concept and its generalization.Chinese Journal of Geotechnical Engineering,2017,in Press(in Chinese))

24 Lei GH,Chiu ACF,Ng CWW.Is Terzaghi’s e ff ective stress a stress variable under seepage conditions.Journal of Central South University,2015,22:2316-2321

25雷国辉，郑强.瑞典条分法剖析引发的有效应力和渗流力概念问题.岩土工程学报，2012,34(4):667-676(Lei Guohui,Zheng Qiang.Issues on concepts of e ff ective stress and seepage force arising from anatomizing Swedish slice method.Chinese Journal of Geotechnical Engineering,2012,34(4):667-676(in Chinese))

26 Pan Q,Xu J,Dias D.Three-dimensional stability of a slope subjected to seepage force.International Journal of Geomechanics,2017,17(8):04017035,1-9

27 Al-Madhhachi AT,Fox GA,Hanson GJ,et al.Mechanistic detachment rate model to predict soil erodibility due to fl uvial and seepage force.Journal of Hydraulic Engineering,2014,140(5):04014010,1-12

ONE-DIMENSIONAL SEEPAGE FORCE AND BUOYANCY1)

Ding Zhouxiang∗,†,2)∗(School of Civil Engineering，Beijing Jiaotong University，Beijing 100044，China)
†(Shaanxi Provincial Major Laboratory for Highway Bridge&Tunnel，Xi’an 710064，China)

Forthesakeofsimplicity,twomethodsofderivingseepageforceandbuoyancyassociatedwithone-dimensional fl uid fl ow in saturated soil were developed to give a uselful supplement to conventional macro-scale method of isolated pore fl uid.To study the seepage force and buoyancy,three fundamental governing equations,namely,equilibrium di ff erential equation in elasticity,Terzaghi’s e ff ective stress equation and simpli fi ed Bernoulli’s equation in fl uid mechanics,are utilized for the derivation of seepage force and buoyancy.Based on the fundamental governing equations,it is readily to derive the di ff erential equations of equilibrium corresponding to the isolated soil skeleton and the isolated pore fl uid,and hence,the connotation and nature of seepage force and buoyancy can be disclosed.The seepage force per unit volume of saturated soil arises from the gradient of fl uid pressure in terms of total head.The buoyancy originates in the vertical component of gradient of fl uid pressure in terms of position head.Both the seepage force and the buoyancy can be embodied in equilibirium di ff erential equation with respect to skeleton or pore fl uid of satured soil.In geotechnical practice,the three governing equations can be directly applied to the calculation of e ff ective stress.Only in some simpli fi ed cases,the distribution of e ff ective stress can be obtained using the seepage force and buoyancy.Additionally,some hot topics are also discussed in this study,and emphasis shall be put on the discussion on the rationality and the potential application risk of the new de fi nition of seepage force,i.e.,j=nγwi.The strictness of one classic formulation of seepage force in history was thoroughly validated when considering the derivative of seepage velocity with respect to time.It is noteworthy that in the study of seepage force and buoyance from the perspective of soil mechanics,the Terzaghi’s e ff ective stress equation shall be reasonably implemented with practical signi fi cance.

seepage force，buoyancy,e ff ective stress principle,pore water pressure,di ff erential equilibrium equation.

TU431

A

10.6052/0459-1879-17-001

2017–01–01收稿，2017–06–08 录用,2017–06–22 网络版发表.

1)国家自然科学基金(51278028,41172221)和中央高校基本科研业务费专项资金(310821161119,2014JBM087)资助项目.

2)丁洲祥，博士，副教授，主要研究方向：固结理论及其在岩土和隧道工程中的应用.E-mail:dingzhouxiang@163.com

丁洲祥.一维渗透力与浮力.力学学报，2017，49(5):1154-1162

Ding Zhouxiang.One-dimensional seepage force and bouyancy.Chinese Journal of Theoretical and Applied Mechanics,2017,49(5):1154-1162