多体系统接触碰撞问题的牛顿--欧拉线性互补方法1)

富 立 胡鸿奎 富 腾

(华北理工大学理学院，河北唐山063210)

多体系统接触碰撞问题的牛顿
--欧拉线性互补方法1)

富 立2)胡鸿奎 富 腾

(华北理工大学理学院，河北唐山063210)

基于非光滑动力学方法的多体系统接触碰撞分析是目前多体系统动力学的研究热点.本文采用牛顿--欧拉方法建立多体系统接触、碰撞问题的动力学模型，给出一种牛顿--欧拉型线性互补公式.该建模方法与目前一般采用的拉格朗日建模方法的不同之处是约束条件中除了库仑摩擦、单边约束之外还含有光滑等式约束.在建立系统动力学模型时，首先解除摩擦约束和单边约束得到原系统对应的基本系统.牛顿--欧拉方法采用最大数目坐标建立基本系统的动力学方程，由于坐标不相互独立，因此基本系统中带有等式约束，其数学模型为一组微分代数方程.借助约束雅可比矩阵,在基本系统微分代数方程中添加摩擦接触和单边约束对应的拉氏乘子,就可以得到系统全局运动的具有变拓扑结构特征的动力学方程，再结合非光滑约束互补条件便可构成完备的系统动力学模型.完备的动力学模型由动力学微分方程以及等式约束和不等式约束组成.线性互补公式采用分块矩阵形式进行推导，简化了推导过程.数值计算采用基于线性互补的时间步进算法.时间步进算法是目前流行的非光滑数值算法，其突出特点是可以免去数值积分中繁琐的事件检测过程,而数值积分过程中通过对线性互补问题的求解可以确定系统的触--离状态.通过对典型的曲柄滑块间隙机构进行数值分析，验证本文方法的有效性.

非光滑，多体系统，摩擦，碰撞，线性互补问题

引言

近三十年来，非光滑多体系统动力学在基础理论以及数值算法等方面取得显著进展并成为力学研究的热门领域之一.20世纪80年代，Moreau[1]将凸分析理论与测度微分包含理论相结合，应用于求解含摩擦、碰撞的刚体动力学问题，奠定了现代非光滑力学的数学和力学基础.Panagiotopoulos[2]引入非凸变分不等式，进一步发展和完善了现代非光滑力学理论.数值算法方面，非光滑多体系统问题的关键是对滞-滑转换,触-离转换以及碰撞等事件的检测问题.随着约束数目的增加，事件检测所需的计算量呈指数速率迅速增长，这是所谓的Delassus问题[3].为克服这一难题，目前流行的做法是采用线性互补方法[4].L¨otstedt[5]首次将刚体的接触问题归结为一个含线性互补条件的数学规划问题来处理,此后,经Bara ff等学者们[611]的努力，将这一理论框架成功地应用于多体系统动力学理论之中.

近几年来，非光滑多体系统动力学有以下研究热点及进展.在基础理论方面,解的存在与唯一性、碰撞本构关系、动力学建模等问题的研究取得进展.文献[12]论证了存在或不存在库仑摩擦情况下单、双边约束多体系统解的存在与唯一性问题.文献[13]对经典的Painlev´e问题给出新的分析方法和结果.文献[14-15]研究碰撞定律的能量协调条件以及基于能量恢复系数的建模方法.数值算法方面：在时间步进算法、并行算法以及单边约束违约修正算法等方面取得进展.文献[16-17]分别研究了消除约束漂移效应的迭代投影时间步进算法和提高计算精度的半显式时间步进算法.文献[18]将Baumgarte稳定化方法推广至含二维摩擦的多体动力学问题.文献[19-20]给出对非光滑事件进行有效检测的数值算法.在应用研究方面,已有的非光滑多体系统动力学理论成果被应用于航空航天、机械、机器人、车辆、生物力学、天文学等诸多领域.如小行星聚集的接触动力学[2122]，航天器空间对接动力学[23]，间隙机构动力学[2425]，颗粒物质动力学[26]，危岩崩塌轨迹的数值模拟[27]、机器人动力学[28]、人体步态分析[29[31]、车辆非光滑动力学建模与数值模拟[32]等.

经典多体系统动力学的建模方法主要有两类[4,2931].一类是拉格朗日方法或凯恩方法，该方法选取最少数目的独立广义坐标，系统运动由一组常微分方程来描述；另一类是牛顿--欧拉方法，该方法选取最大数目的非独立广义坐标，系统运动由一组微分代数方程来描述.P ff ei ff e等提出的非光滑多体系统动力学公式采用拉格朗日方法建立基本系统的动力学方程，其数学模型为一组常微分方程.利用单边约束雅可比矩阵，在基本系统动力学方程中添加接触力及碰撞力进一步可得到多体系统摩擦、碰撞问题的全局动力学方程.以上方程再结合单边约束以及库仑摩擦约束条件，可推导出基于常微分方程的拉格朗日型非光滑多体系统的线性互补公式.

本文采用牛顿--欧拉方法建立基本系统的动力学方程.与拉格朗日方法不同的是，解除系统单边约束和摩擦接触后，基本系统还存在有光滑等式约束，故基本系统的动力学方程为一组微分代数方程.基本系统微分代数方程结合单边约束以及库仑摩擦接触的约束条件，可得到多体系统摩擦、碰撞问题的牛顿--欧拉型动力模型.

数值计算采用基于线性互补的时间步进算法.首先需建立系统摩擦、碰撞问题的牛顿--欧拉型线性互补公式.将系统动力学方程以及其约束互补条件离散化为差分形式，最终建立速度--冲量形式的线性互补公式.时间步进算法将线性互补解法嵌入至微分代数方程数值积分过程.算法特点是能够求解等式约束与不等式约束并存的非光滑多体系统动力学问题，在数值计算过程中无需对滞--滑状态等非光滑事件进行检测，避免了由事件检测导致的繁复计算.

本文方法是对P ff ei ff e-Glocker方法的进一步推广.建模方面，以牛顿--欧拉方法取代拉格朗日方法，将基本系统的动力学模型由常微分方程扩展为微分代数方程.数值计算采用基于牛顿--欧拉型线性互补公式的时间步进方法.最后通过对典型机构的数值分析验证方法的有效性.

1 多体系统接触碰撞问题的拉格朗日方法

含摩擦、碰撞等因素的非光滑多体系统具有典型的变拓扑结构特征.在运动过程中，系统的约束以及自由度等都是随时间变化的.系统的全局运动可分为自由运动(无单边约束作用)，持续接触(单边约束持续作用)以及碰撞(单边约束瞬间作用)等运动状态.非光滑多体系统动力学理论采用统一的广义坐标来描述系统的全局运动.目前普遍采用的是拉格朗日坐标.采用独立的拉格朗日坐标描述基本系统自由运动的方法，本文称之为拉格朗日方法.

1.1 自由运动阶段

此阶段多体系统没有任何单边约束作用，称为基本系统.设描述基本系统运动的独立拉格朗日坐标是q，并将其作为描述系统全局运动的统一坐标.自由运动的拉格朗日方程为

其中，M是质量矩阵，q是拉格朗日坐标列阵，h为广义力列阵.

1.2 持续接触阶段

此阶段系统受有持续的单边约束作用，采用第一类拉氏方程建立系统的动力学方程并将单边约束表述为互补形式

其中，gN是接触处的法向距离列阵、γT是接触处的切向相对速度列阵，γR和γL是将γT分解后的互补速度，满足关系γT=γR−γL.λN和λT分别是接触处的法向反力列阵和切向摩擦力列阵.λR和λL是将λT分解后的互补摩擦力列阵，满足关系λR=2µλN−λL(µ为摩擦系数矩阵).WN和WT分别是法向和切向的约束雅可比矩阵.在运动过程中，系统的接触状态随时间发生变化，因此方程中的系数矩阵WN和WT以及约束反力列阵λN和λT的维数都是随时间变化的.

1.3 碰撞阶段

设碰撞始于t−终于t+，刚体动力学方法假设碰撞在瞬间完成(∆t=t+−t−→0)，速度产生突变.

碰撞方程以及碰撞互补关系为

其中，ξN和ξT分别是法向和切向的碰撞修正速度，，；ξL和 ξR是将切向修正速度ξT分解后的互补速度，满足关系分别是接触处的法向反力冲量和切向摩擦力冲量；ΛR和ΛL是将ΛT分解后的互补摩擦冲量列阵，满足关系ΛR=2µΛN−ΛL；eN和eT分别是法向、切向碰撞恢复系数对角阵.

1.4 基于线性互补的时间步进算法

在多点接触碰撞问题中，当一点接触状态改变时，如触离状态的改变、滞滑状态的改变或发生碰撞等，都会影响到其他各点的接触状态.在动力学计算中需要对系统的接触状态进行判断.当接触点增多时，这个判断过程是非常繁复的.现代非光滑力学对刚体系统接触状态的判断建立了一种严格而有效的方法，即线性互补方法.该方法将系统动力学方程及其单边约束条件转化为一个线性互补问题，通过求解线性互补问题来判断系统的接触状态，具体参见文献[1,4,7-8]等.

时间步进算法是适于非光滑多体系统的数值积分方法.众多文献所采用的时间步进方法中，Moreau的中点算法是最经典也是使用最广泛的.时间步进方法将动力学方程和单边约束条件离散化，离散化的差分方程不以加速度和力为未知量，而是以速度和冲量取而代之.时间步进算法的突出特点是数值积分过程中无需对非光滑事件进行检测，是真正的非光滑算法.该算法详细内容及主要步骤参见文献[1,11].

2 多体系统接触碰撞问题的牛顿--欧拉方法

2.1 自由运动阶段的牛顿--欧拉方程

本文采用绝对笛卡儿坐标描述基本系统的自由运动，称之为牛顿--欧拉方法.自由运动阶段基本系统没有单边约束只有光滑双边约束，将光滑双边约束的约束反力添加至系统动力学方程(1)中，可以建立用绝对笛卡儿坐标表示的牛顿--欧拉型基本系统动力学方程如下

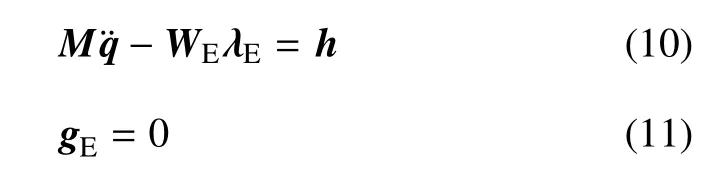
其中，gE是基本系统的光滑双边约束列阵.WE=(∂gE/∂q)T为双边约束的雅可比矩阵的转置矩阵，λE为双边约束的约束力列阵.

2.2 牛顿--欧拉接触动力学方程

持续接触阶段，在方程(2)中添加双边约束的约束反力，并在约束条件(7)～(9)基础上补充光滑双边约束条件gE=0，得到以下持续接触阶段的牛顿--欧拉型系统动力学方程及其约束条件

建立接触阶段线性互补公式时，需要将方程及约束条件(12)～(16)离散化.离散化后的速度--冲量形式的接触动力学模型是

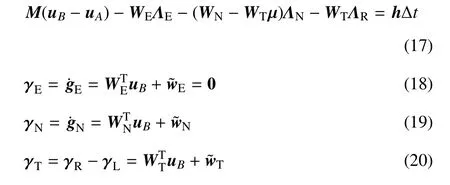
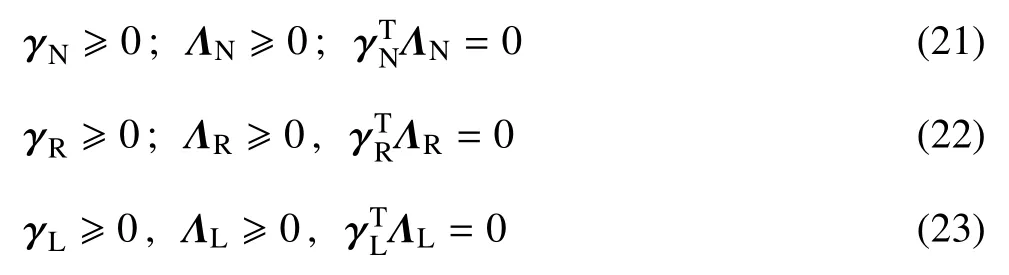
2.3 牛顿--欧拉碰撞动力学方程

在碰撞动力学方程(6)中添加光滑双边约束的约束反力冲量并在碰撞约束条件(7)～(9)中补充光滑双边约束条件，得以下速度--冲量形式的牛顿--欧拉型碰撞动力学模型

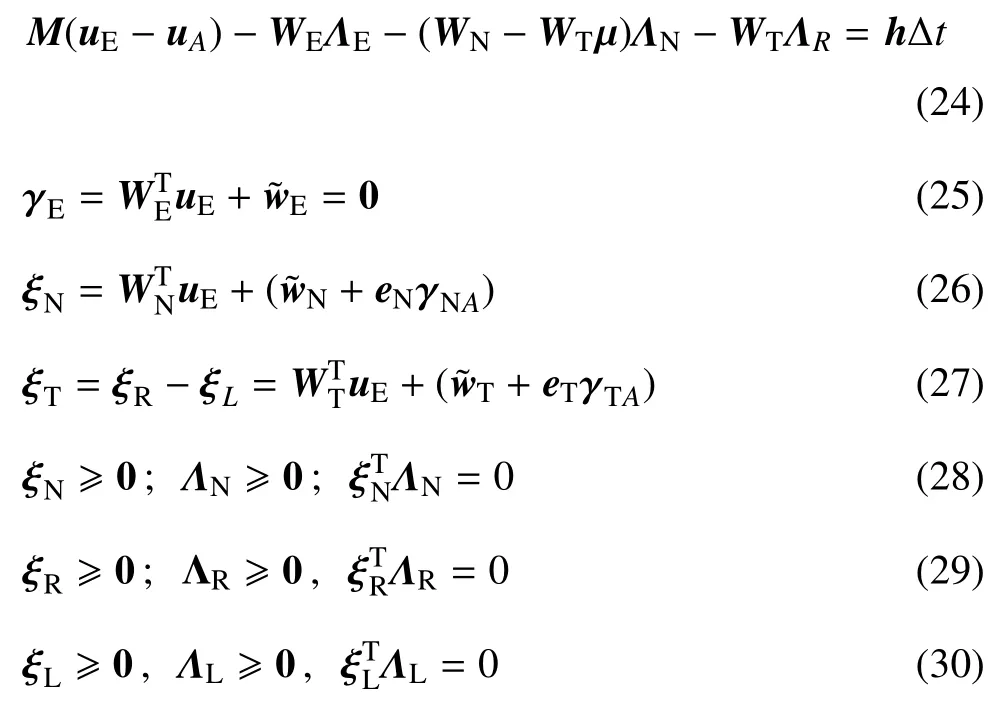
2.4 牛顿--欧拉线性互补公式

接触线性互补公式与碰撞线性互补公式的推导公式类似，以下给出牛顿--欧拉型碰撞线性互补公式.

将式(24)～式(30)，写为矩阵形式

将式(31)写成以下分块矩阵形式

将式(32)展开

由式(33)

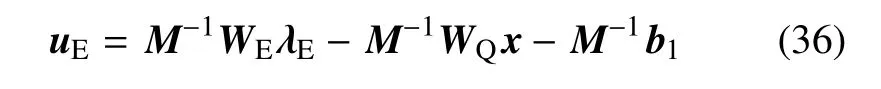
代入式(34)，得

将式(36)代入式(35)，得

将式(37)代入式(38)，得

经整理简化，式(39)简写为

其中

由于x和y之间满足互补关系，因此式(22)最终可化为以下标准线性互补公式

令公式中的恢复系数eN=eT=0，即变为持续接触问题的线性互补公式.

3 算例

含间隙滑移铰曲柄滑块机构如图1所示.其中含间隙的滑移铰如图2所示.

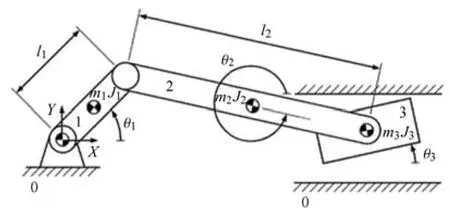
图1 含间隙滑移铰的曲柄滑块机构Fig.1 Slider-crank mechanism with a translational clearance joint

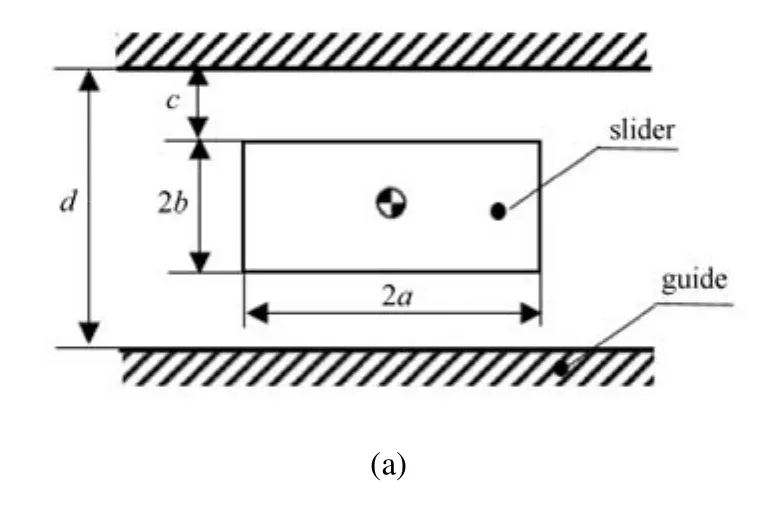
图2 由滑块与滑道轨构成的含间隙滑移铰Fig.2 Translational joint with clearance that is,the slider and guide

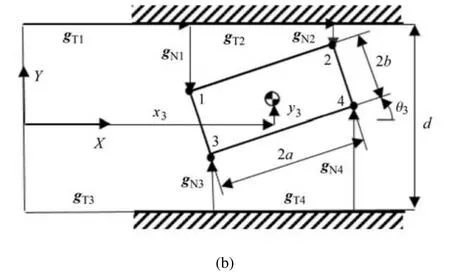
图2 由滑块与滑道轨构成的含间隙滑移铰(续)Fig.2 Translational joint with clearance that is,the slider and guide(continued)

机构几何参数：

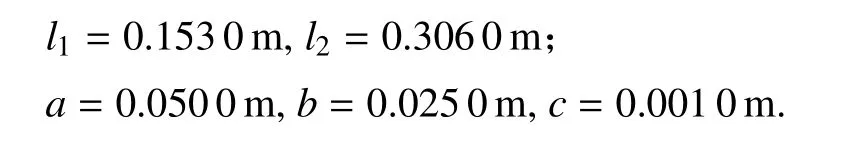
惯性参数：

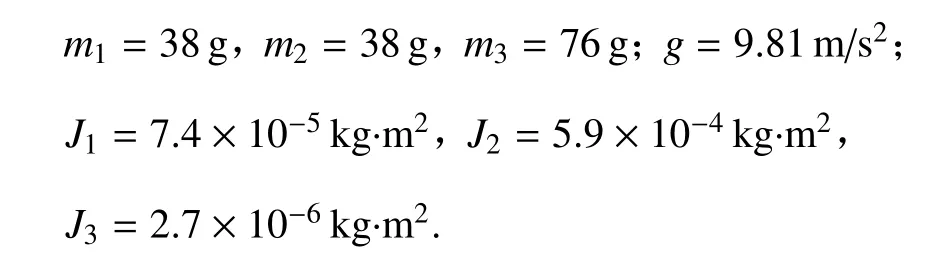
接触参数：

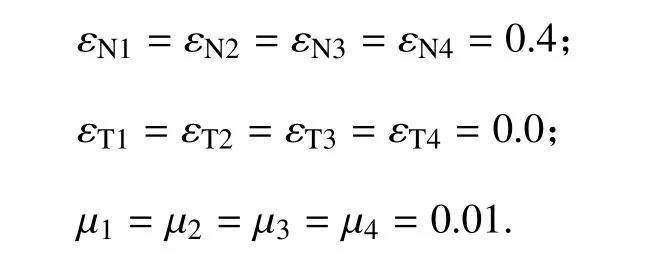
初始条件：

为使问题简化，曲柄和连杆的位形仍然用最少数目坐标，即θ1和θ2，来描述，只有滑块的位形采用最大数目坐标(x3y3θ3)来描述，因此系统的广义坐标为

基本系统动力学方程及其约束

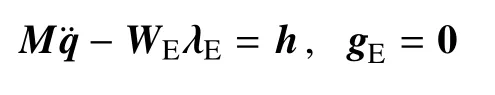
其中

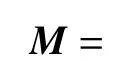
法向和切向约束矩阵为

根据系统的接触状态，WN和WT分别在以下WN1～WN4和WT1～WT4之间取舍组成

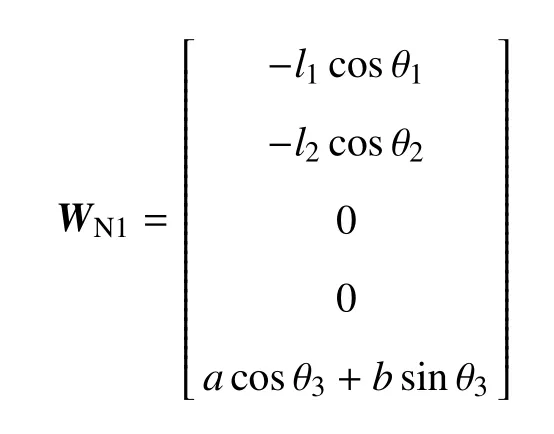
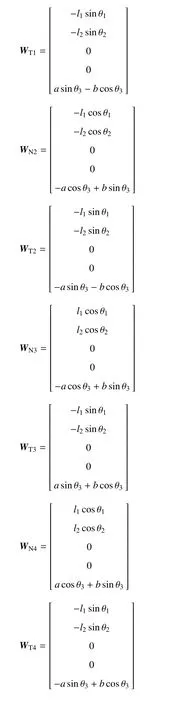
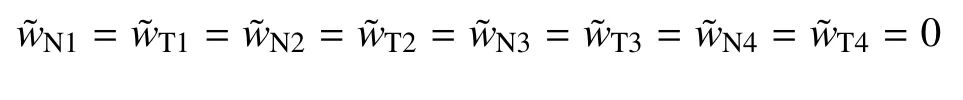
法向约束力和切向摩擦力列阵为

系统全局动力学方程为

图3为曲柄转动两周过程中曲柄角速度、连杆角速度、连杆的角位移和角速度相图以及滑块质心的轨迹图.

图3 Fig.3

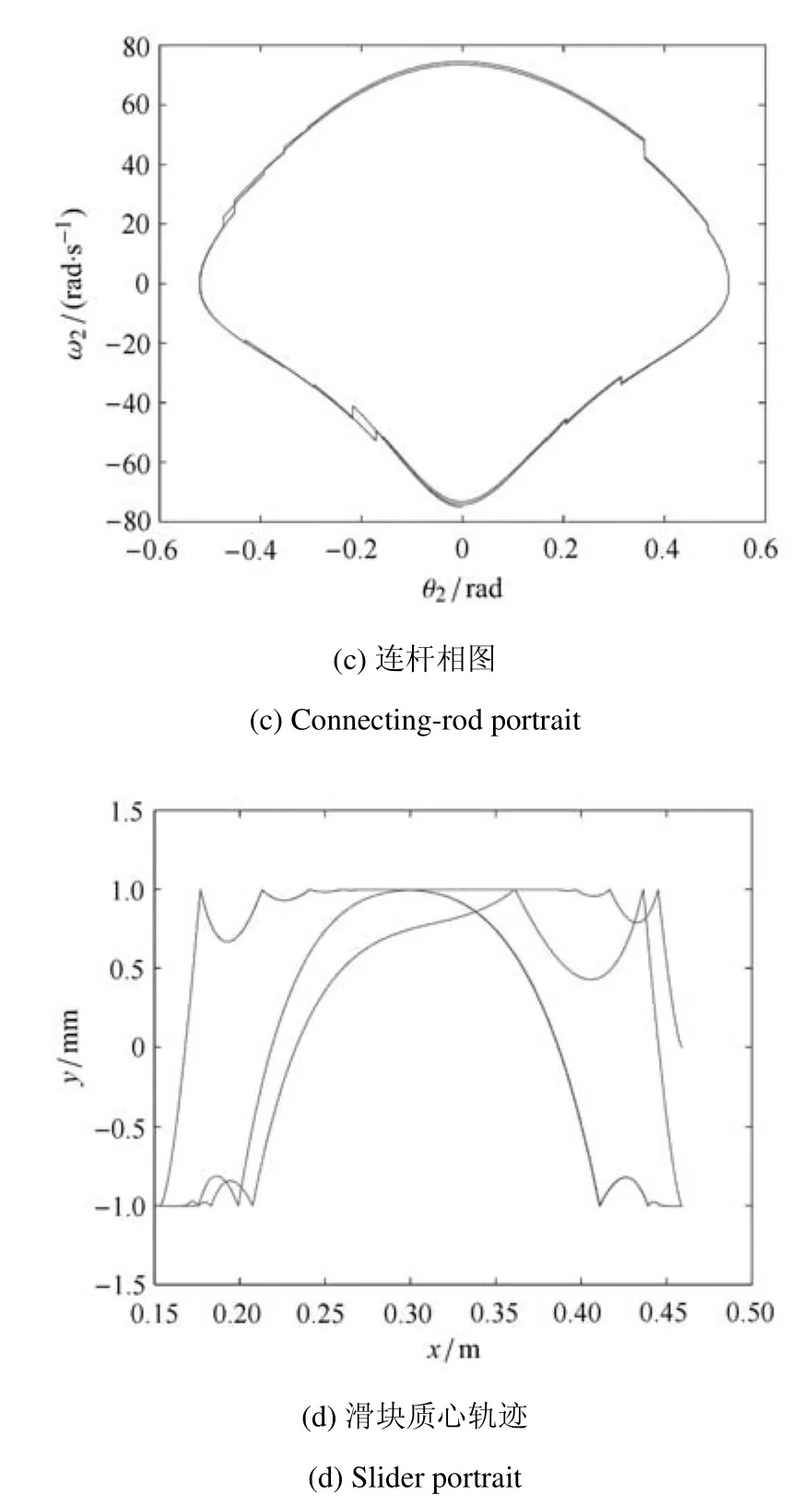
图3 (续)Fig.3(continued)

图4为曲柄转动两周过程中四个角点的运动.从运动曲线中可以观察到滑块的自由运动以及接触碰撞事件的发生.

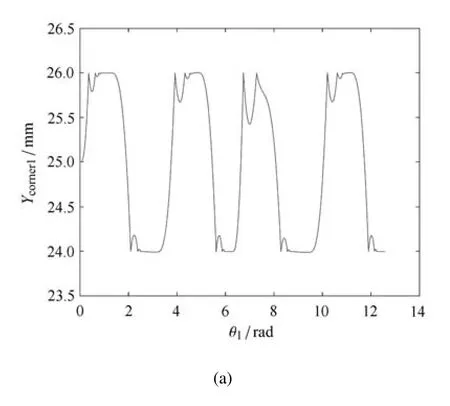
图4 滑块角点的运动Fig.4 Motion of the slider corners

图5显示恢复系数对运动的影响，恢复系数分别取为0.1,0.4,0.7,0.9.

图6显示间隙尺寸对系统响应的影响.间隙尺寸c分别取为0.1，0.2，0.5和1.0mm.

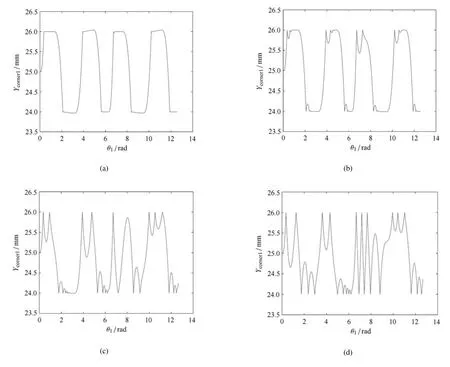
图5 恢复系数对滑块角点1运动的影响Fig.5 In fl uence of the restitution coefficient on the motion of corner 1

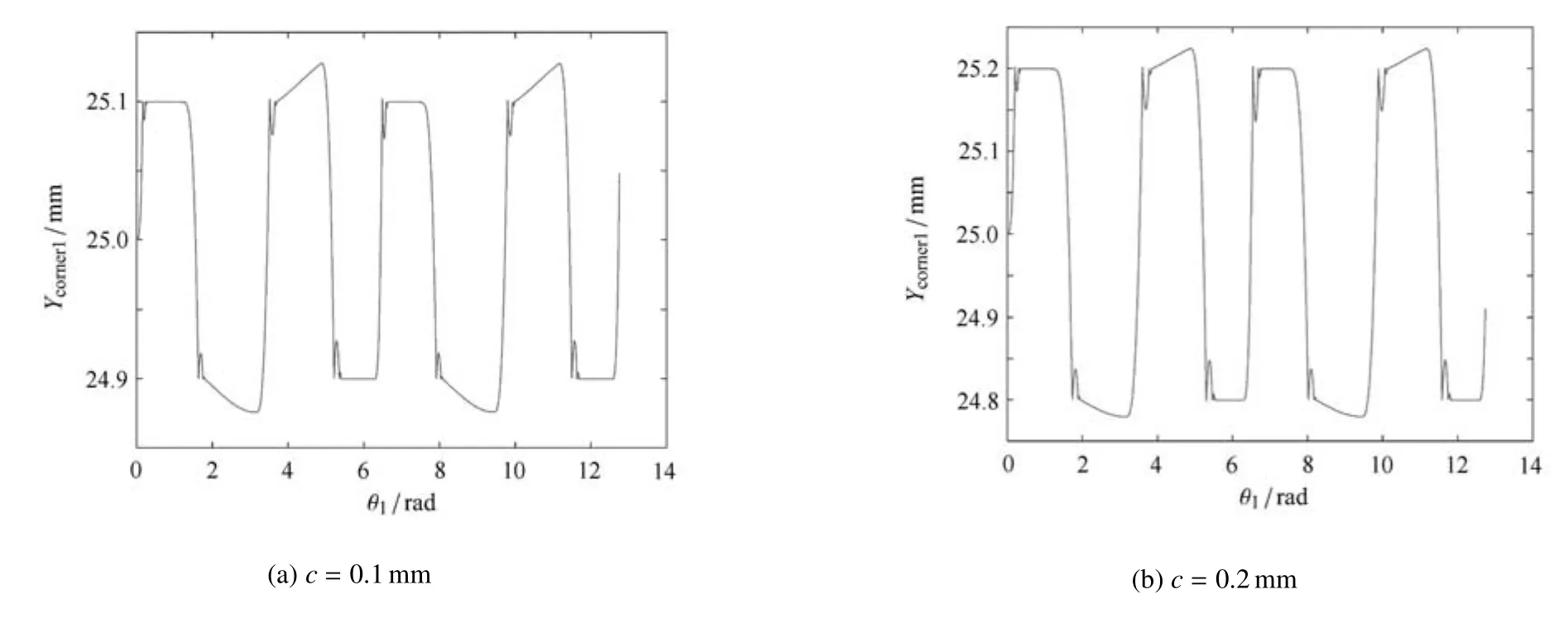
图6 间隙尺寸对滑块角点1运动的影响Fig.6 In fl uence of the clearance size on the motion of corner 1

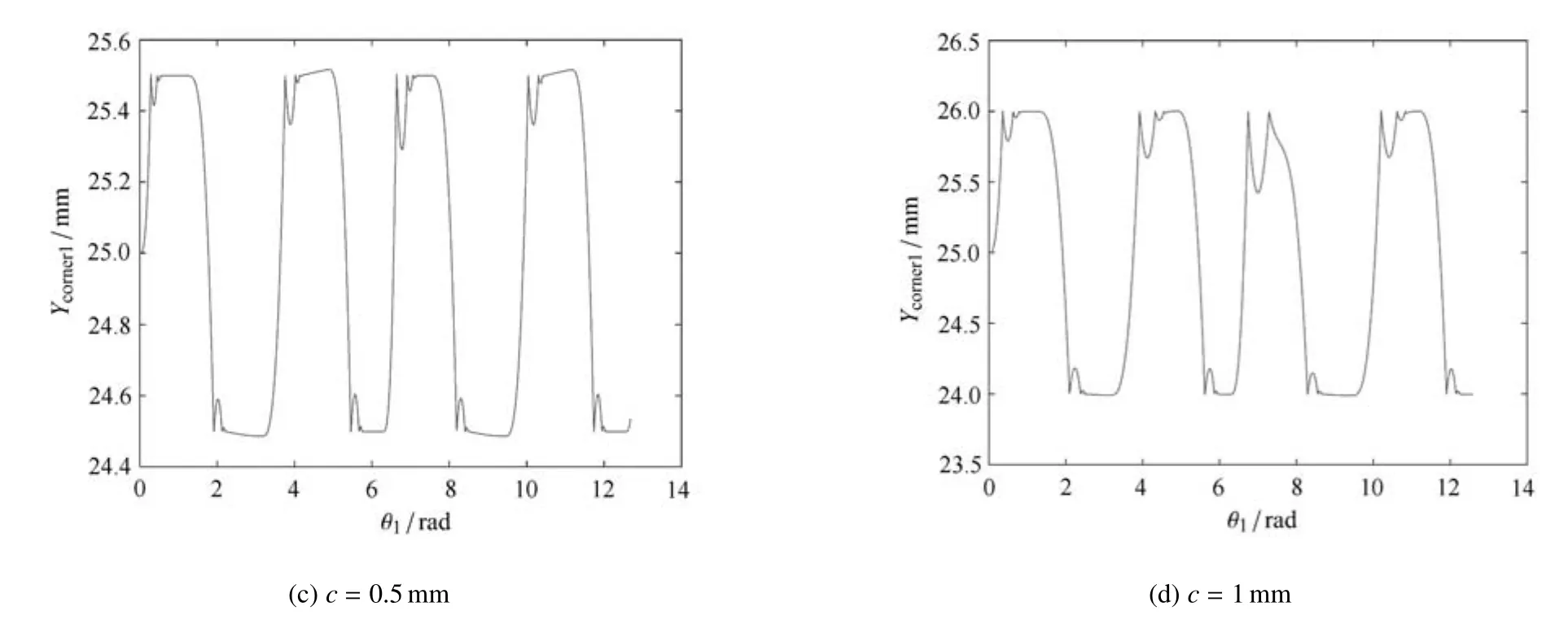
图6 间隙尺寸对滑块角点1运动的影响(续)Fig.6 In fl uence of the clearance size on the motion of corner 1(continued)

4 结论

本文将多体系统的线性互补方法应用于含有光滑等式约束的摩擦、碰撞多体系统.采用牛顿--欧拉方法 (即最大数目坐标法)建立基本系统动力学方程，由于含有等式约束，因此其数学模型是一组微分代数方程.在基本系统上，考虑接触点处的法向和切向互补关系，并通过约束矩阵，将对应的法向、切向拉氏乘子(约束反力)添加加至基本系统微分代数方程中，便构成接触状态下的系统动力学模型.同样地，在基本系统上，考虑碰撞点处的法向和切向互补关系，并通过约束矩阵将对应的法向、切向拉氏乘子(约束反力)加至基本系统微分代数方程中，便构成碰撞时的系统动力学模型.

将单边约束、库仑摩擦定律和牛顿碰撞定律均转化为互补关系来表述，将动力学方程及其所有约束互补关系离散化为速度--冲量形式，采用分块矩阵模型简化推导过程，给出了一种新型线性互补公式.仅考虑单边约束的多体系统动力学问题是常微分方程与线性互补的混合动力学问题，同时含等式约束及不等式约束的多体系统动力学问题是微分代数方程与线性互补的混合动力学问题.数值计算采用时间步进算法，将线性互补解法嵌入至Moreau的时间步进算法之中.数值计算过程中，系统动力学模型将在自由运动、持续接触运动以及碰撞三种运动状态下相互切换，持续接触过程中接触状态也随时间变化，体现了典型的变拓扑结构特征.

最后，通过对含间隙滑移铰曲柄滑块机构的建模与数值分析，验证了本文方法的有效性.

1 Moreau JJ.Unilateral contact and dry friction in fi nite freedom dynamics.In:Moreau JJ,Panagiotopoulos PD.Non-smooth Mechanics and Applications//International Centre for Mechanical Sciences,Courses and Lectures,Vol.302,New York,Springer-Verlag,1988:1-82

2 Panagiotopoulos PD.Inequality Problems in Mechanics and Applications.Boston:Stuttgart,Birkh´auser,1985

3 Brogliato B.Nonsmooth Mechanics:Models,Dynamics and Control,2nd ed.London:Springer-Verlag,1999

4富立.非光滑多体系统动力学线性互补方法.北京：清华大学出版社,2016(Fu Li.LCP Method for Non-smooth Multibody System Dynamics.Beijing:Tsinghua University Press,2016(in Chinese))

5 L¨otstedt P.Mechanical systems of rigid bodies subject to unilateral constraints.Siam Journal on Applied Mathematics,1982,42(2):281-296

6 Bara ff D.Issuesincomputingcontactforcesfornonpenetratingrigid bodies.Algorithmica,1993,10:292-352

7 Pfei ff er F,Glocker C.Multibody Dynamics with Unilateral Contacts//Non-linear Dynamics.Weinheim:John Wiley&Sons,1996

8 Glocker,C,Set-Valued Force Laws-Dynamics of Non-Smooth Systems.Berlin:Springer,2001

9 Stewart DE.Rigid body dynamics with friction and impact.Siam Review,2000,42(1):3-39

10 Anitescu M,Potra FA.Formulationg dynamics multi-rigid-body contact problems with friction as solvable linear complementarity problems.Nonlinear Dynamics,1997,14:231-247

11 Acary V,Brogliato B.Numerical Methods for Nonsmooth Dynamical Systems//Applications in Mechanics and Electronics.Berlin:Springer-Verlag,2008

12 Blumentals A,Brogliato B.The contact problem in Lagrangian sys-tems subject to bilateral and unilateral constraints,with or without sliding Coulomb’s friction:A tutorial.Multibody System Dynamics,2016,1:1-34

13 Zhao Z,Liu CS,Chen B,et al.Asymptotic analysis of Painleve¨s paradox.Multibody System Dynamics，2015,35(3):299-319

14 Glocker Ch.Energetic consistency conditions for standard impacts.In:Part II:Poisson-type inequality impact laws.Multibody System Dynamics,2014,32(1):445-509

15 Dietmayer K.Modelling of unilateral constraints using power-based restriction functions within Lagrangian mechanics.Mathematical&Computer Modelling of Dynamical System,2015,21(3):1-26

16 Glocker C.Simulation of Hard Contacts with Friction.In:An Iterative Projection Method.Recent Trends in Dynamical Systems,Springer,Basel,Switzerland,2013:493-515

17 Schindler T,Rezaei S,Kursawe J,et al.Half-explicit timestepping schemes on velocity level based on time-discontinuous Galerkin methods.Computer Methods in Applied Mechanics and Engineering,2015,290(15):250-276

18 Kikuuwe R,Brogliato B.A new representation of systems with frictional unilateral constraints and its Baumgarte-like relaxation.Multibody System Dynamics,2015,34(7):1-24

19 Pournaras A,Karaoulanis F,Natsiavas S.Dynamics of mechanical systems involving impact and friction using an effi cient contact detection algorithm. http://dx.doi.org/10.1016/j.ijnonlinmec.2016.08.007,2016-8-24

20王晓军,王琪.含摩擦与碰撞平面多刚体系统动力学线性互补算法.力学学报,2015,47(2):814-821(Wang Xiaojun,Wang Qi.A LCP method for the dynamics of planar multibody systems with impact and friction.Chinese Journal of Theoretical and Applied Mechanics,2015,47(2):814-821(in Chinese))

21 Ferrari F，Tasora A，Masarati P,et al.N-body gravitational and contact dynamics for asteroid aggregation.Multibody System Dynamics，2017,39(1):3-20

22张韵，李俊峰.碎石堆小行星的散体动力学建模与仿真方法综述.力学学报,2015,47(1):1-7(Zhangyun,Li Junfeng.A survey of granular dynamics modeling and simulation methods for rubble-pile asteroids.Chinese Journal of Theoretical and Applied Mechanics,2015,47(1):1-7(in Chinese))

23 Zhao Zhen，Liu Caishan，Chen Tao.Docking dynamics between two spacecrafts with APDSes.Multibody System Dynamics，2016,37(3):245-270

24 Yaqubi S,Dardel M.Daniali HM.Modeling and control of crank–slider mechanism with multiple clearance joints.Multibody System Dynamics,2016,36(2):1-25

25 Abdallah MAB,Khemili I,Aifaoui N.Numerical investigation of a fl exible slider–crank mechanism with multijoints with clearance.Multibody System Dynamics,2016,38(2):173-199

26 LimKW,KrabbenhoftK,Jos´eE,etal.Acontactdynamicsapproach to the Granular Element Method.Computer Methods in Applied Mechanics and Engineering,2014,268(1):557-573

27 Leine RI,Schweizer A,Christen M,et al.Simulation of rockfall trajectories with consideration of rock shapein.Multibody System Dynamics,2014,32:241-271

28 Zobova AZ,Nicolas TH,Noot V,et al.Multi-physics modelling of a compliant humanoid robot.Multibody System Dynamics,2017,39(1):95-114

29 Shourijeh MS，Mcphee J.Foot–ground contact modeling within human gait simulations:From Kelvin–Voigt to hyper-volumetric models.Multibody System Dynamics,2015,35(1):393-407

30 Josep JR,Font-Llagunes M,Plaza A,et al.Dynamic considerations of heel-strike impact in human gait.Multibody System Dynamics,2015,35(3):215-232

31洪嘉振.计算多体系统动力学.北京:高等教育出版社,1999(Hong Jiazhen.Computational Dynamics of Multibody Systems.Beijing:Higher Education Press,1999(in Chinese))

32齐朝晖.多体系统动力学.大连:科学出版社,2008(Qi zhaohui.Multi-body System Dynamics.Dalian:Science Press,2008(in Chinese))

33 Shabana AA.Computational Dynamics 3rd ed.West Sussex:John Wiley,2010

34范新秀,王琪.车辆纵向非光滑多体动力学建模与数值算法研究.力学学报,2015,47(2):301-309(Fan Xinxiu,Wang Qi.Research on modeling and simulation of longitudinal vehicle dynamics based on non-smooth dynamics of multibody systems.Journal of Theoretical and Applied Mechanics,2015,47(2):301-309(in Chinese))

CONTACT-IMPACT ANALYSIS IN MULTI-BODY SYSTEMS BASED ON NEWTON-EULER LCP APPROACH1)

Fu Li2)Hu Hongkui Fu Teng
(Science School，North China University of Science and Technology，Tangshan 063210，Hebei，China)

The contact-impact analysis in multibody systems based on the nonsmooth dynamics approach is a hot topic in the research of multibody system dynamics.Newton-Euler approach is adopted to develop dynamics model of contactimpact analysis in non-smooth multi-body systems,and a new LCP formula is presented in this work.Di ff erent from Lagrange methods，Newton-Euler modeling method incorporate equality constraints into dynamic models with noninterpenetration constraints and frictional constraints together.In Newton-Euler modeling method,the basic system is derived by removing the non-interpenetration constraints and frictional constraints from the original multi-body system.Newton-Euler eqution of basic system is established by using the maximum coordinates method.Because the coordinates of the basic system are not independent of each other,equality constraints are involved in modeling,the basic system dynamic equations is a set of DAE(di ff erential algebra equation).With the aid of constraint Jacobian matrix,Lagrangian multipliers corresponding to the non-interpenetration constraint forces and Coulomb friction forces are added to the basic system DAE to obtain the dynamic equations of global motion of the multi-body system with characteristics of variable topologicalstructure.ThecompletedynamicmodeliscomposedofbasicsystemDAE,equalityandinequalityconstraints.In order to simplify the derivation process of LCP,a decomposed matrix form is built.The LCP-based Time-stepping method is adopted for numerical simulation.Time-stepping algorithm is a popular non-smooth numerical algorithm,Its prominent feature is that it can avoid the tedious event-detection process in numerical integration.In the process of numerical integration,the contact-detachment state of the system can be determined by solving the LCP.Our method is carried out in slider-crank mechanism with a translational clearance joint,the simulation results indicate that this method is e ff ective.

non-smooth,multi-body system,friction,collision,LCP

O313.7

A

10.6052/0459-1879-17-023

2017–01–18收稿，2017–06–07 录用,2017–06–20 网络版发表.

1)河北省自然科学基金资助项目(A2013209221).

2)富立，教授，主要研究方向：多体系统动力学及非线性动力学.E-mail：13231554976@163.com

富立,胡鸿奎,富腾.多体系统接触碰撞问题的牛顿--欧拉线性互补方法.力学学报,2017,49(5):1115-1125

Fu Li,Hu Hongkui,Fu Teng.Contact-impact analysis in multi-body systems based on Newton-Euler LCP approach.Chinese Journal of Theoretical and Applied Mechanics,2017,49(5):1115-1125