不同状态方程对固体介质中斜激波反射的影响1)

黄 萧 于 鑫

(北京应用物理与计算数学研究所，北京100094)

不同状态方程对固体介质中斜激波反射的影响1)

黄 萧 于 鑫2)

(北京应用物理与计算数学研究所，北京100094)

相比气体，固体介质在高压下的状态方程更为复杂，形式也多种多样．现有关于固体介质中激波反射的理论研究，一般直接采用某种状态方程，缺乏对采用不同状态方程得到的结果的对比．本项工作采用激波极曲线的理论分析方法，选择4种不同组合形式的状态方程(一次冲击激波采用线性的冲击波速度与粒子速度关系式，二次冲击激波采用Gr¨uneisen状态方程；一次冲击和二次冲击激波均采用冲击波速度与粒子速度关系式；一次冲击激波采用线性冲击波速度与粒子速度关系式,二次冲击激波采用刚性气体状态方程；以及一次冲击激波和二次冲击激波均采用刚性气体状态方程)，研究固体介质中的斜激波反射，比较了采用不同组合形式的状态方程对反射激波波后压力的影响．利用量纲分析方法讨论了简化状态方程达到较高精度的条件．此外，用ANSYS/LS-DYNA软件，对激波极曲线理论给出的结果进行了验证．本项工作可为固体介质中激波反射问题状态方程的选取提供一定的指导．

斜激波反射，激波极曲线，状态方程，固体介质

引言

工程研究中经常涉及固体介质里的激波反射问题，如高能炸药的爆轰波与固体结构的相互作用、弹丸侵彻固体靶片、两物体高速碰撞产生射流等[16]．爆轰波在固体介质中诱导产生的斜激波，或者物体高速斜碰撞产生的斜激波，在遇到固壁、交界面时会发生反射,产生较高的压力．急剧升高的压力可能在固体介质中引发特殊的力学现象[78]，因此开展相关研究对国防应用及民用经济都具有重要的意义．

气体里的激波反射现象很早就受到关注[9].马赫最早在实验中发现并记录了激波反射现象，他记录了两种不同的激波反射结构，一种是正规反射，另一种是马赫反射．之后冯·诺依曼针对正规反射和马赫反射分别提出了“两激波理论”和“三激波理论”，求解得到反射点附近各区域的流动参数．由于激波反射求解中边界条件的约束是转角和压强，在实际应用中更为有效的是压力–转角极曲线[1014]．例如反射激波极曲线与纵轴的交点是正规反射的解，而马赫杆极曲线与反射激波极曲线的交点即为马赫反射的解．通常根据激波的运动状态又可以分为定常的反射结构和非定常的反射结构．气体中超音速来流绕楔角的流动会产生驻定的激波反射结构，而运动激波沿楔面的运动会产生准定常的反射结构，准定常的反射形式比定常的更为丰富，例如有可能产生双马赫反射[15]．

相比气体，固体介质中斜激波反射的系统研究工作在公开发表的文献中鲜有出现．原因之一是固体介质在高压下的状态方程较为复杂，可采用的状态方程形式也多种多样,例如冲击波速度与波后粒子速度关系、Gr¨uneisen状态方程、刚性气体状态方程等[1619]．近年关于固体介质中激波反射的研究，一般直接采用某种状态方程，例如陈大伟等[20]采用刚性气体状态方程研究了凝聚介质里的斜激波反射问题，Brown和Ravichandran[21]采用Gr¨uneisen状态方程研究了固体介质界面间的激波折射．可以看到这类研究缺乏对不同形式状态方程得到的结果的对比，若能给出采用不同状态方程得到结果之间的差异，对以后的理论或数值模拟具有重要的意义，例如能对采用某种状态方程得到结果的精度有定量的认识．因此本工作基于激波极曲线的理论分析方法，比较在不同状态方程下固体介质中的斜激波反射，探讨采用不同状态方程对反射激波波后压力精度的影响．

1 理论模型

1.1 状态方程

图1描述了一个典型的马赫反射结构.入射激波(OI)和马赫杆(OT)是一次冲击激波，而反射激波(OR)是二次冲击激波.采用不同的状态方程,得到的一次冲击激波关系式和二次冲击激波关系式会不同．对于一次冲击，大量的实验研究表明，许多固体材料的冲击波速度与粒子速度呈现线性关系[2223]

图1 马赫反射结构示意图Fig.1 Schematic diagram of a Mach re fl ection

其中,常压下的声速c0和λ均为材料参数．对于二次冲击，并没有直接的实验性的经验关系式．本文研究4种不同组合形式状态方程下的斜激波反射问题.一次冲击激波采用线性的冲击波速度与粒子速度关系式,二次冲击激波采用Gr¨uneisen状态方程，用1Du2Gr¨uneisen表示;一次冲击激波采用线性冲击波速度与粒子速度关系式,二次冲击激波采用二次的冲击波速度与粒子速度关系式，用1Du2Du表示;一次冲击激波采用线性冲击波速度与粒子速度关系式、二次冲击激波采用刚性气体状态方程，用1Du2Gama表示;一次冲击激波和二次冲击激波均采用刚性气体状态方程,用 1Gama2Gama表示．由于固体介质参数的测定利用Gr¨uneisen状态方程，一次冲击利用冲击波速度与粒子速度关系式．因此本文假设理论上1Du2Gr¨uneisen状态方程得到的结果与实验结果是一致的，在后续的理论分析中，以1Du2Gr¨uneisen得到的结果作为参考值，比较另外3种状态方程与其差异．

1.2 激波极曲线关系式

1.2.1 采用1Du2Gr¨uneisen状态方程

对于一次冲击采用线性的冲击波速度与粒子速度关系式，激波极曲线关系式为

其中 p0和 p1分别表示入射激波波前和波后的压力，对于固体介质，通常令p0=0．ρ0和q0分别表示入射激波波前的密度和来流速度(参考系固定在激波上)，D1和u1分别表示入射激波速度和波后的粒子速度，θ1为入射激波波前、波后速度的转角．对于二次冲击激波，Brown和Ravichandran[21]给出采用Gr¨uneisen状态方程时的压力与比容(p-v)关系如下

其中v0为初始状态下的比容，v2和p2分别表示反射激波波后的比容和压力，Γ为材料参数，为简便起见，取 Γ/v= Γ0/v0及 Γ0=2λ−2/3[24]．反射激波波前、波后速度的转角θ2有如下关系式

其中v1和q1分别表示反射激波波前的比容和来流速度(参考系固结在激波上)．式(3)和式(4)构成反射激波采用Gr¨uneisen状态方程时的激波极曲线关系式．

1.2.2 采用1Du2Du状态方程

一次冲击的激波极曲线关系同式(2)，二次冲击的冲击波速度和粒子速度的关系可设为

其中 a1,b1和 c1为待定参数，D2nr和 u2nr分别表示相对于u1n的反射激波速度和波后粒子速度，即D2nr=D2n−u1n和u2nr=u2n−u1n，其中u1n为入射激波波后粒子速度u1在垂直于反射激波方向上的分量．相对一次冲击时的冲击波速度与粒子速度关系式(1)，式(5)的参数较难通过实验进行标定，Neal[25]和经福谦[26]给出了一种把压力--比容关系转换为冲击波速度--粒子速度关系的方法，基于此，待定参数a1,b1和c1可表示为

若采用Gr¨uneisen状态方程来表示二次冲击时的p-v关系，结合式(3)和(6)可以得到a1,b1和c1的具体表达式，从而得到反射激波采用冲击波速度与粒子速度关系式时的激波极曲线关系式

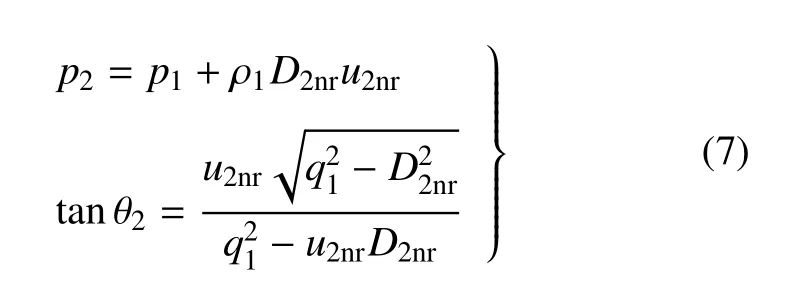
实际上，此时反射激波采用冲击波速度与粒子速度关系式等效于采用Gr¨uneisen状态方程的二阶近似．

1.2.3 采用1Du2Gama状态方程

一次冲击的激波极曲线关系同式(2)，二次冲击采用刚性状态方程时的激波极曲线关系可表示为

其中 γ为绝热指数．为方便不同状态方程间的比较，绝热指数γ取为等熵的常数近似γ=2λ−1+

1.2.4 采用1Gama2Gama状态方程

此时所有激波关系式均采用刚性气体状态方程，对于一次冲击的入射激波和马赫杆，有如下激波极曲线关系

对于二次冲击的反射激波，激波极曲线关系同式(8)．

2 理论分析结果和讨论

2.1 不同形式状态方程对激波极曲线的影响

以金属铍(Be)为例，给定材料参数：常压下的声速 c0=0.799cm/µs、初始密度 ρ0=1.85g/cm3以及系数λ=1.13，加载条件给定入射激波强度，即入射激波波后压力p1=100GPa．图2给出了不同入射激波倾角α0下的激波极曲线图，当α0=35°时，从图2(a)可以看出，此时发生正规反射，采用1Du2Du状态方程的解和1Du2Gr¨uneisen最为接近，而1Du2Gama偏离1Du2Gr¨uneisen较多．

当入射激波倾角α0=45°时，激波极曲线图2(b)显示了4种不同状态方程下马赫杆极曲线和反射激波极曲线的交点，可以看出此时发生的是非正规反射，而且采用不同状态方程得到的结果差异明显.这种差异不仅反映在反射激波波后压力上，也表现在反射模式上．当采用1Du2Gama和1Gama2Gama状态方程时，交点在反射激波极曲线顶点的左侧，发生的是马赫反射(MR)，而采用1Du2Gr¨uneisen和1Du2Du状态方程时，交点在反射激波极曲线顶点的右侧，此时发生的是冯·诺依曼反射(vNR)[11,2931]．

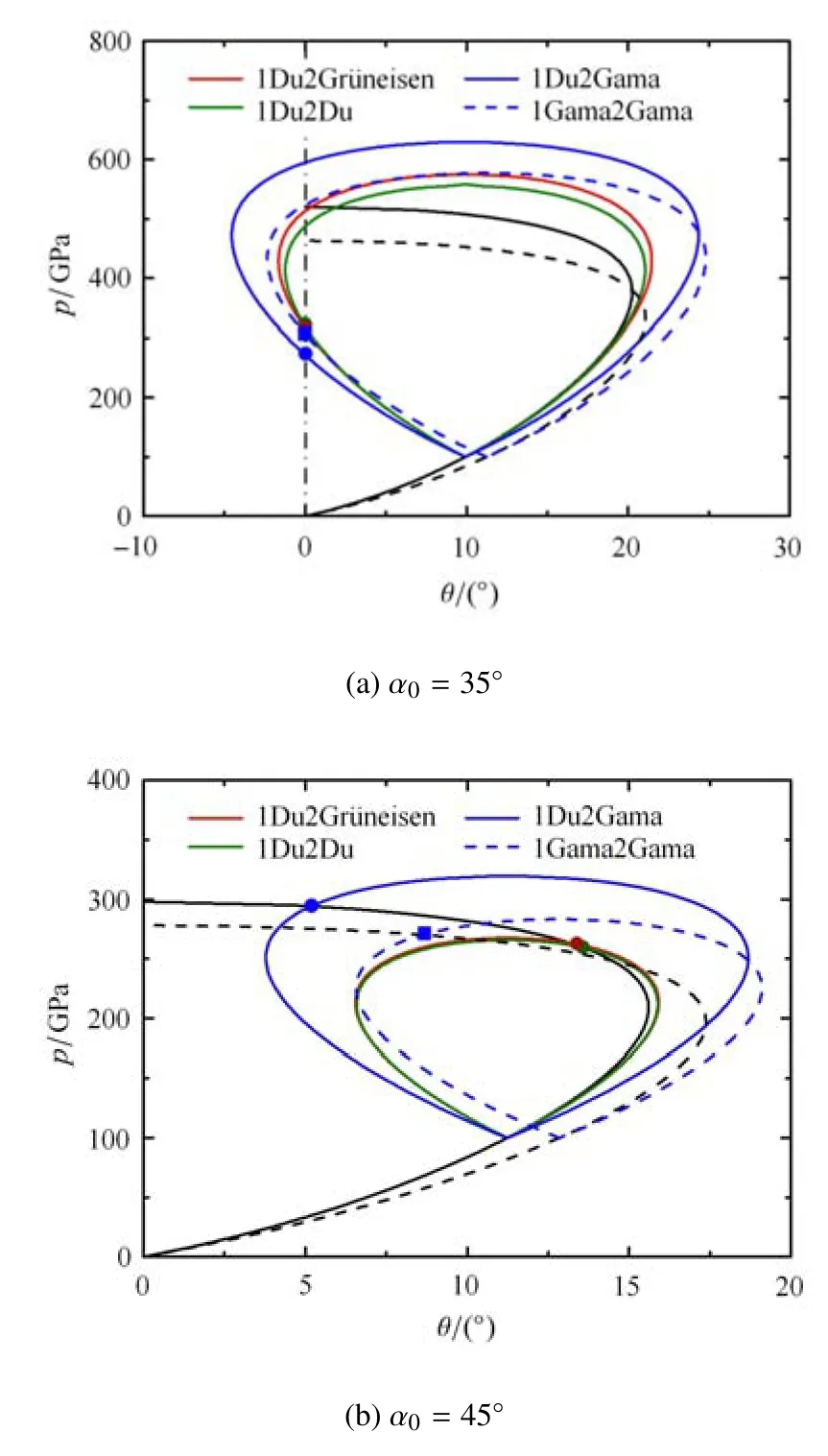
图2 不同入射激波倾角下的激波极曲线Fig.2 Shock polar under di ff erent incident angles

2.2 不同形式状态方程对反射激波波后压力的影响

改变入射激波倾角 α0，可以得到在给定激波强度条件下，反射波波后压力 p2随 α0的变化．图3描绘了不同状态方程对反射激波波后压力的影响．从图中可以看出，采用1Du2Du状态方程的解和1Du2Gr¨uneisen最为接近，而1Du2Gama的解和1Du2Gr¨uneisen偏离最远．而且，总体上正规反射阶段4种状态方程得出的结果差异较小，非正规反射阶段得出的结果差异较为明显．

图3 不同状态方程对反射激波波后压力的影响Fig.3 E ff ect of di ff erent equations of state on the pressure behind the re fl ected shock

此外，图3表明随着α0增大到某一角度时，p2的值会发生突变，此时对应的角度即为正规反射过渡到非正规反射的临界角．当入射激波强度较大(如p1=100GPa)时，采用不同状态方程得出的临界角在37°到42°之间，而强度较小(如 p1=15GPa)的入射激波给出的临界角在47°到57°之间，此时采用不同状态方程得到的结果之间差距更大．

2.3 不同形式状态方程对反射类型的影响

根据反射激波脱体的判据，由激波极曲线理论可以得到不同入射激波强度下从正规反射过渡到非正规反射的临界角，由此可将激波反射类型划分为两个区域：正规反射区和非正规反射区，如图4所示．横轴为代表入射激波强度的入射激波波后压力，纵轴为入射激波与来流的角度．从图中可以看出，入射激波强度越小，从正规反射过渡到非正规反射的临界角越大．此外，图中表明采用 4种不同状态方程得到的区域分界线差异较为明显，由1Du2Du和1Du2Gr¨uneisen得到的结果基本一致，由1Gama2Gama得到的结果与1Du2Gr¨uneisen有所差异，1Du2Gama得到的结果与1Du2Gr¨uneisen差异最大．由此可见，采用不同状态方程对反射激波波后压力以及反射类型的判定都有较大的影响，在实际应用中需要加以注意．

图4 激波反射区域类型的划分Fig.4 Domains of di ff erent types of shock wave re fl ection

2.4 量纲分析

前面的小节给出了特定材料参数下的结果，接下来通过量纲分析研究更一般的结果，并基于此给出简化形式的刚性气体状态方程的适用条件．对于本文研究的问题，反射激波波后压力是以下独立参数的函数

即p2只与初始密度ρ0、声速c0、一次冲击D−u关系式的系数λ、代表入射激波强度的p1以及入射激波的倾角α0有关．这5个参数只存在两个具有独立量纲的参数，不失一般性，选为ρ0和c0，其他参数的量纲可以由这两个基本参数的量纲导出，利用量纲分析中的π定理，式(10)可以重新写为如下的无量纲函数形式

即无量纲化的反射激波波后压力只与无量纲化的入射激波波后压力、λ以及α0相关，无量纲化后可将原本需要讨论的5个参数降为3个，很大程度上简化了问题．

图5 正规反射阶段不同状态方程解的误差Fig.5 Solution error of regular re fl ection under di ff erent equations of state

当入射激波的倾角 α0较小时，系统产生正规反射，在正规反射阶段反射激波波后压力随倾角增大变化不大.给定 α0=20°，讨论不同的 λ值下，随的变化，并比较4种不同形式状态方程的影响，此时结果可近似表示正规反射阶段不同状态方程对无量纲化的反射激波波后压力的影响．以1Du2Gr¨uneisen得到的值为标准，比较另外3种状态方程得到的值相对其的误差η，η随的变化趋势如图5所示．从图中可以看出，对于1Du2Du，大多数情况下得到的结果都很精确，因为其是1Du2Gr¨uneisen解的二阶近似.对于1Du2Gama，在λ为1.5～1.8时得到的结果与1Du2Gr¨uneisen符合得较好，λ为其他值时精度较差.而对于1Gama2Gama，在λ为1.2～1.3时得到的结果与1Du2Gr¨uneisen符合得较好;λ为其他值时只有

图5 正规反射阶段不同状态方程解的误差(续)Fig.5 Solution error of regular re fl ection under di ff erent equations of state(continued)

图6 非正规反射阶段不同状态方程解的误差Fig.6 Solution error of irregular re fl ection under di ff erent equations of state

当入射激波倾角较大时，系统有可能出现非正规反射，在正规反射和非正规反射过渡的阶段，不同状态方程对结果的影响较为剧烈．图6(a)和图6(b)分别描绘了在入射激波倾角α0=35°及α0=40°条件下的误差随的变化趋势，此时给定λ=1.2．从图中可以看出，随着无量纲化入射激波强度增大，不同状态方程得到解的误差都会出现突然增大，而在一定区间后又会突然减小的现象．此区间对应着系统的解从正规反射到非正规反射的过渡区，该过渡区也可以从图4加以解释，即为以α0等于定值的直线交于不同状态方程得到的区域分界线的区间段，从图中可以看出1Du2Gama的过渡区最大．在过渡区内另外3种状态方程的相对误差都较大(η接近50%)．而当的值小于此区间时，系统的解为正规反射，从图中可以看出1Du2Du得到的结果很精确，而1Du2Gama的结果误差最大，约为10%．当的值大于此区间时，系统的解为非正规反射，从图中可以看出1Du2Du得到的结果很精确，而1Gama2Gama的结果误差最大，约为10%．

综上所述，对于大多数固体(λ=1.2左右)，无论是求解正规反射还是非正规反射问题，采用简化形式的刚性状态方程(1Gama2Gama或1Du2Gama)均会带来一定的误差．采用1Gama2Gama得到的解误差在正规反射问题时比1Du2Gama小，误差在5%以内；而采用1Du2Gama得到的解误差在非正规反射问题时比1Gama2Gama小，误差在5%以内．在正规反射到非正规反射的转变阶段，1Du2Gama得到的解误差在过渡区最大，建议相关理论研究工作慎重采用．

3 数值模拟

为验证激波极曲线理论得出的结果，利用有限元程序ANSYS/LS-DYNA对不同入射激波倾角下的激波反射进行模拟．由于固体介质中的斜激波反射一般非定常，因此建立运动激波过楔面发生反射的数值模型．计算模型如图7所示，左侧给定入射激波波后压力的边界条件，上边、下边和斜边施加滑移固壁边界条件，模型采用固定的欧拉网格．固体介质采用Gr¨uneisen状态方程，材料参数同3.1节．图7中α为入射激波和楔面的夹角，由于非正规反射中来流方向平行于三波点轨迹线，而非平行于固壁，因此当运动激波发生非正规反射时，激波极曲线理论需要相应地考虑三波点轨迹角的影响，此时有α=α0+δ．

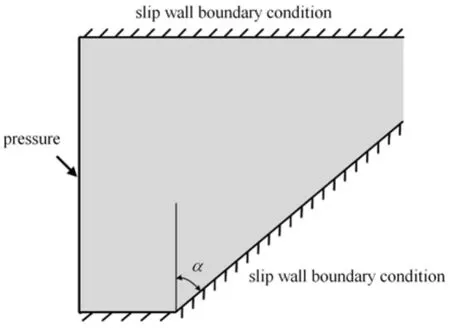
图7 激波反射数值模拟的有限元模型Fig.7 Finite element model for numerical simulations of shock wave re fl ection

随着入射激波和楔面夹角 α的增大，数值模拟得到的斜激波反射波后状态及反射模式将发生改变，图 8(a)～ 图 8(c)描绘了 α =35°,α =45°和α=66°时数值模拟给出的斜激波反射模式以及相应的激波极曲线理论解．

图8 不同入射激波倾角下的密度等值线图及相应的激波极曲线Fig.8 Density contours and the corresponding shock polar under di ff erent incident angles

当α=35°时，理论分析中反射激波极曲线和纵轴有交点，说明此时发生正规反射，数值模拟的图8(a)给出了由入射激波和反射激波组成的二波结构，即正规反射结构．当α=45°时，理论分析中马赫杆极曲线和反射激波极曲线的交点位于反射激波极曲线顶点的左侧，说明此时发生马赫反射.从图8(b)可以清晰地看到由入射激波、弧形的反射激波和马赫杆组成的三波结构，因此结果为马赫反射．继续增大α到66°，激波极曲线理论表明状态方程采用1Du2Gr¨uneisen和1Du2Du得到的交点位于反射激波极曲线顶点的右侧，即 vNR 反射，而采用1Du2Gama和1Gama2Gama状态方程得到的交点位于反射激波极曲线顶点的左侧，因此仍然为马赫反射．从图8(c)数值模拟的结果可以看出，此时发生的是vNR反射，相比马赫反射，vNR反射结构中马赫杆和入射激波之间光滑连接，而且三波点附近的反射波是连续的压缩波．数值模拟的结果表明与采用1Du2Gr¨uneisen和1Du2Du状态方程得到的结果更为一致．

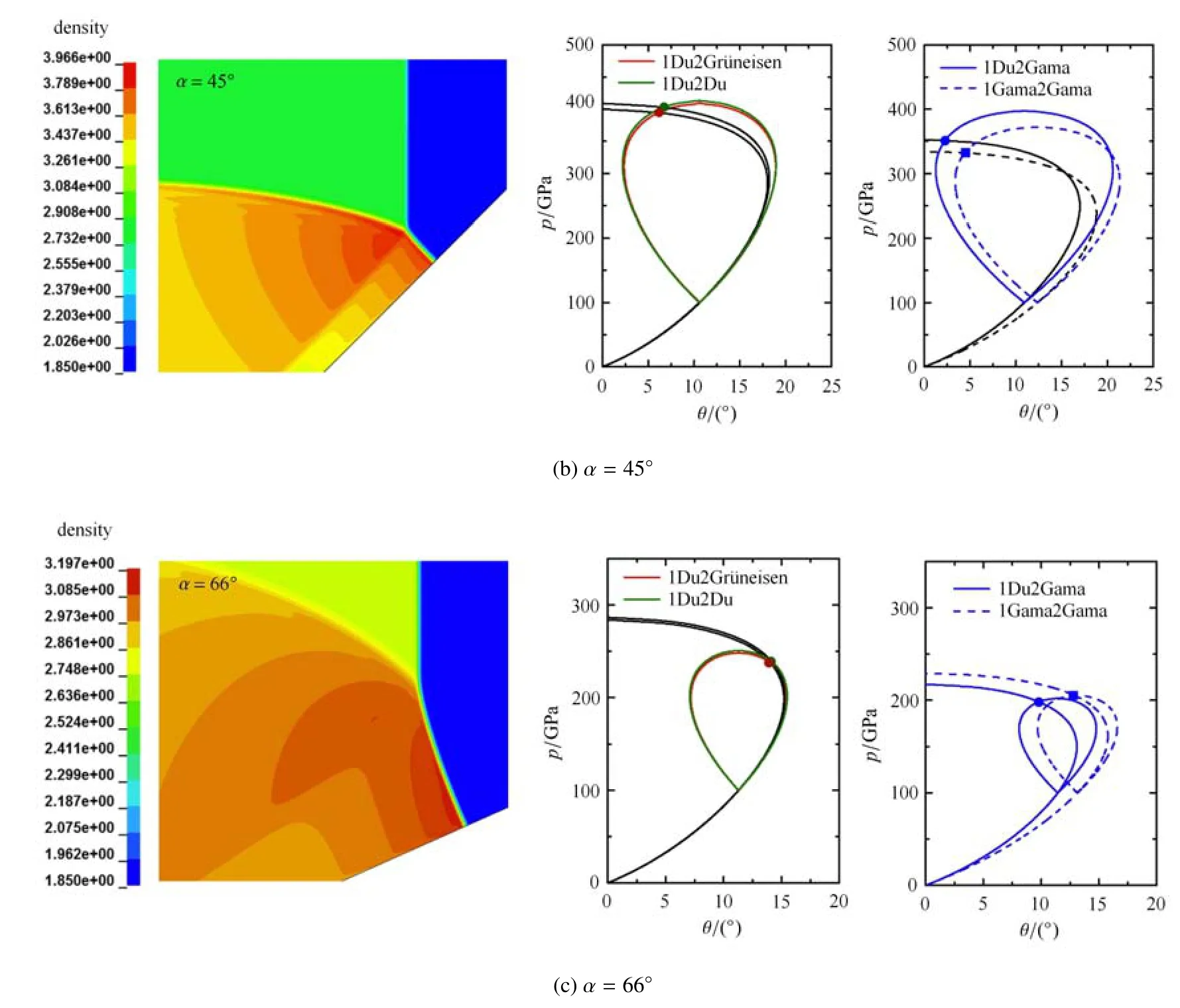
图8 不同入射激波倾角下的密度等值线图及相应的激波极曲线(续)Fig.8 Density contours and the corresponding shock polar under di ff erent incident angles(continued)

4 结论

本文利用激波极曲线的理论分析方法，研究不同形式状态方程对固体介质中斜激波反射的影响．结果表明：

(1)不同的状态方程对反射激波波后压力以及对反射类型的判别都有较大的影响，在实际应用中需要加以注意．

(2)采用冲击波速度和波后粒子速度关系或Gr¨uneisen状态方程得到的结果比采用刚性气体状态方程更为精确．

(3)通过量纲分析讨论了采用刚性气体状态方程能达到较高精度的条件：对于大多数固体(λ=1.2左右)，在求解正规反射问题时，一次和二次激波均采用刚性气体状态方程得到的解误差比一次采用线性冲击波速度与粒子速度关系式、二次采用刚性气体状态方程小，误差在5%以内；而在求解非正规反射问题时，一次激波采用线性冲击波速度与粒子速度关系式、二次激波采用刚性气体状态方程得到的解误差比一次和二次激波均采用刚性气体状态方程小，误差在5%以内．

1 Loomis E,Swift D.Oblique shock waves incident on an interface between two materials for general equations of state.Journal of Applied Physics,2008,103(2):023518

2马天宝,任会兰,李健等.爆炸与冲击问题的大规模高精度计算.力学学报,2016,48(3):599-608(Ma Tianbao,Ren Huilan,Li Jian,et al.Large scale high precision computation for explosion and impactproblems.ChineseJournalofTheoreticalandAppliedMechanics,2016,48(3):599-608(in Chinese))

3王成,王万军,宁建国.聚能装药对混凝土靶板的侵彻研究.力学学报,2015,47(4):672-686(Wang Cheng,Wang Wanjun,Ning Jianguo.Investigation on shaped charge penetration into concretetargets.Chinese Journal of Theoretical and Applied Mechanics,2015,47(4):672-686(in Chinese))

4于明,孙宇涛,刘全.爆轰波在炸药--金属界面上的折射分析.物理学报,2015,64(11):282-291(Yu Ming,Sun Yutao,Liu Quan.Analysis on refraction of detonation wave at the explosive-metal interface.Acta Physica Sinica,2015,47(4):672-686(in Chinese))

5于明,刘全.凝聚炸药爆轰波在高声速材料界面上的折射现象分析.物理学报,2016,65(2):235-244(Yu Ming,Liu Quan.Refraction of detonation wave at interface between condensed explosives and high sound-speed material.Acta Physica Sinica,2016,65(2):235-244(in Chinese))

6魏晨慧,朱万成,白羽等.不同节理角度和地应力条件下岩石双孔爆破的数值模拟.力学学报,2016,48(4):926-935(Wei Chenhui,Zhu Wancheng,Bai Yu,et al.Numerical simulation on two-hole blasting of rock under di ff erent joint angles and in-situ stress conditions.Chinese Journal of Theoretical and Applied Mechanics,2016,48(4):926-935(in Chinese))

7 Singh M,Suneja HR,Bola MS,et al.Dynamic tensile deformation and fracture of metal cylinders at high strain rates.International Journal of Impact Engineering,2002,27(9):939-954

8张崇玉,胡海波,李庆忠等.爆轰波对碰驱动下平面铅飞层对碰区动载行为实验研究.高压物理学报,2009,23(4):283-287(Zhang Chongyu,Hu Haibo,Li Qingzhong,et al.Experimental study on dynamic behavior of lead plate driven by two head-on colliding detonation waves.Chinese Journal of High Pressure Physics,2009,23(4):283-287(in Chinese))

9 Hornung H.Regular and Mach re fl ection of shock waves.Annual Review of Fluid Mechanics,1986,18:33-58

10 Henderson LF,Colella P,Puckett EG.On the refraction of shock waves at a slow–fast gas interface.Journal of Fluid Mechanics,1991,224:1-27

11 Ben-Dor G.Shock Wave Re fl ection Phenomena. New York:Springer,2007

12 Gvozdeva L,Gavrenkov S,Nesterov A.A study of slipstreams in triple shock wave con fi gurations.Shock Waves,2015,25(3):283-291

13 Matheis J,Hickel S.On the transition between regular and irregular shock patterns of shock-wave/boundary-layer interactions.Journal of Fluid Mechanics,2015,776:200-234

14 Kobayashi S,Adachi T.Shock-tube experiments on the stability of regular re fl ection in the dual-solution domain.Shock Waves,2016,26(3):263-267

15 Li H,Ben-Dor G.Reconsideration of pseudo-steady shock wave re fl ections and the transition criteria between them.Shock Waves,1995,5(1):59-73

16 Meniko ffR,Plohr BJ.The Riemann problem for fl uid fl ow of real materials.Reviews of Modern Physics,1989,61(1):75-130

17王继海.二维非定常流和激波.北京:科学出版社,1994(Wang Jihai.Two-Dimensional Unsteady Flow and Shock Waves.Beijing:Science Press,1994(in Chinese))

18 Davison L.Fundamentals of Shock Wave Propagation in Solids.Berlin:Springer,2008

19 McCoy CA,Gregor MC,Polsin DN,et al.Shock-wave equationof-state measurements in fused silica up to 1600GPa.Journal of Applied Physics,2016,119(21):215901

20陈大伟,秦承森,王裴等.凝聚介质中斜激波的反射.计算物理,2011,28(6):791-796(Chen Dawei,Qin Chengsen,Wang Pei,et al.Oblique shock wave re fl ection in condensed matter.Chinese Journal of Computational Physics,2011,28(6):791-796(in Chinese))

21 Brown JL,Ravichandran G.Analysis of oblique shock waves in solids using shock polars.Shock Waves,2014,24(4):403-413

22 Ruo ff AL.Linear shock-velocity-particle-velocity relationship.Journal of Applied Physics,1967,38(13):4976-4980

23 Neal T.Mach waves and re fl ected rarefactions in aluminum.Journal of Applied Physics,1975,46(6):2521-2527

24谭华.实验冲击波物理导引.北京:国防工业出版社,2007(Tan Hua.Introduction to Experimental Shock-Wave Physics.Beijing:National Defense Industry Press,2007(in Chinese))

25 Neal T.Second Hugoniot relationship for solids.Journal of Physics and Chemistry of Solids,1977,38(3):225-231

26经福谦.冲击波速度–粒子速度关系式的一个简单推导及其直线表达式适用范围的讨论.爆炸与冲击,1982(3):17-24(Jing Fuqian. A simpli fi ed derivation of the shock-velocity-particlevelocity relationship and discussion on the applicable range of its linearized expression.Explosion and Shock Waves,1982(3):17-24(in Chinese))

27李维新.凝聚介质的简化状态方程.爆炸与冲击,1983(2):30-38(Li Weixin.A simpli fi ed equation of state in condensed medium.Explosion and Shock Waves,1983(2):30-38(in Chinese))

28李维新.一维不定常流与冲击波.北京:国防工业出版社,2003(Li Weixin.One-dimensional Nonsteady Flow and Shock Waves.Beijing:National Defence Industry Press,2003(in Chinese))

29 Ben-Dor G,Takayama K.The phenomena of shock wave re fl ection—A review of unsolved problems and future research needs.Shock Waves,1992,2(4):211-223

30 Kobayashi S,Adachi T,Suzuki T.Non-self-similar behavior of the von Neumann re fl ection.Physics of Fluids,2000,12(7):1869-1877

31 Wu F,Dai H,Kong D.Mechanism for the transition from a regular re fl ection to a mach re fl ection or a von neumann re fl ection.Acta Mathematica Scientia,2016,36(3):931-944

EFFECTS OF DIFFERENT EQUATIONS OF STATE ON THE OBLIQUE SHOCK WAVE REFLECTION IN SOLIDS1)

Huang Xiao Yu Xin2)
(Institute of Applied Physics and Computational Mathematics，Beijing 100094，China)

The equations of state of solids under high pressure are more complicated than that of gases in a variety of forms.While the existing investigations on the oblique shock wave re fl ection usually take one of the equations of state,lacking of the comparisons among them.Therefore,this paper aims at the oblique shock wave re fl ection in solids through shock polar methodology under four di ff erent forms of equations of state(principal shock taking with linear shock–particle velocity relationship and second shock taking with Gr¨uneisen equation of state,principal and second shock both taking with shock–particle velocity relationship,principal shock taking with linear shock–particle velocity relationship and second shock taking with sti ff ened gas equation of state,and principal and second shock both taking with sti ff ened gas equation of state).The e ff ects of di ff erent equations of state on the pressure behind the re fl ected shock wave are discussed.By conducting the dimensional analysis,we provide an applicable condition for employing a simpli fi ed equation of state to achieve high accuracy.Moreover,numerical simulations performed by ANSYS/LS-DYNA software are conducted to validate the results through shock polar methodology.The results of this paper could be helpful for the decision of the equation of state on the oblique shock wave re fl ection in solids.

oblique shock wave re fl ection,shock polar,equation of state,solid

O357.4+2

A

10.6052/0459-1879-17-015

2017–01–09收稿，2017–08–23 录用,2017–08–23 网络版发表.

1)国家自然科学基金资助项目(11602027).

2)于鑫，研究员，主要研究方向：爆炸与冲击动力学.E-mail:yummuy@iapcm.ac.cn

黄萧,于鑫.不同状态方程对固体介质中斜激波反射的影响.力学学报,2017,49(5):1145-1153

Huang Xiao,Yu Xin.E ff ects of di ff erent equations of state on the oblique shock wave re fl ection in solids.Chinese Journal of Theoretical and Applied Mechanics,2017,49(5):1145-1153