高速列车头型长细比对气动噪声的影响1)

安 翼 莫晃锐 刘青泉

∗(中国科学院力学研究所流固耦合系统力学重点试验室，北京100190)

†(北京理工大学宇航学院力学系，北京100081)

高速列车头型长细比对气动噪声的影响1)

安 翼∗莫晃锐∗刘青泉†,2)

∗(中国科学院力学研究所流固耦合系统力学重点试验室，北京100190)

†(北京理工大学宇航学院力学系，北京100081)

高速列车的头尾车外形对气动噪声具有重要的影响.工程实践中随着车速的增加，车辆头部越来越细长，日本高速磁悬浮列车实践中甚至出现了具有极端长细比的头部形状.本文以讨论头型长细比对列车气动噪声的影响规律为出发点，应用非线性声学求解器(NLAS)和FW–H声学比拟法的混合算法，在3种运行速度下对基于CRH380A高速列车头型概化的4种不同头型长细比的模型车的气动噪声进行了数值模拟.给出了不同头型长细比列车的流场特征、气动阻力和气动噪声.结果表明，列车的气动总阻力随头型长细比的增大而减小，且头型长细比对列车总气动阻力的影响随运行速度的增加而增强.而头型长细比对气动噪声的影响呈现出较为复杂的影响，并不存在单调的影响关系；综合考虑气动阻力和气动噪声，长细比最大的头型综合性能较优，但差异并不显著，因此在不考虑微气压波等因素的条件下，简单增加车头长细比并不一定能带来明显的气动噪声性能提升.

高速列车，气动噪声，气动阻力，头型长细比

引言

近年来，我国的高速铁路迅速发展，已成为我国最主要的城际客运系统之一，更高速的磁悬浮列车也正在研发中.随着列车运行速度的不断提升，噪声问题日显突出，成为影响高速列车可持续发展的关键问题之一.高速列车的噪声主要由机械噪声和气动噪声组成[1]，气动声学理论指出，气动噪声的声功率与速度的6～8次方成正比[2]，而机械噪声则与速度的低次幂相关.研究表明[34]，当列车运行速度超过300km/h时，气动噪声将显著增强，并主导列车的总体噪声.高速列车的气动噪声主要来自于头尾车、转向架、受电弓和车体[5]，其中头尾车产生的气动噪声是其主要来源之一[6].Mellet等[7]分析了不同时速下的TGV-Duplex和ICE3高速列车的大量噪声实测数据，发现头尾车噪声占全车噪声的比重随着列车速度的提高而快速增长，当运行速度达到300km/h以上时，头尾车辐射的噪声超过其余八节车厢辐射的噪声，且头车的噪声比尾车噪声还要显著.由于高速列车头尾车的几何外形决定着周围流动的附着、边界层的发展和分离，以及列车尾部的流动分离和所产生的非定常尾流[8]，头尾车气动噪声的产生与其几何形状密切相关[9].

Kitagawa和 Nagakura[10]分析了日本新干线高速列车的气动噪声组成以及声源位置，发现光滑的车体表面可以有效地减少车体上部产生的气动噪声.Torii和Ito[11]对新干线列车噪声源的研究发现，对列车鼻形的改进可以降低标准测点处(距离轨道中心线25m，距地面高3.5m)约2dB(A)的噪声级，同时可有效减少列车在隧道中的压力波.Maeda等[12]和Ido等[13]通过风洞实验进行了一系列长细比下的高速列车头型的气动阻力测试，发现列车的气动阻力随着头型长细比的增大而有效降低.喻华华[14]曾在不同来流速度条件下，对CRH380高速列车的5种备选头型的气动噪声进行了风洞测试，结果表明，在相同长细比条件下，当头型满足流线型设计要求时，其不同横截面形状的车鼻对列车总体气动噪声的影响较为有限.王成强等[15]应用基于NLAS(nonlinear acoustics solver)的CAA模拟方法对高速列车的气动噪声进行了数值模拟研究.潘忠和陆森林[16]发现表面声功率级和脉动压力级最大值都出现在鼻锥、雨刷器等表面曲率变化较大的部位.

高速列车的头车和尾车具有一致的外形设计，一般为复杂的三维曲面[17]，其横截面存在明显形状或面积变化的区段称为车鼻，通常由此确定了头型最主要的几何特性[18].车鼻外形由众多参数决定，为头型特征结构的气动噪声特性研究带来了困难，实际研究中，常定义车头鼻形部位长度与后部车身断面等效半径之比为头型的长细比[19]，其与车鼻横截面形状分布一起，成为头型设计的重要参数.实践中，日本在 2015年试验的下一代磁悬浮列车L0系采用了长达15m的车鼻，而其车厢断面仅为3.1m×2.9m，长细比高达8.8，对列车功能和使用模式的设计都产生了影响.而在我国高速磁悬浮列车发展中，长细比在气动外形设计中的位置也是一个值得思考的问题.

高速列车头型的长细比对列车气动性能有着显著的作用和影响，然而，至今关于头型长细比对列车气动噪声影响的研究还较少，仍缺乏深刻的规律性认识.为此，本文将通过数值模拟方法，以我国自行设计的CRH380A高速列车为对象，参考飞行器设计中的优化技术[2022]，针对特定的车鼻横截面形状函数，探讨其分布区间的改变，即头型长细比的变化，对不同运行速度下高速列车气动噪声的影响，以期为合理进行头型降噪设计提供科学依据.

1 数值模拟方法

1.1 总体方法

本文采用计算流体力学/计算气动声学 (hybrid CFD/CAA)的混合方法对高速列车的气动噪声进行数值模拟.将计算区域分为非线性声源区(近场流动区)和线性声传播区，分别采用相应的计算方法求解.虽然大涡模拟(LES)和脱体涡模拟(DES)类方法以及FW-H方法已经逐渐用于噪声计算[23]，但其计算量很大.考虑到本文研究对象为细长流线体，其流动的不稳定性较弱，本文选用由Batten等[24]提出的计算量较低的非线性声学求解器(non-linear acoustics solver,NLAS)作为近场流动的求解算法.即首先使用cubic k-ε RANS模型求解Navier-Stokes方程，获得流动的统计定常解，然后运用非线性声学求解器(NLAS)求解流动的非定常时空演化和压力脉动，获得近场流场和噪声声源信息.而对于远场噪声的预测则采用声比拟法实现，即采用FW-H方程[25]，通过在控制面的积分得到远场噪声.由于近场部分求解的是脉动量，避免了LES等方法直接使用流动量造成的数值误差，同时对流项影响较小，NLAS对网格的需求也远低于LES和DES等方法.

1.2 非线性声学求解器(NLAS)

非线性声学求解器是由Batten等[2627]提出的一种求解统计定常状态流动中声的产生与传播的数值算法，其控制方程是从Navier-Stokes方程的扰动推导而来，称之为非线性扰动方程(NLDE)[24]，其形式为

式中，ρ为密度，u为速度，e为能量，τ为切应力，p为压强，δ为delta函数.

忽略密度扰动，对上述方程组取时间平均，可以消去时间演变项和所有线性通量项，得到

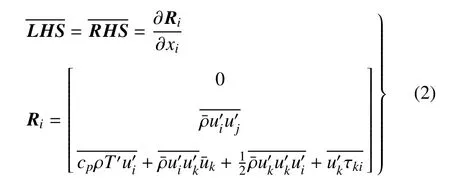
其中，Ri中的物理量对应于标准雷诺应力张量和湍流的热通量项，通过RANS方法可以求得这些未知项.

1.3 FW-H声学比拟法

远场声压的预测基于Farassat[28]给出的FW-H方程的时域积分解

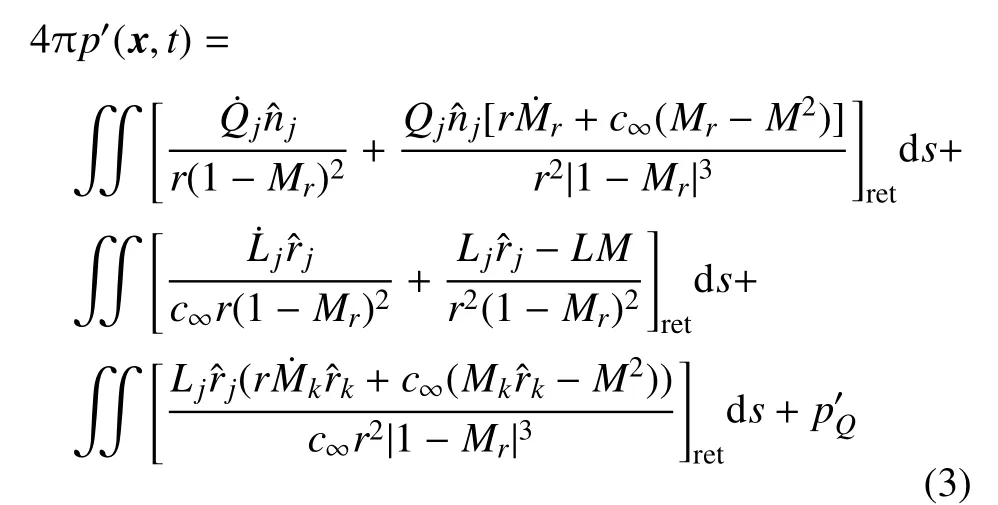
这里，Qi=(ρ∞−ρ)vi+ρui，Li=pˆni+ρui(uj−vj)nj；ρ∞和c∞分别为远场未受扰动流体介质的密度和声速，ui和vi分别表示当地流体速度和物体表面速度；ˆni和ˆri分别为物面单位法向矢量n和单位发射矢量(x−y)/r在3个方向的分量，r=|x−y|为观测点与声源之间的距离，其中x和y分别表示观测点和声源的位置矢量.符号[]ret代表在延迟时间τ=t−r/c∞下取值，其中t和τ分别为声源发出声波的时间和声波到达观测点的时间；Mr=viˆri/c∞为声源与观测点方向上的马赫数.

1.4 数值方法验证

首先用经典的汽车后视镜噪声算例做验证.Hold等[29]和Siegert等[30]对放置于平板上的汽车后视镜简化模型的气动噪声进行了风洞实验.如图1所示，后视镜简化模型由1/2圆柱与1/4球体拼接组成，竖直放置于平板上，圆柱直径和高度以及1/4球体的直径均为0.2m.将圆柱的下底面圆心设为坐标原点，流场中设置了两个压力探点，探点a位于半圆柱下游表面的边缘，坐标为(0.0,0.117,0.085)，探点b位于下游尾流的平板表面处，坐标为(0.3978,0.0,0.14181).本文采用与Siegert[30]实验相同的后视镜模型及几何配置，运用非线性声学求解器(NLAS)数值计算后视镜简化模型的近场流动与压力脉动.

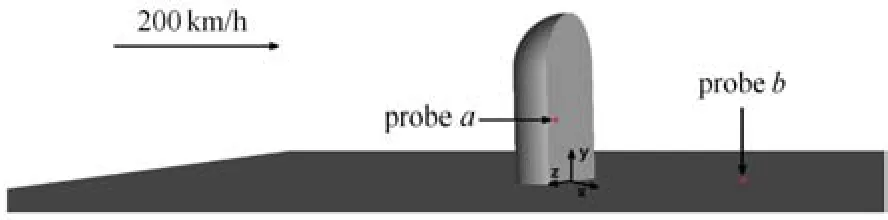
图1 放置在平板上的汽车后视镜简化模型及压力探点分布Fig.1 The geometrical model and probe points location of the simpli fi ed wind mirror test case

采用六面体结构网格离散求解空间，流动求解域范围为 x ∈ [−5D,15D]，y ∈ [0,10D]，z ∈[−5D,5D]，网格量约 4.9×105. 来流速度 U∞=200km/h，瞬态计算的时间步长△t=2×10−5s，约为5.6×10−3T0，其中，T0=D/U0≈ 3.6× 10−3s为流场以平均流速传播一个特征长度D所需的时间.数值求解时，后视镜模型和底部平板采用绝热的无滑移固壁条件，其它边界处为来流速度200km/h、参考温度298.5K和参考压力99530Pa的远场边界条件.计算可解析的信号最高频率 fmax=1/(2∆t)=25000Hz.

图2为探点a与探点b处声压级的数值计算结果与Siegert实验结果的对比.结果显示，在探点a处，数值结果低估了约40～400Hz频段内的声压级，但其余频段的声压级与实验结果吻合很好；而在探点b处，数值计算结果与实验结果在40～2000Hz的频段内整体上有着较好的吻合，在60～100Hz频段处，NLAS较为理想地预测了探点b处声压谱的峰值特征，但峰值频率的预测结果较实验结果偏低，整体上数值结果和实验测量结果符合良好.

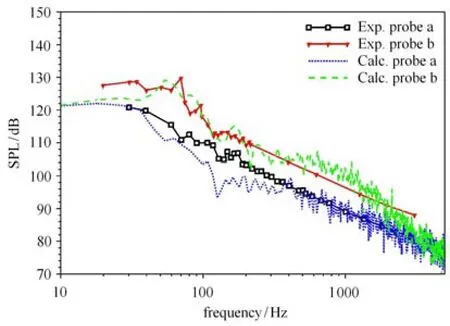
图2 探点a与b处声压级的数值结果与实验结果的对比Fig.2 Comparison of the calculated and experimental SPL values at the probe points

其次应用在同济大学的气动--声学风洞中开展的1:8模型试验结果做验证[14].该风洞在喷口速度160km/h试验段背景噪声SPL(A)为61dB，截止频率为50Hz.模型试验使用CRH 380A三编组模型，为突出头型影响，去除转向架并将其和车厢连接处填充光滑.试验中测点在距模型7.5m处平行于车长方向布置，有4组测点采集了噪声数据，试验共研究了200,230和250km/h三种风速.本文对三种风速条件下的噪声频谱和分布进行了研究，典型工况(250km/h，中间测点)的计算和试验测量结果的比较如图3所示.图中可以看出，模拟结果和试验测量结果在200Hz以上区域吻合良好，低频部分有差异.差异可能主要由风洞低频背景噪声所引起，但总体上在列车噪声所关注的频率范围，本文的数值方法给出了较好的结果.总体上验证了所采用数值方法的有效性和准确性.

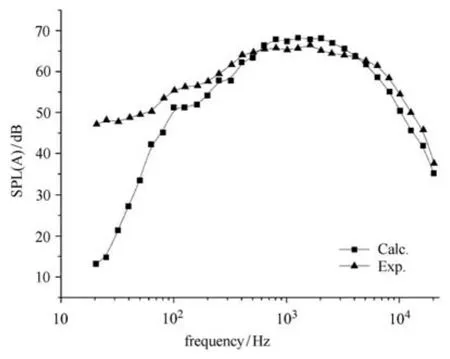
图3 250km/h条件下CRH380A缩尺模型典型测点噪声频谱数值模拟和测量结果的比较Fig.3 Comparison of the calculated and experimental SPL values for the 1:8 scaled CRH380A model in the wind of 250km/h

2 物理模型及计算条件

2.1 物理模型

基于CRH380A高速列车的基本头型，抽象简化出代表列车主体结构特征的细长结构体，作为本文研究的列车几何模型，模型列车为头车、单节中间车厢和尾车组成的三节车体编组.由于车体复杂部件对流场有一定影响[3132]，本文去掉车厢间隙、受电弓和转向架等非光顺曲面结构以突出头部形状的影响，并将CRH380A高速列车的车鼻横截面形状作为初始的分布函数.

将列车车鼻看作是其二维横截面沿长度方向的分布，则可使用函数S(l)表征其形状，S(l)为距离车头鼻尖l位置处的横截面形状函数，设其相对应的面积为A(l)，其中，l∈[0,ln]，ln为车鼻长度，其一般应小于单节车体的总长度.当确定车鼻横截面形状函数S(l)和其分布区间[0,ln]后，头型的最主要几何外形即可确定，其长细比λ=ln/r，其中为头型后部断面的等效半径值.

为研究头型长细比对气动噪声的影响，采用了4种具有不同长细比的头型，它们对应的列车几何模型如图4.CRH380A的头型ln为12m，长细比λ0约为6.36，A,B,C,D四种列车模型对应的头型长细比分别为：λA=0.75λ0，λB=1.0λ0，λC=1.25λ0，λD=1.5λ0.

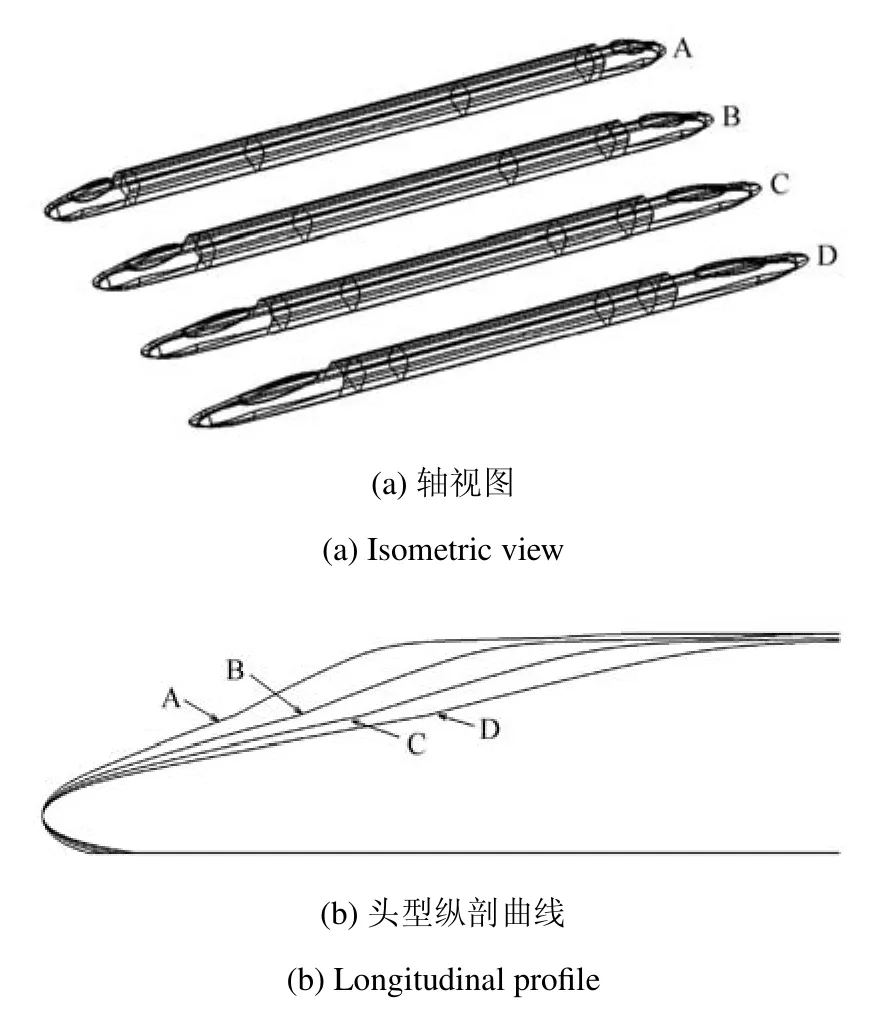
图4 4种头型细长比对应的列车几何模型Fig.4 Models of four trains with di ff erent slenderness ratio

2.2 计算区域与网格

简化列车模型的单节车体长Ls=26m，宽W≈3m，高 H≈3.5m，取列车下底面面心为计算域原点，从而车体长度在x轴上的范围为[−39m,39m].数值计算区域长度范围为 x∈[−4.5Ls,10.5Ls]，宽y∈ [−4Ls,4Ls]，高z∈ [−h,4Ls]，其中h=0.371m为车体底面距离地面的高度.

计算网格为四面体非结构网格，壁面附近区域的网格分辨率约为，在车体的尾流区域对网格进行了加密，当地网格分辨率约为.列车车体壁面边界层采用了棱柱网格，按照NLAS计算原理，第一层网格取在对数区，其高度对应的y+≈150，模型的计算网格总量约为5.8×106(见图5).

图5 求解空间的四面体非结构网格Fig.5 Unstructured mesh of the solving region

2.3 计算条件

数值求解时，列车车体为绝热的无滑移固壁条件，地面采用不可滑移的运动固壁条件，其运动速度与来流速度一致，其他边界处为参考温度298.5K和参考压力 101325Pa的均匀来流的远场边界条件.近场流动的非定常计算使用隐式的双重时间步(dualtime-stepping)方法，瞬态计算的时间步长∆t=5×10−5s. 计算可解析的信号最高频率 fmax=1/(2∆t)=10000Hz.

计算采用了250km/h,350km/h,500km/h三种运行速度，对应的马赫数 Ma分别为0.204,0.286和0.408.由于上述马赫数之间的差异较大，并处于弱可压缩区间，近场流动的数值求解统一采用了可压缩形式的控制方程，同时，通过预处理方法调节控制方程的Jacobi系数矩阵特征值u−c,u+c和u的大小，以减小声速u±c和流体质点速度u之间的差异，减少控制方程系数矩阵的特征值分散，使问题的刚性降低以提高收敛速度.

2.4 计算流程

求解过程中，首先使用cubic k-ε RANS模型求得流动的定常解，进行脉动重建后运用非线性声学求解器(NLAS)进行非定常流动演进，并在预设噪声面上采集压力脉动.在这一求解步，开始收集声源信息之前流动经过了额外的0.5s的非定常演变，以消除脉动重建所造成的人为影响，获得统计稳定的非定常流动.随后，在时间上继续推进0.5s以便在噪声面上记录近场流动的压力脉动，脉动信号的采集时长足够FW-H远场积分的需求.最后进行压力脉动的FW-H积分以获得远场兴趣点处的噪声信息.

3 计算结果及讨论

3.1 流速场与流动形态特征

流场特征决定了列车的气动噪声，为此我们首先分析了列车周围的流场特征.结果显示不同模型在不同速度下的流场表现出基本相似的特征.图6所示为B头型在350km/h运行速度下，列车周围流场不同剖面的流线.流线使用当地流向速度U与自由来流速度U∞的差值∆U进行渲染，为清晰对比当地流向速度与自由来流速度的相对大小，将速度差∆U的取值范围限定在[−10m/s,10m/s]的区间中.

图6 列车车体周围流场的流线形态，由∆U=U−U∞着色渲染Fig.6 Flow fi eld around the train,rendered with∆U=U −U∞

可见，在列车头车位置，流体从鼻尖驻点沿车鼻表面开始加速，且车鼻近地表面处的流体加速较快，在较短的距离内，当地流体的流向速度便超过了来流速度.而在车鼻表面的其他位置，流体随着曲面截面的扩张不断加速，并在车鼻截面达到最大时达到了局部的最高速度，随后，流体沿着具有固定截面形状的车体发展，当地流向速度趋近于来流速度.当流动发展到尾车附近时，车体上表面流体在尾车车鼻顶部存在加速段，随后速度快速下降，进入尾流区.在车体后部的两侧位置，靠近车体表面的流体流向速度在较长距离内都低于来流速度，它们与车体上表面的流体一起，汇聚进入车体尾部的尾流.

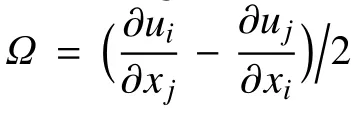
图 7为运行速度 350km/h时，不同头型长细比的列车周围流场的 Q判据等值面，Q的取值为(U∞/H)2，其中U∞=350km/h为来流速度，H≈3.5m为车体高度.Q判据等值面由当地压力p与来流压力p∞=101325Pa的差值∆p渲染和着色，为更清楚对比，∆p的取值限制在区间[−100Pa,100Pa]内.

根据图7所示的计算结果，4种车型的Q判据等值面具有相似的空间外形，主要存在于车体表面附近和尾流区域，由此可知，细长列车体流动中的主要声音产生区域为车体表面和尾流区.不同车型的Q判据等值面上的压力分布规律也具有一致性：头车车鼻位置具有高于来流压力的压力状态，随着流体沿着车鼻表面的加速流动，车鼻后部的流体速度高于自由来流速度，导致其当地压力低于自由来流的压力.随后，中间车体的压力逐渐趋于自由来流的压力值，当流体运动到列车尾部时，局部的加速导致当地压力快速下降，而当加速的流体进入尾流区域，其压力再次迅速上升.不同长细比的头型具有相异的车鼻长度和不同的截面变化率，导致当地流体的加速和减速状态存在差异，在压力分布上，表现为车头和车尾位置压力状态的空间差异.

图7 350km/h时的Q判据等值面，Q=(U∞/H)2，并由∆p=p−p∞着色渲染.自上而下分别为车型A，车型B，车型C，车型DFig.7 The iso-surface of the Q criterion(Q=(U∞/H)2)at 350km/h,rendered with∆p=p− p∞.From top to bottom:shape A,B,C and D

为了更清楚地了解列车周围的涡结构，图8给出了模型B尾流区域的Q判据等值面的局部视图.从中可以看出，列车尾流中存在明显的涡列对，并伴随着一系列的环状涡，环状涡从车体尾部开始发展，沿着尾流逐步扩张并随之破碎，尾涡结构的发展及破碎行为将产生可观的气动噪声.而尾涡中的压力分布整体上是从车体尾部向下游方向降低，逐步恢复到自由来流的压力状态，但其局部的压力状态是十分复杂的，比如，同一环状涡的不同位置，其压力值存在较大的差异.

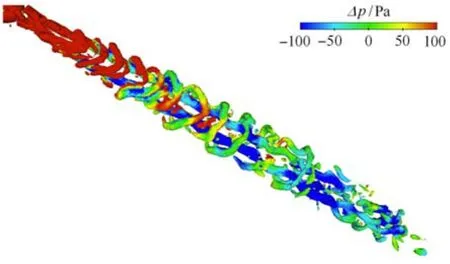
图8 来流速度为350km/h时，Q判据等值面描述的模型B的尾涡涡列，Q=(U∞/H)2，由∆p=p−p∞着色Fig.8 The tail vortex of the shape B at 350km/h,the iso-surface is determined by Q=(U∞/H)2,rendered with∆p=p− p∞

近场流动中压力脉动 p′的空间分布特征如图9所示，p′为各位置的瞬时压力p与时均压力¯p的差，即p′=p−¯p.从车体中纵剖面处的压力脉动灰度描述(图9(a))可知，列车表面的压力脉动呈现出沿车体表面正负压力交替分布的偶极子声源特性，而尾流区的压力脉动是在体空间内正负交替分布的，表现出四极子声源特性.图9(b)给出了近场压力脉动的三维空间描述，从中可以清晰地看出，列车表面和尾流中近场压力脉动在空间分布上的正负交替特征.

图9 列车(a)中纵剖面压力脉动p′=p−¯p的灰度描述,(b)Q=(U∞/H)2判据等值面处的压力脉动Fig.9(a)Pressure perturbation p′=p−¯p at the middle plane,(b)pressure perturbation at the iso-surface of Q=(U∞/H)2

3.2 气动阻力

图10 4种长细比头型的列车模型的阻力系数Fig.10 Drag coefficient of four trains with di ff erent slenderness ratio

高速列车头尾车外形的变化将影响周围流动的发展和分离，不仅影响列车的气动噪声，同样影响其气动性能，特别是阻力性能，列车气动噪声的优化不应以气动阻力的过度增加为代价.为此，分析了A,B,C,D四种列车模型在不同运行速度下的阻力系数，如图10所示.在三种运行速度下，头车和尾车阻力系数都随着长细比λ的增大而减小，这可能是由于长细比的增大，导致车鼻处的横截面变化率降低，从而使周围流动的稳定性增强，分离减弱.但头、尾车气动阻力的明显下降段发生在[λA,λC]区间，当λ＞λC时，头尾车阻力系数的下降趋势将显著减弱.中间车厢的阻力系数与头型长细比之间没有呈现出明确的规律，由于C型车与D型车在头尾车阻力上差异很小，而前者的中间车厢阻力系数较小于后者，从而C型车有着最小的总阻力.

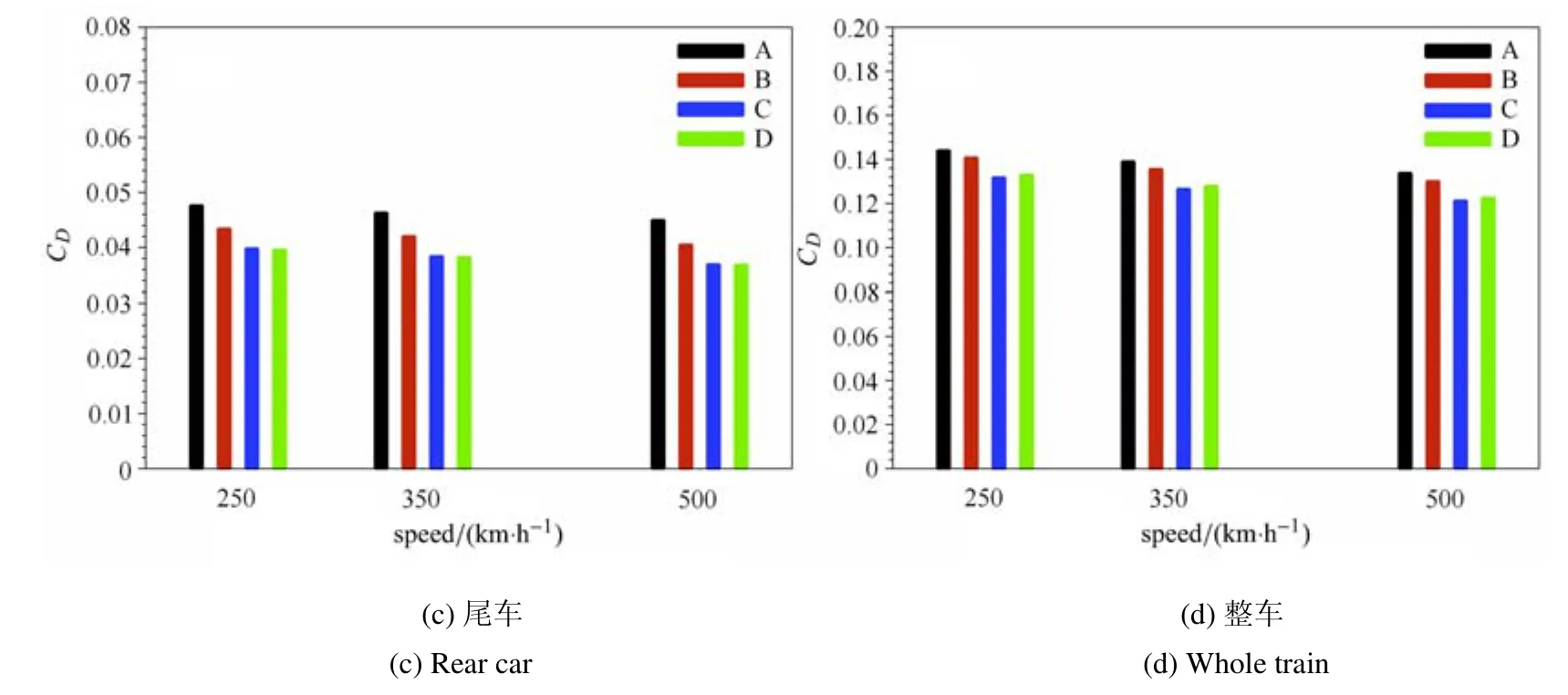
图10 4种长细比头型的列车模型的阻力系数(续)Fig.10 Drag coefficient of four trains with di ff erent slenderness ratio(continued)

与模型A相比，在250km/h的运行速度下，模型B,C,D的总阻力分别降低2.31%,8.56%,7.70%，在350km/h的运行速度下，总阻力分别下降2.50%,8.95%,8.01%，而在500km/h时，其总阻力分别下降2.81%,9.36%,8.45%.可见，在一定程度上，头型长细比增大有利于气动阻力的减小，但当长细比增大到一定程度时，气动阻力反而有所增大；而且头型长细比对列车气动阻力的影响随着运行速度的增加而增强.

3.3 远场噪声

远场噪声的求解基于近场声源面的 FW-H积分，由于湍动能的主要集中区域是气动噪声的主要声源区，本文选取最大湍动能的1%等值面作为近场声源面的参照，最终所选取的声源面位置如图11所示，声源面长度范围为[−45m,60m]，宽度为[−3m,3m]，高度区间为[0,5.5m].

高速列车铁路沿线噪声的评估通常基于距离轨道中心线25m、高度3.5m处的声压级，为探讨列车沿线的噪声特性，沿列车长度方向设置了如图12所示的声压探点，探点总数为13个，各探点在x方向上的间距为10m，从车头向车尾方向依次编号，其中P7探点与列车车体中点对齐.

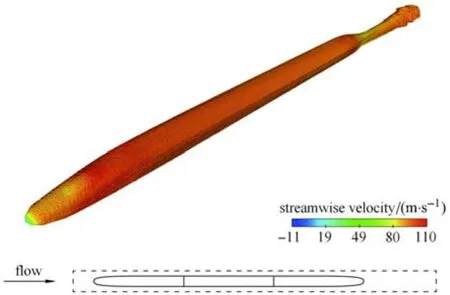
图11 FW-H声源积分面空间位置的选取.上方彩图：1%最大湍动能的等值面(由流向速度U渲染着色).下方虚线线框：作为FW-H积分边界的声源面的空间位置Fig.11 The integral surface for FW-H integral,top:the iso-surface of 1%turbulence kinetic energy rendered with stream velocity U,bottom:the wire frame shows the location of the actual used integral surface in the simulation

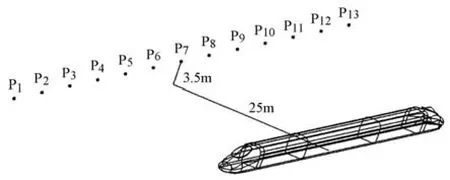
图12 列车长度方向的声压探点分布示意图Fig.12 The location of the sound pressure probes in the stream direction

图13为模型B的3个沿线探点P1,P7和P13在3种运行速度下的声压级频谱.可以看出，其气动噪声分布在很宽的频率范围内，并不存在明显的主峰，随着运行速度的提高，各探点位置的声压级在整个频段内都相应地增加.

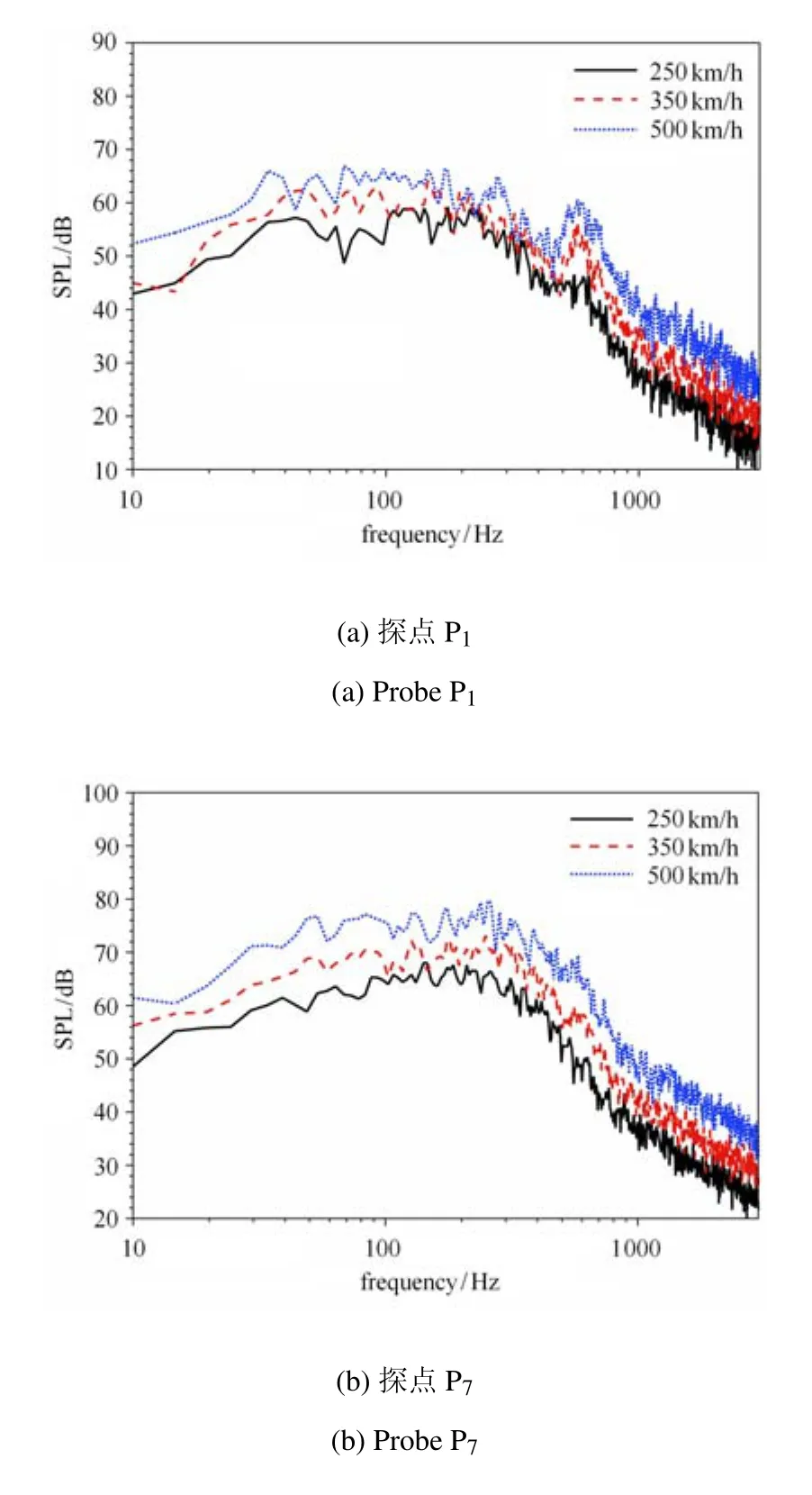
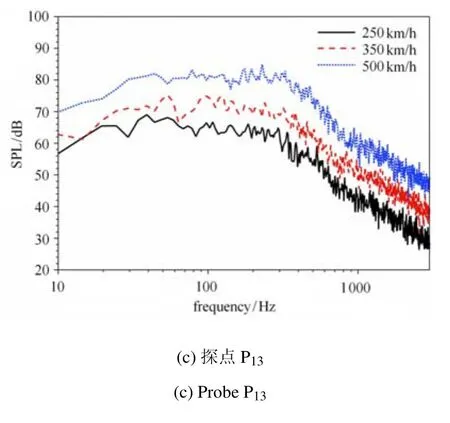
图13 模型B的3个沿线探点的声压级Fig.13 SPL of three probes for the case of shape B

4种车型的沿线噪声总声压级 (overall sound pressure level,OASPL)随运行速度的变化如图14，各型列车沿线噪声在车长方向上的分布具有相似的特征，列车的沿线噪声从车体前部向尾部方向上升，并且前部探点的总声压级趋于线性增长.随着运行速度的增大，各探点的总声压级相应增大，同时，越靠近车体尾部，探点的总声压级的增加幅度越大，这可能是由于速度的增大，使得列车后部产生了更高强度的尾流流动.

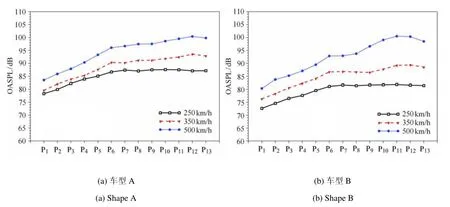
图14 4种车型沿线噪声总声压级随运行速度的变化Fig.14 The OASPL at di ff erent locations

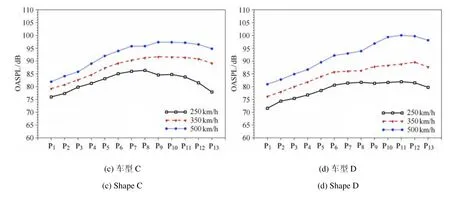
图14 4种车型沿线噪声总声压级随运行速度的变化(续)Fig.14 The OASPL at di ff erent locations(continued)

图15给出了列车沿线噪声总声压级与头型长细比之间的关系，总体上讲，4种头型中列车沿线噪声总声压级从高到低依次为A,C,B,D，且A与C具有相近的沿线噪声声压级，而B和D具有相近的声压级.同时，4种头型沿线噪声的差异随着运行速度的提高而减少，也就是说，头型对列车气动噪声的影响随着列车速度的增大而减弱.

图15 4种长细比头型的列车沿线噪声总声压级对比Fig.15 The comparison of the OASPL for di ff erent shapes

图16 沿列车周向分布的远场压力探点及相应的总声压级分布Fig.16 The OASPL distribution around the train

为更全面地比较头型对列车远场噪声声压级和方向性的影响，围绕列车车体设置了如图16所示的远场压力探点，探点位于距离地面3.5m的水平面内，沿半径为150m的圆周等间隔分布，间隔角度∆θ=15°，圆周的圆心与列车的中心具有相同的x和y坐标值.

沿列车周向分布远场压力探点的总声压级分布如图16所示，总声压级的圆周分布在列车两侧是对称的，声压级从高到低依次为A,C,B,D，其中，B和D的声压级在车头位置(θ=0°)存在小的差异，但在整个圆周上都是十分接近的，这与前面的沿线噪声结果一致.

4 结论

本文基于简化的列车细长体模型，在250km/h,350km/h,500km/h三种运行速度下，探讨了头型长细比分别为 0.75λ0，1.0λ0，1.25λ0和 1.5λ0四种头型的列车气动性能和气动噪声特性，得到如下主要结论：

(1)列车头尾车的气动阻力随着头型长细比的增大而减少，但当头型长细比超过其一定值后，其对气动阻力的影响将减弱；且头型长细比对列车总气动阻力的影响随运行速度的增加而增强.在本文研究中，C、D两种头型列车的头尾车气动阻力差异较小，整体上长细比为1.25λ0的C型车在四种车型中具有最低的气动总阻力.

(2)不同长细比的各型列车，其沿线噪声在车长方向上的分布具有相似的特征，列车的沿线噪声从车体前部到尾部逐渐上升，并且前部探点的总声压级趋于线性增长.随着运行速度的增加，各探点的总声压级相应增大，同时，越靠近车体尾部，探点的总声压级的增加幅度越大.

(3)四种头型沿线噪声之间的差异随着运行速度的提高而减少，也就是说，头型对列车气动噪声的影响作用随着列车速度的增大而减弱.

(4)对列车沿线噪声和远场圆周噪声的分析表明，长细比最小的A型车的远场声压级最高，其次是车型C，也就是说，具有最优气动阻力的C并不具有最低的远场噪声.长细比为1.0λ0的B和1.5λ0的D在空间上具有十分接近的声压级分布，在车头等局部位置，D的总声压级略微低于B.

(5)综合考虑气动阻力和气动噪声，长细比最大的D型车综合性能较优，但差异并不显著，因此在不考虑微气压波等因素的条件下，简单增加车头长细比并不一定能带来明显的气动阻力和噪声性能提升.

1 David Thompson,et al.Railway Noise and Vibration:Mechanisms,Modelling and Means of Control.Amsterdam:Elsevier,2008

2 King WF.III.A precis of developments in the aeroacoustics of fast trains.Journal of Sound and Vibration,1996,193(1):349-358

3 杨国伟,魏宇杰,赵桂林等.高速列车的关键力学问题.力学进展,2015,45:201507(Yang Guowei,Wei Yujie,Zhao Guilin et al.,Research progress on the mechanics of high speed rails.Advances in Mechanics,2015,45:201507(in Chinese))

4 Talotte C.Aerodynamic noise:a critical survey.Journal of Sound and Vibration,2000,231(3):549-562

5 张军,孙帮成,郭涛等.高速列车整车气动噪声及分布规律研究.铁道学报,2015,37(2):10-17(Zhang Jun,Sun Bangcheng,Guo Tao,et al.Research on aerodynamic noise radiated from whole body surface of high-speed train and its distribution.Journal of the China Railway Society,2015,37(2):10-17(in Chinese))

6 张亚东,张继业,李田.高速列车整车气动噪声声源特性分析及降噪研究.铁道学报,2016,38(7):40-49(Zhang Yadong,Zhang Jiye,Li Tian,Research on aerodynamic noise source characterization and noise reduction of high-speed trains vehicle.Journal of the China Railway Society,2016,38(7):40-49(in Chinese))

7 Mellet C,L´etourneaux F,Poisson F,et al.High speed train noise emission:Latest investigation of the aerodynamic/rolling noise contribution.Journal of Sound and Vibration,2006,293(3):535-546

8 SunZX,ZhangY,YangGW.SurrogateBasedOptimizationofAerodynamic Noise for Streamlined Shape of High Speed Trains.Applied Sciences-Basel,2017,7(2):192

9 刘加利,田爱琴,杜健等.头部控制线形状对高速列车气动噪声的影响.中国铁路,2014,11:58-62(Liu Jiali,Tian Aiqin,Du Jian,et al.In fl uence of the head car control line shape on the aerodynamic noise of high speed train.Chinese Railways,2014,11:58-62(in Chinese))

10 Kitagawa T,Nagakura K.Aerodynamic noise generated by Shinkansen cars.Journal of Sound and Vibration,2000,231(3):913-924

11 Torii A,Ito J.Development of the series 700 Shinkansen train-set(improvement of noise level).Japanese Railway Engineering,2000,40(1)

12 Maeda T,Kinoshita M,Kajiyama H,et al.Aerodynamic drag of shinkansen electric cars(series 0,series 200,series 100).Railway Technical Research Institute,Quarterly Reports,1989,30(1)

13 Ido A,Iida M,Maeda T.Wind tunnel tests for nose and tail of train.RTRI Report JNR,1993,7(7)(in Japanese)

14 喻华华.高速列车气动噪声产生与控制的机理研究.[博士论文].北京：中国科学院力学研究所，2013(Yu Huahua.On the mechanism of generation and control of aerodynamic noise for highspeed trains.[PhD thesis].Beijing:Institute of Mechanics,Chinese Academy of Sciences,2013(in Chinese))

15 王成强,邢海英,郑继峰.基于CAA的高速动车组气动噪声仿真研究.华东交通大学学报,2015,32(1):9-15(Wang Chengqiang,XingHaiying,ZhengJifeng,Simulationstudyonaerodynamicnoise of the high speed trains based on CAA.Journal of East China Jiaotong University,2015,32(1):9-15(in Chinese))

16 潘忠,陆森林.高速列车外流场气动噪声数值模拟研究.重庆理工大学学报(自然科学),2016,30(5):8-14(Pan Zhong,Lu Senlin.Numerical simulation of aerodynamic noise for high-speed train in exterior fl ow fi eld.Journal of Chongqing University of Technology(Natural Science),2016,30(5):8-14(in Chinese))

17 Ding SS,Li Q,Tian AQ,et al.Aerodynamic design on high-speed trains.Acta Mechanica Sinica,2016,32(2):215-232

18 张亮,张继业,李田等.超高速列车流线型头型多目标优化设计.机械工程学报,2017,53(2):106-114(Zhang Liang,Zhang Jiye,Li Tian,et al.Multi-objective optimization design of the streamlined head shape of super high-speed trains.Journal of Mechanical Engineering,2017,53(2):106-114(in Chinese))

19 Lee JS,Kim JH.Approximate optimization of high-speed train nose shape for reducing micropressure wave.Structural and Multidisciplinary Optimization,2008,35(1):79-87

20 常兴华,马戎,张来平等.基于计算流体力学的“虚拟飞行”技术及初步应用.力学学报,2015,47(4):596-604(Chang Xinghua,Ma Rong,Zhang Laiping,et al.Study on CFD-based numerical virtual fl ight technology and preliminary application.Chinese Journal of Theoretical and Applied Mechanics,2015,47(4):596-604(in Chinese))

21 胡守超,崔凯,李广利等.基于实验设计方法的高超声速飞机前缘型线优化分析.力学学报,2016,48(2):290-299(Hu Shouchao,Cui Kai,Li Guangli,et al.Optimization and analysis of the leading edge shape for hypersonic airplanes based on doe methods.Chinese Journal of Theoretical and Applied Mechanics,2016,48(2):290-299(in Chinese))

22 李广利,崔凯,肖尧等.高压捕获翼前缘型线优化和分析.力学学报,2016,48(4):877-885(Li Guangli,Cui Kai,Xiao Yao,et al.Leading edge optimization and parameter analysis of high pressure capturing wings.Chinese Journal of Theoretical and Applied Mechanics,2016,48(4):877-885(in Chinese))

23 冯峰,郭力,王强.高亚声速湍流喷流气动噪声数值分析.力学学报,2016,48(5):1049-1060(Feng Feng,Guo Li,Wang Qiang.Numerical investigation of noise of a high subsonic turbulent jet.Chinese Journal of Theoretical and Applied Mechanics,2016,48(5):1049-1060(in Chinese))

24 Batten P,Ribaldone E,Casella M,et al.Towards a generalized non-linear acoustics solver.AIAA-2004-3001//10th AIAA/CEAS Aeroacoustics Conference.Manchester,United Kingdom,May 10-12(2004)

25 Ffowcs Williams JE,Hawkings DL.Sound generation by turbulence and surfaces in arbitrary motion.Philosophical Transactions of the Royal Society of London,Series A,1969,264:321-342

26 Batten P,Goldberg U,Chakravarthy S.Reconstructed sub-grid methods for acoustics predictions at all Reynolds numbers//AIAA Paper,2511,2002

27 Batten P,Enrico R,Chakravarthy S.Towards a generalized nonlinear acoustics solver//AIAA Paper,2004-3001,2004

28 Farassat F.Discontinuities in aerodynamics and aeroacoustics:The concept and applications of generalized derivatives.Journal of Sound and Vibration,1977,55(2):165-193

29 Hold R,Brenneis A,Eberle A,et al.Numerical simulation of aeroacoustic sound generated by generic bodies placed on a plate:Part I-prediction of aeroacoustic sources//AIAA paper,1999,20:40-60

30 Siegert R,Schwarz V,Reichenberger J.Numerical simulation of aeroacoustic sound generated by generic bodies placed on a plate:Part II-prediction of radiated sound pressure//AIAA paper,1999,20:62-72

31 Yu HH,Li JC,Zhang HQ.On aerodynamic noises radiated by the pantograph system of high-speed trains.Acta Mechanica Sinica,2013,29(3):399-410

32 Guo DL,Shang KM,Zhang Y,et al.In fl uences of affiliated components and train length on the train wind.Acta Mechanica Sinica,2016,32(2):191-205

STUDY ON THE INFLUENCE OF THE NOSE SLENDERNESS RATIO OF HIGH-SPEED TRAIN ON THE AERODYNAMIC NOISE1)

An Yi∗Mo Huangrui∗Liu Qingquan†,2)∗(LMFS，Institute of Mechanics，Chinese Academy of Sciences，Beijing 100190，China)
†(School of Aerospace Engineering，Beijing Institute of Technology，Beijing 100081，China)

In the high-speed train design,the nose shape is a crucial control factor in fl uencing not only aerodynamic performance but also the aerodynamic noise.In the engineering practice,the nose shape becomes more and more slender along with the increasing of the design speed,e.g.the Japanese high-speed maglev train L0 series even has a 15m long slender nose(the slenderness ratio reach to 8.8).This study aims to discuss the in fl uence of the slenderness ratio of the nose shape on the aerodynamic noise.The hybrid numerical method of nonlinear acoustics solver(NLAS)and Ffowcs Williams-Hawkings(FW-H)acoustic analogy method is employed to study the aerodynamics noise characteristics.The numerical method is validated with a standard wind mirror test case and a set of acoustics wind tunnel experiments of the CRH380A train.The shape of the CRH380A train is chosen as a bench mark,and four di ff erent nose shapes of di ff erent slenderness ratio under di ff erent running speed situation are studied with numerical simulation.The fl ow fi eld,aerodynamic drag,and the aerodynamic noise are obtained and discussed.The result shows that the total drag decrease with the increase of the slenderness ratio,and this e ff ect enhances when the train speed increases.However,the in fl uence of the slenderness ratio on the aerodynamic noise is much complex as no simple trend is observed.Considering both the aerodynamic and aeroacoustics characteristics,the train with the most slender nose shape is the best while this advantage is not notable compared with the second-best.Thus,simply increase the slenderness does not necessarily result in better aerodynamic noise performance if the e ff ect of tunnel boom is not considered.

high-speed rail，aerodynamic noise，aerodynamic drag，slenderness ratio

O354.1,TB533+.2,U260.16,U266

A

10.6052/0459-1879-17-126

2017–04–17收稿，2017–08–11 录用,2017–08–20 网络版发表.

1)中国科学院知识创新工程方向性资助项目(KJCX2-EW-L02-1).

2)刘青泉，教授，主要研究方向：环境流体力学.E-mail：liuqq@bit.edu.cn

安翼,莫晃锐,刘青泉.高速列车头型长细比对气动噪声的影响.力学学报,2017,49(5):985-996

An Yi,Mo Huangrui,Liu Qingquan.Study on the in fl uence of the nose slenderness ratio of high-speed train on the aerodynamic noise.Chinese Journal of Theoretical and Applied Mechanics,2017,49(5):985-996