费雷特法在交通量分布预测中的应用

郑 强，冯学忠

（1.山西省交通规划勘察设计院，山西 太原030012；2.朔州高速公路有限公司，山西 朔州036000）

近年来交通量预测基本运用专业性地理信息系统软件TransCAD，采用“四阶段法”，建立交通规划模型，将各种交通运输数据综合运算，完成交通量的发生吸引、方式划分、交通分布及分配工作。预测者对各种数学模型运算过程未必做到深入了解，从多年公路工程可行性报告编制工作经历来看，费雷特法在交通量分布预测中能深入推演模型内在运算细节，即可更准确地标定、调整、修正模型参数，有效提高软件的预测精准度，提供可信度较高的量化依据。

1 交通量分布预测及费雷特模型

1.1 交通量分布预测

交通量分布预测是“四阶段法”交通量预测过程中重要阶段，是根据各交通分区发生、吸引量及公路交通分担量，在满足各小区将来发生和吸引交通量的前提下，按标定的分布模型，推算未来区间交通出行量和各小区内交通出行量。交通量分布预测通常有两类方法：

a）现在状态法 用现在（OD）型式推算将来的OD分布。主要有均衡增长率法、平均增长率法、底特律法和费雷特法（Fratar）等几种模型形式，其中费雷特法应用较为广泛。

b）综合模式法[1]利用区域经济活动质量和交通出行阻抗情况，预测将来交通出行分布的一种方法。主要有基本重力模型及其变形模型，分为无约束、单约束、双约束重力模型。

1.2 费雷特模型原理

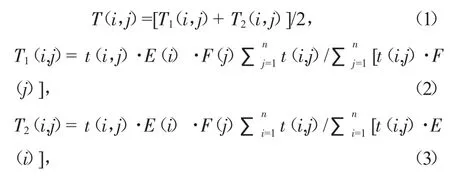
式中：T（i，j)为i区至j区的预测OD量；T1（i，j）为i区至j区的预测发生量；T2（i，j）为i区至j区的预测吸引量；t（i，j）为i区至j区的现状OD量；E（i）为i区的出行发生增长系数；F（j）为j区的出行吸引增长系数；n为全规划区域交通小区个数。

费雷特法认为两个交通小区之间的未来出行分布量不仅与这两个小区的增长系数有关，而且还与整个调查区内的增长系数有关，这较平均增长系数法有所改进，也更精确。它基于两个假设[2]：

a）未来的出行空间分布与i和j均成正比关系；

b）未来的出行空间分布与两地间的出行阻挠因素成反比关系，此处出行的阻挠因素可表示为（E（i）+F（j））/2。

费雷特法需用迭代方法反复修正和计算，直到收敛在误差[E′（i）F′（j）接近 1（允许误差 3%）为止]范围之内。费雷特法属于增长率法，其优点是模型思路明确，方便计算，可预测全部OD矩阵，稳定性较好，对于分布均匀，增长率变化不大，司机对比吸引力终点运行时间的地区较为合理。缺点是没有引入各个分区之间的交通阻抗因素。费雷特法适用于规划年内交通网络上阻抗变化不显著的出行分布问题，通常用于趋势交通量分布预测，交通分布是根据未来产生和吸引交通量的预测以及起讫点之间出行费用大小，来生成一个新的流量矩阵。

2 算例解析

某区域有3个交通小区，现状OD矩阵及通过出行产生预测所获得的各交通小区未来发生总量及吸引总量如表1，用费雷特法确定区域未来OD分布。

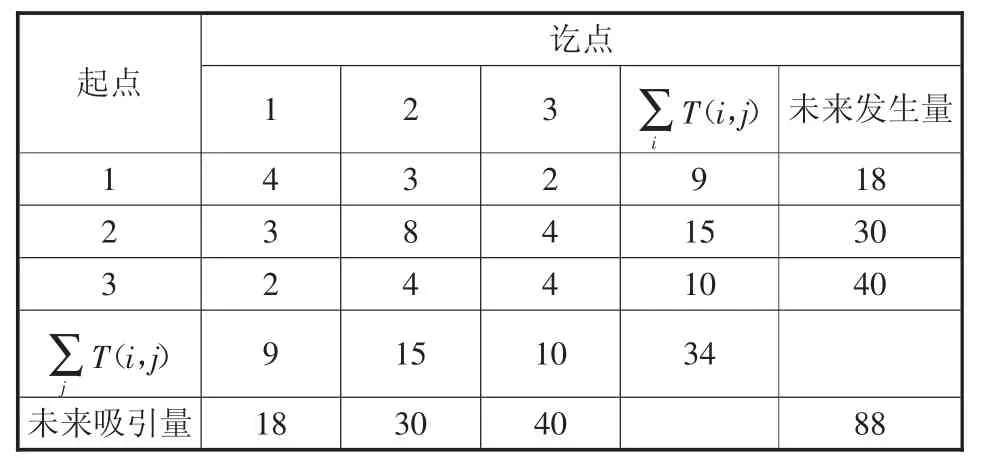
表1 现状OD矩阵及未来发生、吸引总量

解析：现状调查的OD矩阵为对称矩阵，且预测的各交通区发生量与吸引量相等，故各交通小区的发生增长系数与吸引增长系数相同，即：

经计算后，得表2所示的OD分布矩阵。在分布矩阵中，各交通小区修正的增长系数（接近1）已满足精度要求，无需进行迭代计算。可见费雷特模型的收敛速度较快，可节省运算时间。

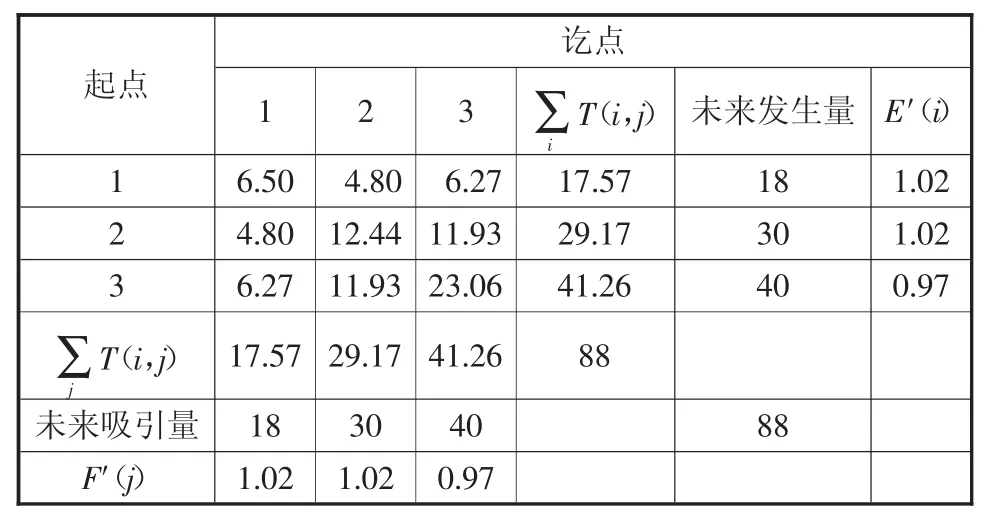
表2 费雷特模型预测的OD分布

3 结语

尽管实例现状OD表为对称矩阵，标定的各交通小区发生量与吸引量均等，各交通小区的发生与吸引增长系数也相同，经计算后，增长系数即满足精度要求，无需再次迭代计算。但笔者初衷是通过实例分步推演，从细节上直观认识演算过程，从理论真正理解费雷特法内涵意义。在实际工作中，无论何种形式的现状OD矩阵，均可采用此推演方法步骤及参数修正，将软件计算和重要细节验算两方面结合互动，全面提高交通量分布预测的精确度，为决策者提供更加科学可行、可靠的数据。