两条单生产商单零售商供应链的选址与定价竞争研究
徐 兵,张 斌,王 萍
(南昌大学 管理学院,南昌 330031)
两条单生产商单零售商供应链的选址与定价竞争研究
徐 兵,张 斌,王 萍
(南昌大学 管理学院,南昌 330031)
基于“线性市场”与线性运输成本的Hotelling模型,研究两条由单生产商单零售商组成的供应链的选址与定价竞争,建立了两条供应链均为集中式供应链(II模式)、均为分散式供应链(DD模式)、一条为分散式供应链一条为集中式供应链(DI模式)的竞争均衡模型,给出了均衡解的存在条件和均衡解.研究表明:DD模式下两条供应链的定价与利润比DI模式高,而DI模式又比II模式高,所以供应链集中式决策不是利润最大化目标下的占优策略;两条供应链的成本之差影响到双方利润,低成本供应链具有竞争优势.最后,对3种模式进行了数值仿真,参照结果提出了管理建议.
供应链竞争;选址与定价决策;Hotelling模型;纳什均衡;多层规划模型
随着经济全球化和信息技术的快速发展,企业不得不面对国内外企业的全面竞争和降低成本、提高效率的双重压力,此时谁能率先构建起完整、优化、具有竞争力的供应链系统,谁就能在未来的实力比拼中取胜.例如,零售业巨头沃尔玛之所以能形成强大的竞争实力,背后实质是与全球优秀企业联接而成的独特的供应链体系.21世纪的竞争体现为企业所在的供应链之间的竞争.例如,电脑产品经历了产品、价格、产能、服务等的数量比拼,现正走向敏捷供应链的角逐.供应链链间竞争问题已引起业界和学界的高度重视.文献[1]研究了两条供应链均为分散式供应链和均为垂直整合供应链下的价格竞争;文献[2]研究了两条供应链在提供相同价格产品时的产品质量竞争,考虑了两条供应链均为集成式、均为分散式或一条为集成式一条为分散式3种决策情形;文献[3]研究了两条供应链在无协调情景、混合情景(仅有一条供应链采用协调策略)和协调情景3种情况下的产品质量和价格竞争均衡;文献[4]研究了需求波动下的两条供应链之间的库存竞争,讨论了当供应链采取集中控制和分散决策时的最优库存策略;文献[5]利用均衡分析方法研究两条供应链在货架展示量与价格方面的竞争,建立了两条供应链竞争的EPEC、MPEC和Nash均衡模型;文献[6]分析了集中式情景、分散式情景和混合式情景下两条闭环供应链的价格竞争;文献[7]针对确定性产品需求函数和废品回收函数,运用博弈论与均衡理论分析了两条供应链的回收再制造竞争以及竞争下的协调问题;文献[8]研究了网络外部性环境下的两条竞争供应链的数量竞争模型,分析了供应链纵向联盟的形成机制;文献[9]采用Stackelberg模型分析了知识流无协调、混合协调和协调3种情境下两条供应链竞争问题,研究表明知识流协调对每条供应链而言都是占优策略.
上述文献主要研究两条供应链的价格、质量、库存等方面的竞争[1-9],未涉及空间选址与产品水平差异化竞争问题.现实中,企业不仅需要考虑产品定价,也需要决定空间选址或产品定位.例如,同一商业街上经常看到美特斯邦威与唐狮的门店比邻而居互相竞争.Hotelling(1929)针对消费者均匀分布于线性市场,提出线性运输成本下研究两厂商选址与定价竞争的Hotelling模型[10].随后,学者对该模型进行了多方面的拓展与应用,如考虑二次运输成本形式[11]、消费者服从三角函数分布密度函数情形[12]、具有网络外部性的网络产品厂商的选址与价格竞争[13]等;文献[14]假定消费者对渠道偏好服从[0,1]均匀分布,运用Hotelling模型研究传统零售商和电子渠道零售商的博弈;文献[15]基于Hotelling模型,研究了“政府单一化”、“完全市场化”和“多元化竞争”3种医疗服务市场模式的运作特点及其市场效率.
但文献[10-15]仅涉及两个厂商,未从供应链角度考虑选址与定价问题.文献[16-17]针对一个生产商和两个零售商组成的供应链,利用Hotelling模型分析了两个零售商间的选址与定价博弈,分别给出了使两个零售商选择供应链最优选址与定价的带转移支付的批发价合同、批发价与选址约束组合合同形式,并分析了社会福利最大化问题.文献[18]基于二次运输成本和选址为外生变量的Hoteling模型,研究两个竞争的下游核心企业对各自的上游供应商的外包决策与利润分享问题,对比分析了两条供应链均为分散式结构、均为集中式结构、一条为分散式结构一条为集中式结构下的利润变化.
本文在文献[16-17]的基础上,研究两条由单生产商单零售商组成的供应链的选址与定价竞争问题,给出了两条供应链均为集中式供应链、均为分散式供应链、一条为集中式一条为分散式供应链下的竞争均衡存在条件及均衡解.文献[18]假定选址为外生变量及二次运输成本不同,本文假定选址是内生变量,运输成本为线性函数.
1 模型假设
设消费者在长度为l的“线性市场”上均匀分布,两条分别由生产商Mi和零售商Ri(i=1,2)组成、销售完全同质产品的供应链,进行3阶段完全信息博弈:两零售商同时决定市场选址,随后两生产商同时决定批发价,两零售商再决定产品进货量和售价,最后生产商按零售商的订货量给其供货,销售发生.需要说明的是,本假设中的“线性市场”可以是产品水平差异化特征的某个维度,消费者对此产品特征的偏好服从均匀分布,“选址”问题对应产品的定位,不一定是实际意义上的物理选址即不是战略决策问题.设生产商Mi给零售商Ri的产品批发价为wi,Ri决定的产品售价为pi,R1离市场左端点的距离为a,R2离市场右端点的距离为b,满足:0≤a≤l-b≤l,wi≥cMi,pi≥wi+cRi,其中:cMi是生产商Mi的单位生产成本;cRi是零售商Ri的单位销售成本.考虑线性交通成本,则距市场左端点x处的消费者到Ri处购物的成本为:
(1)
其中:t为单位交通成本.消费者以最小化购物成本来决定到哪个零售商处购物.假定每个消费者只购买单位产品,则R1的市场需求为[11]:
(2)

条件1两条供应链成本之差满足:-lt/2<Δc 完全信息下,零售商向生产商的订货量等于市场需求.记x1=a,x2=b,生产商Mi、零售商Ri和供应链i(i=1,2)的利润函数分别为: πMi(wi)=(wi-cMi)qi, (3) 2.1II模式下供应链竞争均衡模型 假设两条供应链均为集中式(II模式),即供应链i均以最大化整体利润为目标进行博弈.因批发价是供应链内部决策,此时两条供应链竞争均衡问题为如下两层规划模型: (6) 其中:上层是两条供应链的选址竞争的Nash均衡;下层是两条供应链的定价竞争的Nash均衡.运用后退归纳法进行求解. 命题1II模式下两条供应链选址与定价竞争均衡存在的充要条件为: (7) (8) 可得到式(8).但式(8)是最优解,需满足如下条件(其中ε是很小的正数): (9) 即两条供应链同时占有市场的利润比独占市场好.求解式(9)可得到式(7). 结论1两条集中式供应链将基于供应链成本进行加成定价,成本加成的大小取决于两条供应链的选址距离及成本之差.特别地,当c1=c2=0时,命题1的结论与经典Hotelling模型的结论一致[11](此时集中式供应链可视为一个实体). 由命题1,将式(8)代入供应链利润函数式(5),有: (10) 2.2DD模式下两条供应链选址与定价竞争均衡模型 当两条供应链均为分散式供应链时,各成员企业均以最大化自身利润为目标进行决策,二者的选址与定价竞争均衡问题为如下3层规划模型: (11) 其中:第一层是两个零售商的选址竞争均衡;第二层是两个生产商的批发价竞争均衡;第三层是两个零售商的定价竞争均衡.运用后退归纳法进行求解. 引理1DD模式下两个零售商的选址与定价竞争均衡存在的充要条件为: (12) (13) 引理1的证明与命题1类似,只需将wi代替cMi(i=1,2),因篇幅所限,故省略证明过程. 结论2两条分散式供应链中零售商将基于零售商总成本(含进货与销售成本)进行加成定价,成本加成的大小取决于两个零售商的选址距离及成本之差. 命题3DD模式下两条供应链选址与定价竞争均衡存在的充要条件为: (14) (15) (16) 证 由引理1,将式(13)代入生产商利润函数式(3),有: 可得到式(15),将其代入式(12)和(13),可得到式(14)和(16). 由命题3,将式(16)代入零售商的利润函数式(4),有: (17) 特别地,当c1=c2=c时,有: 2.3DI模式下两条供应链选址与定价竞争均衡模型 假设供应链1为分散式供应链、供应链2为集中式供应链(相反的情况可由对称性得到)(DI模式),两条供应链的选址与定价竞争均衡问题为如下3层规划模型: (18) 其中:第一层是R1与供应链2的选址竞争均衡;第二层是M1的利润最大化问题;第三层是R1与供应链2的定价竞争均衡.运用后退归纳法进行求解. 引理2DI模式下零售商R1与供应链2的选址与定价竞争均衡存在的充要条件为: (19) (20) 引理2的证明与命题1类似,只需将w1代替cM1,因篇幅所限,同样省略证明过程. 结论3DI模式下,分散式供应链中零售商将基于零售商总成本(含进货与销售成本)进行加成定价,集中式供应链将基于供应链总成本进行加成定价,成本加成的大小取决于二者的选址距离及成本之差. 命题5DI模式下两条供应链选址与定价竞争均衡存在的充要条件为: (21) (22) (23) 证 由引理2,将式(20)代入生产商M1的利润函数式(3),有: 可得到式(22),将其代入式(19)和(20),可得到式(22)和(23). 由命题5,将式(23)代入式(4)和(5)得到R1与供应链2的利润函数: (24) 命题6DI模式下两条供应链进行对称选址(a=b)与定价竞争,竞争均衡解与供应链利润为: 特别地,当c1=c2=c时,有: 2.4静态均衡分析 在式(7),(14),(21)成立的情况下,对比式(8),(16)和(23),有: 进一步,将式(8),(16)和(23)代入供应链利润函数式(5),有: 结论4两条供应链进行选址与定价竞争,DD模式下两条供应链的定价与利润比DI模式高,而DI模式下两条供应链的定价与利润比II模式高,即: 结论4与一般文献中“集中式供应链的利润一定比分散式供应链高”的结论完全相反,也即集中式决策并不是两条供应链选址与定价竞争下的占优策略.例如,两条成本相同的供应链(c1=c2=c)进行对称选址(a=b)与定价竞争,有: 结论5两条供应链进行选址与定价竞争,两条供应链的利润都将随着市场规模l和产品水平差异化程度t的增加而增加;随两条供应链成本之差的增大,高成本供应链的利润将下降,而低成本供应链的利润将增加. 将式(8),(16)和(23)代入式(2),有: 结论6表明,两条供应链竞争下,不管对方供应链是分散式供应链还是集中式供应链,我方供应链采取集中式控制都是市场份额最大化目标下的占优策略.但由结论4可知,集中式控制并不是利润最大化目标下的占优策略. 以线性市场上某家用小电器为例,进行调查和统计数据分析,得到模型参数:l=1600,t=0.01,cR1=8,cM1=80,cR2=10,cM2=84,此时c1=88,c2=94,ΔcM=4,ΔcR=2,Δc=6.为分析方便,考虑对称选址的情况.采用matlab编程求解模型式(6),(11)和(18),得到DD、DI、II3种模式下各方决策与利润(表1). 表1 两条竞争供应链对称选址下3种竞争均衡模式Tab.1 Three competitive equilibrium models in two competitive supply chains under symmetric location 根据表1,进行模型结果分析. (1) II、DI、DD模式下两条供应链的产品定价与利润依次递增,表明结论4的正确性; (2) 两条供应链进行选址与定价竞争,供应链集中式决策不是占优策略.例如,两条分散式供应链(II模型)中供应链2转而采取集中式控制(DI模式)时,反而使两条供应链的利润均有所下降(55555.6→16200.0,47022.2→26450.0);当DI模式下供应链1由分散式决策转而采取集中式决策方式(II模式)时,使对方供应链利润下降,但自身利润并未提升(16200.0→16200.0,26450.0→9800.0).所以,本文结果与一般文献中“集中式决策将提升供应链利润”的结论完全相反. (3) 集中式控制下产品售价较低,消费者将获得更大福利. 由命题1~4、结论1~6及数值仿真结果,可提出如下管理对策: (1) 两条供应链进行选址与定价竞争,集中式不是占优策略,所以供应链管理者应允许成员在规则范围内各司其职、结合自身利润来制定决策; (2) 供应链管理者应加大宣传,提升产品的市场规模,通过扩大需求来增利; (3) 供应链管理者应扩大产品水平差异化程度,使消费者愿意支付高价格,通过高价获得高收益; (4) 供应链管理者应该控制供应链运作成本,以在供应链竞争中获得更竞争优势. (5) 对于药品、盐等生活必需品,政府应给予必要的选址约束和限价,以提高社会福利. 针对线性市场上两条供应链的选址与定价竞争,运用Hotelling模型与博弈论方法建立了II、DI、DD3种模式下的竞争均衡模型,给出了均衡解的存在条件及其均衡解,最后进行了数值仿真,提出了管理对策.研究表明:两条供应链选址与定价竞争下,集中式决策不是利润最大化目标下的占优策略;两条供应链成本之差对双方利润均匀影响,低成本供应链具有较大的竞争优势. 本文仅研究了产品同质与线性运输成本下两条供应链的选址与定价.未来可结合产品质量差异、消费者不均匀分布[12]、网络外部性[13]、多销售渠道[14]、非线性运输成本[19]等情况,研究两条供应链的选址与定价竞争,将得到更有意义的结论.例如,在二次运输成本下考虑两条供应链的选址与定价问题,此时零售商将会向市场两端定位,即采取最大化产品差异的策略,不会出现本文中向市场中心靠拢的现象. [1] ANDERSON E J,BAO Y.Price competition with integrated and decentralized supply chains [J].EuropeanJournalofOperationalResearch,2010,200(1):227-234. [2] XIE G,WANG S Y,LAI K K.Quality improvement in competing supply chains [J].InternationalJournalofProductionEconomics,2011,134(1):262-270. [3] 鲁其辉,朱道立.质量与价格竞争供应链的均衡与协调策略研究 [J].管理科学学报,2009,12(3):56-64. [4] 肖迪,黄培清,顾锋.需求不确定条件下供应链之间的库存竞争策略 [J].上海交通大学学报(自然科学版),2008,42(9):1511-1514. [5] 徐兵,孙刚.需求依赖于货架展示量的供应链链间竞争与链内协调研究 [J].管理工程学报,2011,25(1):197-202. [6] 孙嘉轶,姚锋敏,滕春贤.竞争闭环供应链的均衡结构选择模型研究 [J].中国管理科学,2015,23(SI):551-556. [7] 徐兵,杨金梅.需求与回收确定下闭环供应链的竞争与链内协调研究 [J].中国管理科学,2014,22(2):48-55. [8] 刘晓婧,艾兴政,唐小我.网络外部性下链与链竞争纵向联盟和收益共享合同 [J].预测,2016,35(4):75-80. [9] 杨晓艳,陈杰.两条供应链竞争下的知识流协调策略及其影响因素 [J].系统工程,2014,32(10):71-77. [10] HOTELLING H.Stability in competition [J].EconomicJournal,1929,39(153):41-57. [11] ASPREMONT C D,GABSZEWICZ J J,THISSE J F.On Hotelling’s stability in competition [J].Econometrica,1979,47(5):1145-1150. [12] 顾锋,黄培清,周东生.消费者不均匀分布时企业的最小产品差异策略 [J].系统工程学报,2002,17(5):467-471. [13] 徐兵,朱道立.具有网络外部性的扩展Hotelling模型 [J].管理科学学报,2007,10(1):9-17. [14] 谷泽昊,郭志芳,王文利.基于顾客渠道偏好改进的Hotelling模型的双渠道供应链零售商博弈 [J].工业工程,2015,18(1):77-83. [15] 浦徐进,何未敏.基于Hotelling模型的医疗服务市场发展模式研究 [J].预测,2016,35(4):57-62. [16] 徐兵,朱道立.零售商水平竞争下二层供应链协调策略设计 [J].管理工程学报,2009,23(4):54-58. [17] 徐兵,朱道立.零售商水平竞争分析与供应链协调策略设计 [J].系统工程学报,2010,25(5):609-615. [18] 杨道箭,白寅.基于Hotelling模型的供应链间核心企业竞争与分散式 [J].系统工程理论与实践,2015,35(12):3025-3037. [19] ECONOMIDES N.Minimal and maximal product differentiation in Hotelling’s duopoly [J].EconomicsLetters,1986(21):67-71. StudyoftheCompetitionofLocationandPricingbetweenTwoSupplyChainsEachConsistingofOneManufactureandOneRetailer XUBing,ZHANGBin,WANGPing (SchoolofManagement,NanchangUniversity,Nanchang330031,China) The competition of location and pricing of two supply chains(SCs) is studied by using Hotelling model with linear market and linear cost function.Each SC consists of one manufacture and one retailer.The competitive equilibrium models are built respectively when two SCs are centralized SCs(II mode),decentralized SCs(DD mode),or one decentralized SC and one centralized SC(DI mode).The existence conditions of equilibrium and the equilibrium solutions are obtained.The research results show that the product prices and profits of two SCs in DI mode are lower than those in DD mode,but are more than those in II mode.So,the centralized decision mode is not the dominant strategy for profit-maximization.The difference between two SCs will affect the profits of two SCs,and SC with lower cost has competitive advantage.Finally,a numerical simulation is put forward together with some management suggestions. supply chain competition; location and pricing decision; Hotelling model; Nash equilibrium; multi-level programming model 0427-7104(2017)05-0619-09 2016-11-13 国家自然科学基金(71561018,71502076);2015年江西省高校人文社会科学重点研究基地项目(江西省融入“一路一带”战略研究);南昌大学研究生创新项目(cx2016041,cx2016039) 徐 兵(1972—),男,博士,教授,E-mail:xu_bing99@sina.com. F274 A2 两条供应链选址与定价竞争均衡分析
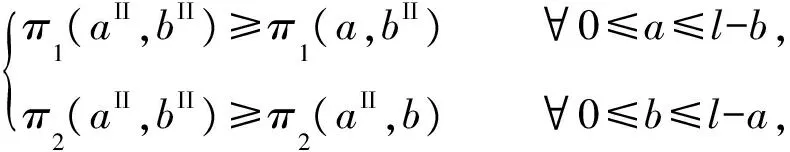
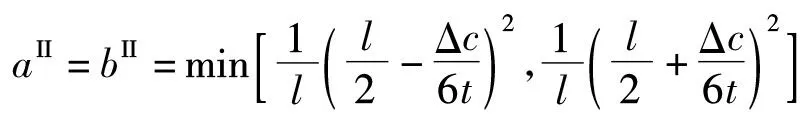


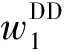



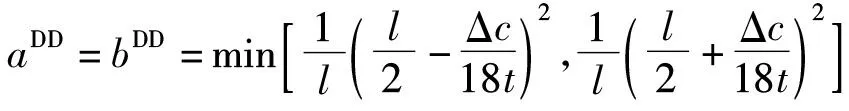
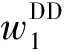
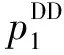
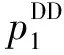
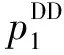
3 算例分析

4 结 语

