基于同伦摄动Sumudu转换法和Sumudu分解法求解非线性分数阶偏微分方程

尹伟石，韩 涛

(长春理工大学 理学院，长春 130022)

基于同伦摄动Sumudu转换法和Sumudu分解法求解非线性分数阶偏微分方程

尹伟石，韩 涛

(长春理工大学 理学院，长春 130022)

本文运用同伦摄动Sumudu转换法和Sumudu分解法求非线性分数阶偏微分方程的数值解，并对结果进行比较.两种方法计算过程简单，而且得到的近似解完全一致.

分数阶偏微分方程；同伦摄动Sumudu转换法；Sumudu分解法

分数阶微积分方程非常适合刻画具有记忆和遗传性质的材料和过程，其对复杂系统的描述具有建模简单、参数物理意义清楚、描述准确等优势，因而对分数阶微分方程的研究受到越来越多的关注.求解非线性偏微分方程比求解线性偏微分方程难度大，大多数非线性偏微分方程只能依靠数值解法.Adomian[1-2]提出了一种数值方法——Adomian分解法(Adomian Decomposition Method,ADM).该方法可以有效地解出一大类线性和非线性的，确定的或随机微分方程的近似解.Kumar等[3]提出了一种新方法，即Sumudu分解法(Sumudu Decomposition Method,SDM)求解非线性方程组，该方法将Sumudu转换法和Adomian分解法结合来求解问题.实验表明该方法是非常简单有效的，并且可以被应用到其他非线性问题.Ghorbani等[4]则解决并优化了Adomian分解法的求解困难问题.经Jafari等[5-6]补充完善后，Adomian分解法变得更加直接有效.摄动法[7-10]是使用最为广泛的解析近似方法，己经成功地解决了科学和工程中的许多问题.同伦摄动法是被He[11-12]第一次提出用来解决不同线性、非线性的初值和边值问题的一种新方法，非线性偏微分方程和积分方程都可以利用同伦摄动法求出近似解，并且可以使求解过程大为简化.大量的例子显示这种方法简单而有效.

本文将同伦摄动法和Sumudu转换法结合，提出同伦摄动Sumudu转换法(Homotopy Perturbation Sumudu Transform Method,HPSTM)来求解非线性分数阶偏微分方程，同时应用Sumudu分解法求解同问题作为验证，得到问题的完全一致的近似解.

1 分数阶微积分的基本定义

定义1(Riemann-Liouville分数阶积分定义)设f(t)在(0,+∞)上逐段连续，即f∈C(0,+∞)是在J=[0,+∞)的任何有限子区间上可积.对于t>0,α>0，称

(1)

J0f(t)=f(t).

由Riemann-Liouville分数阶积分可知

(2)

定义2函数f：[0,+∞)→阶数为α>0，Caputo分数阶导数是指

(3)

其中：m-1<α≤m,m∈；t>0.式(3)右边是在(0,+∞)上逐点连续的.

定义3(Sumudu转换)

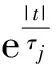
(4)

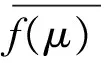
(5)

定义4(Caputo分数阶导数的Sumudu转换)

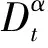
(6)

2 同伦摄动Sumudu转换法(HPSTM)

考虑一般的分数阶非线性非齐次局部微分方程

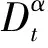
(7)

初始条件为

U(x,0)=f(x)，

(8)

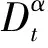
(9)

运用Sumudu转换的微分性质得

S[U(x,t)]=f(x)+uαS[g(x,t)]-uαS[RU(x,t)+NU(x,t)].

(10)

在式(10)两边进行Sumudu转换逆运算，可得

U(x,t)=G(x,t)-S-1[uαS[RU(x,t)+NU(x,t)]]，

(11)

其中G(x,t)代表源项和规定的初始条件.利用同伦摄动分析法可得

U(x,t)=G(x,t)-PS-1[uαS[RU(x,t)+NU(x,t)]]，

按摄动系数展开得

(12)

其非线性项可以被分解为

(13)

其中Adomian多项式An由下式给出：

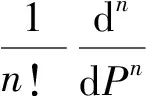
(14)

将式(12)，(13)代入式(11)，可得

(15)

式(15)结合了Sumudu转换法、同伦摄动法、Adomian多项式.比较P的系数可近似得到

P0：U0(x,t)=G(x,t)，

P1：U1(x,t)=-S-1[uαS[RU0(x,t)+A0]]，

P2：U2(x,t)=-S-1[uαS[RU1(x,t)+A1]]，

P3：U3(x,t)=-S-1[uαS[RU2(x,t)+A2]].

(16)

重复这个过程，Un(x,t)的其他部分也可以被求出.可以近似求出U(x,t)的分析解为

(17)

3 Sumudu分解方法(SDM)

下面用Sumudu分解方法求解分数阶非线性非齐次偏微分方程(7)，(8).

第1步，在式(7)两边运用Sumudu转换法(这里用S表示)，可得

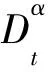
(18)

再运用Sumudu转化的微分性质得

S[U(x,t)]=f(x)+uαS[G(x,t)]-uαS[RU(x,t)+NU(x,t)].

(19)

在式(19)两边进行Sumudu转换逆运算，可得

U(x,t)=G(x,t)-S-1[uαS[RU(x,t)+NU(x,t)]]，

(20)

其中G(x,t)代表源项和规定的初始条件.

Sumudu分解法的第2步是给出作为一个无穷级数表示的解决方案：

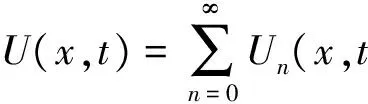
(21)

非线性部分可分解为

(22)

An是关于U0,U1,U2,…，Un的Adomian多项式，它可以通过下式计算：

(23)

将式(21)，(22)代入式(20)得

(24)

比较两边得到

U0(x,t)=G(x,t)，

U1(x,t)=-S-1[uαS[RU0(x,t)+A0]]，

U2(x,t)=-S-1[uαS[RU1(x,t)+A1]]，

U3(x,t)=-S-1[uαS[RU2(x,t)+A2]]，

…

(25)

递推关系为

Un+1(x,t)=-S-1[uαS[RUn(x,t)+An]]n≥0.

(26)

在式(26)的右侧运用Sumudu变换，再运用Sumudu逆变换，可以得到U0，U1,U2,…，Un的值.

4 数值例子

考虑时间-分数阶非线性微分方程：

(27)

初始条件为

U(x,y,0)=xy.

(28)

式(27)两边应用Sumudu转换得到

(29)

下面分别用同伦摄动Sumudu转换法和Sumudu分解法来求解问题(27)，(28).

4.1同伦摄动Sumudu转换法

进行Sumudu逆变换得到

根据同伦摄动法，我们构造以下同伦：

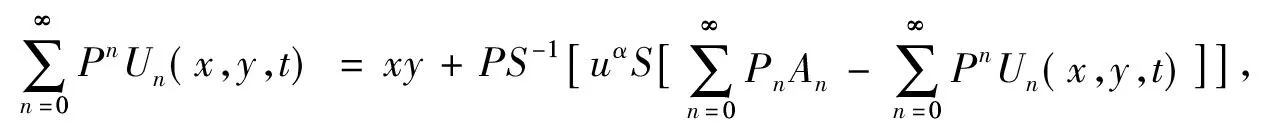
(30)

其中An是关于U0,U1,U2,…，Un的Adomian多项式，它可以通过下式计算：

(31)

所以

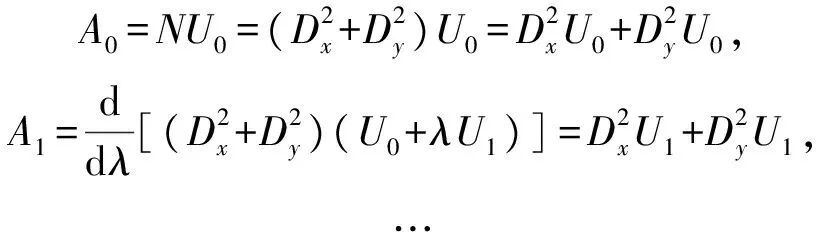
(32)

依次可求出U0,U1,U2,…，Un的每一项,比较式(30)两端系数得

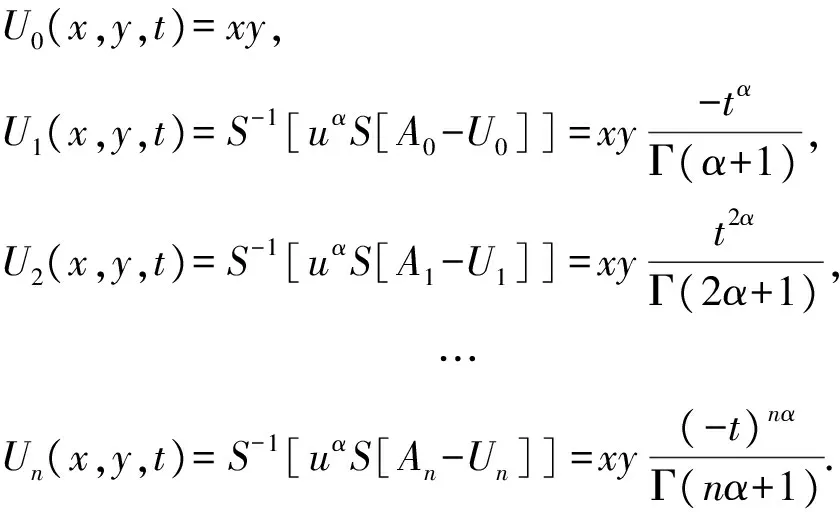
(33)

所以

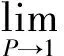
(34)

令α=2，则

4.2Sumudu分解法

根据同伦摄动法，有

(35)

所以

(36)

可化为

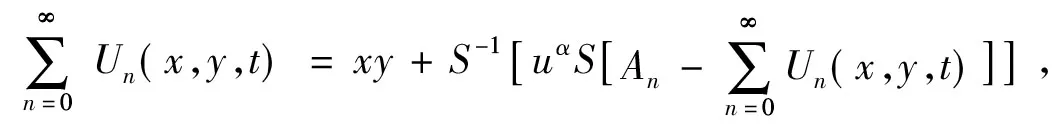
(37)

其中An是Adomian多项式的非线性项，前几项为

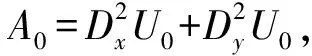
(38)

比较等式两边系数得

(39)

所以

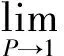
(40)

令α=2，则

同HPSTM的结果相同.

5 结 语

本文两种方法都在保证数值解精度的情况下大大减少了计算量，因此在求解一系列非线性分数阶局部微分方程分析解和数值解方面非常方便有效.

[1] ADOMIAN G.Solving frontier problems of physics：The decomposition method [M].Boston,Mass，USA：Kluwer Academic Publishers,1994.

[2] ADOMIAN G,SERRANO S E.Stochastic contaminant transport equation in porous media [J].AppliedMathematicsLetters,1998,11(1)：53-54.

[3] KUMARD,SINGH J,RATHORE S.Sumudu decomposition method for nonlinear equations [J].InternationalMathematicalForum,2012,7(11)：515-521.

[4] GHORBANI A,SABERI-NADJAFI J.He’s homotopy perturbation method for calculating Adomian polynomials [J].InternationalJournalofNonlinearSciencesandNumericalSimulation,2007,8(2) ：229-232.

[5] JAFARI H,GHASEMPOUR S,KHALIQUE C M.Comments on He’s homotopy perturbation method for calculating Adomian polynomials [J].InternationalJournalofNonlinearSciencesandNumericalSimulation,2013,14(6)：339-343.

[6] JAFARI H,GHASEMPOUR S,KHALIQUE C M.A comparison between Adomian’s polynomials and He’s polynomials for nonlinear functional equations [J].MathematicalProblemsinEngineering,2013,2013：1-4.

[7] GOLBABAI A,JAVIDI M.A third-order Newton type method for nonlinear equations based on modified homotopy perturbation method [J].AppliedMathematicsandComputation,2007,191(1)：199-205.

[8] WANG F,LI W,ZHANG H Q.A new extended homotopy perturbation method for nonlinear differential equations [J].MathematicalandComputerModelling,2012,55(3/4)：1471-1477.

[9] HE J H.Homotopy perturbation method：A new nonlinear analytical technique [J].AppliedMathematicsandComputation,2003,135(1)：73-79.

[10] BIAZAR J,GHAZVINI H.Convergence of the homotopy perturbation method for partial differential equations [J].NonlinearAnalysis：RealWorldApplications,2009,10(6)：2633-2640.

[11] HE J H.Homotopy perturbation technique [J].ComputerMethodsinAppliedMechanicsandEngineering,1999,178(3/4)：257-262.

[12] HE J H.A coupling method of homotopy technique and perturbation technique for nonlinear problems [J].InternationalJournalofNon-LinearMechanics,2000,35(1) ：37-43.

BasedonHomotopyPerturbationMethodforSolvingNonlinearConversionSumuduFractionalPartialDifferentialEquations

YINWeishi,HANTao

(CollegeofScience,ChangchunUniversityofScienceandTechnology,Changchun130022,China)

In this paper,we use the homotopy perturbation Sumudu transformation method and Sumudu decomposition method to solve the nonlinear fractional differential equations,and the results are compared.The two methods are simple,and the approximate solutions are exactly the same.

fractional partial differential equations;homotopy perturbation Sumudu transform method;Sumudu decomposition method

0427-7104(2017)05-0527-06

2016-09-20

国家自然科学基金(11471067)

尹伟石(1980—)，男，博士研究生，讲师，E-mail：yinweishi@foxmail.com.

O175.14

A