基于BP神经网络的工业园区废弃物物流系统模糊评价研究

何开伦，包秀莉，刘志学

(1.重庆理工大学 管理学院，重庆 400054； 2.华中科技大学 管理学院，武汉 430074)

基于BP神经网络的工业园区废弃物物流系统模糊评价研究

何开伦1,2，包秀莉1，刘志学2

(1.重庆理工大学 管理学院，重庆 400054； 2.华中科技大学 管理学院，武汉 430074)

依据评价指标设计原则，结合系统运作效率与效益、发展生态城市和生态工业园区的要求，从系统投入、系统能力、运作效率、处理效率和环境绩效5个方面提出22个二级指标的园区废弃物物流系统评价指标体系，并利用层次分析法合理确定指标权重，选择12个工业园区为对象进行实例分析，再利用提出的指标体系开展模糊评价，获得模糊评价的输入和评价结果。然后，根据模糊评价过程构建三层结构的BP神经网络，以模糊评价的输入和输出训练BP网络，获得可执行模糊评价的BP网络。实例分析表明：BP网络对各个园区的评价结果与模糊评价结果相同，是评价园区废弃物物流系统绩效便捷、可靠而有效的科学工具。

工业园区；废弃物物流；层次分析法；模糊评价；BP神经网络

综上所述，基于模糊评价法的组合方法具有较高的科学性和可操作性，能解决主客观评价问题，同时可利用专家经验获取必要数据，克服传统评价的弊端。园区废弃物物流系统评价采用的定性和定量指标较多，评价具有模糊性和复杂性，宜采用模糊评价法。上述组合方法研究侧重于评价问题的BP网络实验研究，本研究拟通过建立合理的园区废弃物物流系统评价指标体系，构建基于BP神经网络的园区废弃物物流系统评价系统，为园区管理者提供科学有效的模糊评价工具。

一、工业园区废弃物物流系统评价指标体系设计

园区废弃物物流系统是一个以废弃物处理处置企业为核心，为园区生产企业提供废弃物处理服务的社会性系统，其评价指标及标准的设置较复杂，必须依据指标体系设计原则及要求，设计一套反映不同评价要求的指标体系。

(一)指标体系设计原则和要求

园区废弃物物流系统指标体系设计必须遵循五大原则，包括科学性、系统性、可比性、可操作性和定性定量相结合原则。同时，必须考虑该系统运作效率和效益要求、生态城市和生态工业园区对该系统的要求以及城市、园区和企业可持续发展要求。具体讲，要使指标体系充分体现系统的技术经济特点及可持续发展要求，全面反映系统基础设施、运营能力、服务水平等发展状况及水平，需要积极引入生态城市评价指标包括环境治理和环境质量指标、生态环境健康指标、低碳引领指标[12-14]；引入减量化指标包括万元工业增加值固体废物排放量、万元工业增加值产品包装消耗等，再使用指标包括产品及包装可重复使用的种类占总数的百分比、可重复使用功能研发经费等，再循环指标包括工业固体废物再利用率、产品及包装原级或次级循环率等，来满足发展生态工业园区的要求。

(二)评价指标选取及分析

根据上述指标设计原则和要求，参考有关废弃物物流系统、生态城市、生态工业园区评价指标文献，已颁布的国家生态工业示范园区标准(HJ274—2015)相关指标及要求，按照输入—处理—输出的系统分析思路，从系统投入、系统能力、运作效率、处理效率和环境绩效5个方面归纳和精简可选指标并设计必要的新指标，设计出一个包含两个层次的园区废弃物物流系统绩效评价指标体系。该指标体系包括5类22个二级指标，见表1，具体评价指标分析见表2。

表1中凡企业指标均以所属园区相关企业的平均值衡量。“要求”一栏的数据参考国家生态工业示范园区标准(HJ274—2015)、废弃物管理标准、相关研究成果和专家意见等制定，“要求”为空白的表示该项指标量化数据需要依据园区实际发展水平制定。

表1 工业园区废弃物物流系统绩效评价指标体系

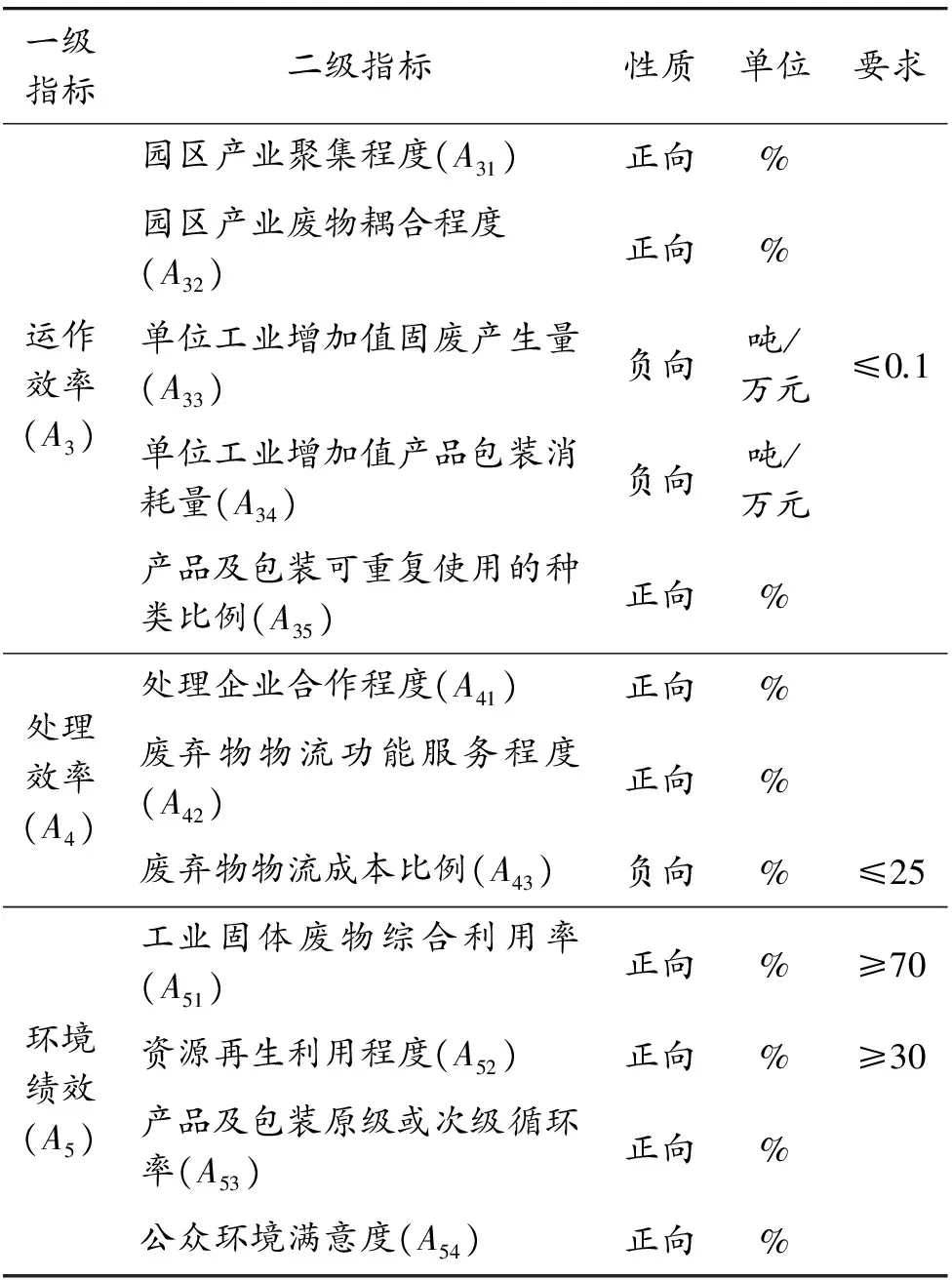
一级指标二级指标性质单位要求运作效率(A3)园区产业聚集程度(A31)正向%园区产业废物耦合程度(A32)正向%单位工业增加值固废产生量(A33)负向吨/万元≤0．1单位工业增加值产品包装消耗量(A34)负向吨/万元产品及包装可重复使用的种类比例(A35)正向%处理效率(A4)处理企业合作程度(A41)正向%废弃物物流功能服务程度(A42)正向%废弃物物流成本比例(A43)负向%≤25环境绩效(A5)工业固体废物综合利用率(A51)正向%≥70资源再生利用程度(A52)正向%≥30产品及包装原级或次级循环率(A53)正向%公众环境满意度(A54)正向%

表2 工业园区废弃物物流系统绩效评价指标分析

续表(表2)

(三)评价指标权重分析

本研究利用层次分析法(Analytic Hierarchy Process，简称AHP)确定指标权重。

1.一级指标层权重分析

根据表1和2将评价问题层次化，得到评价问题的二层结构即一级指标层和二级指标层；利用1-9标度法确定评价尺度，见表3。

表3 标度值及其含义

依据表3赋值Dij，Dij满足条件：Dij>0；Dij=1/Dji(i≠j)；Dii=1 (i,j=1，2，…，n)。

通过访谈形式征询8名专家学者的意见，运用1～9标度法进行两两比较赋值并填表，取赋值作为判断矩阵元素值，得到一级指标层两两比较判断表，见表4。

表4 一级指标层两两比较判断

依据表4可建立一级指标层判断矩阵A：

根据公式CI=(λmax-n)/(n-1)，计算矩阵A的一致性指标CI，其中λmax为矩阵A的最大特征根，n为矩阵A的阶数；在Matlab中计算eig(A)，得到λmax=5.036 1，其对应的特征向量tzxl_A=[0.105 9,0.202 0,0.382 3,0.078 0,0.892 0]，将求得的λmax带入CI计算式可得CI=0.009。根据表5可得到平均随机一致性指标RI的取值，即RI=1.12。

表5 平均随机一致性指标RI

计算随机一致性比率CR=CI/RI=0.008 1<0.1，可见判断矩阵A具有满意的一致性。对特征向量tzxl_A归一化处理后可得到一级指标层各个指标的权重W=[0.063 8, 0.121 7, 0.230 3, 0.047 0, 0.537 2]，即系统投入指标权重W1为0.063 8、系统能力W2为0.121 7、运作效率W3为0.230 3、处理效率W4为0.047 0、环境绩效W5为0.537 2，其中运作效率A3、环境绩效A5权重大，其指标取值对评价结果的影响较大。

2.二级指标权重分析

同样，可得到二级指标层两两比较判断表，建立系统投入层判断矩阵A1、系统能力层判断矩阵A2、运作效率层判断矩阵A3、处理效率层判断矩阵A4和环境绩效层判断矩阵A5，如下：

利用函数eig( )可得到二级指标层各判断矩阵的最大特征根、其对应的特征向量，依据公式计算，可得到相应的随机一致性比率CR，二级指标层权重分析结果如表6所示。

表6 二级指标层权重计算及检验结果

二、基于BP神经网络的评价模型构建及分析

BP神经网络用于评价，相比传统方法具有可操作性强、拟合精度高、科学性强等优点[16]，基于BP神经网络的评价模型具有重要的应用价值。

(一)BP神经网络原理

1.BP神经网络的结构

BP神经网络即误差反向传播神经网络(Back Propagation Neural Networks)，是一种多层前馈神经网络，采用误差反传学习算法，典型的三层BP网络结构如图1所示。

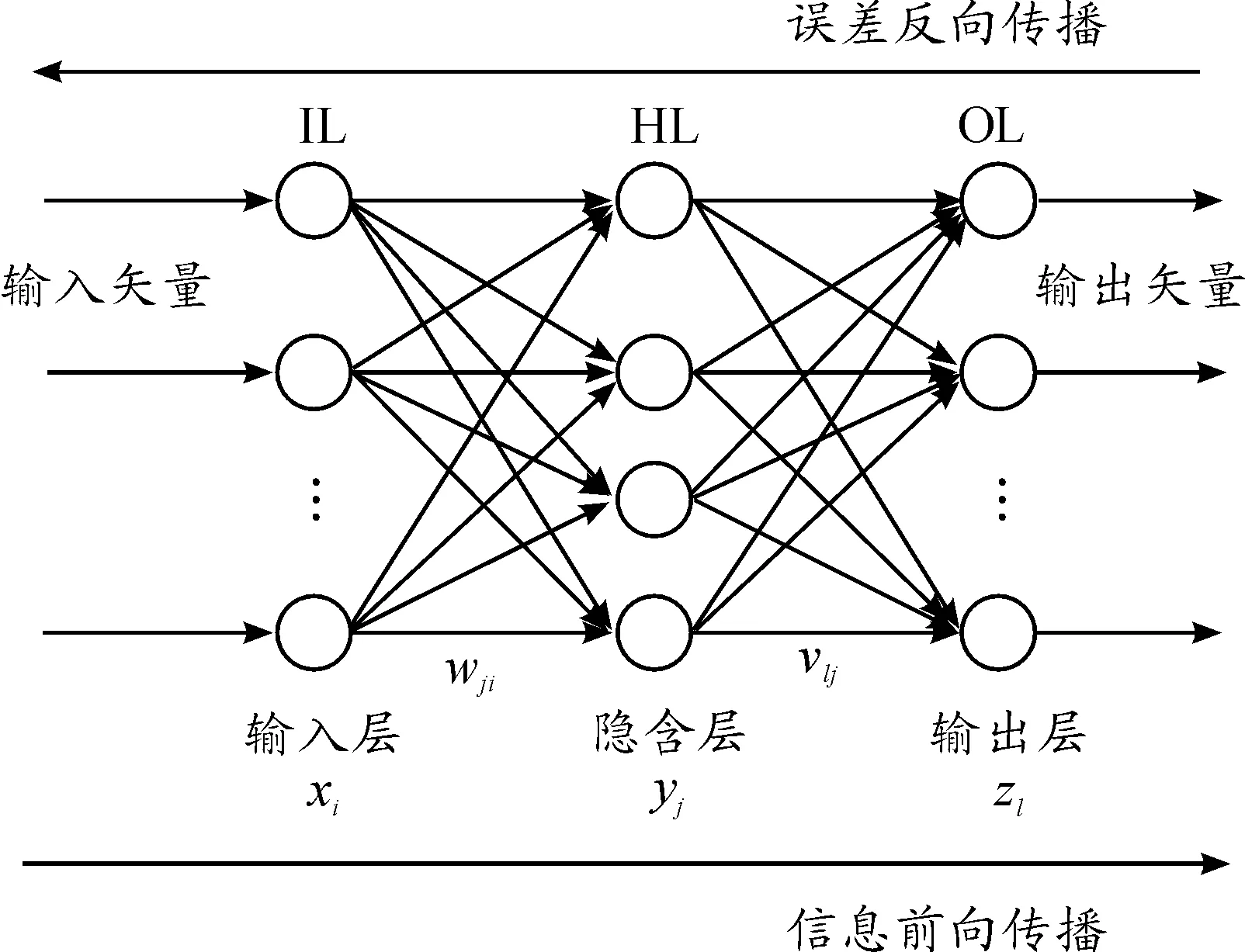
图1 BP网络结构

从图1看出，三层BP网络被分为输入层IL、隐含层HL、输出层OL，同层节点间无关联，不同层神经元间前向连接。

2.BP学习算法

令IL层节点xi到HL层节点yj间的连接权为wji,HL层节点yj到OL层节点zl间的连接权为vlj，θj为HL层节点的阈值，θl为OL层节点的阈值，HL层节点的输出函数为:

(1)

OL层节点的输出函数为:

(2)

其中，f(x)为传递函数，一般为Sigmoid型函数，例如函数f(x)=1/(1+e-x)，采用S型传递函数可以处理和逼近非线性的输入、输出关系。

当输出节点的期望值为tl时，输出节点的误差E为：

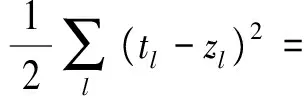
(3)

BP网络训练过程如下:

第一，初始化网络的权值和阈值，即给网络中的wji、vlj、θj、θl等赋初值。一般在区间(-1，1)选取任意数作为BP神经网络的初始连接权值和阈值。

第二，输入学习样本tl，根据输出函数分别计算各层的输出值包括yj、zl。样本信号从输入层经隐含层传向输出层，在输出端产生输出信号。在信号的前向传递过程中，网络的权值是固定不变的，每一层神经元的状态只影响下一层神经元的状态。如果在输出层不能得到期望的输出，则转入误差信号反向传播。

第三，采用梯度下降算法及误差的反向传播修正网络权值和阈值。网络的实际输出与期望输出之间的差值E即为误差信号。误差信号由输出端开始逐层向后传播，网络的权值和阈值由误差反馈进行调节，通过权值的不断修正使网络的实际输出更接近期望输出。隐含层和输出层对网络权值和阈值的调整规则如下:

vlj(k+1)=vlj(k)+Δvlj=vlj(k)+ηδlyj

(4)

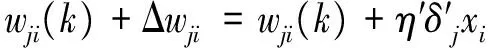
(5)

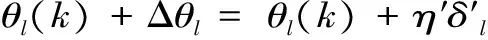
(6)

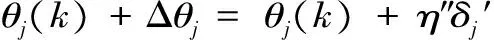
(7)

δl=(tl-zl)·f′(netl)

(8)

(9)

第四，根据训练不断计算误差E，并与预期误差精度进行比较，若实际计算的误差在规定范围内，则学习结束；否则要将学习次数增加一次，并返回到步骤二，按规则调整步长和阈值进一步学习，直到达到规定误差精度或训练次数为止。

(二)评价模型构建

将BP神经网络应用于模糊评价时，可把评价指标体系的实际指标数据作为神经网络的输入向量xi，将相应的模糊评价结果作为神经网络的输出zl，用足够的样本训练网络，使不同组的实测指标得到相应的输出值，将输出值与期望的模糊评价结果值比较，当其误差小于某一设定值时，这时神经网络所持有的权系数值、阈值是网络经过自适应学习所得到的最终权值和阈值。一旦BP神经网络完成训练，就成为有效的模糊评价工具，将实际指标值输入到网络就可以自动对目标做出模糊评价。

BP神经网络构建包括以下3个步骤：第一，确定网络层数和各层神经元数。由于BP神经网络完成m维到n维的映射只需一个三层的BP神经网络，故可选用含有一个隐含层的三层BP神经网络进行设计和训练。输入层节点的数目等于评价指标的数目，输出层节点数即绩效评价结果，其值为1。隐含层节点数可依据经验公式计算确定：

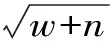
(10)

其中:m为隐含层神经元数，n为输入层神经元数，w为输出层神经元数，a为0～10任意整数。第二，确定传递函数。一般情况下，隐含层采用sigmoid函数，输出层采用线性函数purelin。第三，创建网络，设置训练参数，向网络输入数据，训练网络直到获得符合期望输出的BP网络。

三、实例分析

本实例分析选取重庆的12个工业园区为评价对象，分析评价各个园区2015年的废弃物物流系统绩效。本评价遵循以下步骤：依据提出的指标体系收集数据；应用模糊评价法对园区进行评价，获得模糊评价结果；根据评价需要构建BP神经网络，完成网络训练并进行验证分析。

(一)收集数据

园区废弃物物流系统指标数据来源分为两种：一是调研获取，依据实际数据计算后获得指标值；二是专家打分，对缺乏数据的定量指标和定性指标采取专家调查方法获取数据，即由8个专家对选定园区的指标等级进行投票打分。采取调研方法获取数据的指标有8个，12个工业园区分别用数字1—12表示，8个指标实测值见表7。

目前，工业园区的统计工作起步不久，大多数指标缺乏数据，难以定量计算，需采取专家打分方法获取(14个指标)。进行专家打分时，邀请8位专家对12个工业园区的相关指标逐一进行投票打分，表中单元格数字为5位，从左至右分别表示某园区该指标评价等级为优秀、良好、一般、合格、不合格的专家投票数，每格合计为8票，专家打分的统计结果见表8。

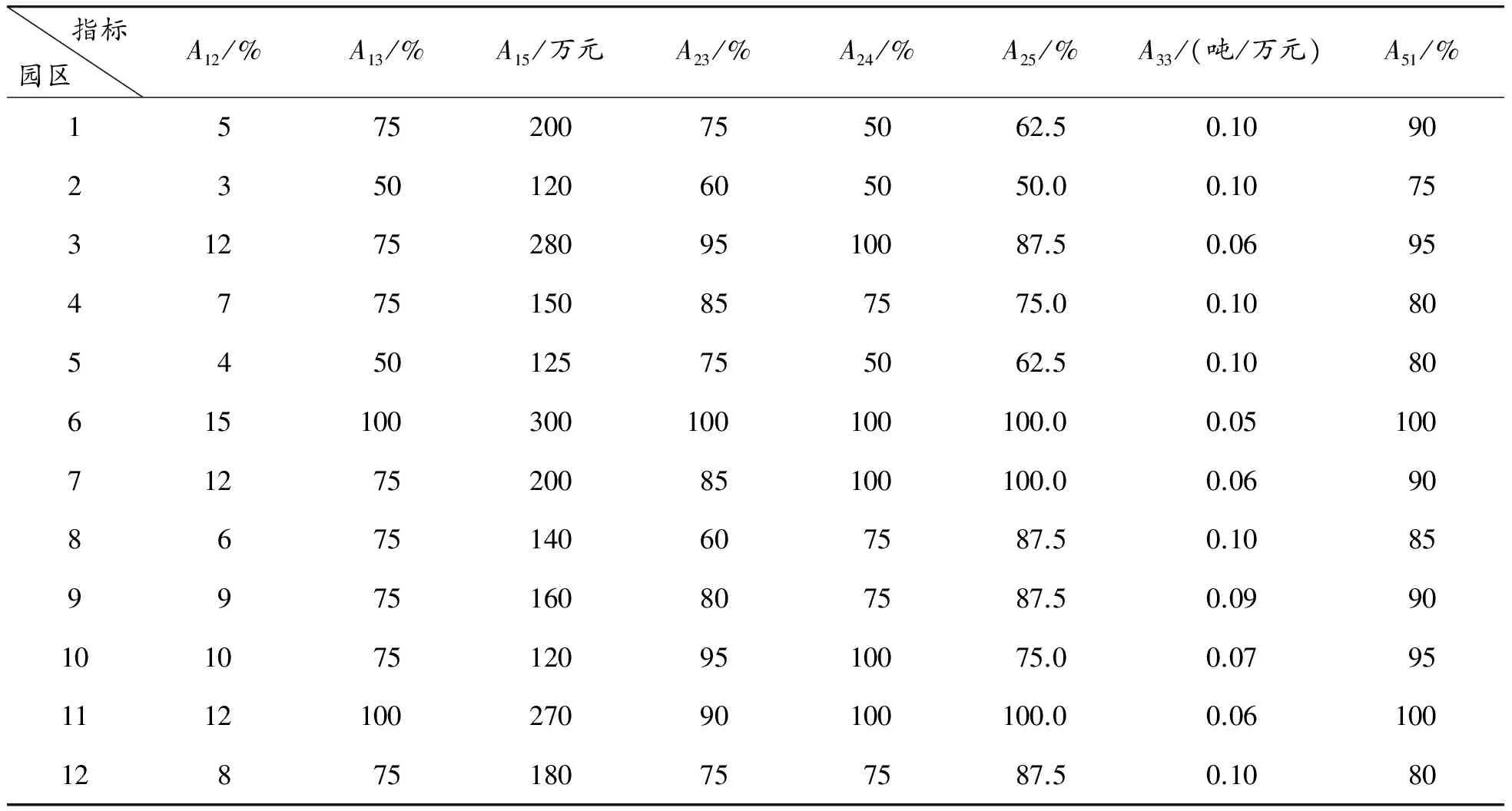
表7 2015年园区废弃物物流系统指标实测值(1)

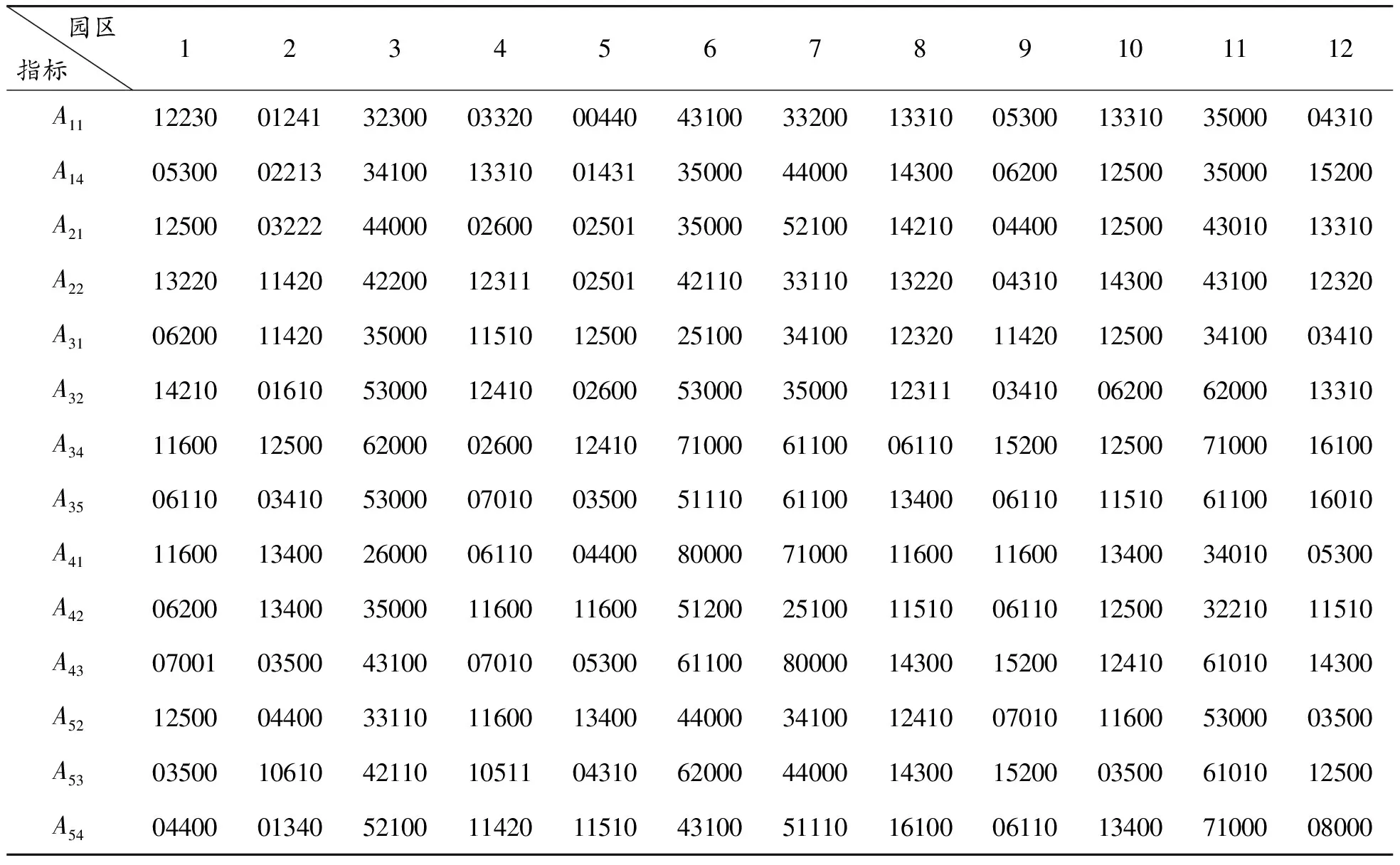
表8 2015年园区废弃物物流系统指标实测值(2)

(二)模糊评价

1.确定因素集、评价集和权重集

根据指标体系确定因素集，主因素集A包括5个因素Ai(i=1,2,3,4,5)对应一级指标层；子因素集Aij(j分别为5,5,5,3,4)包括A1j={A11,A12,A13,A14,A15}，A2j={A21,A22,A23,A24,A25}，A3j={A31,A32,A33,A34,A35}，A4j={A41,A42,A43}，A5j={A51,A52,A53,A54}，对应二级指标层。

评价集采用5个等级，设Vk={v1,v2,v3,v4,v5}={优秀，良好，一般，合格，不合格}。

根据前述分析，主因素权重集W=(Wi)(i=1,2,3,4,5)=[0.063 8,0.121 7,0.230 3,0.047 0,0.537 2]；子因素权重集为Wij(i=1,2,3,4,5)，其中W1j=[0.445 8,0.038 2,0.093 5,0.180 0,0.242 5]，W2j=[0.144 9,0.450 7,0.275 0,0.045 9,0.083 5]，W3j=[0.151 8,0.263 0,0.461 1,0.083 0,0.041 1]，W4j=[0.087 9,0.669 4,0.242 7]，W5j=[0.552 7,0.271 3,0.114 3,0.061 7]。

2.综合评价

(1)指标数据处理

根据指标数据来源，对定性和定量指标采用不同的处理方法，对于表7定量指标，由专家依据相关指标的要求与实际情况确定评价规则进行，每个指标的评价等级是唯一确定的，对判定的等级得8票，其他4个等级得0；对于表8定性指标，依据专家投票数确定等级，根据专家分析，确定表7各项指标评价规则如表9所示。

依据表9，对表7定量指标进行等级评价并给出专家投票数8，将结果与表8合并，得到园区废弃物物流系统指标评价等级投票数，见表10模糊评价需要的指标初值。

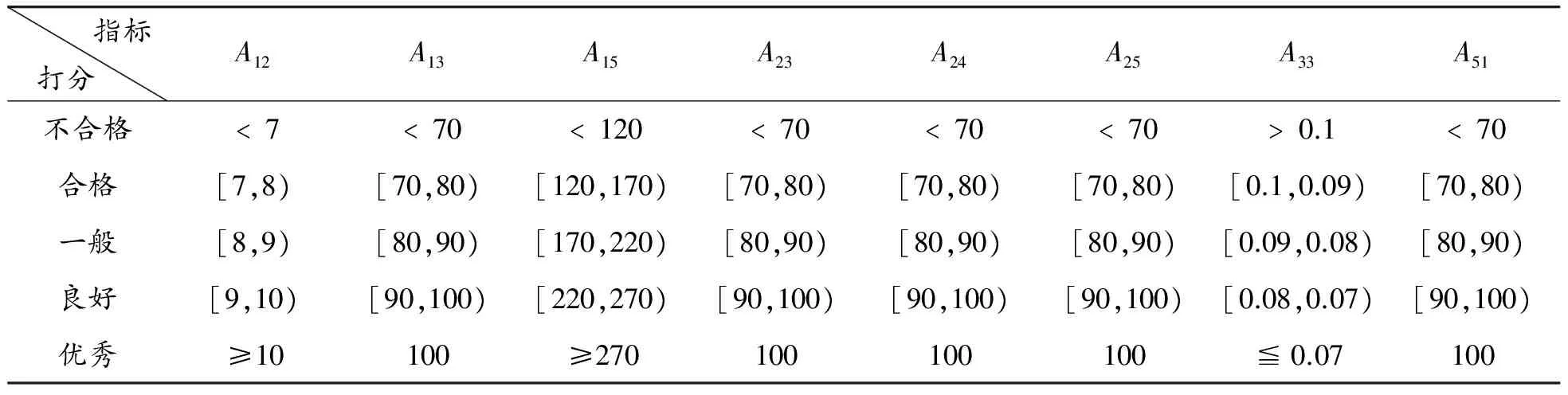
表9 定量指标评价规则

(2)模糊分析

设子因素Aij对评价集Vk的隶属程度为rik，rik=Vik/N,Vik是所有专家中认为Aij隶属于Vk的人数，N=8，分别求出子因素Aij对各个评价等级的隶属程度，得到各子因素的模糊评价矩阵ri(i=1,2,3,4,5)如下：

根据子因素权重集Wij(i=1,2,3,4,5)及ri，利用公式Ri=Wij·ri(i=1,2,3,4,5)，可以得出主因素的模糊评价矩阵R：

根据主因素权重集W及矩阵R，利用公式V=W·R，可得出园区1的评价结果V：

V={0.041 3,0.512 3,0.248 0,0.178 8,0.019 6}

将评价集Vk量化。设5个等级{优秀，良好，一般，合格，不合格}，分别对应[90～100]、[80～90)、[70～80)、[60～70)和[0～60)分，取中间值计算，即分别取95分、85分、75分、65分、30分，则园区1的模糊评价得分为78.279 1，隶属于“一般”。

同理，可对园区2—12进行模糊评价，将评价值汇总于表11中。

表11表明，园区6、11评价值分别为92.203 6、92.125 6，评价结果为优秀；园区3、7、9、10评价结果为良好；园区1、4、5、8、12评价结果为一般，园区2评价结果为合格。该评价结果反映了各个园区废弃物物流发展的实际水平。

(三)构建BP神经网络

1.BP网络结构设计

由上所述，一个三层的BP神经网络可以任意精度完成任意n维到m维的映射，因此本BP评价模型采用三层结构包括输入层、隐含层和输出层。输入层神经元个数为22个，对应22个二级指标；输出层神经元个数为1个，对应模糊评价结果；隐含层神经元个数采用经验公式(10)，确定为10个，BP模型结构如图2所示。

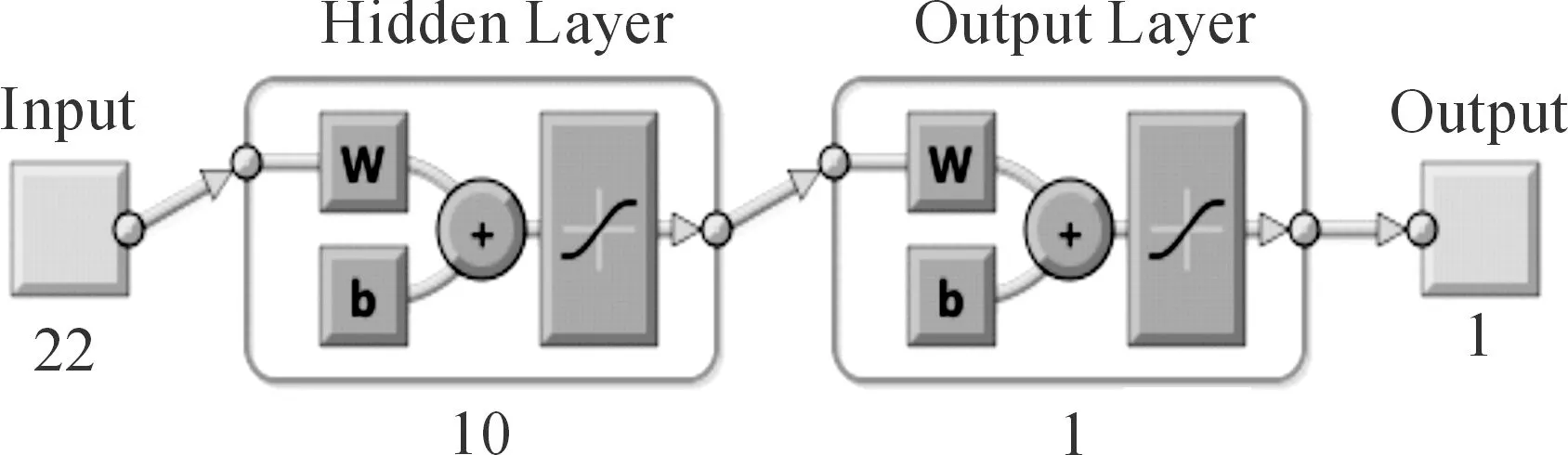
图2 BP神经网络结构

2.创建网络

Matlab软件(2012版)用函数feedforwardnet()建立BP网络，其调用格式为:net = feedforwardnet(hiddenSizes,trainFcn)，其中，net为欲生成的BP网络；hiddensizes指隐含层的神经元个数，默认为10个；trainFCn指BP网络训练函数，默认为Levenberg-Marquardt算法(’trainlm’)。

(1)确定输入输出项

将表10数据分为两部分，选择园区1—10作为训练样本，园区11、12为测试样本。将表10单元格数据逐个除以8，得到对应的指标等级隶属度表。依据该隶属度表、等级量化标准[95,85,75,65,30]，可计算出各个二级指标量化取值，这些值与表10的模糊评价结果(不包括测试样本)共同构成BP神经网络的输入输出项，见表12。

表11 园区废弃物物流系统模糊评价值

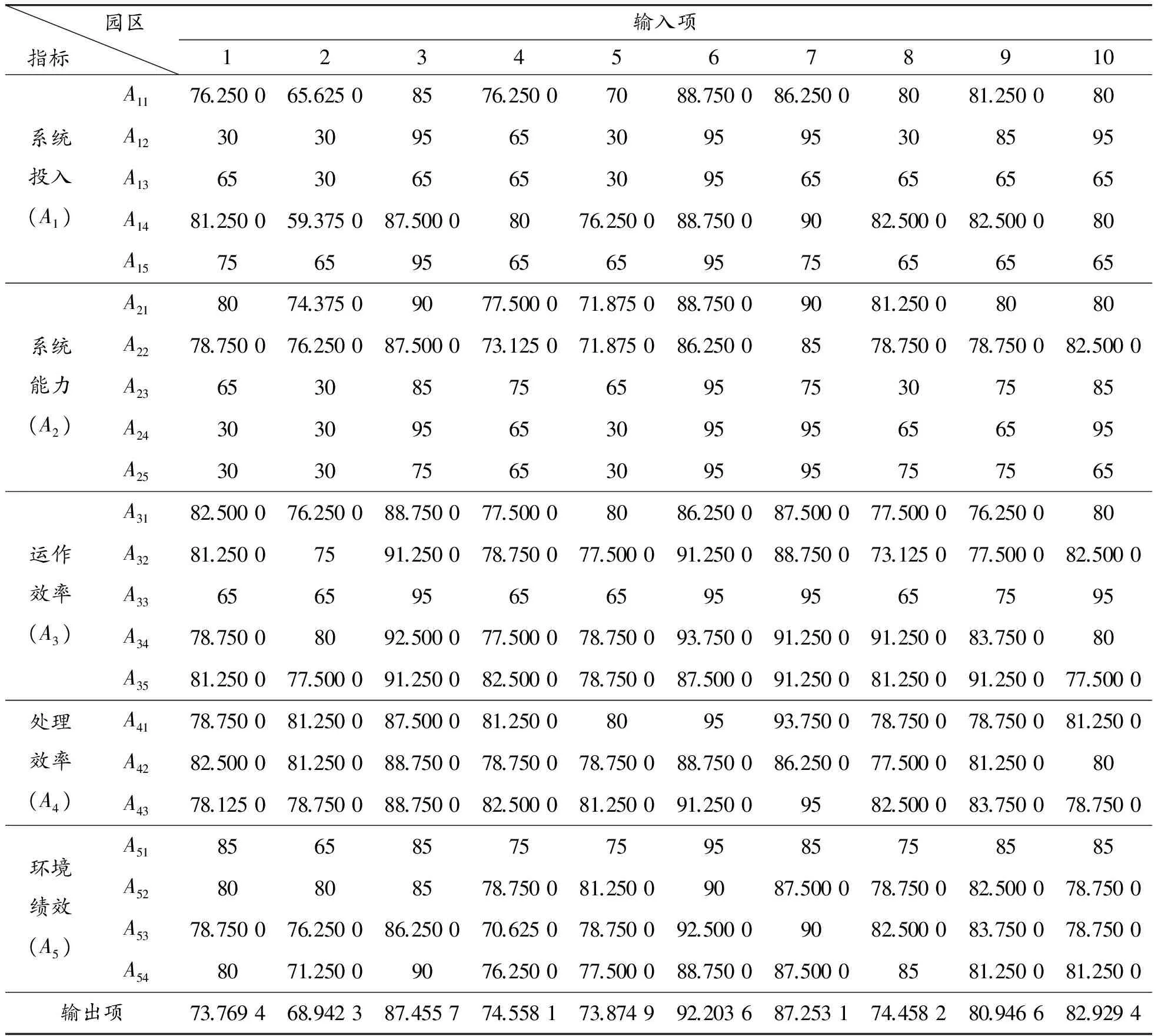
表12 BP神经网络的输入输出项

利用表12数据进行模糊评价，等同于前述模糊评价。利用表12可获得输入项inputs和输出项targets，其中inputs=[22×10]，为22行×10列的矩阵，代表22个二级指标，10个园区；targets=[1×10]=[73.769 4, 68.942 3, 87.455 7, 74.558 1, 73.874 9, 92.203 6, 87.253 1, 74.458 2, 80.946 6, 82.929 4]，为1行×10列的矩阵，代表10个园区的期望输出。

(2)设置网络参数

将矢量inputs 、targets作为欲生成BP网络YQPJ_net的输入输出项。由于带自适应学习率动量梯度下降法适应小样本对象，能避免陷入局部极小问题，所以网络YQPJ_net选用TRRAINGDX作为训练函数。隐层传递函数为log-sigmnid传递函数“logsig”；输出层传递函数为纯线形函数“purelin”；学习函数为带动量的梯度下降学习法“learngdm”；性能函数为均方误差函数“MSE”。数据项和网络参数设置完成后，根据所设计的网络结构，可调用命令YQPJ_net = feedforwardnet(10)，生成评价模型YQPJ_net。

(3)训练网络

YQPJ_net训练参数大部分可取默认值，利用函数net.trainParam设置训练参数见表13。

表13 YQPJ_net训练参数

训练参数设置完成后，利用train()函数对网络进行训练，其调用格式是:[YQPJ_net,tr]=train(YQPJ_net,inputs,targets)，式中inputs，targets分别是输入和输出项；等号左右两侧的YQPJ_net分别代表训练后和训练前的神经网络；tr表示存储网络训练过程中的误差信息和步数信息。

反复训练网络YQPJ_net,通过对10个训练样本的155次迭代，最大失败次数达到10次时结束网络训练，训练精度达到9.06e-7，网络性能见图3,训练状态见图4，输入与期望输出的拟合效果见图5。

图3表明，网络验证性能在144次达到最佳，预测误差为0.010 756；图4表明，YQPJ_net训练结束时(at 155 Epochs)梯度Gradient=0.019 835，验证失败次数Validation Checks=10次，学习率Learning Rate=0.001 919 5；图5表明，训练组、验证组等相关系数R=1，测试组相关系数R=-1、样本输入与输出综合相关系数R=0.998 29，评价模型YQPJ_net取得了较好收敛效果。

图3 YQPJ_net训练精度

图4 YQPJ_net训练状态

完成YQPJ_net训练后，用函数sim()进行仿真测试，其调用格式是:outputs=sim(YQPJ_net,inputs)，outputs代表网络仿真输出。网络YQPJ_net仿真输出园区1—10评价值为[73.789 9，68.924 0，87.451 3，74.518 6，73.963 7，92.090 0，87.391 4，74.478 6，80.937 1，82.953 4]，与实际评价值的误差为[-0.020 476，0.018 339，0.004 380，0.039 489，-0.088 766，0.113 600，-0.138 340，-0.020 357，0.009 471，-0.024 015],可以看出，YQPJ_net输出误差最大仅为-0.138 340，误差可以接受，因此YQPJ_net可有效应用于模糊评价。

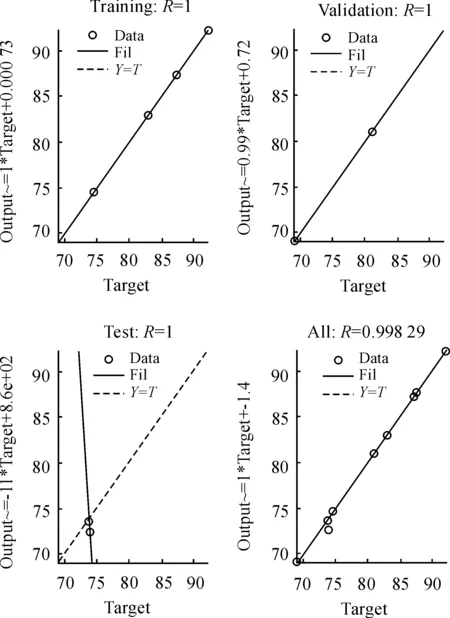
图5 YQPJ_net回归效果

(4)测试分析

将表9测试样本园区11、12数据量化后可得模型的输入项test，test为22行x 2列的矩阵，代表22个二级指标，2个测试园区。调用命令：result=YQPJ_net(test)，运行YQPJ_net可得到园区11、12测试值result=[90.979 4,77.138 7]，与模糊评价值[92.125 6、75.959 6]比较，误差为[1.146 2, -1.179 1]，评价结果相同即园区11为优秀，园区12为一般。可见，YQPJ_net评价结果与模糊评价结果相同，最大误差仅为-1.55%，误差在可接受范围，YQPJ_net评价效率高、误差小，能准确完成模糊评价。

四、结束语

构建园区废弃物物流系统评价体系是消除工业园区废弃物污染、维护城市环境和居民健康的重要手段。本文依据指标设计原则及相关要求，从系统投入、系统能力、运作效率、处理效率和环境绩效5个方面设计出二级园区废弃物物流系统评价指标体系并利用层次分析法确定各层次指标的权重，赋予环境绩效类指标较大权重，以促进工业园区不断提高废弃物综合利用和资源再生利用水平，强化园区产业聚集和废弃物耦合系统建设，实现生态化和可持续发展。实例分析中，将二级指标体系应用于12个园区的模糊评价，获得基于模糊评价法的BP网络。实例分析表明，BP评价模型对各个园区的评价结果与模糊评价结果相同，误差在可接受范围，是评价园区废弃物物流系统绩效便捷而有效的科学工具。BP评价模型能为政府和企业的决策提供相关依据，实用范围广。

为有效构建园区废弃物物流系统评价体系，提出以下政策建议：

第一，构建完善的园区废弃物物流系统。工业园区是区域经济增长的重要部分，同时工业园区也是城市主要的污染源。园区废弃物物流系统是一个为园区生产企业提供废弃物处理服务的社会性系统，其核心为园区废弃物处理处置企业，关键问题是废弃物加工再利用与最终处理。园区废弃物物流系统具有突出的社会效益和环境效益，工业园区要实现可持续发展，一方面需要加大园区废弃物物流的发展力度，消除园区废弃物污染，提高工业园区废弃物的利用技术和处理水平；另一方面政府必须补偿处理处置企业产生的环境效益。

第二，正确评估园区废弃物物流系统评价体系指标权重。园区废弃物物流系统评价涉及诸多因素，评价指标及标准的设置具有复杂性，要保证评价结果的客观、准确，就必须依靠合理的指标体系原则、要求和有效的算法，尽量减少主观因素的影响。为此，应设计一套反映不同评价要求的指标体系，使其评价结果能更好地从园区本身、外部环境等多个方面综合反映园区废弃物物流系统状况，以便更好地评价物流园区废弃物物流系统绩效，促进物流系统的发展和完善，提高物流系统的质量和效益。

第三，完善法律法规和制度建设。依据国家相关法律法规及国家生态工业示范园区标准，制定颁布科学完善的园区废弃物管理条例和实施细则，从环境保护、资格许可、资金投入、废弃物加工再利用与最终处理等方面规范园区废弃物处理和再生资源利用活动，保障园区废弃物物流系统有效规范运行。

[1] 党玮,王海瑞,胡海晨.基于SERVQUAL和LSQ模型的邮政EMS快递服务质量模糊评价研究[J].商业研究,2016(2):170-175.

[2] 宋彩平,金文雯.基于AHP-模糊综合评价法的林产品物流企业综合效益评价研究——以黑龙江省为例[J].林业经济,2016(5):80-83.

[3] 贾亚男,孙鹏.基于BP神经网络的供应商质量评价算法[J].统计与决策,2015(4):172-174.

[4] 孟天醒,文倩,范慧平.基于BP神经网络的河南省可持续发展能力评价[J].湖北农业科学,2016,55(5):1333-1342.

[5] 尹惠斌,游达明.基于BP神经网络的企业突破性创新绩效评价研究[J].软科学,2014,28(5):125-129,144.

[6] 蔡凌曦,范莉莉,鲜阳红.模糊评价方法——BP神经网络在城市节能减排事前评价中的应用[J].新疆社会科学,2014(2):26-32.

[7] 朱庆锋,徐中平,王力.基于模糊综合评价法和BP神经网络法的企业控制活动评价及比较分析[J].管理评论,2013,25(8):113-123.

[8] 李小刚,马友华,张益,等.基于模糊评价与BP神经网络模型的耕地质量评价对比研究——以淮北平原凤台县为例[J].土壤通报,2015,46(4):816-822.

[9] 姜婷.基于神经网络的企业信息能力模糊评价研究——以安徽省制造型企业为例[J].华东经济管理，2015,29(4):177-180.

[10] 邹凯,包明林.基于灰色关联理论和BP神经网络的智慧城市发展潜力评价[J].科技进步与对策,2015,32(17):123-128.

[11] 陈光,李珊珊,董博.基于PCA-BP神经网络的城市轨道交通线网方案评价研究[J].铁道运输与经济,2016,38(2):81-86.

[12] 郭秀锐,杨居荣,毛显强,等.生态城市建设及其指标体系[J].城市发展研究,2001,8(6):54-58

[13] 吴颖婕.中国生态城市评价指标体系研究[J].生态经济,2012(12):51-56.

[14] 付丽娜,贺灵.基于灰色关联分析的低碳生态城市评价研究[J].湘潭大学学报(哲学社会科学版),2013,37(3):31-35.

[15] 刘冠军.工业园区产业集聚评价方法研究——以新疆库车工业园区为例[J].科学学与科学技术管理,2016,37(8):93-101.

[16] 梅强,范茜.基于BP神经网络的高新技术企业自主创新能力评价研究[J].科技管理研究,2011(11):1-4.

ResearchonFuzzyEvaluationofWasteLogisticsSysteminIndustrialParkBasedonBPNeuralNetwork

HE Kailun1,2, BAO Xiuli1, LIU Zhixue2

(1.School of Management, Chongqing University of Technology, Chongqing 400054, China; 2.School of Management, Huazhong University of Science and Technology, Wuhan 430074, China)

Based on the index design principles, combined with the system operation efficiency and benefit requirements, as well as the development requirements of ecological city and ecological industrial park, the evaluation index system of park waste logistics system consisted of 22 indexes with two level is put forward from the five aspects including system input, system capacity, operation efficiency, processing efficiency and environmental performance, meanwhile the index weights are determined reasonably by using the method of analytic hierarchy process. The 12 industrial parks are selected as the object of case analysis to be evaluated by the fuzzy evaluation method and the proposed index system, and the inputs and evaluation results of the fuzzy evaluation are obtained. Then according to the fuzzy evaluation process, the three layered BP neural network is constructed, trained by the input and outputs of the fuzzy evaluation, and the BP network is obtained to perform fuzzy evaluation. The example analysis shows that the evaluation result of the BP network is the same as the fuzzy evaluation, which is a convenient, reliable and effective scientific tool to evaluate the performance of waste logistics system.

industrial park; waste logistics; Analytic Hierarchy Process (AHP); fuzzy evaluation; BP neural network

2017-03-15

国家自然科学基金项目“物流服务模式对供应链绩效的影响研究”(71072034)

何开伦(1965—)，男，重庆人，重庆理工大学管理学院教授，华中科技大学管理学院博士研究生，研究方向：物流与供应链管理； 包秀莉(1992—)，女，四川广安人，硕士研究生，研究方向：现代管理理论及应用；刘志学(1964—)，男，湖北武汉人，教授，博士生导师，研究方向：物流与供应链管理。

何开伦，包秀莉，刘志学.基于BP神经网络的工业园区废弃物物流系统模糊评价研究[J].重庆理工大学学报(社会科学)，2017(10):37-50.

formatHE Kailun, BAO Xiuli, LIU Zhixue.Researchon Fuzzy Evaluation of Waste Logistics System in Industrial Park Based on BP Neural Network[J].Journal of Chongqing University of Technology(Social Science)，2017(10):37-50.

10.3969/j.issn.1674-8425(s).2017.10.006

F205

A

1674-8425(2017)10-0037-14

(责任编辑张佑法)