双层斜拉桥车辆碰撞动力响应分析

沈正峰，康斌锴，戈海玉

(1.皖西学院 建筑与土木工程学院，安徽 六安 237012；2．长安大学 公路学院，陕西 西安 710064)

双层斜拉桥车辆碰撞动力响应分析

沈正峰1,2，康斌锴2，戈海玉1

(1.皖西学院 建筑与土木工程学院，安徽 六安 237012；2．长安大学 公路学院，陕西 西安 710064)

通过已有文献进行箱梁截面设计，并用Midas计算截面特性赋予 Ansys单元，建立双层箱梁斜拉桥有限元模型。根据现有车-桥碰撞力计算方法，分别施加不同形式的车辆碰撞力，分析斜拉桥在不同荷载工况下的位移、速度、加速度特性，为此新型桥梁结构防撞设计提供参考。

双层斜拉桥；碰撞力；动力分析；阻尼比；位移

随着桥梁设计理论的完善以及施工技术的发展，双层桥因结构新颖、技术先进、经济美观被广泛使用。2005年1月9日，澳门西湾大桥建成通车，它是世界首座预应力混凝土双层箱梁斜拉桥，其连接澳门半岛与氹仔岛，桥梁总长1 825 m，上层通行六线汽车、下层通行两线轻轨和两线汽车，下层车道能满足台风期间交通运输要求，大桥采用了无横隔板箱形截面梁设计，结构高度最大值为6.13 m，箱梁内配备有完整的排风，照明，防火等设备施设[1]。该桥在设计之初进行了完整的抗风、抗震等技术研究，但是对于箱内防撞设计研究资料不多。由于箱梁内部是一个封闭的行车环境，如果发生车辆碰撞，会造成极大的经济、人员损失。本文通过Ansys建立双层斜拉桥全桥模型，根据现有碰撞力计算方法，对结构施加碰撞力，分析结构动力特性，为此类桥梁设计提供参考。

1 模型建立

根据斜拉桥的结构形式不同，采用的有限元模型也不同，由于梁单元相比实体、壳单元更加简便，其在斜拉桥建模中被广泛使用。斜拉桥梁单元模型主要有以下种：单主梁模型、双主梁模型、三主梁模型等[2]。单主梁模型适用于闭口箱型截面，能够正确的计算主梁的竖弯刚度和质量，建模方便快捷，是在结构动力特性分析中广泛使用的一种模型。该方法将主梁简化为一根纵梁，竖向刚度、扭转刚度、弯曲刚度及剪切刚度均集中在主梁上，通过定义集中质量矩考虑结构扭转，人行道板、风嘴、栏杆以及二期铺装等附属结构用集中质量单元来模拟。双主梁模型将主梁竖向刚度平均分配给二边主梁，其近似考虑了主梁的约束扭转效应。1992年，项海帆、朱乐东提出三主梁模型，其考虑了主梁的翘曲刚度影响，适用于自由扭转刚度小的主梁截面，如叠合梁截面。由于本研究采用箱梁截面，其抗扭刚度大，故采用单主梁模型。根据现有规范和研究资料，进行实用双层斜拉桥设计，箱梁截面采用文献[3]截面，用Midas计算截面特性，赋予Ansys梁单元实常数。在Ansys里分别使用Beam4、Beam44单元建立主梁、桥塔结构；拉锁采用Link10单元模拟；二期铺装、栏杆、横隔梁质量采用质量单元Mass21单元模拟，施加到主梁单元节点上，Mass21单元需要定义转动惯量，计算方法如下公式所示。

1.1 桥面铺装层

由于铺装层厚度比桥宽小很多，因而可以忽略铺装层截面竖向抗弯惯矩，近似等效计算公式如下：

其中ρ是铺装层材料密度，h和b分别为铺装层厚度和宽度，A为铺装层截面面积，d为铺装层质心距主梁质心距离。

1.2 横隔梁

一般横隔梁数目多，截面含有大量加劲肋，且在辅助墩等部位截面较大，假设其在纵桥向均匀分布，在辅助墩等横隔梁截面较大的部位，按照实际情况放大平均值，计算方法如下：

其中m表示横隔梁平均质量，n表示横隔梁总数，Ip表示横隔梁极惯性矩，A为标准横隔梁面积，l表示桥长。

1.3 护栏及其他集中质量构件

假设护栏质量沿桥长均匀分布，按照转动惯量的定义，计算方法如下：

其中mi表示护栏沿桥长平均质量或集中质量构件，ri表示距主梁质心的距离。

主梁和拉锁通过横向刚臂连接，耦合塔梁单元自由度，有限元模型图1所示。在进行瞬时动力分析之前，先进行结构的模态分析，得出结构模态参数，根据文献[4](P4-8)施加结构阻尼，由于钢筋混凝土结构阻尼比一般为3%～8%,本研究采用0.05，计算结构Rayleigh阻尼，α=1.83E-02,β=1.15。

图1 斜拉桥模型

2 碰撞力分析

现阶段，车撞桥的碰撞力获取主要通过理论推导、有限元仿真、实车试验等方式。文献[5]通过车辆运动学及能量原理，分析了碰撞力的变化规律，得出1/4余弦式冲击荷载下混凝土护栏承载能力设计方法。文献[6]、[7](P109-141)通过理论分析，由碰撞过程中冲量相等原理，选择便于工程运用的半波正弦简化计算碰撞力方法。文献[8]编制了计算冲击力程序,对比规范结果进行研究，并参考国内外的实车试验结果，利用Matlab程序拟合碰撞力计算公式。文献[9]通过非线性有限元LS-DYNA，改变车辆的质量、碰撞角度、碰撞速度，拟合出碰撞力计算公式。本文选择碰撞角度为20°，碰撞速度为80 km/h，车辆质量为1.238 9 t，碰撞时间为0.125 s,取文献[7](P109-141)、[8]半波正弦碰撞力曲线和文献[9]有限元计算碰撞力曲线，分析横向施加到桥梁跨中处结构的动力特性。半波正弦时程曲线和非线性有限元时程曲线计算的碰撞力峰值分别达到119.2 KN和206 KN,具体如下图所示。

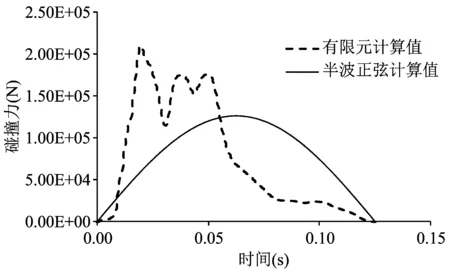
图2 碰撞力时程曲线

3 计算结果分析

选择ANSYS瞬态分析方法，通过定义荷载-时间表参数施加渐变的碰撞力荷载曲线，提取跨中节点碰撞横桥向位移，速度、加速度，对比求解结果如下所示：

图3 跨中节点Z方向位移时程曲线

图4 跨中节点Z方向速度时程曲线

图3可以得出在整个碰撞过程中节点位移不断增加，增加速度先快后慢，这和荷载曲线吻合；碰撞结束后，结构虽然没有收到外荷载作用，但是速度仍然为正，位移不断加大，在1.672 5 s时刻,节点位移达到峰值，有限元荷载工况峰值比正弦半波荷载工况方式大，二者分别为2.74E-4 m和2.47E-4 m，因而桥梁在小型汽车的冲击下，横桥向位移非常小。从图4得出，节点速度在碰撞结束立即下降，并趋向负值，最后在阻尼的作用下趋于0，有限元计算荷载工况和等效正弦加载工况相差很小。分析图5知，节点受到冲击力作用，加速度瞬间达到最大，并在碰撞过程中就下降，整个桥梁加速度值很小，随着碰撞结束，加速度立即消失，有限元荷载工况得到的峰值远远大于等效正弦工况，但是等效半波正弦产生的加速度峰值减少较缓，这和二者的荷载时程曲线特征有关。

图5 跨中节点Z方向加速度时程曲线

4 结论

本文通过建立斜拉桥有限元模型，通过已有的车桥碰撞资料，将冲击力施加到桥梁跨中，初步研究在车辆碰撞力作用下，整个桥梁的动力特性，得出以下结论：

(1)在小型汽车的作用下，根据非线性有限元计算的瞬时碰撞力峰值达到206 KN，等效正弦碰撞力119 KN，但是二者在荷载方向上引起的结构动力响应非常小，并且在阻尼的影响下很快趋于平衡状态，其对整个桥梁的影响不大。

(2)二种不同的碰撞力时程曲线引起的结构动力响应峰值相差很小，在结构设计中采用半波等效荷载法代替非线性有限元乃至实车试验能够节约时间和资源。

(3)从结果分析可以得出，对于双层斜拉桥下层车道的防撞设计主要是做好局部构件的耐瞬时冲击，防止材料在瞬时冲击力作用下失效。

[1]廖慕捷，张强.澳门西湾大桥引桥上部结构设计[J].铁道标准设计，2005(6)：68-70.

[2]方志，张国刚，唐盛华，等．混凝土斜拉桥动力有限元建模与模型修正[J]．中国公路学报，2013，26(3)：77-85.

[3]姚良云，陈燊.双层连续箱梁桥开孔箱内壁车辆碰撞仿真研究[J].福州大学学报，2012，40(5)：640-643.

[4]王新敏.ANSYS结构动力分析与应用[M].北京：人民交通出版社，2014.

[5]卫军，张萌，杨曼娟，等.混凝土结构道路护栏设计计算方法[J].浙江大学学报，2014，48(2)：249-253.

[6]王君杰，卜令涛，孟德巍.船桥碰撞简化动力分析方法：简化动力模型[J].计算机辅助工程，2011，20(1)：70-75.

[7]陆新征，何水涛，黄盛楠.超高车辆撞击桥梁上部结构研究——破坏机理、设计方法和防护对策[M].北京：中国建筑工业出版社，2011.

[8]石红星，白书锋，吕伟民.车与混凝土护栏碰撞的冲击力简化模型[J].公路交通科技，2002，19(2)：114-116.

[9]沈正峰，郑净，涂劲松，等.双层交通矮塔斜拉桥箱内车辆碰撞力比较研究[J].井冈山大学学报(自然科学版)，2016，37(2)：66-101.

DoubleCable-stayedBridgeVehicleCollisionDynamicAnalysis

SHEN Zhengfeng1,2, KANG Binkai2, GE Haiyu1

(1.DepartmentofArchitectureAndCivilEngineering,WestAnhuiuniversity,Lu’an237012,China;2.SchoolofHighway,Chang’anUniversity,Xi’an710064,China)

Through the existing literature for box girder section design, calculate the cross-section characteristics of the box girder by Midas and establish the finite element model of double-decked girder cable-stayed bridge by Ansys. According to the calculation method of existing vehicle-bridge collision force, applying different forms of vehicle collision force and analysis the displacement, velocity and acceleration characteristics of the cable-stayed bridge. It can provide the reference for this new type of bridge structure anti-collision design.

double cable-stayed bridge; collision force; dynamic analysis; damping ratio; displacement

U448.27

A

1009-9735(2017)05-0141-03

2017-04-11

皖西学院校级项目(WXZR201624)。

沈正峰(1987-)，男，安徽舒城人，博士研究生，讲师，研究方向：结构振动控制。