基于直接磁链控制的并联逆变器下垂控制策略研究

王艾萌， 张 佳

(华北电力大学 电气与电子工程学院，河北 保定 071003)

基于直接磁链控制的并联逆变器下垂控制策略研究

王艾萌， 张 佳

(华北电力大学 电气与电子工程学院，河北 保定 071003)

在传统的下垂控制中，通过电压-频率下垂方法实现功率的分配，需要用到复杂的多重环路控制和Park变换，功率分配时频率偏差较大。针对这些问题，采用了基于虚拟磁链的下垂控制方法，通过磁链-相角下垂实现功率的调节。之后，设计了一种改进的直接磁链控制器，基于直接磁链控制(DFC)原理实现了磁链相角和幅值的控制，取代了传统下垂控制中的多重反馈环路和PI调节器，具有控制简单，动态响应速度快，磁链脉动小等优点。最后，利用MATLAB/Simulink软件搭建了具有两个并联逆变器的简化微网模型用以验证设计的控制策略的有效性。仿真结果表明，所设计的控制策略具有良好的动态响应和静态稳定性，并且与传统的下垂控制方法相比，具有更小的频率偏差。

微电网； 下垂控制； 虚拟磁链； 直接磁链控制

0 引 言

随着化石能源的枯竭和环境的恶化，寻求清洁能源对于可持续发展和环境保护尤为重要。近年来，微电网受到了广泛的关注。微电网是指一个小型的发配电系统，采用现代电力电子技术，将分布式电源、储能设备、负荷等进行组合，直接连接在用户端。采用微电网供电方式，可以充分利用可再生能源，成为缓解能源问题的新途径[1]。

优良的控制系统是实现微电网灵活运行和提高供电质量的保证，也是微网技术研究的主要方面。微网的控制方式主要分为两种：主从控制和对等控制。前者利用全局信息实现控制，对通信的要求较高。考虑到微源的分散性，全局控制存在局限性；后者利用本地信息实现控制，克服了微源的地理位置带来的局限性，有利于实现“即插即用”，受到了广泛关注[2-4]。其中，下垂控制是微网控制中最常用到的控制策略。下垂控制利用有功-频率，无功-电压下垂特性实现微网的控制，具有相对高的灵活性。

然而，传统的下垂控制策略存在一些问题。一方面，在传统的“功率-电压-电流”三环控制策略中，需要复杂的多重反馈环路控制，Park变换和PI调节[5]。令一方面，在功率分配时，频率较大程度的偏离额定值，损害电能质量，不满足一些重要的电力设备的运行要求。

近年来，各种改善传统下垂控制性能的方案相继被提出。文献[6]中提出了根据功率变化实时调整下垂系数的自适应微电网控制策略。在频率和电压幅值的闭环控制中不断改变下垂系数，从而将母线电压稳定在一定的水平，有效地减小了逆变器输出功率变化对电压和频率的影响。文献[7]提出了在下垂控制器中加入微分-积分项，并且通过建立并联逆变器的小信号模型验证了加入微分-积分项可以提高系统的暂态响应。文献[8]提出在阻性线路中采用无功-相角下垂控制策略，与传统的无功-频率下垂控制策略相比，前者可以降低微网孤岛运行时的频率偏差。文献[9]分析了无功功率分配不均的原因，通过估计阻抗电压降提出了准确的无功功率分配算法。分析了线路特性对下垂控制的影响，引入了虚拟阻抗解决阻感线路带来的功率耦合问题，从而把传统的下垂控制策略应用到中低压网络。然而，上述方案都是基于电压下垂的方法提出的，因此传统下垂控制的问题仍然存在。

针对传统下垂控制方法的局限性，本文研究了一种基于DFC的磁链下垂控制策略。首先，建立了微网中功率与虚拟磁链的数学模型，由此得到了基于虚拟磁链的下垂控制方法。然后，通过更紧密的空间划分，设计了一种改进的直接磁链控制器，取代了传统下垂控制中的多重反馈环路和PI调节器，减小了磁链的脉动性。最后，分析了基于虚拟磁链的微网总体控制策略，并通过仿真验证了本文所提控制策略的有效性。

1 下垂控制方法

1.1传统的下垂控制方法

图1为微网中的逆变器等效模型。其中，V,E,I分别代表微源输出侧电压,负载侧电压，线路电流。P,Q为微源向负载提供的有功功率和无功功率。Z,δ分别表示线路阻抗和相角，满足：Z=R+jwL=R+jX=|Z|∠φZ,δ=φV-φE。

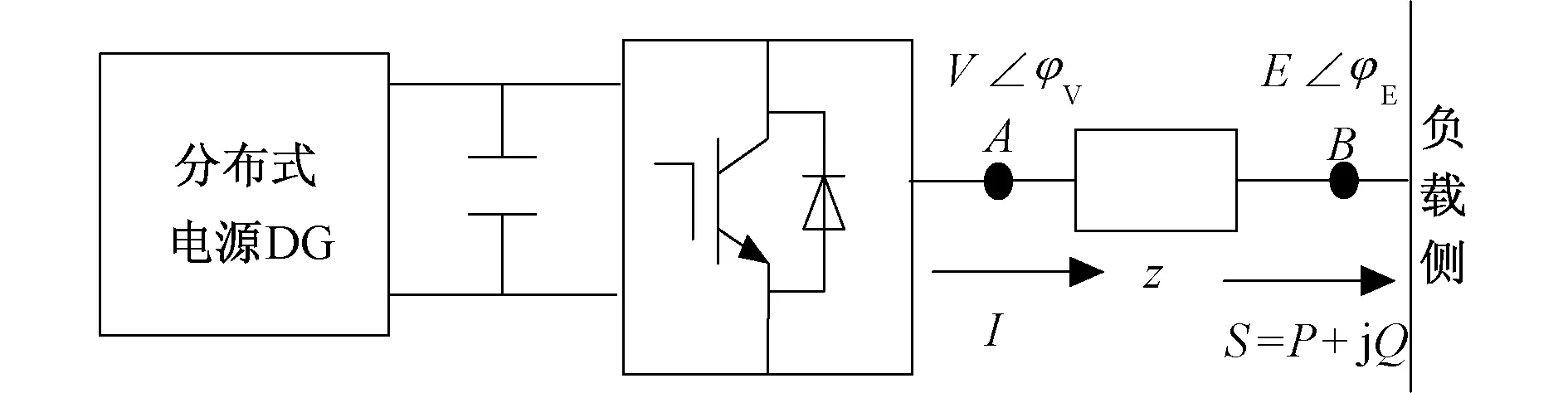
图1 微网中逆变器的等效电路Fig.1 Equivalent circuit of a inverter in microgrid

从图1中，可得微源向负载注入的功率为[5]

(1)

(2)

因为线路通常以感性为主，即：∠φz≈90°，式(1)，(2)变为

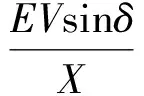
(3)

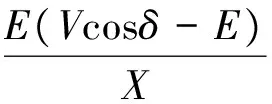
(4)

考虑到相角δ一般很小，故sinδ≈δ,cosδ≈1。

从而得到：

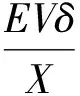
(5)

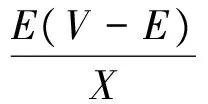
(6)

式(5)、(6)表明有功功率与相位成比例，无功功率与电压幅值成比例，从而得到传统的下垂控制公式：

w=wn-m(Pn-P)

(7)

V=Vn-n(Qn-Q)

(8)

式中：w,wn分别表示微网中的频率及其额定值，Pn,Qn表示额定的有功与无功功率，m,n表示有功-频率，无功-电压的下垂系数；

传统下垂控制的总控制结构如图2所示。包括功率计算模块，下垂控制器，电压电流双环控制

模块，SPWM调制模块等。在传统下垂控制中，为了把测量量从三相静止坐标系转换到两相旋转坐标系，需要复杂的坐标变换；为了确定电压外环和电流内环的控制参数，需要复杂的参数调试；最主要的，在传统下垂控制中对频率的直接控制会造成频率偏差较大，损害电压质量。

图2 传统的多环反馈下垂控制结构Fig.2 Control structure of traditional droop method with multiple feedback loops

1.2基于虚拟磁链的下垂控制方法

为了避免传统下垂控制的复杂性和频率偏差较大的问题，从虚拟磁链的角度重新设计了下垂控制方法。

从图1中，可得

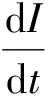
(9)

S=EI*

(10)

考虑到电压的积分为磁链，即

(11)

(12)

从(11)式中，可以得到微源输出磁链与电压的幅值和相角关系：

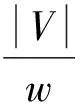
(13)

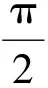
(14)

负载侧电压与磁链的幅值和相角关系与(13)、(14)式类似。

线路以感性为主时，式(9)中的电阻项可以忽略不计。此时，对式(9)两端求积分，可得

(15)

将(15)式代入(10)式，得到：

(16)

进一步展开，可得

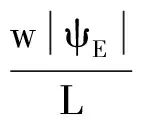
(17)

因为相角满足：δ=δV-δE=δfV-δfE，则从(17)式中得到

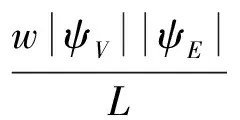
(18)

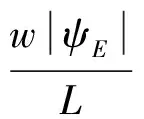
(19)

考虑到相角δ一般很小，最终可得

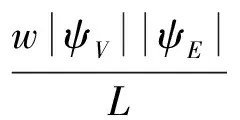
(20)

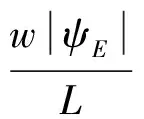
(21)

从式(20)，(21)中可知，有功功率与相角成比例，无功功率与微源输出侧的磁链幅值成比例。从而得到基于虚拟磁链的下垂控制公式：

δ=δn-mf(Pn-P)

(22)

|ψV|=|ψV|n-nf(Qn-Q)

(23)

式中：δn,|ψV|n表示额定相角和磁链幅值，mf,nf表示有功-相角，无功-磁链的下垂系数。

2 改进的直接磁链控制器设计

从(22)、(23)式可知，在磁链下垂方法中只需控制磁链幅值|ψV|和相角δ两个变量。为了避免复杂的多重反馈环路控制，设计了直接磁链控制器，通过两个滞环比较器直接控制磁链幅值|ψV|和相角δ,具有控制简单、动态响应速度快，对参数鲁棒性强的优点[10]。

DFC的原理如图3所示。将磁链幅值和相角信息送入两个滞环比较器，根据滞环比较器输出的偏差符号，再结合逆变器磁链矢量的当前位置，通过查询矢量选择表选择合适的开关状态，从而将磁链幅值和相角控制在参考值附近。

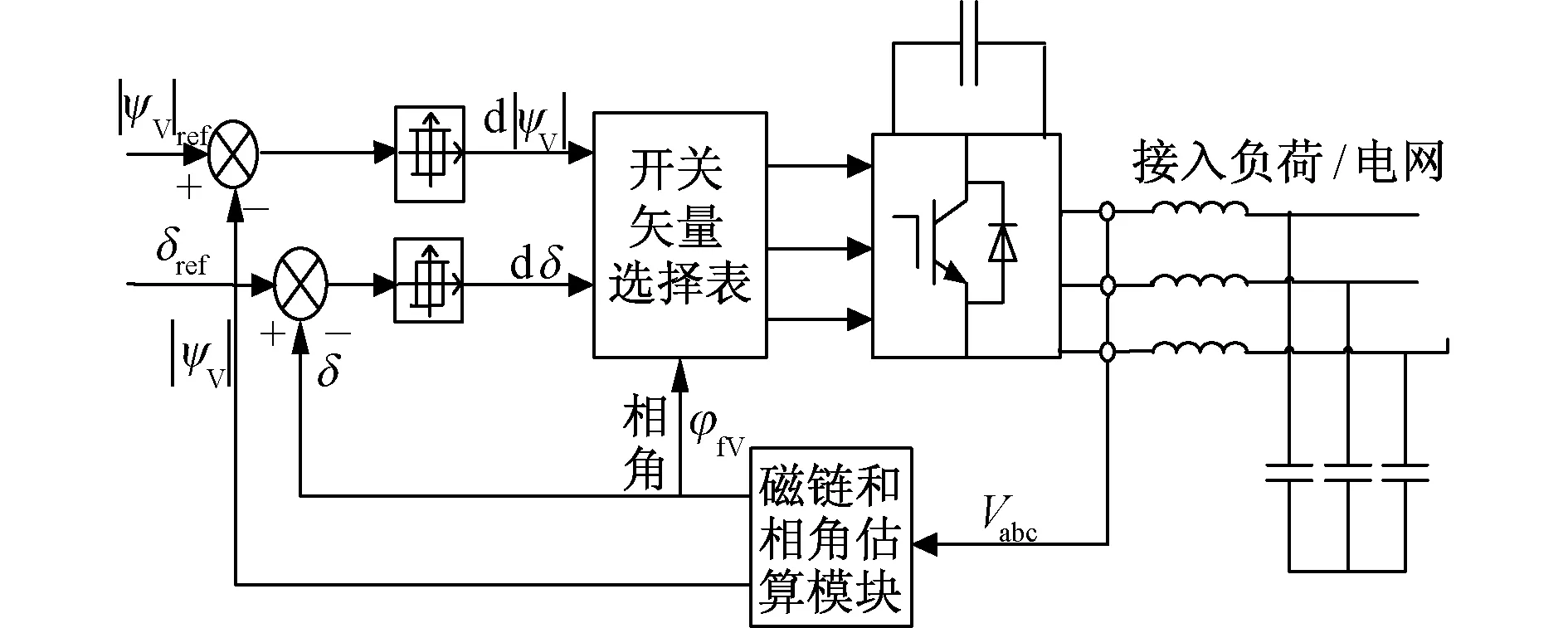
图3 DFC控制原理图Fig.3 Control diagram of DFC

在基于磁链的下垂控制中，为了避免复杂的坐标变换，将变量转换到两相静止坐标系，即α-β坐标系中讨论。

在DFC中，磁链幅值|ψV|和相角φfV的计算如式(24)～(27)，其偏差信号d|ψV|和dδ的取值情况如式(28)、(29)所示。

(24)

(25)

(26)

(27)

(28)

(29)

传统的坐标平面划分如图4所示。将α轴作为S1扇区的中心，按逆时针方向将平面均分为6个扇区(S1-S6)，每个扇区60°。图中有8种不同的开关状态，对应6个工作电压矢量(V1-V6)和两个零开关矢量(V0和V7)。所有的工作电压矢量都使得相角增加，为了减小相角，需要选择零矢量[11]。

图4 平面的6扇区划分Fig.4 6 sectors division of α-β plane

表1为传统平面划分时的开关矢量选择表。表中，d|ψV|=1和d|ψV|=0分别表示需要增加磁链和减小磁链；dδ=1和dδ=0分别表示需要增加相角和减小相角。当逆变器输出磁链矢量位于S1扇区时，若|ψV|ref<|ψV|,δref<δ，则选择V2矢量来增加磁链的幅值和相角。

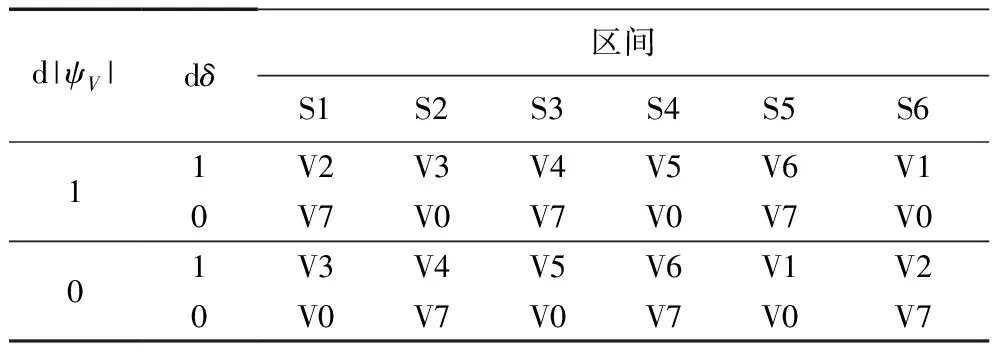
表1 6扇区电压矢量选择表

考虑到传统6扇区划分时，磁链的轨迹脉动较大影响电压静态稳定性的问题，本文采用了12扇区划分方法，即将6扇区包围的空间再细分为两部分，从而划分出12个扇区，每个扇区30°。通过更为紧密的扇区划分，可以提高磁链控制的准确性，减小磁链脉振。具体划分情况如图5所示。表2为12扇区划分时的开关矢量选择表。与传统的6扇区控制原理相同，利用图中8个电压矢量可以实现磁链幅值和相角的控制。

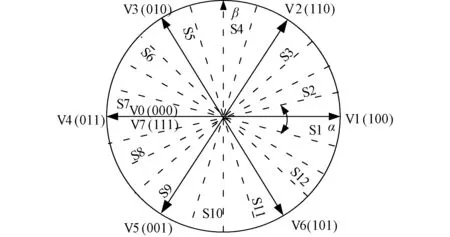
图5 平面的12扇区划分Fig.5 12 sectors division of α-β plane

区间d|ψV|10dδ1010S1V2V7V3V0S2V2V7V4V7S3V3V0V4V7S4V3V0V5V0S5V4V7V5V0S6V4V7V6V7S7V5V0V6V7S8V5V0V1V0S9V6V7V1V0S10V6V7V2V7S11V1V0V2V7S12V1V0V3V0

3 微网控制总体结构

图6为基于虚拟磁链的微网总体控制结构，包括磁链下垂控制器和直接磁链控制器两部分。在微网下垂控制中，系统控制的核心作用是支撑微源输出电压和频率的稳定[12]。在本文所提的控制策略中，通过控制磁链幅值和相角即可实现建立稳定电压的目的。

图6 基于虚拟磁链的微网控制结构Fig.6 Control structure of microgrid based on virtual flux

在磁链下垂控制器中，瞬时有功功率p和无功功率q的计算如式(30)，(31)，将其通过低通滤波器得到平均有功功率P和无功功率Q。功率经过磁链下垂模块得到磁链和相角的参考值，然后与磁链和相角估计模块得到的实际值进行比较，将差值信号送入直接磁链控制模块，从而实现对磁链和相角的跟踪控制。

(30)

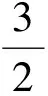
(31)

为了向孤岛运行的微电网提供交流参考电压，可以通过对ψV和ψE的控制间接实现对负载侧电压E的控制。在磁链下垂控制器中，通过磁链幅值实现电压幅值的调节,如式(32)：

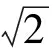
(32)

磁链相角φfE来自于虚拟的三相参考电压，旋转频率为额定电压频率fn，不随相角δ变化，从而可以以很小的频率偏差实现有功分配。

4 仿真建模与分析

为了验证本文提到的基于DFC的下垂控制策略的有效性，利用MATLAB/Simulink搭建了图7所示的简化微网模型，表3为系统参数[15]。

图7 带有两个并联逆变器的简化微网模型Fig.7 Simplified microgrid model with two parallel inverters

参数数值直流侧电压Vdc1，Vdc2/kV10线路电感L1，L2/mH8线路电阻R1，R2/Ω005滤波电容C1，C2/μF150负载电感L11，L22/mH40负载电阻1R11，R21/Ω16负载电阻2R12，R22/Ω30连接线电感Lt/mH6连接线电阻Rt/Ω04额定线电压En/kV36额定频率fn/HZ60额定磁链幅值|ψV|n/Wb7797额定相角差δn/rads02DG1额定有功功率P1n/MW075DG1额定无功功率Q1n/MVar02DG2额定有功功率P2n/MW06DG2额定无功功率Q2n/MVar01DG1的P-δ斜率mf1/rad·W-1-267×10-7DG1的Q-|ψ|斜率nf1/Wb·Var-1-265×10-7DG2的P-δ斜率mf2/rad·W-1-333×10-7DG2的Q-|ψ|斜率nf2/Wb·Var-1-955×10-7

t=0.2 s时，将R22减小为原值的一半，图8(a)和图8(b)分别为DG1和DG2的功率分配情况。从图中可以看出DG1比DG2承担更多的功率,这是因为DG1的下垂系数较DG2更大。当有功负载发生改变时，分布式电源能在20 ms内迅速调整有功功率输出以适应负载变化，而无功功率几乎不变。

图8 两个分布式电源的功率分配情况Fig.8 Active and reactive power sharing of DGs

图9(a)和9(b)分别为DFC改进前后的磁链轨迹图。从图中可以看出，采用传统6扇区划分时，磁链轨迹为不规则圆形，脉动比较大。而采用改进的12扇区划分时，磁链轨迹近似为圆形，提高了磁链控制性能，从而间接提高了电压质量。

图9 DFC改进前后的磁链轨迹图Fig.9 Flux trajectory before and after DFC improvement

图10为DG1负载侧输出电流，从图10中可以看到电流的波形是正弦稳定的，并且在负载变化后能够迅速达到新的稳定状态。

图10 负载侧输出电流Fig.10 Output current of load side

图11(a)和11(b)分别表示DG1负载侧输出三相和单相电压波形。按照公式(32)计算，相电压的幅值约为3 000 V。从图11中可以看到，负载变化前后，负载侧电压都是非常稳定的正弦波。从图12可以看到，电压的畸变率很小，总畸变率只有0.57%。DG2的电流与电压波形与DG1类似,这里不做分析。

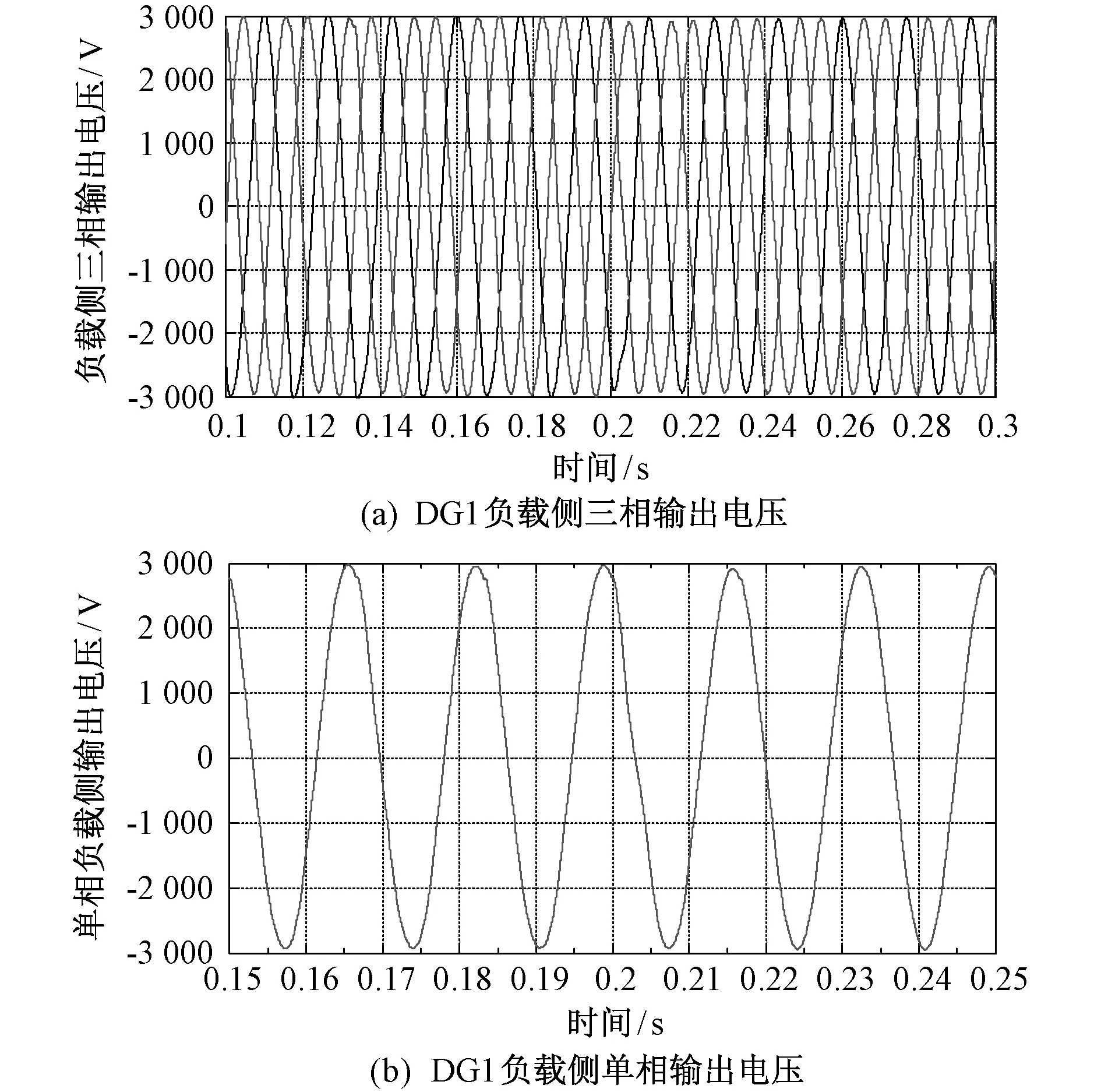
图11 负载侧输出相电压Fig.11 Output phase voltage of load side

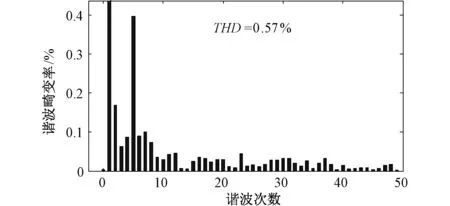
图12 负载侧电压的畸变情况Fig.12 Distortion of load side voltage

图13(a)和13(b)为不同控制策略下的系统频率特性。从图13(a)中可知：在传统的下垂控制中，负载变化后的频率偏差为0.4HZ,约为额定频率的0.7%。而从图13(b)中可知，采用磁链下垂控制策略时，频率在额定频率附近波动，这是由相角δ在滞环范围内的波动引起的。但是由于相角δ被紧密控制，故频率变化范围很小，最大的频率偏差仅为额定频率的0.3%，并且当系统稳定后偏差近乎为零。这证明了通过相角控制有功确实能够降低频率的偏差，提高电能质量。

图13 两种下垂控制策略下的系统频率特性Fig.13 System frequency characteristic of microgrid under two kinds of droop control strategies

5 结 论

针对传统电压下垂控制的局限性，本文研究了基于虚拟磁链的下垂控制方法，设计了改进的直接磁链控制器。最后通过对本文所提控制策略的仿真验证得出了以下结论：

(1)与传统的电压下垂控制策略相比，基于DFC的磁链下垂控制实现简单，频率偏差更小。

(2)在磁链下垂控制策略中，改进的直接磁链控制器减小了磁链的脉动性，提高了磁链的控制性能。

(3) 基于DFC的磁链下垂控制策略具有良好的动态响应，负载变化时，能够迅速调整功率输出适应负载变化。同时，该控制策略具有良好的静态稳定性，输出电压和电流均为稳定的正弦波，谐波畸变率很小。

[1] 鲁宗相，王彩霞，闵勇，等.微电网研究综述[J].电力系统自动化，2007，31(9):25-34.

[2] TULADHAR A, JIN H, UNGER T, et al. Control of parallel inverters in distribute AC power system with consideration of line impedance effect [J].IEEE Transactions on Industrial Application,2000,36(1):131-138.

[3] LI Yunwei, VILATHGAMUWA D M, LOH P C. Design, analysis， and real-time testing of a controller for multibus microgrid system[J]. IEEE Transactions on Power Electronics, 2004,19(5):1195-1204.

[4] AHN S J, PARK J W, CHUNG I Y, et al. Power-sharing method of multiple distributed generators considering control modes and configurations of a microgrid [J]. IEEE Transactions on Power Delivery,2010,25(3):2007-2016.

[5] 荆 龙，黄 杏，吴学智. 改进型微源下垂控制策略研究[J].电工技术学报，2014，29(2):146-153.

[6] 张东，卓放，师洪涛，等. 基于下垂系数步长自适应的下垂控制策略[J].电力系统自动化，2014，38(24):20-25.

[7] 谢永流，程志江，李永东，等. 基于新型下垂控制的逆变器孤岛并联运行研究[J].电测与仪表，2016，53(10):39-43.

[8] 郜登科，姜建国，张宇华. 使用电压—相角下垂控制的微电网控制策略研究[J]. 电力系统自动化，2012，36(5):29-34.

[9] LI Y， KAO C N. An accurate power control strategy for power electronics-interfaced distributed generation units operating in a low voltage multibus microgrid[J].IEEE Transactions on Power Electronics,2009,24(12):2977-2988.

[10] 廖晓钟，邵立伟.直接转矩控制的十二区段控制方法[J].电机工程学报，2006，26(6):167-173.

[11] 舒杰，张先勇，沈玉梁.基于虚拟磁链的微电网分布式逆变电源的功率平衡控制[J].中山大学学报，2010，49(1):60-64.

[12] 张守一. 分布式发电微网系统建模及控制策略研究[D]. 北京：北京交通大学，2014.

Research on Droop Control Strategy for Parallel Inverters Based on Direct Flux Control

WANG Aimeng, ZHANG Jia

(School of Electrical and Electronic Engineering, North China Electric Power University, Baoding 071003, China)

Conventionally, power budget by voltage-frequency droop method needs complicated multiple loop control and Park transformation, with greater deviation of frequency. Considering the problem, this paper provides droop control method based on virtual flux, which can adjust power by means of flux linkage-phase angle droop control. Then an improved direct flux linkage controller based on Direct Flux Control (DFC) Theory is designed. The controller with simple control operation, rapid dynamic response and small flux ripple, succeeds in controlling the phase angle and amplitude of flux linkage and replaces the multiple feedback loop and PI regulators in conventional droop control. Finally, taking advantage of MATLAB/Simulink software, a simplified micro-grid model with two parallel converters is established to testify the validity of the designed control strategy. The simulation result shows that the control strategy possesses favorable dynamic response and static stability, with smaller frequency deviation compared with conventional droop control method.

microgrid; droop control; virtual flux; direct flux control(DFC)

10.3969/j.ISSN.1007-2691.2017.05.09

TM315

A

1007-2691(2017)05-0062-00

2016-12-05.

河北省自然科学基金资助项目(E2012502018)；新能源电力系统国家重点实验室开放课题(LAPS16023).

王艾萌(1963-)，女，教授，研究方向电机设计及其控制技术；张佳(1990-)，女，硕士研究生，研究方向为新能源发电及微网控制技术。