流域梯级水电优化调度模型与方法研究综述

刘 方， 张粒子

(华北电力大学 电气与电子工程学院，北京 102206)

流域梯级水电优化调度模型与方法研究综述

刘 方， 张粒子

(华北电力大学 电气与电子工程学院，北京 102206)

我国大水电集中投产，形成大型流域梯级水电站群，使得如何做好梯级水电站群的调度运行工作，实现大范围资源优化配置显得尤为重要。阐述了我国水电发展现状；根据梯级水电在不同时间尺度下的运行特征和任务需求，对中长期/短期调度、日前调度和实时调度的目标函数与约束条件进行总结。优化算法方面，探讨了优化调度模型降维方法，重点分析了动态规划算法、遗传算法、粒子群算法的并行特征，并介绍了并行计算技术的实际应用。最后，针对未来梯级水电参与电力市场面临的问题及后续研究方向给予展望。

梯级水电站； 优化调度； 优化方法； 并行计算； 电力市场

0 引 言

经过多年“流域、梯级、滚动、综合”开发，我国水电快速发展，逐步形成特大流域和干流梯级水电站群[1-3]，使得做好梯级水电站群投产并网后的优化调度工作，大范围优化配置水电资源，充分发挥其社会经济效益，成为亟待解决的问题。

梯级水电站出力受径流年际、年内周期变化影响，丰、枯季节明显，根据库容调节能力和径流预测合理安排中长期出力计划，有利于缓解丰水期容量短缺与枯水期水量匮乏的矛盾。水电机组运行灵活，可在数分钟内实现启机到满发的大范围变负荷运行，是优良的备用、调峰和调频电源[4, 5]。因此，根据水电站运行特征安排不同时间尺度的调度计划，促进水电资源利用，亦有助于电力系统稳定运行。

梯级水电站优化调度模型具有多阶段、带时滞、非线性等特点，且随着电站数目的增多，以及为获取更高精度解而增加时段状态变量离散数，使得计算时间呈指数增加，“维数灾”问题愈发严重[6, 7]。为提高求解效率，在原有算法基础上精细化改进、降低优化调度模型维数，或引入多核并行计算、集群计算等新兴计算技术，成为一些学者深入研究的热点。

本文阐述了我国水电发展现状，根据不同时间尺度下梯级水电运行特点和调度需求，对中长期/短期调度、日前调度和实时调度的优化目标、约束条件及具体任务需求进行归纳总结。在优化调度方法方面，探讨了水位约束空间收缩方法和系统分解协调方法在调度模型降维方面的具体应用；讨论了传统优化算法和智能算法的适应性，并深入分析了动态规划方法、遗传算法和粒子群算法的并行特征，以及Fork/join并行框架、MapReduce并行编程机制、Matlab集群并行计算框架的应用。最后，对未来梯级水电参与电力市场面临的问题及后续研究方向给予展望。

1 我国水电发展现现状

我国幅员辽阔，水力资源蕴藏丰富，理论蕴藏量在1万kW以上的河流3 886条，装机容量5.42亿kW，年电量6.08万亿kW·h，技术可开发年发电量2.47万亿kW·h，理论蕴藏量和技术可开发量分别占全球总量的15%和17%，均居世界首位[8]。我国水力资源富集于大江大河干流，有助于“流域、滚动、梯级、综合”开发，规模效益显著，形成的“十三大水电基地”技术可开发装机容量约2.78亿kW，年发电量1.216亿kW·h，分别占全国总量的51.4%和49.1%[9, 10]。“十三大水电基地”规划见图1，规划装机规模和年发电量见图2。

图1 “十三大水电基地”规划图Fig.1 Planning map of Thirteen Larger Hydropower Basin

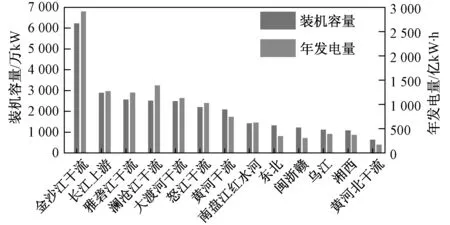
图2 “十三大水电基地”规划装机容量和年发电量Fig.2 The planned installed capacity and annual power generation of Thirteen Larger Hydropower Basin

2020年前，我国水电主要依托开发“十三大水电基地”扩大装机规模。“十二五”期间为“十三大水电基地”主要干流开发高峰期，投产容量集中在金沙江中下游、雅砻江下游、大渡河及澜沧江等基地，截止2015年底，全国水电装机容量为3.2亿kW，约占全球水电总装机的27%。随着以向家坝、溪洛渡、锦屏一级/二级、糯扎渡为标志的巨型水电站投产，以及配套“复奉”、“宾金”、“锦苏”、“普侨”±800 kV特高直流输电工程投运，“西电东送”南通道和中通道总输电能力超过6 867万kW[9]，水电进入远距离、跨省跨区大规模调度消纳新阶段。“十三五”期间水电继续保持合理建设规模，预计2020年水电总装机达3.8亿kW，包括常规水电3.4亿kW和抽水蓄能电站4 000万kW，年发电量可达1.25万亿kW·h[11]，“西电东送”战略继续推进，加强南部、中部、北部输电通道建设，实现更大范围水电消纳和能源结构优化。

2 梯级水电优化调度模型

梯级水电优化调度按时间尺度可分为中长期调度、短期调度、日前调度和实时调度。中长期调度根据年内、年际径流预测和互联电网负荷特性安排年度甚至跨年出力计划[12, 13]；短期调度通常以月度/季度为调度周期，侧重于将中长期出力计划分解到各日/周时间粒度，并根据短期径流和负荷预测调整中长期调度计划；日前调度根据次日负荷曲线预测，以满足系统安全运行要求安排次日最优开机组合及出力计划；实时调度侧重于将调度中心下达的日前负荷计划精细化分配到各机组，优化机组出力和启停顺序，降低水耗，节约水资源，属于“以电定水”范畴。

梯级水电中长期调度、短期调度时间尺度长，均是根据径流预测安排出力计划，属于“以水定电”过程，优化目标和约束条件具有一定的共性，本文将中长期/短期一起讨论，对日前调度和实时调度分别讨论。

2.1中长期/短期优化调度

2.1.1 目标函数

梯级水电站群中长期/短期优化调度通常在考虑水电站承担的社会职能、机组检修安排等情况下，充分利用水库调蓄能力，实现周期内发电量最大[14]：

(1)

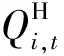
(2)

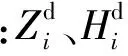
提高水电资源利用是国家节能减排的重要战略，为此一些研究将水电站蓄能利用最大化[15]作为中长期优化目标，文献[16]在水火电系统联合优化调度中以最小弃水量、系统污染排放最低为目标，有效提高水电资源利用效率。梯级水电站机组出力受限于水库调蓄能力和径流丰枯变化，为避免不同时段出力大幅调整影响系统电力电量平衡，文献[17]将最大保证出力作为调度目标，以适应不同来水年份，对保障水电装机比重较大省级电网安全尤为有利。电力市场环境下，水电上网价格由水电企业作为独立“经济人”参与市场竞争决定，决策目标通常在最大发电量目标中添加价格因子，构成发电效益最大化模型[18]。

在梯级水电多目标优化调度中，各子目标之间往往彼此冲突，难以同时达到最优，需要协调折中处理。可采用价格惩罚因子法、加权求和法等将多目标函数转换为单目标函数，但其惩罚因子和权重系数的确定经常受主观因素影响，也有研究采用模糊数学解决多目标优化问题，通过隶属度函数[16]出力多目标函数，在量纲不同、数量级不等情况下更为实用。文献[19]在水火电联合系统优化调度中，根据最小火电能耗、最小SO2排放和最大龙头水库期末蓄水量目标函数隶属度求取一组非劣解作为最大模糊满意度，实现多目标合理折中。

2.1.2 约束条件

梯级水电站中长期/短期优化调度通常考虑的约束条件包括：(1)水量平衡约束，保证水电站自身时间维度和梯级间空间维度的水量平衡；(2)库水位约束，上限水位在汛期设为汛限水位，其他时段为正常蓄水位，下限水位根据调度需要设置相应的消落控制水位；(3)发电流量约束，上限值为依机组过流能力设置，下限值根据保证出力或航运基流设定；(4)水库下泄流量约束，根据通航、灌溉、防洪和综合用水需求设定；(5)水电站出力约束，最大值为机组额定总出力，最小值为保证出力；(6)出力破坏深度约束，以避免出现极端气候时出力破坏深度过大影响电网运行安全。

除上述约束外，一些研究将水电带宽约束[20]、发电保证率约束[17]等约束融入优化调度模型，使研究结果更切近实际。在月度电量分解模型中，通过典型日电力电量平衡校验确保月度电量均衡，需要考虑典型日电力电量平衡约束，月度电量约束及年度总电量平衡约束[21]。

2.2日前优化调度

2.2.1 目标函数

由于目前电力大规模存储技术尚不成熟，经济性欠佳，发、输、配、变、用各个环节必须瞬间完成，为保证电力系统实时平衡，安排日前调度获取与系统实际相接近的运行方式。水电机组运行灵活，大范围变负荷运行能力强，除汛期避免弃水而满载出力承担基荷外，日前调度中往往被安排跟踪负荷波动参与系统调峰[22, 23]，使其他调节性能欠佳电源承担的余荷尽可能平稳，提高全系统运行效率，保障电网安稳运行。因此，梯级水电站日前调度通常采用调峰电量最大模型，以水电调节后的剩余负荷峰值最小构建目标函数[24]，可表示为

(3)

式中：Ct为第t时段的系统负荷,MW；Pi,t为水电站i在时段t的平均出力,MW。

我国“西电东送”网架规模不断扩大，西南大水电投产后，经超/特高压直流输电通道远距离、大容量馈入华东、广东等负荷中心。由于装机容量巨大，面临同一流域上、下游水电站向多电网以及单一水电站向多电网送电的问题[25]。根据多受端电网日负荷特性、区外电消纳能力差异，以及送受端各类电源特性差异，挖掘电力互济空间，提高汛期水电消纳规模；发挥跨流域梯级水电站群补偿调节效益缓解受端电网调峰压力[9]。文献[26]以各省级电网余荷与理想余荷的差值平方和构建电网调峰目标函数，优化分配外来电力电量，满足多网调峰要求；文献[27-29]提出了网省两级协调电力控制和电量控制方式，通过按需供给和多电源互补，提高特高压直流水电消纳规模，遵循省网合同电量且提高了电网负荷平均调峰率，改善现行省网之间依靠协议或经验分配电力以及直流水电固定电力输送方式的不足；文献[30]将多省级电网负荷曲线重构为一条总负荷曲线，在此基础上采用变尺度方法优化梯级水电站出力及受端电网间负荷分配，实现多电网调峰；文献[31]从厂网协调的角度出发，考虑电网受电量、梯级水电站调峰容量及高压直流输电线路稳定运行限制，利用网间负荷互补特性，优化计算受端电网最佳受电计划；文献[32]考虑峰、平、谷不同时段负荷需求和分时电价变化，优化调节性水电站出力过程，“低储高发”追踪电价波动，提高控制期内发电效益的同时迎合系统调峰需求。

2.2.2 约束条件

梯级水电站日前调度模型约束条件中，除水量平衡约束、水电机组出力约束、库水位约束、发电流量约束外，还需要考虑如下约束：(1)机组爬坡约束；(2)启停机最小持续时间约束，避免水电机组频繁启停，影响寿命；(3)电站出力波动控制约束[24]，避免出力频繁大幅调整；(4)不可运行区约束[4]，避免机组运行在振动区和汽蚀区，确保生产安全；(5)调度时段末控制水位约束，参考中长期/短期调度计划电量分解设定。

对于电网中承担调峰任务水电站，发电流量变化迅速，容易引起下泄流量和水位的波动，影响航运、灌溉等综合用水，一些水电站在下游兴建反调节水库联合调度以平抑流量波动[33]，但均需要考虑如下约束：下游生态流量约束，以满足下游河道通航、取水和生态环境要求；断面流量变幅约束和水位时变约束，以避免下泄流量忽涨忽落影响水流态势。在跨省跨区直流送电并承担受电区调峰责任的水电站调度模型中还需要考虑：电力电量平衡约束、电站多电网送电量比例约束[31]、各电网受电量控制需求约束[30]、直流输送控制约束、输送功率上下限约束、输送功率变幅限制约束[27]。

各梯级水电站之间具有一定的水流时滞[34]，在中长期/短期时间尺度内，水流时滞对上、下游水电站之间的水量平衡制约不明显，可予忽略。日前调度中，当水流时滞尺度较大时，下游水电站出力计划将向调度期前段聚集，入库流量向调度期后段聚集，造成下游水库水量失衡甚至约束破坏，影响下游水电站日前调度计划的执行，尤其在下游水电站调节性能欠佳情况下更为明显。针对于此，文献[35]重点考虑了上、下游水电站之间的水流时滞对日前调度计划的影响，将上周期时滞带来的转入效益纳入本周期发电效益中，并将本周期对后一周期的转出效益予以剔除，优化结果更符合实际情况。

2.3实时优化调度

2.3.1 目标函数

梯级水电站实时调度将调度中心日前安排的负荷任务精细化分配到各机组，并跟踪实时负荷需求调整出力。因此，实时调度旨在满足电网电力平衡要求的同时降低发电水耗，增加系统蓄能[36]。梯级水电站最大蓄能优化目标描述为

(4)

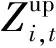
2.3.2 约束条件

梯级水电站实时调度中，除需要考虑水量平衡约束、机组出力约束、库水位约束、发电流量约束、不可运行区约束、机组爬坡约束外，还需考虑：电站过流能力约束、机组出力受阻限制等约束。在确定最优库水位和出库流量过程中，由于出库流量增加将抬高尾水位，当出库流量增加到一定值时，过机流量增加的出力不足以弥补尾水位抬高损失的水头效益，继续增加出库流量反而阻碍水电站出力，需精确计算水电站出库流量经济上限，尽量避免泄流增加反而出力降低的现象。

3 优化调度方法

3.1优化调度模型降维方法

水电站数目增加以及求解精度需求的提高，使梯级水电优化调度模型更加复杂，“维数灾”问题愈发突出[7, 37]，一些学者尝试从调度模型处理入手，制定行之有效的降维策略，以期获取理想的计算效果。主要应用方法有：水位约束空间收缩方法和梯级水电系统分解协调方法。

(1)水位约束空间收缩方法

调度过程中，根据预测径流及上下游用水需求设置水位约束，该约束区域或将包含不可行域，造成寻优空间过大，计算资源浪费。可根据水电站保证出力和下泄流量约束来辨识有效水位约束空间，去除不可行域的影响[38]，描述如下：水电站在入库流量固定情况下，出力与前池水位和发电流量有关，可近似认为出力随发电流量单调递增，因此需下泄流量大于某个临界值Qf时，可满足保证出力，且此时综合用水通常能满足，Qf即为水电站最小综合下泄流量；水库起调水位和周期末水位设置相等，则水位变化应在按照Qf分别以起调水位前推和周期末水位倒推得到的水位上、下确界内。将上、下确界与原水位约束取交集形成收缩水位约束空间，大大缩减了寻优空间；寻优过程中，若水位超出该约束空间，则置为约束边界值。该从周期始、末端逐时段计算的有效约束空间，约束值呈现平滑变化，相比于原约束为一系列离散值，更加体现水库水位随流量吞吐，相邻时段呈连续变化的耦合关系。

(2)梯级水电系统分解协调方法

分解协调方法主要基于大系统分解协调思想[39]对梯级水电系统进行分区调度并协调优化，以缓解“维数灾”问题。大系统分解协调方法是将大系统暂时分解为若干独立子系统，并分别寻求局部最优解，该层称为系统分解层；在各子系统最优解基础上，恢复各子系统之间耦合关系，并通过耦合变量进行更高级协调，达到全系统最优，该层称为系统协调层[40]。该方法一般先由协调层对分解层给定协调变量值，然后各子系统经各自优化决策后，向协调层送回反馈变量，协调层根据反馈变量修正协调变量后再次反馈给分解层，反复迭代直到全系统最优。分解和协调是密切相关的两个基本过程，其递阶示意图见图3所示。

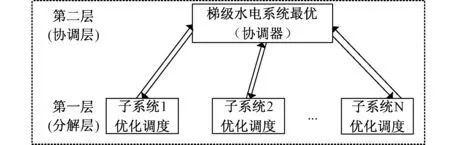
图3 分解协调递阶示意图Fig.3 Schematic diagram of decomposition and coordination

依托大系统分解协调思想，文献[38]依据水电站所属流域相对位置将梯级水电系统分解成若干子系统，虑及各子系统之间水力联系，逐级计算实现整个梯级水电站群最优，有效降低计算规模，且分解过程中根据地理位置虚拟分区，对我国多支流或跨省区开发的流域梯级水电站群更具有适用性；文献[39]以单个水电站为独立子系统进行优化协调，计算精度和效率较高，满足实际运行需求，尤其在水电站之间水力、电力弱耦合联系不够密切的情况下效果更明显。

3.2优化算法

随着现代计算机技术和人工智能理论的发展，各种新模型与算法相继出现，梯级水电优化调度常用算法可分为2大类：传统优化算法和智能算法。

(1)传统优化算法

传统优化算法以运筹学和最优化理论为基础，发展和应用较为成熟，常用方法有：Lagrange松弛法、网络流规划法、动态规划算法、线性规划法、非线性规划、混合整数规划、三角旋回算法等。其中，动态规划为多阶段决策的递推优化方法，无需初始决策，求解非线性、非凸和离散变量的优化问题可收敛于全局最优解，在梯级水电站群优化调度应用最广[41]，但需要线性化处理非线性目标函数和约束条件，弱化了梯级水电站间的水力耦合关系及问题本身的复杂性，求解精度受损。此外，为使求解效率难适应梯级水电群规模发展，国内外学者对动态规划进行了改进，取得了一些成果，主要有逐次逼近动态规划、微分动态规划[6]、正交离散微分动态规划[42]、逐歩优化算法[43]等。

(2)智能算法

水电站群调度决策变量与状态变量之间通常呈隐性和非线性关系，具体函数往往难以准确描述，智能算法结构灵活、映射能力强，对模型无任何限制，可直接求解多维、非连续、非线性等复杂优化问题，在梯级水电站群优化调度应用中表现出优良性能。

智能算法一般是在循环迭代中模拟生物进化、迁徙、觅食等自然行为搜寻最优解，经常应用在梯级水电优化调度算法主要有：蚁群优化算法、遗传算法、差分进化算法、模拟退火算法、粒子群算法、人工神经网络等。国内外学者针对实际应用中容易陷入局部最优、寻优能力欠佳等问题进行改进，提出了改进量子粒子群算法[20]、自适应混合粒子群算法[44]、分层遗传算法[45]等，大幅度提升算法寻优性能。此外，近年来学者提出的新颖启发式全局优化算法亦被应用于梯级水电调度，如：精英集聚蛛群优化方法[46]、布谷鸟算法[47]、群居蜘蛛优化算法[48]等。

4 并行计算方法

随着梯级水电系统电站数目的增多，优化调度模型中参与计算的状态变量和决策变量数目成倍增加，计算规模呈指数增长，计算耗时和精度难以满足工程应用需求，寻求高效计算方法和技术成为学者关注的焦点[39]。

多核处理器的普及并行技术研究的不断深入使并行计算作为一项有效提高计算性能的技术得到广泛应用。并行计算是将一个大规模计算任务分解成多个独立子任务并分配到不同处理器中，调用多处理器协同工作、同步执行[49]，以提高计算效率和求解精度。其中，计算子任务的独立性以及计算顺序与最终结果的无关性是实现并行计算的必要条件。

4.1Fork/Join并行计算框架

Fork/Join并行计算框架在梯级水电优化调度领域应用较为成熟[17, 50, 51]，基于“分而治之”思想，主要通过Fork和Join两种操作：Fork操作负责对复杂任务分解为多个彼此独立的子任务，并将子任务分配到CPU多核心执行并行计算；Join操作用于阻塞当前任务，直到其子任务计算完成，返回结果后整合为整体任务结果。Fork/Join框架见图4。Fork/Join框架采用线程池技术，默认创建的线程数为CPU内核数，节约每次线程创建和关闭占用的系统资源。“工作窃取”线程调度机制是Fork/Join框架的核心：当一个线程执行完自身任务队列中全部任务后，会窃取其他线程任务队列尾端未执行的任务协助执行，从而合理均衡各线程负载，节约同步执行时间。各线程间通信通过开辟共享数据缓存区，利用Java线程同步和通信机制来实现。

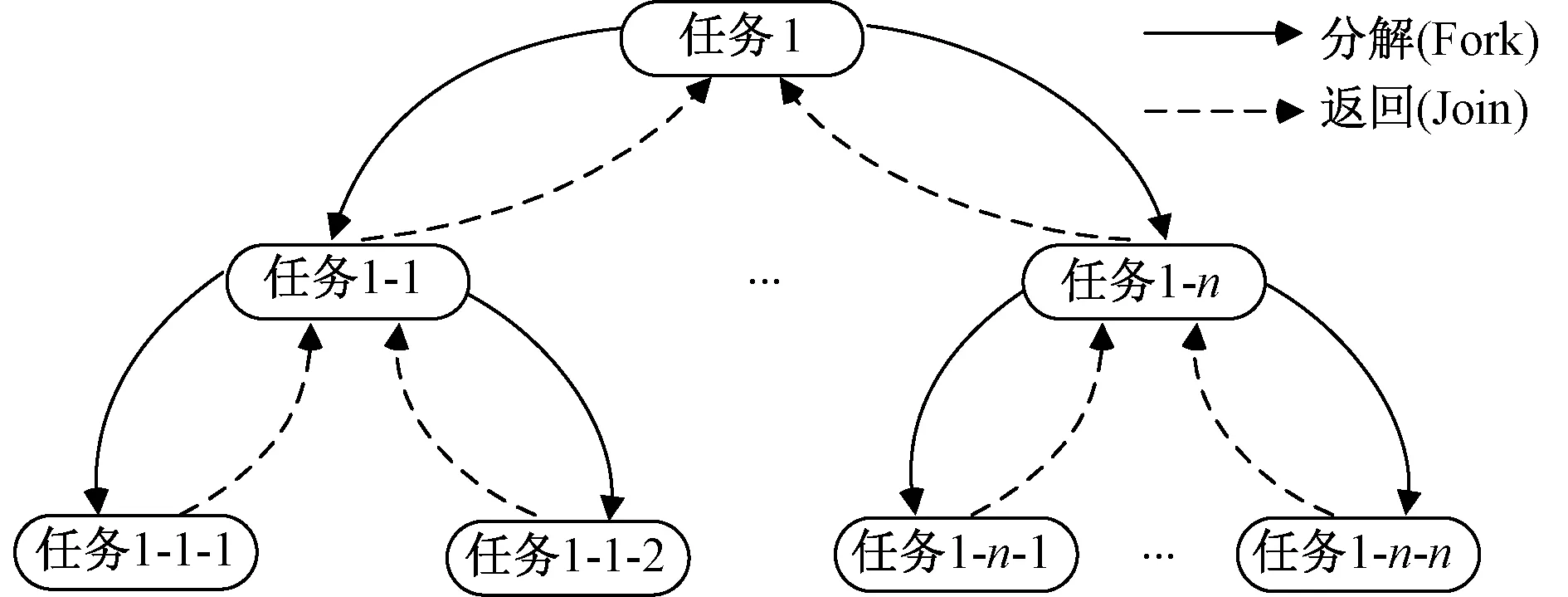
图4 Fork/Join框架计算模型Fig.4 The Calculation model of Fork/Join frame

4.2动态规划并行计算

标准动态规划求解梯级水电优化调度时，计算流程中包含三层循环：最外层为阶段变量循环，即为整个调度期内的优化时段循环；中间层为状态变量循环，即为各优化时段末库水位离散值的遍历循环；最内层为决策变量循环，即为优化时段末库水位处于某离散值时的发电流量计算循环。在阶段变量固定时，进行中间层的状态变量离散点遍历循环中，各离散点具有相对对立性，求解顺序不影响当前时段的寻优结果。因此，可以将中间层对离散点的遍历任务处理为分段并行进行，挖掘状态空间的并行性。

针对动态规划可将任务分解进行并行计算的特征，文献[39]利用多线程编程技术控制CPU资源，并行化处理标准动态规划算法求解单库调度问题；文献[52]构建多维动态规划模型求解水库群优化调度问题，计算时间有效缩短且加速比随核数增加而提升；程春田教授等人提出了多核并行随机动态规划方法[53]和细粒度并行离散微分动态规划方法[6]，基于Fork/Join并行框架应用于梯级水电站长期发电量最大模型的求解，执行效率提升显著。

4.3智能算法并行寻优

研究新算法或对已有遗传算法、粒子群算法、人工神经网络等智能算法改进来提升梯级水电站群优化调度求解效率愈发困难，一些学者尝试利用一些智能算法可并行寻优的特征进行分布式并行编程，提高计算效率和精度，成为梯级水电优化调度研究的新方向[54]。

4.3.1 并行遗传算法

遗传算法并行性改进可从群体分组的并行计算入手，利用各种群彼此独立的特征，按一定规律独立寻优，互不影响，与自然界生物并行进化的实际情况相符合。遗传算法并行模型主要有：主从式模型、粗粒度模型、细粒度模型。主从式模型将系统分为一个主处理器和若干从处理器，主处理器监控整个染色体种群，执行全局选择操作，各从处理器接受主处理器选择的种群执行交叉和变异，产生新一代种群并计算适应度。细粒度和粗粒度并行模型的区别在于：粗粒度模型将种群划分为若干子种群，子种群独立进化，偶尔与临近子种群交换个体；细粒度模型将种群进行更精细划分，理想情况是各子种群仅1个染色体，相邻个体之间交流促进全种群进化[54]，细粒度模型需要处理器数量多，应用集群并行计算技术更具有优势。

将遗传算法并行性结合并行计算技术高执行效率，加快算法搜索进度，且扩大种群规模和子种群隔离，丰富并保持了种群多样性，有效提高对复杂问题全局寻优效率和精度，被众多学者应用于求解大规模梯级水电站群优化调度问题。文献[55]在粗粒度并行遗传算法中增加根据解的多样性自适应调节信息交流周期策略，并应用于雅砻江梯级水电站群优化调度；文献[56]将禁忌搜索策略及多核并行技术与遗传算法相结合，计算红水河库群长期优化调度，求解效率和质量满足工程需求。

4.3.2 并行粒子群算法

并行粒子群算法将粒子群体划分成若干彼此独立子群体，并分配到不同处理器并行寻优，通过周期地通信，共享群体最优位置，防止陷入局部最优。粒子群算法并行模型主要有：主从模型、岛屿模型、蜂窝模型。主从模型中，主处理器串行处理粒子初始化、粒子信息更新和汇总，各从处理器并行执行子群体适应度计算更新；岛屿模型中，粒子群划分为多个粒子组，并被分配到独立处理单元进行信息更新和适应度值计算，通过粒子转移策略促进全局信息的交换，避免粒子群过早收敛，各粒子组内粒子规模相对较大。蜂窝模型中粒子群分成多个粒子组，各粒子组由一个处理器执行，各处理器在二维网格中仅与周边4个处理器交换粒子信息，在粒子规模较小的情况下求解效果较好，但由于只进行邻边信息交流，全局信息在粒子组之间的传递将被延缓[57]。

并行粒子群算法在求解梯级水电站群优化调度中取得了理想的效果。文献[58]应用粗粒度并行粒子群算法求解水库群联合调度图模型，基于Fork/Join框架将子群体分配到不同CPU内核独立求解，并利用Java线程通信机制确保子群体间的信息交流，全局寻优效果较好；文献[59]在混沌量子粒子群算法中的混沌初始化种群、粒子群位置更新和精英粒子混沌局部搜索等过程中应用多核并行计算技术，以计算空间复杂度的适当牺牲换取算法执行效率的大幅提升。

4.4多核集群并行计算

传统并行机价格昂贵，阻碍了普通用户对并行计算技术的应用。用普通多核PC组建集群计算系统，结构灵活易于扩展，具有并行机的高计算性能，且实现容易投资省，成为并行计算机体系发展趋势之一。

在众多并行计算平台中，Hadoop开源平台能够对大量数据进行分布式并行处理，凭借高扩展性、高容错性及成本低廉等优势，深受分布式开发用户欢迎。Hadoop实现了MapReduce编程模型[60]，将计算任务分割成多个小工作单元分配到集群节点上执行，再将执行结果汇总，即映射(Map)和归约(Reduce)2个阶段：在Map阶段之前，将输入数据分割成固定大小的切片(split)，封装成若干键值对作为Map阶段的输入；各mapper并行处理后，将中间数据合并产生键值对再经过排序作为Reduce阶段的输入；最终由各reducer进行归约操作获取最终结果。MapReduce工作机制如图5所示。

图5 MapReduce工作机制Fig.5 The working mechanism of MapReduce

Matlab集矩阵运算、数值分析、图形信号处理于一体，其突出优势为强大的科学计算能力以及专用工具箱具备全面的数学函数，可并行处理大数据集，尤其在集群环境中优势更为凸显，被广大科研工作者广泛使用。Matlab并行计算工具箱(Parallel Computing Toolbox, PCT)和Matlab分布式计算引擎(Matlab Distributed Computing Engine, MDCE)共同为用户解决庞大数据集的计算密集性应用提供支持。PCT应用程序在客户端建立原型，通过MDCE扩展到多台计算机构建的分层存储结构集群进行计算。客户端通过PCT创建工作(job)，并将大计算量程序(job)分解为多个子任务(task)；MDCE用于完成客户端发来的job，负责执行所有task并将计算结果返回客户端。MDCE中的作业管理器(job manager)负责调度job、分配task、接收计算结果并向客户端反馈结果；计算单元(worker)执行job manager所分配task的计算结点，计算结果返回给job manager。Matlab多核集群并行计算框架如图6所示。

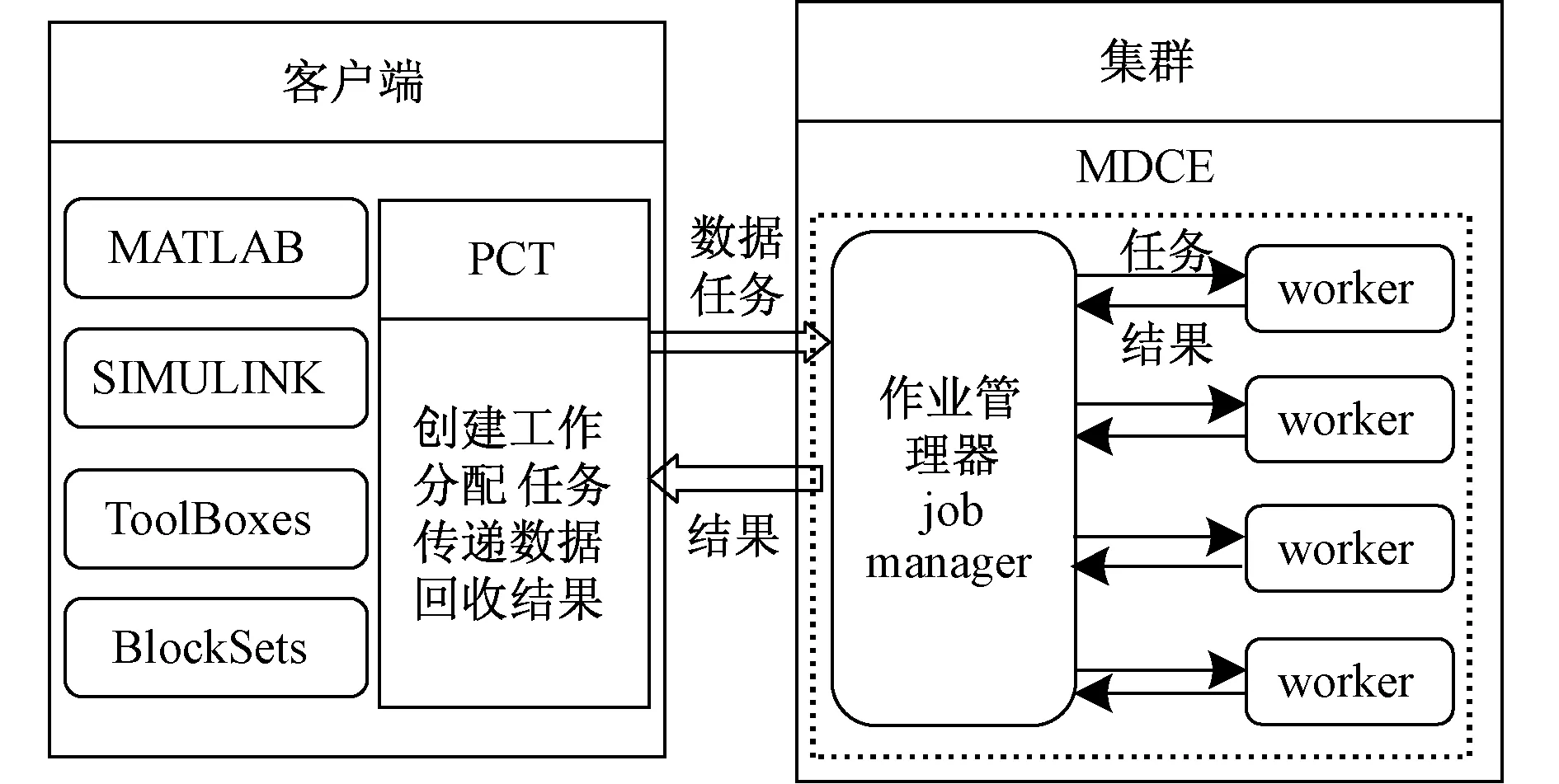
图6 Matlab多核集群并行计算框架图Fig.6 Matlab multi-core cluster parallel computing framework

基于Hadoop平台的MapReduce编程机制或matlab多核集群并行计算平台，只需拥有3台及以上计算机便可搭建多核集群并行计算环境，使集群中多台计算机同时参与计算，效果相当于多台计算机计算能力之和，有效整合闲置廉价计算资源，为研究大规模流域梯级水电站群优化调度提供便捷、高效的技术支撑。

5 结 论

本文结合我国梯级水电站群优化调度发展情况，主要从优化调度模型、方法等方面进行归纳总结，重点分析了梯级水电站群优化调度中的并行计算技术应用，并对多核集群并行计算技术适用性进行深入探讨。

目前，我国电力市场化建设不断推进，使梯级水电参与电力市场成为大势所趋。后续将深入研究梯级水电站在市场环境下的优化调度，重点针对同一流域上、下游水电站参与不同市场，以及同一水电站参与多市场的情况，考虑各水电站之间的水量平衡、水流时滞等水力联系，兼顾参与各市场多交易品种之间的均衡，实现全流域梯级水电站的运行优化、协调调度。

梯级水电站出力受径流季节丰枯变化影响，且多承担防洪、灌溉、航运等综合职能，参与电力市场将面临收益风险和电量不确定性风险，需要深入研究在考虑自身运行和市场变化情况下的多交易品种组合风险评估，选择不同类型、周期和方式的交易品种进行组合优化，解决单一交易品种风险集中问题。

[1] 樊启祥, 金和平, 翁文林, 等. 基于数字流域的梯级水电工程管理系统设计与应用实践[J]. 水力发电学报,2016, 35(1): 136-145.

[2] WANG Chao, ZHOU Jianzhong, LU Peng,et al. Long-term scheduling of large cascade hydropower stations in Jinsha River, China[J]. Energy Conversion and Management, 2015, 90:476-487.

[3] LU Peng, ZHOU Jianzhong, WANG Chao,et al. Short-term hydro generation scheduling of Xiluodu and Xiangjiaba cascade hydropower stations using improved binary-real coded bee colony optimization algorithm[J]. Energy Conversion and Management, 2015, 91:19-31.

[4] SIOSHANSI Ramteen. Optimized Offers for Cascaded Hydroelectric Generators in a Market with Centralized Dispatch[J]. IEEE Transactions on Power Systems, 2015, 30(2):773-783.

[5] SCHERER Lucas Giuliani, TAMBARA Rodrigo Varella, DE CAMARGO Robinson Figueiredo. Voltage and frequency regulation of standalone self-excited induction generator for micro-hydro power generation using discrete-time adaptive control[J]. IET Renewable Power Generation, 2016, 10(4):531-540.

[6] 程春田, 郜晓亚, 武新宇, 等. 梯级水电站长期优化调度的细粒度并行离散微分动态规划方法[J]. 中国电机工程学报,2011, 31(10): 26-32.

[7] FENG Zhongkai, NIU Wenjing, CHENG Chuntian,et al. Hydropower system operation optimization by discrete differential dynamic programming based on orthogonal experiment design[J]. Energy, 2017, 126:720-732.

[8] 全国水力资源复查工作领导小组. 中华人民共和国水力资源复查成果(2003 年总报告分册)[M]. 北京: 中国电力出版社, 2003.

[9] 程春田, 励刚, 程雄, 等. 大规模特高压直流水电消纳问题及应用实践[J]. 中国电机工程学报,2015, 35(3): 549-560.

[10] ZHOU Jianzhong, ZHANG Yongchuan, ZHANG Rui,et al. Integrated optimization of hydroelectric energy in the upper and middle Yangtze River[J]. Renewable and Sustainable Energy Reviews, 2015, 45:481-512.

[11] 国家能源局. 能源发展“十三五”规划(公开发布稿)[EB/OL].http://www.sdpc.gov.cn/zcfb/zcfbtz/201701/W020170117335278192779.pdf, 2016-12-26/2017-4-8.

[12] 张粒子, 杨阳. 考虑年末预留水位的全景梯级水电跨年随机调度策略及模型[J]. 中国电机工程学报,2014, 34(1): 79-86.

[13] ZHAO Tinghong, MAN Zibin, WANG Yu,et al. Optimize dispatchers of Cascade hydropower station based on IS-NGA[C]. International Conference on Intelligent System Design and Engineering Applications, Hong Kong(CN), 2013:1038-1041.

[14] 冯仲恺, 廖胜利, 牛文静, 等. 梯级水电站群中长期优化调度的正交离散微分动态规划方法[J]. 中国电机工程学报,2015, 35(18): 4635-4644.

[15] MU Jie, MA Chao, ZHAO Jiaqing,et al. Optimal operation rules of Three-gorge and Gezhouba cascade hydropower stations in flood season[J]. Energy Conversion and Management, 2015, 96:159-174.

[16] 邓创, 鞠立伟, 刘俊勇, 等. 基于模糊CVaR理论的水火电系统随机调度多目标优化模型[J]. 电网技术,2016, 40(5): 1447-1454.

[17] 王森, 武新宇, 程春田, 等. 梯级水电站群长期发电优化调度多核并行机会约束动态规划方法[J]. 中国电机工程学报,2015, 35(10): 2417-2427.

[18] 贾江涛, 管晓宏, 翟桥柱. 考虑水头影响的梯级水电站群短期优化调度[J]. 电力系统自动化,2009, 33(13): 13-16.

[19] 吴杰康, 唐力. 基于模糊机会约束规划的水火电力系统多目标随机调度模型[J]. 中国电机工程学报,2011, 31(25): 26-34.

[20] 冯仲恺, 廖胜利, 牛文静, 等. 改进量子粒子群算法在水电站群优化调度中的应用[J]. 水科学进展,2015, 26(3): 413-422.

[21] 原文林, 曲晓宁, 方洪斌, 等. 基于风险偏好的梯级水电站合约电量月度分解模型研究[J]. 水力发电学报,2014, 33(3): 61-67.

[22] LU Di, WANG Bende, WANG Yaodong,et al. Optimal operation of cascade hydropower stations using hydrogen as storage medium[J]. Applied Energy, 2015, 137:56-63.

[23] SHEN Jianjian, CHENG Chuntian, CHENG Xiong,et al. Coordinated operations of large-scale UHVDC hydropower and conventional hydro energies about regional power grid[J]. Energy, 2016, 95:433-446.

[24] 申建建, 程春田, 李卫东, 等. 复杂时段耦合型约束水电站群短期变尺度优化调度方法[J]. 中国电机工程学报,2014, 34(1): 87-95.

[25] 武新宇, 程春田, 申建建, 等. 大规模水电站群短期优化调度方法Ⅲ:多电网调峰问题[J]. 水利学报,2012, 43(1): 31-42.

[26] 孟庆喜, 申建建, 程春田, 等. 多电网调峰负荷分配问题的目标函数选取与求解[J]. 中国电机工程学报,2014, 34(22): 3683-3690.

[27] 程雄, 程春田, 申建建, 等. 大规模跨区特高压直流水电网省两级协调优化方法[J]. 电力系统自动化,2015, 39(1): 151-158, 232.

[28] 吴慧军, 申建建, 程春田, 等. 网省两级调度多电源短期联合调峰方法[J]. 中国电机工程学报,2015, 35(11): 2743-2755.

[29] SHEN Jianjian, CHENG Chuntian, ZHANG Jun,et al. Peak Operation of Cascaded Hydropower Plants Serving Multiple Provinces[J]. Energies, 2015, 8(10):11295-11314.

[30] 申建建, 程春田, 程雄, 等. 跨省送电梯级水电站群调峰调度两阶段搜索方法[J]. 中国电机工程学报,2014, 34(28): 4817-4826.

[31] 卢鹏, 周建中, 莫莉, 等. 梯级水电站群多电网调峰调度及电力跨省区协调分配方法[J]. 电网技术,2016, 40(1): 1-9.

[32] 左幸, 马光文, 梁武湖, 等. 免疫算法在水电站日前现货市场优化调度中的应用[J]. 水力发电学报,2006, 25(6): 21-25.

[33] CHEN Juan, ZHONG Pingan, ZHAO Yunfa. Research on a layered coupling optimal operation model of the Three Gorges and Gezhouba cascade hydropower stations[J]. Energy Conversion and Management, 2014, 86:756-763.

[34] TEEGAVARAPU Ramesh SV, SIMONOVIC Slobodan P. Simulation of multiple hydropower reservoir operations using system dynamics approach[J]. Water Resources Management, 2014, 28(7):1937-1958.

[35] 钟平安, 张金花, 徐斌, 等. 梯级库群水流滞后性影响的日优化调度模型研究[J]. 水力发电学报,2012, 31(4): 34-38.

[36] 王嘉阳, 程春田, 廖胜利, 等. 复杂约束限制下的梯级水电站群实时优化调度方法及调整策略[J]. 中国电机工程学报,2015, 35(17): 4326-4334.

[37] HELSETH Arild, FODSTAD Marte, MO Birger. Optimal medium-term hydropower scheduling considering energy and reserve capacity markets[J]. IEEE Transactions on Sustainable Energy, 2016, 7(3):934-942.

[38] 周建中, 张睿, 王超, 等. 分区优化控制在水库群优化调度中的应用[J]. 华中科技大学学报(自然科学版),2014, 42(8): 79-84.

[39] 吴昊, 纪昌明, 蒋志强, 等. 梯级水库群发电优化调度的大系统分解协调模型[J]. 水力发电学报,2015, 34(11): 40-50.

[40] 李纯龙, 周建中, 欧阳硕, 等. 基于改进分解协调的大规模水电站群优化调度[J]. 电网技术,2013, 37(12): 3445-3452.

[41] STEEGER Gregory, BARROSO Luiz Augusto, REBENNACK Steffen. Optimal bidding strategies for hydro-electric producers: A literature survey[J]. IEEE Transactions on Power Systems, 2014, 29(4):1758-1766.

[42] FENG Zhongkai, NIU Wenjing, CHENG Chuntian,et al. Hydropower system operation optimization by discrete differential dynamic programming based on orthogonal experiment design[J]. Energy, 2017, 126:720-732.

[43] CHEN Shijun, YAN Shang, HUANG Weibin,et al. A method for optimal floodgate operation in cascade reservoirs[C]. Proceedings of the Institution of Civil Engineers-Water Management, 2016:81-92.

[44] BAHMANI Firouzi Bahman, FARJAH Ebrahim, AZIZIPANAH Abarghooee Rasoul. An efficient scenario-based and fuzzy self-adaptive learning particle swarm optimization approach for dynamic economic emission dispatch considering load and wind power uncertainties[J]. Energy, 2013, 50:232-244.

[45] 张忠波, 吴学春, 张双虎, 等. 并行动态规划和改进遗传算法在水库调度中的应用[J]. 水力发电学报,2014, 33(4): 21-27.

[46] 冯仲恺, 牛文静, 程春田, 等. 梯级水库群优化调度精英集聚蛛群优化方法[J]. 水利学报,2016, 47(6): 826-833.

[47] MARICHELVAM M K, PRABAHARAN T, YANG X S. Improved cuckoo search algorithm for hybrid flow shop scheduling problems to minimize makespan[J]. Applied Soft Computing, 2014, 19:93-101.

[48] 王文川, 雷冠军, 邱林, 等. 群居蜘蛛优化算法在水电站优化调度中的应用及其效能分析[J]. 水力发电学报,2015, 34(10): 80-87.

[49] WARLAND Geir, HENDEN Arild Lote, MO Birger. Use of Parallel Processing in Applications for Hydro Power Scheduling-Current Status and Future Challenges[J]. Energy Procedia, 2016, 87:157-164.

[50] FENG Zhongkai, NIU Wenjing, ZHOU Jianzhong,et al. Parallel Multi-Objective Genetic Algorithm for Short-Term Economic Environmental Hydrothermal Scheduling[J]. Energies, 2017, 10(2):163.

[51] PENG Yong, PENG Anbang, ZHANG Xiaoli,et al. Multi-Core Parallel Particle Swarm Optimization for the Operation of Inter-Basin Water Transfer-Supply Systems[J]. Water Resources Management, 2016:1-15.

[52] 孙平, 王丽萍, 蒋志强, 等. 两种多维动态规划算法在梯级水库优化调度中的应用[J]. 水利学报,2014, 45(11): 1327-1335.

[53] 王森, 程春田, 武新宇, 等. 梯级水电站群长期发电优化调度多核并行随机动态规划方法[J]. 中国科学:技术科学,2014, 44(2): 209-218.

[54] 张东晓, 王静, 范炜, 等. 基于并行遗传算法的水电站群中期优化调度[J]. 电力自动化设备,2012, 32(12): 87-91.

[55] 陈立华, 梅亚东, 麻荣永. 并行遗传算法在雅砻江梯级水库群优化调度中的应用[J]. 水力发电学报,2010, 29(6): 66-70.

[56] 刘本希, 廖胜利, 程春田, 等. 库群长期优化调度的多核并行禁忌遗传算法[J]. 水利学报,2012, 43(11): 1279-1286.

[57] 何莉, 刘晓东, 李松阳, 等. 多核环境下并行粒子群算法[J]. 计算机应用,2015, 35(9): 2482-2485, 2518.

[58] 彭安帮, 彭勇, 周惠成. 跨流域调水条件下水库群联合调度图的多核并行计算研究[J]. 水利学报,2014, 45(11): 1284-1292.

[59] 邹强, 王学敏, 李安强, 等. 基于并行混沌量子粒子群算法的梯级水库群防洪优化调度研究[J]. 水利学报,2016, 47(8): 967-976.

[60] GU Rong, YANG Xiaoliang, YAN Jinshuang,et al. SHadoop: Improving MapReduce performance by optimizing job execution mechanism in Hadoop clusters[J]. Journal of Parallel and Distributed Computing, 2014, 74(3):2166-2179.

Review on Optimization Scheduling Model and Method of Cascaded Hydropower Stations

LIU Fang，ZHANG Lizi

(School of Electrical and Electronic Engineering, North China Electric Power UniversityBeijing 102206, China)

Because of the centralized putting in operation of large hydropower, large-scale groups of cascade hydropower stations have formed in China. The issues that how to schedule cascade hydropower station efficiently and how to achieve a wide range of optimization and allocation of resources become increasingly important. In this paper analyzes the current development situation of China’s hydropower. According to the operation characteristics and requirements of cascaded hydropower at different time scales, the paper summarizes the objective functions and constraint conditions in long and short schedule, day-ahead schedule and real-time schedule. As for optimization algorithm, the dimension reduction method of optimal scheduling model is discussed, and the parallel features of dynamic programming algorithm, genetic algorithm and particle swarm algorithm are analyzed. Besides, this paper also introduces the application of parallel computing technology. Finally, the problems that may occur for cascaded hydropower participating in power market and the further research are proposed.

cascaded hydropower station; optimal scheduling; optimization method; parallel computing; power market

10.3969/j.ISSN.1007-2691.2017.05.12

TM721

A

1007-2691(2017)05-0081-10

2017-01-04.

国家自然科学基金资助项目(51277071).

刘方(1989-)，男，博士研究生，主要从事电力优化调度、电力市场等方面的研究；张粒子(1963-)，女，教授，博士生导师，主要从事电力系统经济调度、电力市场和电价理论及应用等领域的教学和科研工作。

doi:10.3969/j.ISSN.1007-2691.2017.05.13