基于无衍射光莫尔条纹的微小位移测量分析

别业广，方照东，吕清花，吕祥，商逸远，黄孝川，万青

(1. 湖北工业大学太阳能高效利用湖北省协同创新中心，湖北 武汉 430068; 2. 湖北工业大学理学院，湖北 武汉 430068)

基于无衍射光莫尔条纹的微小位移测量分析

别业广1,2，方照东1，吕清花1,2，吕祥1，商逸远1,2，黄孝川1，万青1

(1. 湖北工业大学太阳能高效利用湖北省协同创新中心，湖北 武汉 430068; 2. 湖北工业大学理学院，湖北 武汉 430068)

利用He-Ne激光器发出的激光经准直扩束镜后通过轴锥镜，形成径向光强分布呈零阶贝塞尔函数形式的无衍射光，该无衍射光方向性好，在通过反射与折射时不易产生能量损失.然后，通过多次分光与反射得到两束无衍射光，并产生干涉形成莫尔条纹.最后，根据莫尔条纹产生的数目和中心点的位置变化得出位移量，建立莫尔条纹数量变化与微小位移间的数学模型，分析判断工作台产生的偏摆角、滚转角以及俯仰角的误差，并通过ZEMAX软件仿真验证该数学模型的正确性，实现高精度的微小位移测量.

无衍射光；莫尔条纹；ZEMAX软件仿真；微小位移测量

0 引言

目前，很多大型设备需要通过非接触的方式进行微小偏转角度的测量[1-2]，不少学者做过微小角度测量的相关实验.微小角度测控技术在许多领域均有应用，如航空、航天、航海、通信、电子、物理等，如杜佩之等采用动态双光栅测量金属热膨胀系数[3].在国内外有许多运用莫尔条纹进行精密测量的仪器设备，例如武器口径的检测等，均用条形光栅，形成的莫尔条纹可看成是由光栅栅线遮挡所引起的明暗条纹的变化[4-5]，但这种检测方法的结果不够精确，且检测结果不易观察.本文中利用无衍射光的线焦特性并结合莫尔条纹的放大优势，提出基于无衍射光莫尔条纹的微小位移测量技术，采用无衍射光的光强分布模拟圆形光栅，将直角棱镜和半透半反镜组成运动测量单元，固定在光路中，利用探测器对光的吸收成像，结合莫尔条纹的放大特性，实现微小位移的测量，充分利用无衍射光的线焦稳定性.由于运动测量单元的位置与所得到的莫尔条纹的数量和光的中心的位置有对应的数学关系，因此可以直接由莫尔条纹的数目推导得到微小位移量，从而提高系统测量的可靠性.

1 莫尔条纹的基本原理

两束无衍射光产生莫尔条纹的原理图如图1所示，两块光栅在x轴方向的周期分别为d1和d2[5]，其空间频率分别为:

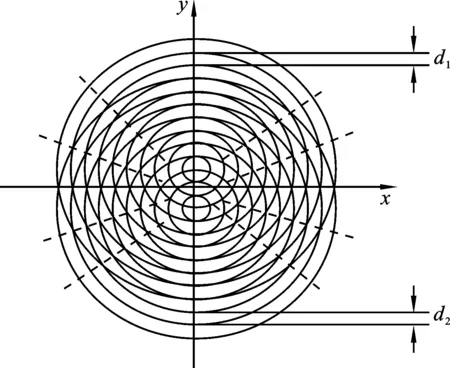
图1 两束无衍射光产生莫尔条纹的原理

(1)

ξ2=1/d2

(2)

其透射率分别为：

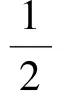
(3)

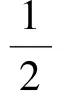
(4)

当用单位强度的光垂直照射两块重叠的光栅时，其透射光的强度函数为:

T(x)=T1(x)T2(x)

(5)

(6)

设圆光栅同心圆的序数分别为m1和m2，半径为x，则有：

x=md

(7)

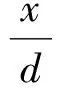
(8)

(9)

其中序数方程：

m1+m2=p

(10)

m1-m2=q

(11)

p为等和条纹，q为等差条纹.

对于同心圆光栅，栅距为a，圆心距为2l，则有：

(x-l)+y2=(m1a)2

(12)

(x+l)+y2=(m2a)2

(13)

带入序数方程(10)式和(11)式可得：

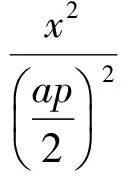
(14)

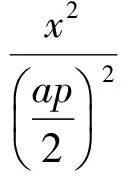
(15)

由(14)～(15)式可知等和条纹方程为椭圆方程，等差条纹方程为双曲线方程，说明在光线干涉加强点的位置形成的亮莫尔条纹为椭圆形，在干涉相消点形成的暗莫尔条纹为双曲线形[5-6]，该结果与仿真得出的实验结果相对应.

2 仿真平台的搭建

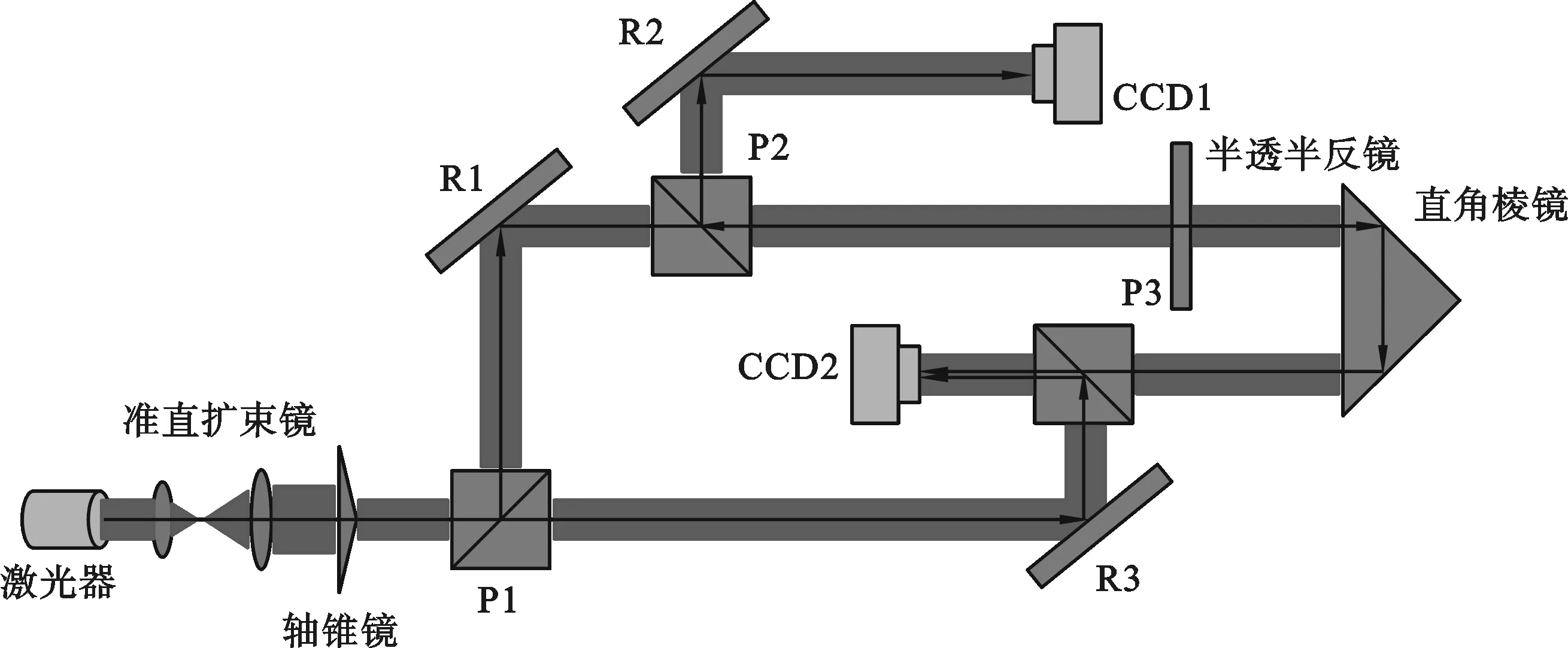
图2 实验光路

如图2所示，He-Ne激光器发出的激光经过准直扩束镜后通过轴锥镜形成无衍射光[6]，经分光棱镜P1后，分成两束无衍射光.光束一部分向上反射，经过反射镜R1入射到分光棱镜P2，经半透半反镜和分光棱镜P2以及反射镜R2被探测器CCD1接收；透过半透半反镜的另一部分光束经过直角棱镜和分光棱镜P3，投射到探测器CCD2上.经分光棱镜P1后的另一束光经过反射镜R3反射后，再经过P3的反射，也投射到探测器CCD2上，两束无衍射光在探测器CCD2上发生干涉. 探测器CCD1上只接收到一束无衍射光，形成一个环形圆光斑[7]，如图3所示；另一个探测器CCD2上接收到两束具有一定光程差的无衍射光，形成干涉莫尔条纹，如图4所示.

通过运用zemax光学仿真软件，搭建对应光路平台，用2 000 000条光线跟踪，观察探测器上的结果，在探测器CCD1上可以看到由单束无衍射光产生的同心圆环条纹(图3)，在探测器CCD2上可以看到由两束具有一定光程差的无衍射光产生的莫尔条纹(图4).

图3 单束无衍射光产生的同心圆环条

图4 两束具有一定光程差的无衍射光产生的莫尔条

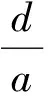
(16)

(17)

θ为莫尔条纹与y轴的夹角，在y轴两侧莫尔条纹对称分布.研究莫尔条纹的变化规律时，取斜率变化角度：0°～90°，可对称地研究其他3个象限的莫尔条纹变化规律[7].

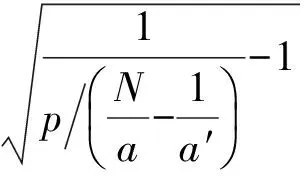
(18)

3 工作台位移与莫尔条纹数目的关系

在zemax仿真软件中，将工作台即棱镜和半透半反镜组成的整体做一个跟随，确保整体移动的距离和偏转的角度一致，减小因移动不相等引起的误差.zemax仿真软件中设置光波长为默认的550 nm，轴锥镜的折射率为1.5，后表面的一次系数为0.000 5，即可产生所需的无衍射光，仿真实验平台的相关参数如表1所示.

表1仿真实验平台参数

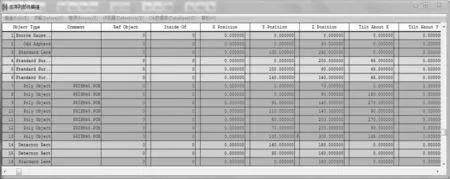
将工作台沿y轴升高或下降0.1 mm记录一次数据，统计相应的莫尔条纹数量，相应的实验结果如表2所示.在观察探测器CCD2时，探测器CCD2上接收到两束相位差恒定的无衍射光，这两束无衍射光发生干涉形成明暗相间的莫尔条纹.设置相应的显示方式为反黑白，取适当的平滑度，当工作台位置对准时，莫尔条纹数目为3条，观察由工作台的位置变化引起的莫尔条纹数目的变化，分析结果可得，工作台沿y轴升高0.1 mm，则多出2条莫尔条纹，对应的中心点的坐标变化0.2 mm.

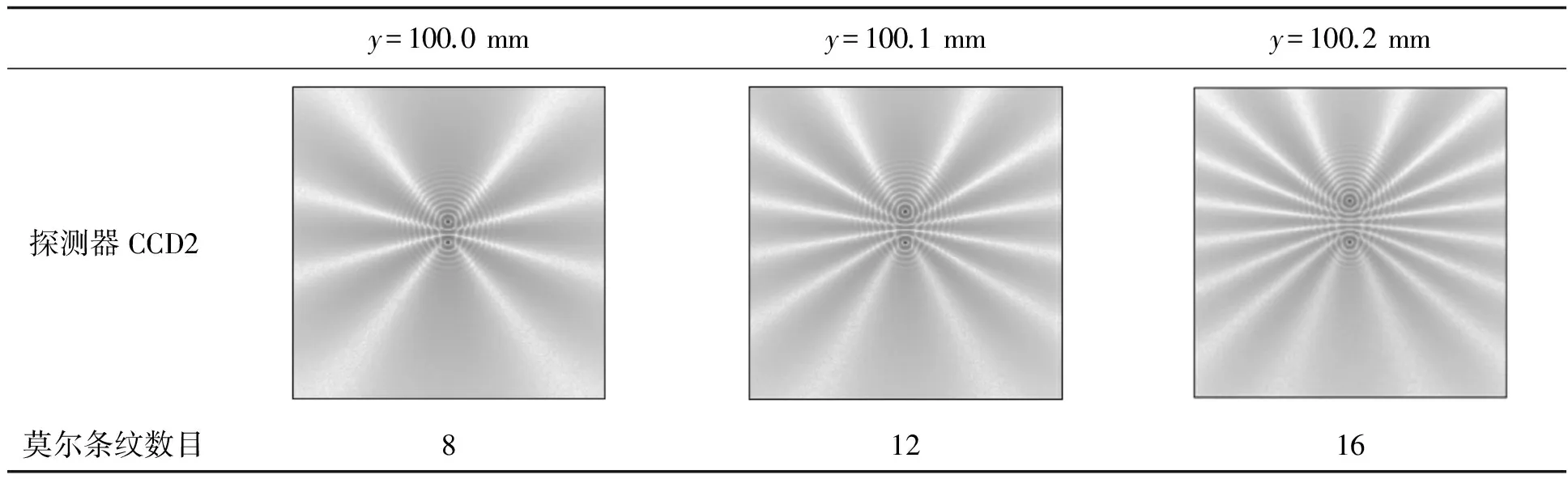
表2 实验数据

由

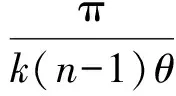
(19)

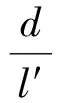
4 工作台绕x、y、z轴偏转与光的中心点位置的关系

工作台分别在x，y，z轴上发生偏转，则分别对应偏摆角、俯仰角和滚转角的变化，相应中心点的位置坐标呈现一定规律的变化，通过几何方法找出其对应的关系后，可直接分析结果，得出工作台的偏摆角、俯仰角和滚转角的误差.

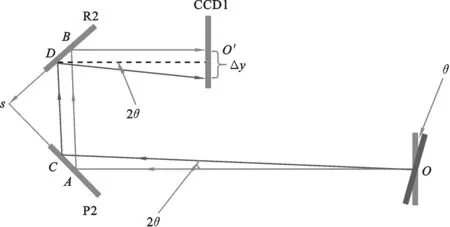
图5 工作台绕x轴偏转时偏摆角变化示意

4.1偏摆角变化如图5所示，工作台绕x轴偏转即偏摆角发生变化，其中O为半透半反镜，P2为分光棱镜，R2为反射镜，CCD1为探测器.当半透半反镜O绕x轴偏转θ角后，探测器CCD1上接收到的光的中心点位置发生改变.偏摆角改变0.1度，则探测器CCD1上得到的同心圆环发生偏移，其中心点的位置发生改变.由相应几何分析及理论推导，可知中心点位置坐标的偏移量与偏摆角之间的关系为线性关系.

假设AB=40 mm，AO=120 m，BO′=40 mm，AC=x1，CS=x2，SD=x3，DB=x4，

(20)

(21)

(22)

(23)

(24)

其中θ角较小，有

sin(θ)≈θ; tan(θ)≈θ

(25)

得Δy=400θ

y≈y0-400θ

(26)

其中θ的单位为rad.由仿真得出的实验结果如表3所示，中心点x坐标变化很小，y坐标与偏摆角的关系基本符合式(26)，与理论推导相符.

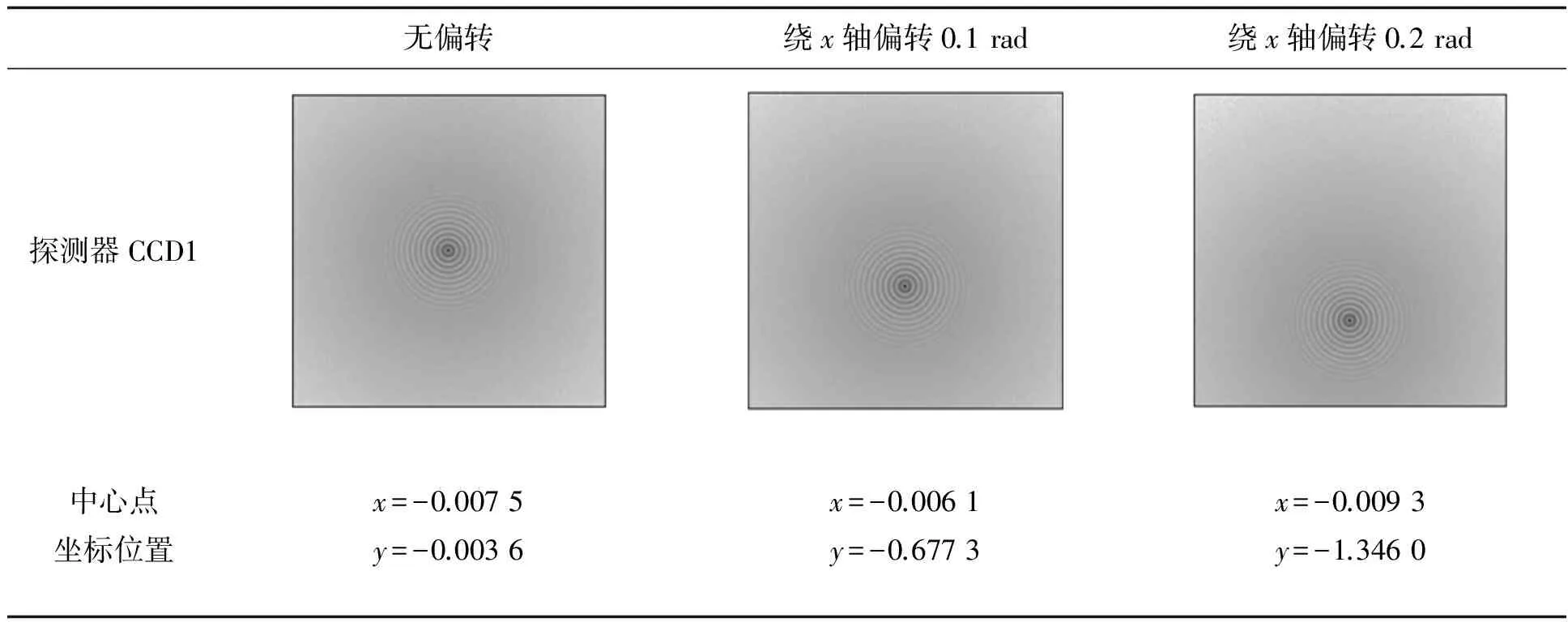
表3 工作台绕x轴偏转引起的光的中心点变化

4.2俯仰角变化当工作台绕y轴偏转即俯仰角发生变化时，产生的误差对仿真实验结果影响较大，光的中心点位置向左移动，不能得到莫尔条纹.但仍可依据扭曲变形的同心圆环干涉条纹，得到光的中心点位置坐标的偏移量与俯仰角的关系.同样可以理论推导得到探测器CCD2上同心圆的中心点位置的x坐标与俯仰角成线性关系：

x≈x0-23θ

(27)

其中θ的单位为rad.由仿真得出的实验结果如表4所示，中心点y坐标变化很小，x坐标与俯仰角的关系基本符合式(27)，与理论推导相符.

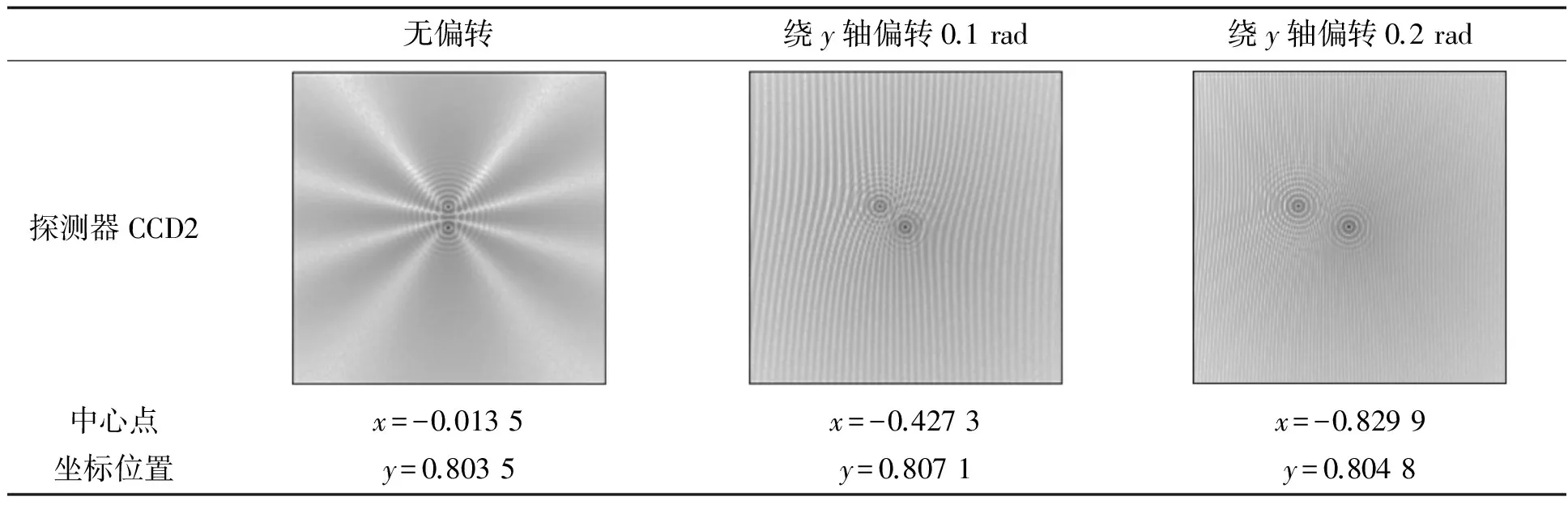
表4 工作台绕y轴偏转引起的光的中心点变化

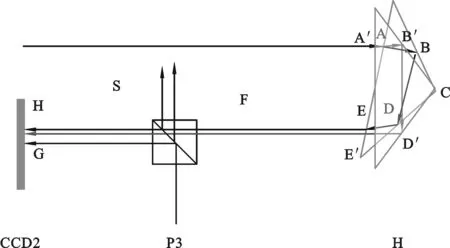
图6 工作台绕z轴偏转时滚转角变化示意图

4.3滚转角变化如图6所示，工作台绕z轴偏转即滚转角发生变化，其中H为直角棱镜，P3为分光棱镜，CCD2为探测器.当直角棱镜H发生微小角度的变化时，经过分光棱镜P3到达探测器CCD2上的光的中心位置发生变化，两束干涉光所形成的条纹发生改变，但仅改变中心条纹的偏转，不改变莫尔条纹的数目.由于工作台绕z轴偏转，在空间中属于二次偏转，在zemax仿真软件中，相应的工作台的位置需要设置成使用x，y，z全局坐标，若没进行此设置，则绕z轴旋转后无法形成莫尔条纹，得到的是无规律的图像.同样可以理论推导得到探测器CCD2上光的中心点位置的x坐标与滚转角成线性关系：

x≈x0+40θ

(28)

其中θ的单位为rad.由仿真得出的实验结果如表5所示，中心点y坐标变化很小，x坐标与滚转角的关系基本符合式(28)，与理论推导相符.

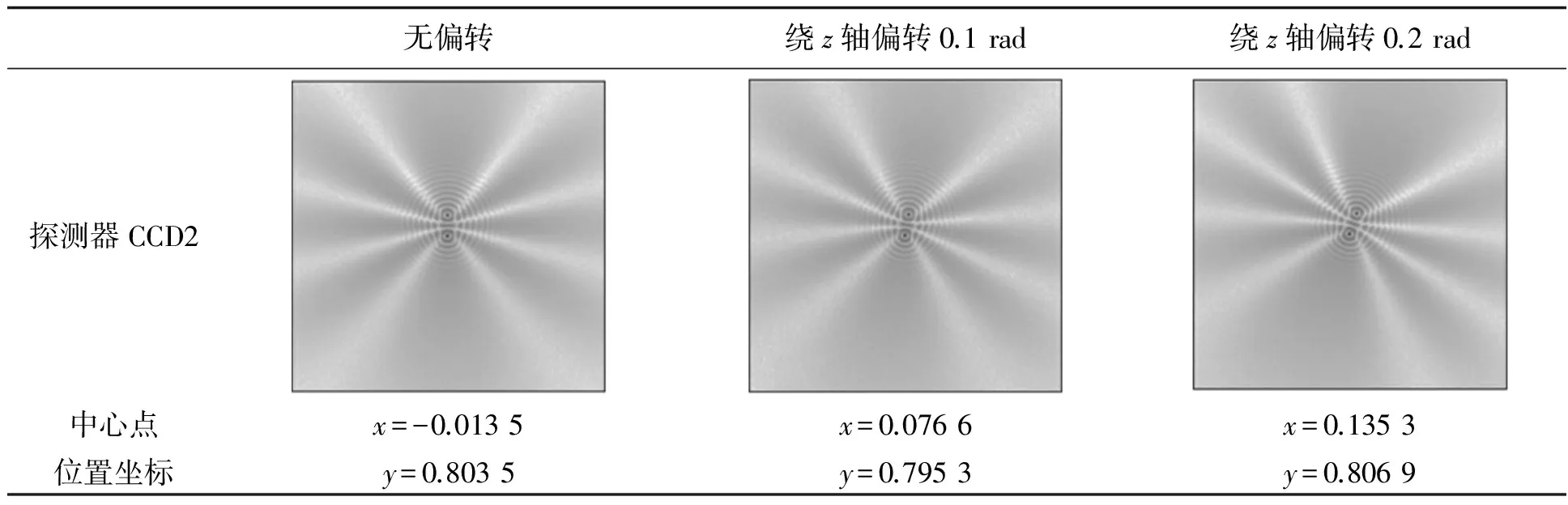
表5 工作台绕z轴偏转引起的光的中心点变化

5 结论

本文中分析莫尔条纹形成的原理，研究莫尔条纹在精确测量运动误差方面的应用，采用无衍射光为分析光束，减少光路中反射和折射的能量损耗，设计的光路简单，涉及的器件少.采用zemax光学模拟软件仿真，得出莫尔条纹数目与运动测量单元的位置之间的对应关系，与理论推导相符.在精密仪器的检测中能更精确反映仪器的实验误差.

[1] 向小燕. 光栅分光式移相干涉差分共焦位移传感技术研究[D]. 哈尔滨：哈尔滨工业大学,2016.

[2] 陆惠宗,屠明亮,纪晨东,等. 激光聚焦偏移测量微小位移方法研究[J].仪器仪表学报,2016(2):461-466.

[3] 杜佩之,高熠鑫,高畅,等.动态双光栅测量金属热膨胀系数[J].物理实验,2013(8):33-36.

[4] 左洋,龙科慧,刘兵,等.非均匀采样光电编码器莫尔条纹信号分析方法[J].电子学报,2015(10):1936-1940.

[5] Wang Ye. Moire Fringe measurement in the data and pixel match of holographic disc storage[C].Optoelectronic Measurement Technology and Applications——Proceedings of SPIE 2008 International Conference on Optical Instruments and Technology,2008, 7160:102.

[6] 郑维涛,吴逢铁,张前安,等.双轴棱锥产生长距离近似无衍射光的新技术[J].物理学报,2012(14):181-187.

[7] Zhai Z, Lv Q, Wang X, et al. Measurement of four-degree-of-freedom error motions based on non-diffracting beam[J]. Optics Communications, 2016, 366:168-173.

Thetinydisplacementmeasurementbasedonthenon-diffractingmoirefringe

BIE Yeguang1,2, FANG Zhaodong1, LV Qinghua1,2, LV Xiang1, SHANG Yiyuan1,2, HUANG Xiaochuan1, WAN Qing1

(1. Hubei Collaborative Innovation Center for High-efficient Utilization of Solar Energy, Hubei University of Technology, Wuhan 430068, China; 2.School of Science, Hubei University of Technology, Wuhan 430068, China)

Using the laser beam emitted by the He-Ne laser is passed through an axicon to generate non-diffracting beam whose radial light distribution is in the form of zero-order Bessel function. Good direction and less energy loss through reflection and refraction are the notable features. Then, two non-diffracting beams are obtained through times of reflection, which will interfere and form moire fringes. Finally, displacement can be calculated using the number of fringes and the position change of beam center. We established the mathematical model between a number of moire fringe change and tiny displacement successfully,and the error of the yaw angle, the roll angle and the pitch angle were analyzed and judged,and then we used ZEMAX software simulation to verify the correctness of the mathematical model, to realize high precision measurement of tiny displacement.

non-diffracting beam;moire fringes;ZEMAX software simulation;the tiny displacement measurement

2017-03-30

国家自然科学基金(51405143,51575164,61475044)、湖北省大学生创新创业项目(20151050023)和湖北省太阳能高效利用开放基金(HBSKFZD2014007)资助

别业广(1964-)，男，副教授；吕清花，通信作者，博士，讲师， Linsa080@126.com

1000-2375(2017)06-0585-06

O436.1

A

10.3969/j.issn.1000-2375.2017.06.005

(责任编辑 郭定和)

收稿日期：2016-12-30

作者简介：张帆(1992-)，男，硕士生；章天金，通信作者，教授，E-mail：zhangtj@hubu.edu.cn

文章编号：1000-2375(2017)06-0597-04