涡轮转子径向变形稳健性优化设计

冯子轩，周 平

（1.中国航空发动机集团有限公司，北京100097；2.北京航空航天大学能源与动力工程学院，北京100083）

涡轮转子径向变形稳健性优化设计

冯子轩1，周 平2

（1.中国航空发动机集团有限公司，北京100097；2.北京航空航天大学能源与动力工程学院，北京100083）

考虑到参数不确定性对转子径向变形的影响，提出了1种基于分布式协同响应面的涡轮转子径向变形稳健性优化方法。首先，利用 K riging模型建立各部件参数与径向变形响应面子模型，然后利用分布式协同响应面方法建立全局参数与转子径向变形的系统响应面模型。其次，利用系统响应面模型建立涡轮转子径向变形稳健性优化模型，并采用果蝇优化算法来进行稳健性优化求解。优化后涡轮转子径向变形的均值以及标准差比优化前分别降低了7.3%和4.97%，计算结果表明：该方法在工程应用中的可行性和有效性。

分布式协同响应面；K riging；涡轮转子；果蝇优化算法；稳健性优化；航空发动机

0 引言

涡轮叶尖径向间隙对航空发动机的性能、安全性都有着非常重要的影响[1]，对其进行精确的设计是研制高性能、高可靠性航空发动机的关键技术[2]。在发动机运转过程中，由于机械载荷和热载荷等诸多因素影响[3-5]，涡轮部件会产生相应的径向变形，因此涡轮结构径向变形准确计算是合理进行叶尖径向间隙设计的基础。目前对于涡轮结构径向变形分析计算的文献大多是基于确定性分析，而对于影响发动机径向变形每个参数在实际中是具有不确定性的，因此考虑参数的随机性对涡轮结构径向变形进行概率分析可以更加合理确定叶尖间隙。学者Fei和Bai[6]通过考虑参数的随机性对涡轮叶尖间隙进行了不确定性分析，通过基于多项式响应面的分布式协同响应面方法进行了叶尖间隙可靠性设计。以上文献分别对涡轮径向变形进行了确定性和不确定性分析计算，提出了各种计算方法精确、高效地估计涡轮结构径向变形。

稳健性优化设计思想是由日本质量专家Taguchi[7]最先提出的，随后稳健性思想被引入工程领域，其中文献[8-9]对稳健性优化做了综述性概括。目前，对于考虑参数不确定性情况下，对设计参数进行稳健性设计来降低涡轮结构径向变形对参数波动的敏感性的方面的研究目前还较为少见。对于不确定性计算而言，需要进行大量抽样统计确定目标响应的分布特性参数，因此对于复杂结构如果直接利用有限元方法进行数千次抽样，其计算时间将十分巨大[6]。

本文提出1种基于分布式协同响应面方法来进行涡轮转子径向变形稳健性优化设计。考虑到涡轮结构参数与径向变形之间非线性关系较强，因此响应面选择Kriging模型[10-11]来拟合参数与径向变形之间的近似函数关系。利用Kriging模型建立涡轮结构各子部件响应面子模型，并进一步建立涡轮转子结构系统响应面模型。最后得到稳健性优化模型，并采用果蝇优化算法对优化模型进行优化求解。

1 基于Kriging模型分布式协同响应面方法

分布式协同响应面方法的基本思路是利用响应面来代替有限元方法进行多对象、多学科协同分析[12]。与传统有限元分析方法相比，基于分布式协同响应面分析方法在保证一定计算精度情况下，可以极大地提高计算效率[6,12]。

首先，建立分布式响应面模型，根据分析对象的结构特点，将复杂机械结构分解为若干子结构，然后分别构造各自的子响应面模型。其次，根据各部件学科之间的耦合特点利用协同响应面方法对子响应面模型进行协同响应分析。这样的一分一合，就能为提高计算精度和计算效率。基于Kriging模型分布式协同响应面发的流程如图1所示。

从图中可见，首先将机械结构分为若干子结构，然后分别对各子结构进行有限元分析计算目标响应，然后通过抽样的方法抽取参数与响应之间的样本点，利用Kriging方法拟合参数与响应之间的函数关系建立子结构响应面模型。最后利用分布式协同计算的方法建立系统总响应面。基于Kriging的分布式协同响应面方法通过建立精确的近似模型替代有限元进行分析计算，从而减少计算时间。

2 涡轮结构模型建立以及参数选取

选取某型发动机1级高压涡轮盘，轮盘材料为GH33。发动机运转情况下涡轮盘前后两侧均有空气冷却。由于主要是针对优化模型及方法的研究，并不是针对涡轮转子径向变形精细化计算，因此为了便于对涡轮盘径向变形分析，对轮盘的榫槽进行简化[6,12]，建立的涡轮盘几何模型如图2（a）所示。涡轮叶片简化叶片的冷却孔及榫头，材料为K419，其有限元模型如图2（b）所示。在计算分析时忽略气动载荷影响[13]，其叶身温度载荷采用函数插值的方式进行加载[14]。

对于影响涡轮盘径向变形参数本文选取涡轮前温度T，转速ε以及相关材料参数作为输入参数，具体参数选取以及数值见表1。

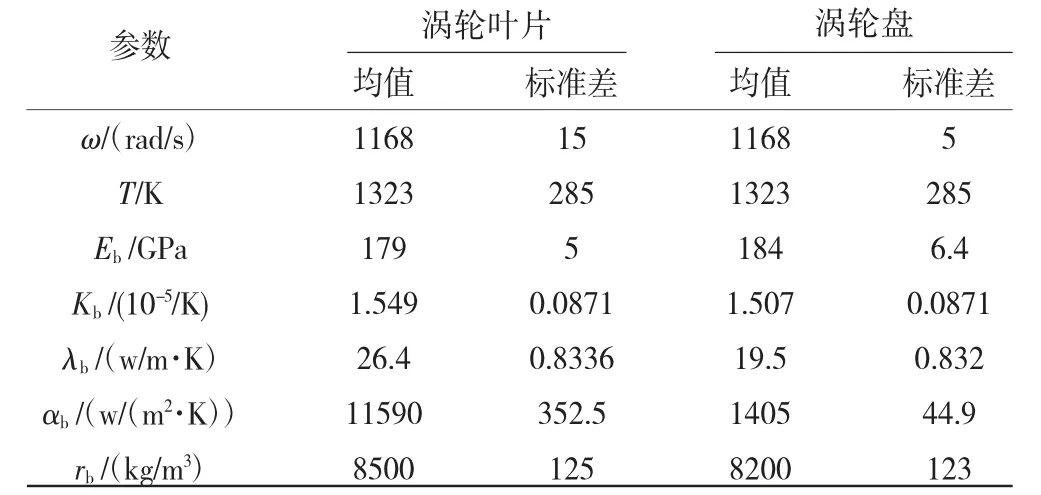
表1 涡轮部件参数均值及标准差

从表1中E和r为材料的弹性模量，K，λ，α分别为热膨胀系数，热导率以及表面换热系数。下标b和d分别代表涡轮盘以及涡轮叶片。

3 涡轮结构子响应面模型建立

对2个部件进行确定性有限元求解后，考虑参数的不确定性，利用拉丁方抽样方法对有限元模型进行150次抽样，其中130组样本用于拟合参数与径向变形Kriging响应面近似模型，20组样本用来验证拟合效果。涡轮盘、涡轮叶片的Kriging近似模型预测效果分别如图3、4所示，其预测值的均方根误差见表2。

表2 涡轮部件Kriging响应面预测值均方根误差

从表中可知，Kriging方法拟合的随机参数与各部件之间的近似函数精度满足工程计算需求。

4 基于分布式协同响应面涡轮结构径向变形稳健性优化

首先，利用分布式协同响应面方法建立涡轮转子参数与径向变形系统响应面模型

式中：F、fi（i=1,2）分别为涡轮结构径向变形总响应面函数、涡轮盘径向变形子响应函数；涡轮叶片径向变形子响应函数x，z为涡轮结构的设计参数以及随机参数向量；xi（i=1，2），zj（j=1，2）分别为涡轮盘、涡轮叶片的设计参数以及随机变量。

根据影响涡轮结构径向变形参数灵敏度分析结果以及参数的特点[15-16]，选取的设计参数见表3，其余的参数为随机参数。从表3中设计参数的优化上限和下限可看出，设计参数设计点的取值范围。

表3 设计参数优化区间

4.1 建立涡轮转子径向变形稳健性优化模型

稳健性优化目的通过寻找合适的设计参数设计点，使涡轮结构径向变形对所有参数变化的敏感性降低，取涡轮结构径向变形标准差为优化目标函数。建立好的稳健性优化模型

式中：xL,xU分别为设计参数的优化区间下限和上限；σ和m为涡轮转子结构径向变形标准差和均值；a为加权系数，对于均值以及标准差的权重要求设定为同一水平，因此a取0.5。

4.2 优化过程和结果分析

采用果蝇优化算[17]法对涡轮转子结构径向变形进行稳健性优化，优化前后的概率密度函数分布如图5所示。优化后的数据结果见表4。

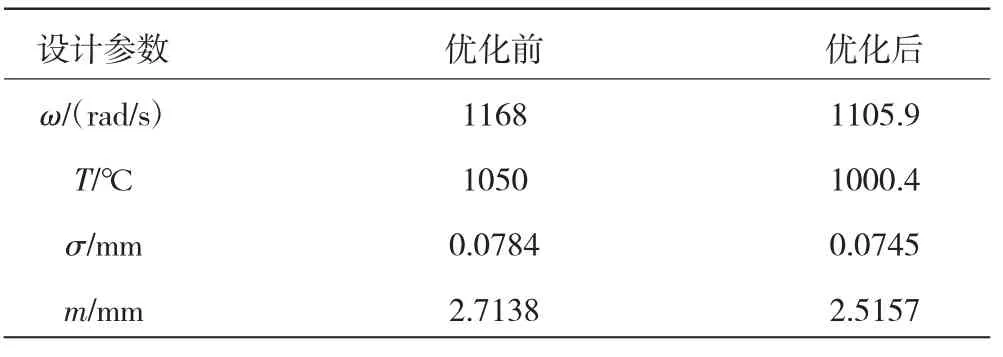
表4 涡轮转子结构径向变形稳健性优化结果

从表中可知，优化后的径向变形均值和标准差比优化前分别减少了7.3%和4.97%，优化结果表明：优化后涡轮结构径向变形对参数的变化敏感性比优化前有所降低，有利于更加合理的进行叶尖径向间隙的设计。

5 结论

提出了1种基于分布式协同响应面方法的涡轮结构径向变形稳健性优化方法，即通过采用Kriging方法建立各个部件响应函数，然后再利用分布式协同响应面方法建立涡轮结构整体径向变形响应面函数。

一方面，利用响应面函数代替有限元法对涡轮结构进行优化分析，可以在保证精度前提下减少优化迭代时间；另一方面，通过对涡轮结构径向变形进行稳健性优化，其径向变形标准差降低了4.97%，也就是说可以更加精确地评估涡轮结构在运转状态下整体径向变形情况，对合理设置径向间隙提供参考。此方法也适用于其他复杂机械结构稳健性优化。

[1]Lattime S B,Steinetz B M.High pressure turbine engine clearance control systems:current practices and future directions [J].Journal of Propulsion and Power,2004,20（2）:302-311.

[2]Hennecke D K，Trappmann K.Turbine tip clearance control in gas turbine engines[R].NASA N-83-229254.

[3]NSSA Glenn Research Center.HTP clearance control [R].NASA CR-2005-213970.

[4]Pilidis P,Maccallum N R L.Models for predicting tip clearance changes in gas turbines[R].NASA N-83-229258.

[5]Annette E N,Christoph W M,Stephan S.Modeling and validation of the thermal effects on gas turbine transients[J].Journal of Engineering for Gas Turbines and Power,2005,127（3）:564-572.

[6]Fei C,Bai G,Tang W.Probabilistic design of HPT blade-tip radial running clearance with distributed collaborative response surface method[J].Journal of Aerospace Engineering,2015,28（2）:1-11.

[7]Taguchi G.Taguchi on robust technology development:bringing quality engineering upstream[M].New York:ASME Press,1994:116-161.

[8]Robinson T J,Borror C M,Myers R H.Robust parameter design:a review[J].Quality and Reliability Engineering International,2004,20（1）:81-101.

[9]Beyer H G,Sendhoff B.Robust optimization-a comprehensive survey[J].Computer Methods in Applied Mechanics and Engineering,2007,196（33）:3190-3218.

[10]Jin R,Du X,Chen W.The use of meta modeling techniques for optimization under uncertainty[J].Structural Multidisciplinary Optimization，2003，25（2）:99-116.

[11]Sakata S,Ashida F,Zako M.Structural optimization using Kriging approximation[J].Computer Methods in Applied Mechanics and Engineering，2003，192（7-8）:923-939.

[12]Bai G C,Fei C W.Distributed collaborative response surface method for mechanical dynamic assembly reliability design[J].Chinese Journal Mechanical Engineering.2013（26）:1160-1168.

[13]Hohlrieder M,Irretier H.Numerical study of the fatigue life of a gas turbine blade in transient operations[R].ASME 94-GT-108.

[14]周平,白广忱.基于神经网络与果蝇优化算法的涡轮叶片低循环疲劳寿命健壮性设计[J].航空动力学报,2013,28（5）:1013-1018.ZHOU Ping,BAI Guangchen.Robust design of turbine-blade low cycle fatigue life based on neural networks and fruit fly optimization algorithm[J].Journal of Aerospace Power,2013,28（5）:1013-1018（in Chinese）

[15]Fei C W,Bai G C.Distributed collaborative probabilistic design for turbine blade-tip radial running clearance using support vector machine of regression[J].Mechanical Systems and Signal Processing,2014,49（1）:196-208.

[16]Pan W T．A new fruit fly optimization algorithm:taking the financial distress model as an example[J].Knowledge based Systems,2012,26（2）:69-74.

Robustness Optimization Design of Radial Deformation for Turbine Rotor

FENG Zi-xuan1,ZHOU Ping2
（1.Aero Engine Corporation of China,Beijing100097,China;2.School of Energy and Power Engineering,Beihang University,Beijing 100083,China）

Considering the influence of parameter uncertainty on the rotor radial deformation,the turbine rotor radial deformation robustness optimization method was put forward based on distributed coordinated response.Firstly,the Kriging model was used to build the surface model of the component parameters and the radial deformation response model.Then,the response surface model of the global parameter and the rotor radial deformation was established by using the distributed cooperative response surface method.Secondly,the optimization model of radial rotor stability of turbine rotor was established by using the system response surface model,and the fruit flies optimization algorithm was used to solve the robustness optimization.The optimization results show that the mean value of the radial deformation of the turbine rotor and the standard deviation ratio are reduced by 7.3%and 4.97%before optimization.The results show that the method is feasible and effective in engineering application.

distributed collaborative response surface;Kriging;turbine rotor;fruit flies optimization algorithm;robustness optimization；aeroengine

V 232.3

A

10.13477/j.cnki.aeroengine.2017.05.006

2017-06-16

冯子轩（1985），男，硕士，工程师，从事科研管理、重点实验室管理等工作；E-mail:376548551@qq.com。

冯子轩,周平.涡轮转子径向变形稳健性优化设计[J].航空发动机，2017，43（5）：31-34.FENG Zixuan,ZHOU Ping.Robustness optimization design of radial deformation for turbine rotor[J].Aeroengine，2017，43（5）：31-34.

（编辑：张宝玲）