基于三相量实现正弦信号非同步采样的精确频率测量
严结实 王文静
基于三相量实现正弦信号非同步采样的精确频率测量
严结实1王文静2
(1. 西安西电自动化控制系统有限责任公司,西安 710043;2. 西电通用电气自动化有限公司,西安 710018)
在电能质量监测和继电保护装置研制中,精确频率测量是所有电参数精确测量的前提和基础。对有限频偏的正弦信号,为实现非同步采样条件下精确频率测量,应用相量理论。本文首先提出三相量测量原理,给出理论推导和仿真验证;其次引用DFT变换,用各序列的实部、虚部进行推导计算,同样实现非同步采样情况下的精确频率测量。对比仿真验证结果表明,两种方法仿真结果完全一致,印证了基于三相量实现非同步采样精确测频方法的正确性。此结论为电力测量装置、保护装置的研发提供了一条非常有意义的精确测频方法。
相量;非同步采样;DFT;频率测量
在电能质量监测和继电保护装置研制中,保持对交流电信号的同步采样是准确获得基础数据的前提和必要条件,但实际的电网频率会在基频点上产生一定的偏差或摆动。在信号离散化时,多数情况下是按基频的整倍数进行采样,以此数据进行电参数计算,但会因非同步采样产生功率泄漏和栅栏效应[1],造成一定的误差,有些误差可以被允许,有些误差会导致测量或保护的误判,甚至造成事故。因此,当今数字化装置首先要精确测量的物理量就是交流电信号的频率,以此精准频率为参考实现同步采样,经DFT求解相关电参数,如电流、电压、相位、功率等,以及进行电能质量分析和保护算法的计算。
对频率的测量有许多途径和方法,如纯硬件(含FPGA)测周测频法[2]、经DFT变化的单峰值插值法[3-4]或双峰值插值法[5]、DFT变换中修正相角差测频法[6]、DFT变换中修正正弦因子迭代法[7]、DFT变换中相量修正测频法[8]、修正时域序列的DFT变换法[9-11],其他方法[12-15]等,各种方法仿真都能实现较准确测频,测量误差小于指定误差,满足工程应用需求,但有一点是相同的,即都是基于非同步采样下的DFT,且在实际测频计算中,均采用了近似或逼近的计算方法。经过研究分析,本文提出了基于三相量实现非同步采样的精确测频,并且假定在构建向量采样的时间区间内,频偏保持不变,即当=50Hz+D时,D为常数,理论计算可以做到无误差测频。
1 三相量实现精确频率原理
设被测信号为单频正弦信号,其指数形式表示为
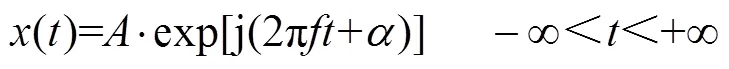
式中,为幅值;为初相;为信号频率;待测。它会在基频点50Hz附近,产生一定范围的相对缓变的频偏,例如D≤±5Hz。对此信号以间隔为s进行等间隔采样,s为采样周期,设0为理想基频,例如0=50Hz,单周期采样点,取采样频率s= 1/s=·0,因为对测量频率,一般s≠·,所以此采样属于等间隔非同步采样,对()进行离散化,其序列为(),表示如下:

对离散序列(),分别右移1个s点和2个s点,构建两个新序列1()、2(),表示如下:
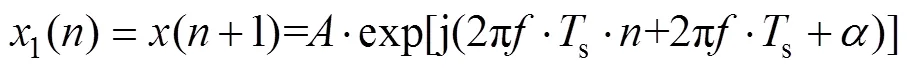
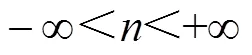



以式(5)做相量图,用代表()、用代表1()、用代表2()。还假设在构建离散序列()的两个周期时间内,频偏保持不变,即=50Hz+D,D在两个周期采样时间内保持不变,这个假设符合实际电网运行情况,即在两个周期时间内认为电网频率保持不变,这样,所构建的3个相量的特点就是幅值相等,两两间相角差恒定,如图1所示。
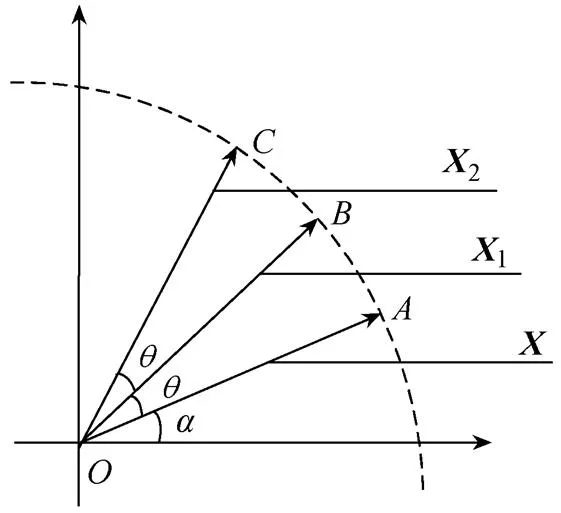
图1 三相量图
在图1中,依据相量合成法则,求相量与相量之和,即+,其交点位于的延长线上,虚线表示,连接交于点,则四边形为等边菱形,如图2所示。
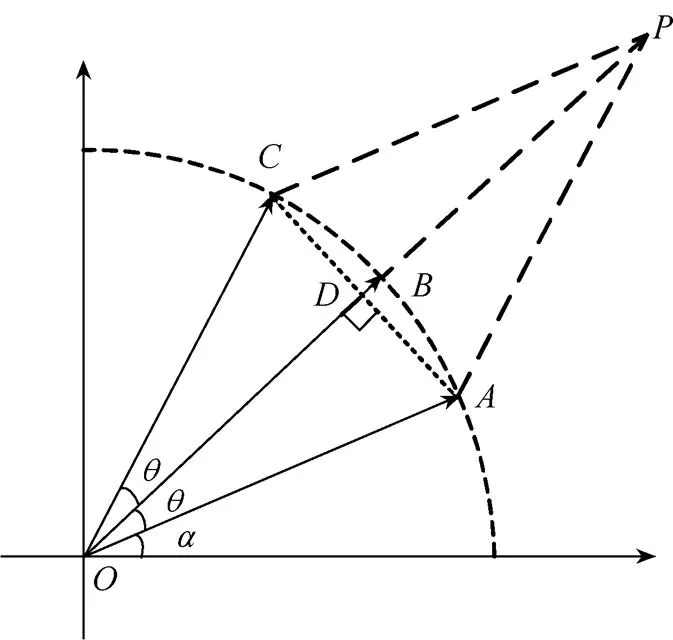
图2 相量合成图
则有
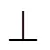
与为同方向相量,D≌D
又∵ ||=||·cos
||=||两相量幅值相等
与为同方向相量
∴=·cos
由式(6)可知,对于按式(2)、式(3)、式(4)构建采样序列,以相量表示,相量与相量之和的一半和相量为同方向相量,二者的比值必为标量,其大小为相量夹角的余弦值。参考式(5),可以用1、2三相量代入式(6)得式(7),这样将采样序列()、1()、2()与被测频率建立起直接函数表达,令


由式(7)、式(9)知,只要知道3个采样序列,就可以准确地计算出待测频率,s为采样频率属已知量。当然信号采样应满足采样定理,进行等间隔采样,对是否满足同步采样不做要求,这点对实际应用很有意义。
从上述论证中可以得到如下结论。
1)设定被测正弦信号含有缓变频偏,即=0+D,0为理论基频,对信号按s=·0进行均匀采样,一般s≠·,不满足同步采样,所以,这样的采样为均匀非同步采样。
2)再设定在+2个采样时间内,D保持恒定,以此来构建()、1()、2()采样序列,应用式(8)、式(9)可以求得所在+2采样时间段的精确频率。
3)按此思路,对+2之后每来一个采样点,就能构建3个新的采样序列()、1()、2(),就能精确测量频率一次,所以除第一次需要(2)s时间外,随后每来一个采样点都能精确测频一次。
4)此方法最大特点是,将采样序列与待测频率建立起直接运算关系,如式(8)、式(9),其次是频偏大小不影响频率测量精度。这为快速精确计算电网频率提供一种很好的途径。
2 实例仿真验证
设待测信号为
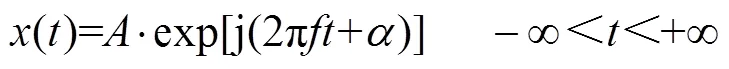
式中,=10,=p/6,=45.00~54.99Hz,理论基频0=50Hz,采样频率为s=·0(Hz),为每周波采样点数,取=64,参考式(2)、式(3)、式(4),构建3个采样序列()、1()、2(),取主周期序列表示如下:

通过Matlab[10]进行仿真,不失一般性,频点随机设置,仿真结果见表1。
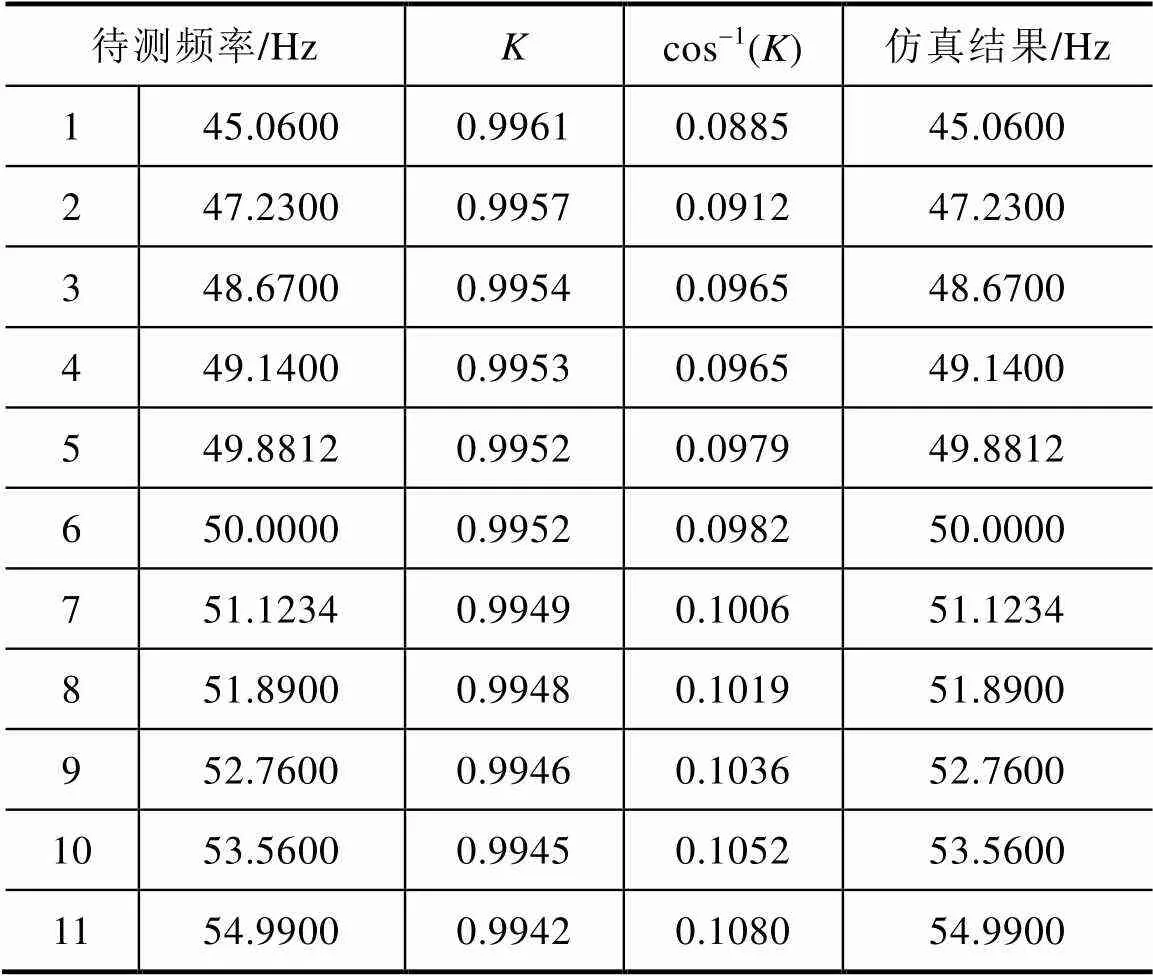
表1 三相量频率测量仿真结果
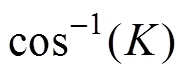
从仿真结果说明,以基频点为中心,给定一定范围内一定精度的任意频率,通过构建3个相量可准确地求解出被测频率,此结论为电力测量装置、保护装置的研发奠定了一条非常有意义的精确频率测量的快速途径。

表2 高精度显示仿真结果
但是,依据式(8)、式(9)的求解,因两种运算会给实际应用带来较大工作量,影响到装置的实时性、或者因需要高性能处理芯片增加成本,这两种运算一是相量相除(因较大),二是求反余弦。对求反余弦函数,在一定精度范围内,应用泰勒级数也可以近似求解求反余弦函数,参看第4节;对相量相除或求逆运算,因=64,运算量较大,能否换一种思路,将获得的采样序列()、1()、2()经DFT变换转化成对应的实部、虚部,再应用式(8)、式(9)求解。
3 基于DFT求解测频计算
参考三相量表达式(5)和三相量图1,对离散信号()、1()、2(),取其主周期序列分别进行基波频率的DFT变换,则



对等间隔同步采样,式(12)、式(13)、式(14)表示如下:
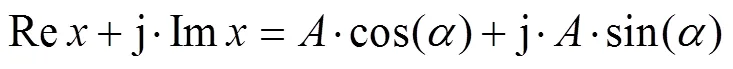

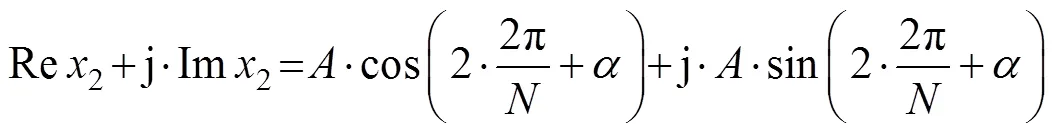

则式(8)可写成

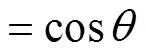
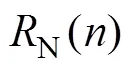



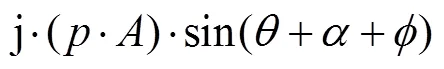
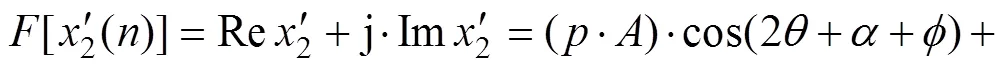

代入式(8)得


此时,令

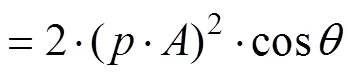
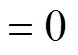
将、代入上式得
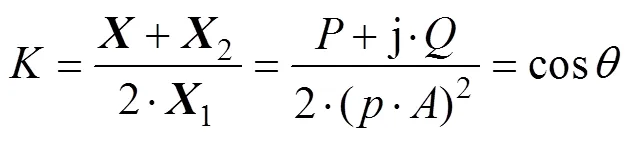
从上述证明中,可以得到:①对带有频偏的正弦信号,只要均匀采样,不管是否同步,按式(2)、式(3)、式(4)要求所构建采样序列,取其DFT变换的实部、虚部,代入式(8)求比值,其值恒为一常量;②其比值的大小等于相量旋转角的余弦值,且此值不受是否同步采样的影响,只要满足均匀采样即可,这点为工程应用奠定了理论基础;③用式(9)即可准确求得信号频率,此结果与相量计算结果相同,从理论上得到相互印证。所以,此方法先求三序列的DFT,并令

在求得值后,应用式(9)即可求得待测频率。这样式(9)、式(27)将是工程化应用的准确计算频率的核心公式。那么这两种仿真计算的结果一致吗?取表1的部分数据重做仿真,仿真结果见表3,结果是两者完全相同。

表3 基于DFT的三相量仿真结果
此仿真结果进一步说明,对于非同步采样构建三相量应用DFT求比值实现精确测频方法的正确性。
4 小频偏条件下的反余弦近似求解


(0>>D) (28)
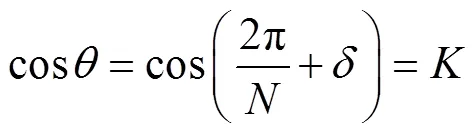
对测量频率分辨率小于0.1Hz的,采用一阶泰勒级数展开,即

对测量频率分辨率小于0.01Hz的,采用二阶泰勒级数展开,即
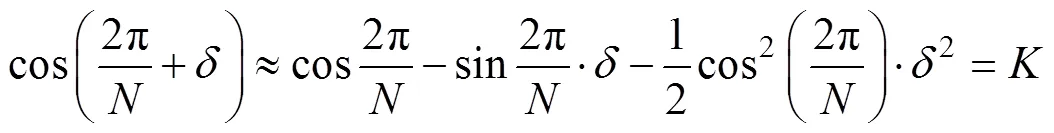
一旦解算出,则待测频率为

对式(30)、式(31)、式(32)验证较为简单,在此不做阐述。
5 结论
本文从相量分析的角度,提出了构建三相量序列实现非同步采样情况下精确频率测量,应用Matlab给出了各种高精度频偏的仿真验证,其结果与理论分析完全一致;其次引用非同步采样条件下的DFT变换,用各自序列的实部、虚部进行推导和计算,同样实现了非同步采样情况下精确频率测量,此结论为电力设备智能化研制中的测频技术提供了非常有价值的解决方案,也为精准计算电参数奠定了可借鉴的理论基础;本文最后结合实际工程应用,提出了应用泰勒级数近似求解反余弦函数的快速方法,也具有一定的实用意义。
[1] 张伏生, 耿中行, 葛耀中. 电力系统谐波分析的高精FFT算法[J]. 中国机电工程学报, 1999, 19(3): 63-66.
[2] 周卫平, 吴正国, 夏立. 基波相位和频率的高精度检测及在有源电力滤波器中的应用[J]. 中国电机工程学报, 2004, 24(4): 91-96.
[3] 王茂海, 孙元章. 基于DFT的电力系统相量及功率测量新算法[J]. 电力系统自动化, 2005, 29(2): 20-24.
[4] 侯启方, 李艳鹏, 刘承志. 基于插值FFT算法的电力系统频率高精度测量[J]. 电气应用, 2007, 26(6): 99-102.
[5] 庞浩, 李东霞, 俎云霄, 等. 应用FFT进行电力系统谐波分析的改进算法[J]. 中国电机工程学报, 2003, 23(6): 50-54.
[6] 吴梓亮, 李银红, 李明, 等. 一种基于修正相角差的傅氏测频算法[J]. 电力系统保护与控制, 2015, 43(13): 111-117.
[7] 牟龙华, 邢锦磊. 基于傅立叶变换的精确频率测量算法[J]. 电力系统自动化, 2008, 32(23): 67-70.
[8] 谢运华, 赵庆生, 郭贺宏, 等. 基于高精度测频的修正DFT相量及功率测量算法[J]. 电力系统保护与控制, 2016, 44(12): 23-28.
[9] 唐建辉, 胡敏强, 吴在军. 一种基于修正采样序列的电力系统频率测量方法[J]. 电力系统及自动化学报, 2004, 16(6): 52-54.
[10] 吴天明, 谢小竹, 彭彬. MATLAB电力系统设计与分析[M]. 北京: 国防工业出版社, 2004.
[11] 程佩青. 数字信号处理教程[M]. 4版. 北京: 清华大学出版社, 2013.
[12] 杜佳玮, 杨鹏, 史旺旺. 考虑频率变化的基于DFT单相数字锁相环的椭圆拟合方法[J]. 电力系统保护与控制, 2015, 43(10): 85-90.
[13] 朱何荣, 王敏, 孙颂林, 等. 高次谐波对测控装置测量影响解决方案设计与实现[J]. 电气技术, 2016, 17(10): 53-58.
[14] 程诗明, 郭明宇, 贺儒飞, 等. 基于实测信号的抽水蓄能机组频率自适应算法研究[J]. 电气技术, 2017, 18(4): 106-109.
[15] 吴振杰, 符光辉, 吴靖. 三相软件锁相环在便携式IEC 61850测试装置中的应用[J]. 电气技术, 2015, 16(10): 84-87.
Nonsynchronous Sampling Precise Frequency Measurement for Sine Signal based on Three-phase Sequence
Yan Jieshi1Wang Wenjing2
(1. Xi’an XD Automated Control System Co., Ltd, Xi’an 710043;2. XD-GE Automation Co., Ltd, Xi’an 710018)
The development of power quality monitoring and relay protection device,precise frequency measurement is the prerequisite and basis for accurate measurement of all electrical parameters. The thesis uses sequence theory to realizeprecise frequency measurement at nonsynchronous sampling condition for limited frequency deviation sine signal. Firstly, elucidated three-phase sequence measurement theory, gave theoretical derivation and simulation verification. Secondly, used DFT transform, calculated with real and imaginary parts of the three-phase sequence, also completedprecise frequency measurement at nonsynchronous sampling condition. Compared the simulation and verification. The two simulation resultsare the same. This conclusion shows that nonsynchronous samplingbase on three-phase sequence for precise frequency measurement is right. This conclusion provides a very meaningful method of precise frequency measurement for the research and development of electric power measuring device and protection device.
phase sequence; nonsynchronous sampling; DFT; frequency measurement
严结实(1963-),男,硕士研究生,高级工程师,主要从事电力控制与保护方面的研究和技术管理工作。
陕西省重大科技创新专项(2016ZKC01-20)

