光伏发电MPPT的模糊逻辑控制及仿真

郭海霞

(山西农业大学 工学院，山西 太谷 030801)

光伏发电MPPT的模糊逻辑控制及仿真

郭海霞

(山西农业大学 工学院，山西 太谷 030801)

[目的]为提高光伏发电效率，使光伏电池迅速工作在最大功率点。[方法]本文结合光伏电池的等效模型，分析其输出特性，采用模糊逻辑控制方法对光伏电池最大功率点进行跟踪控制，基于Matlab/Simulink建立光伏电池最大功率点跟踪的模糊控制仿真模型。[结果]仿真结果显示模糊逻辑控制法能瞬间实现光伏电池最大功率点跟踪。[结论]模糊逻辑控制法能显著改善最大功率点振荡，使系统有良好的稳态和动态性能。

最大功率点跟踪； 模糊控制； 光伏电池； 仿真

随着全球经济和商业的快速发展，能源供求出现失衡，能源资源紧张问题日益凸现[1,2]。太阳能以其资源丰富、分布广泛等优点，已成为一种重要的可再生能量[3]。太阳能的主要应用之一是光伏发电，光伏发电有着广阔的发展前景，备受人们关注[4]。但光伏电池本身与环境温度、光照强度及负载等因素存在明显的非线性关系，导致其转换效率低，不能稳定工作在最大功率点上，造成了能源浪费[5]。为了提高光伏发电的输出效率，使其在同等条件下输出更多的电能，需对其输出的最大功率点实现跟踪控制[6]。目前常用的光伏电池MPPT(Maximum Power Point Tracking)控制方法有电导增量法[7]、恒定电压法[8]和扰动观察法[9,10]等，采用上述方法对最大功率点跟踪控制时，跟踪效果不理想、代价高、实现困难，而且复杂程度高。

模糊控制是一种自寻最优的非线性智能控制[11]方式，其数学模型简单，灵活性好，适应性强。本文通过模糊逻辑控制法实现光伏电池的最大功率点跟踪，在Matlab/Simulink环境下建立光伏发电的MPPT控制仿真模型，并将仿真结果与传统的扰动观察法进行对比与分析。

1 光伏电池等效模型与特性

光伏电池常用的实际等效电路[12]如图1所示。

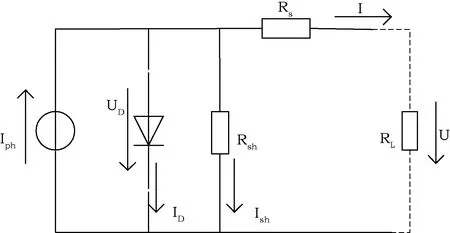
图1 光伏电池等效图Fig.1 Equivalent circuit of photovoltaic cell

图1中，Iph为光生电流/A；ID为流入二极管的电流/A；I为光伏电池输出的电流/A；UD为二极管的端电压/V；U为负载端电压/V；RL为电池的负载电阻/Ω；Rs和Rsh分别为等效串、并联电阻/Ω。

光伏电池的输出I-U特性如式(1)所示。

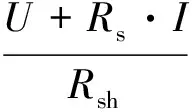
(1)

式(1)中，I0是图1中D的PN结反向饱和电流/A；q是电荷量，值为1.6×10-19/C；k是波尔兹曼常数，值为1.38×10-23/J·K-1；T是绝对温度/K。

在温度25 ℃、光照强度1 000、800、600 W·m-2三种情况下光伏电池的输出特性P-U曲线和I-U曲线分别如图2和图3所示。

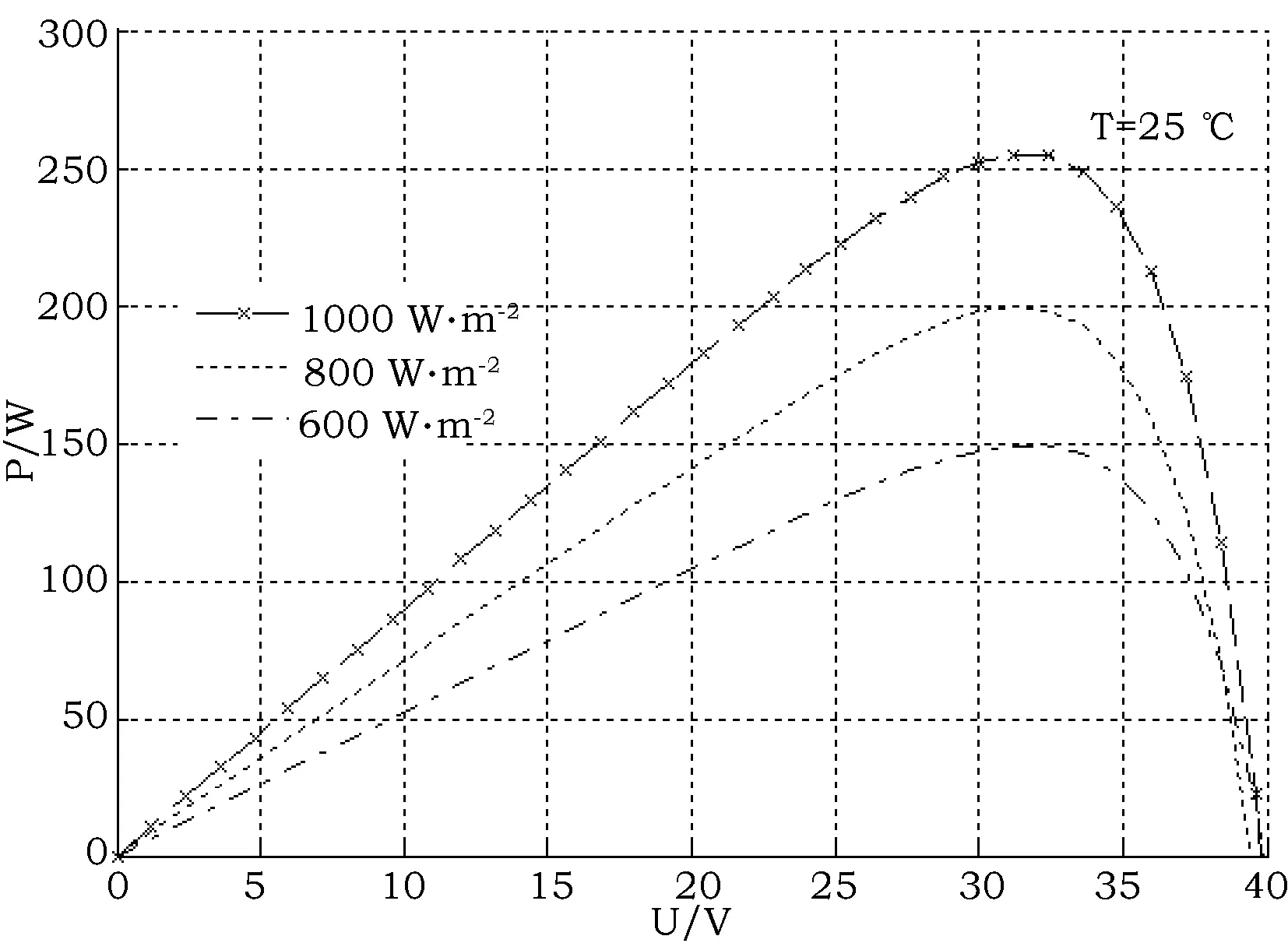
图2 不同光照下的P-U曲电压Fig.2 P-U curve under different lights

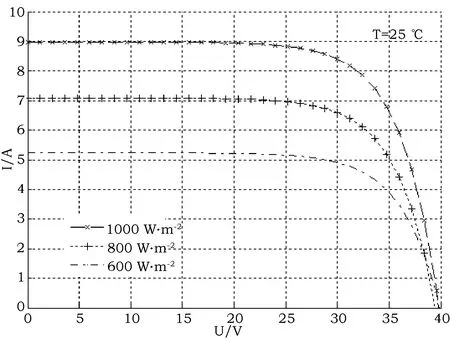
图3 不同光照下的I-U曲线Fig.3 I-U curve under different lights

由图2可知，保持温度不变，光伏电池的输出功率特性受光照强度影响很大，随着光照强度的增大，最大功率也增大。

由图3可知，光伏电池输出的短路电流随光照强度的增大而增大，且在MPP左侧部分重负荷下，光伏电池类似于恒流源，在MPP右侧部分轻负荷下类似于恒压源。

在光照强度1 000 W·m-2、温度25、50、75 ℃三种情况下光伏电池的P-U曲线和I-U曲线分别如图4和图5所示。

图4 不同温度下的P-U曲线Fig.4 P-U curve under different temperatures

图5 不同温度下的I-U曲线Fig.5 I-U curve under different temperatures

由图4可知，保持光照强度不变，光伏电池的最大功率随温度的升高而逐渐降低。

由图5可知，保持光照强度不变，光伏电池输出的短路电流随温度的升高而不断增大。

由以上分析可知，光伏电池是一种非线性电源，其输出最大功率点与输出电流会随着光照强度和所处环境温度的变化而发生移动，因此需要通过MPPT控制措施使光伏电池的输出功率在最大功率点稳定。

2 MPPT模糊控制实现

模糊逻辑控制是一种人工智能控制。MPPT模糊逻辑控制基于光伏电池的非线性输出特性提出。为实现MPPT控制，模糊控制系统将采样电压和电流进行计算得出功率，然后判断出工作点与最大功率点之间的位置关系，自动调整工作点的输出电压，使系统在接近最大功率点工作[13]。

模糊控制的实现需要经过模糊化、模糊规则和模糊判决三个环节[14]。模糊控制系统基本原理如图6所示。

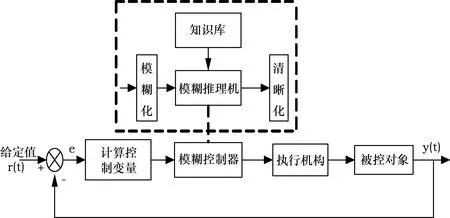
图6 模糊控制基本原理图Fig.6 Basic principle diagram of fuzzy control

2.1 模糊化

模糊逻辑控制器的输入通常为误差E和误差变化量ΔE，此结构反映模糊逻辑控制器具有非线性PD(Proportion Differentiation)控制规律，可有效保证系统的稳定性，并减少相应过程的超调量以及消弱振荡现象[15]。在光伏发电MPPT控制中，当dP/dU=0时，光伏系统对应的工作点为最大功率点。实时检测光伏系统输出电压和输出功率的数据，用n和n-1分别表示当前采样数据和上次采样数据[15]。本文采用单变量二维模糊控制器[16](二维输入、一维输出)设计模糊逻辑控制器，即将E(n)和ΔE(n)作为模糊控制器的输入量，将PWM(Pulse Width Modulation)占空比D的变化量ΔD(n)作为模糊控制器的输出量。将模糊控制器输入量E与ΔE分别定义如式(2)～式(4)：

E(n)=[P(n)-P(n-1)]/[U(n)-U(n-1)]

(2)

ΔE(n)=E(n)-E(n-1)

(3)

ΔD(n)=D(n)-D(n-1)

(4)

其中，P(n)、U(n)分别为第n次采集到的光伏电池输出功率和输出电压；D(n)为第n次采集时的PWM占空比。当满足E(n)=0时，光伏电池此刻的输出功率为最大功率[14]。

定义模糊集合E、ΔE和ΔD分别为5个模糊子集，即：

E={NB,NS,ZO,PS,PB}，对应的论域为{-0.08，-0.06，-0.04，-0.02，0，0.02，0.04}；

ΔE={NB,NS,ZO,PS,PB}，对应的论域为{-200，-150，-100，-50，0，50，100，150，200}；

ΔD={NB,NS,ZO,PS,PB}，对应的论域为{-0.04，-0.03，-0.02，-0.01，0，0.01， 0.02，0.03，0.04}；

定义中的NB，NS，ZO，PS，PB分别表示负大，负小，正零，正小，正大。根据光伏电池特征，隶属度函数形状选择三角形状。

2.2 确定模糊控制规则

分析光伏电池的P-D特性曲线，若检测到当前正向调整PWM的占空比D使输出功率增加，则继续向正方向原步长调控[17]；若检测到功率减小，则改为反方向调控；若检测到工作点距离最大功率点较远时，则采用较大步长使跟踪速度变快；若检测到工作点在最大功率点附近，则采用较小步长，以减少搜索带来的功率损失；当环境温度、光照强度变化使光伏电池输出功率变化较大时，系统能快速作出反应。根据上述控制原则，得出模糊控制规则如表1所示。表1显示输出变量ΔD随输入误差E和误差变化量ΔE的变化规则，控制规则的目的是使变量E恒为0。

2.3 模糊判决

由于最终需要的是一个精确控制量，而模糊推理得到的是一个模糊集合或隶属函数，因此需要将此模糊量转化成执行机构可以接受的精确量[18]，这个转换精确量可以直接去控制被控对象。将模糊集转换成精确值的过程一般称为模糊判决过程，也称解模糊或者清晰化。常用的解模糊化方法有平均最大隶属度法、中位数法、求和法、估值法、面积重心法和面积平均法等。面积平均法的计算公式如式(5)所示。

表1 模糊控制ΔD规则表Table 1 Rule table of fuzzy control ΔD

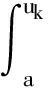
(5)

式(5)中，uk为隶属函数曲线u(k)与横坐标包围区域的面积平分线对应的横坐标，uk∈[a,c]。由于本文隶属函数的面积选为三角形，所以求出面积的一半所对应元素的位置即可，计算方法简便合理。

3 建模及仿真分析

基于Matlab/Simulink建立光伏电池仿真模型如图7所示。

图7中，标准参考温度25 ℃，标准参考光照强度1 000 W·m-2，最大功率点电压21.7 V，最大功率点电流4.5 A，开路电压24.2 V，短路电流4.8 A，电压温度系数0.77 V·℃-1，电流温度系数0.02 A·℃-1。

对图7光伏电池仿真图进行封装，根据模糊控制原理建立光伏发电MPPT的模糊控制仿真模型如图8所示。

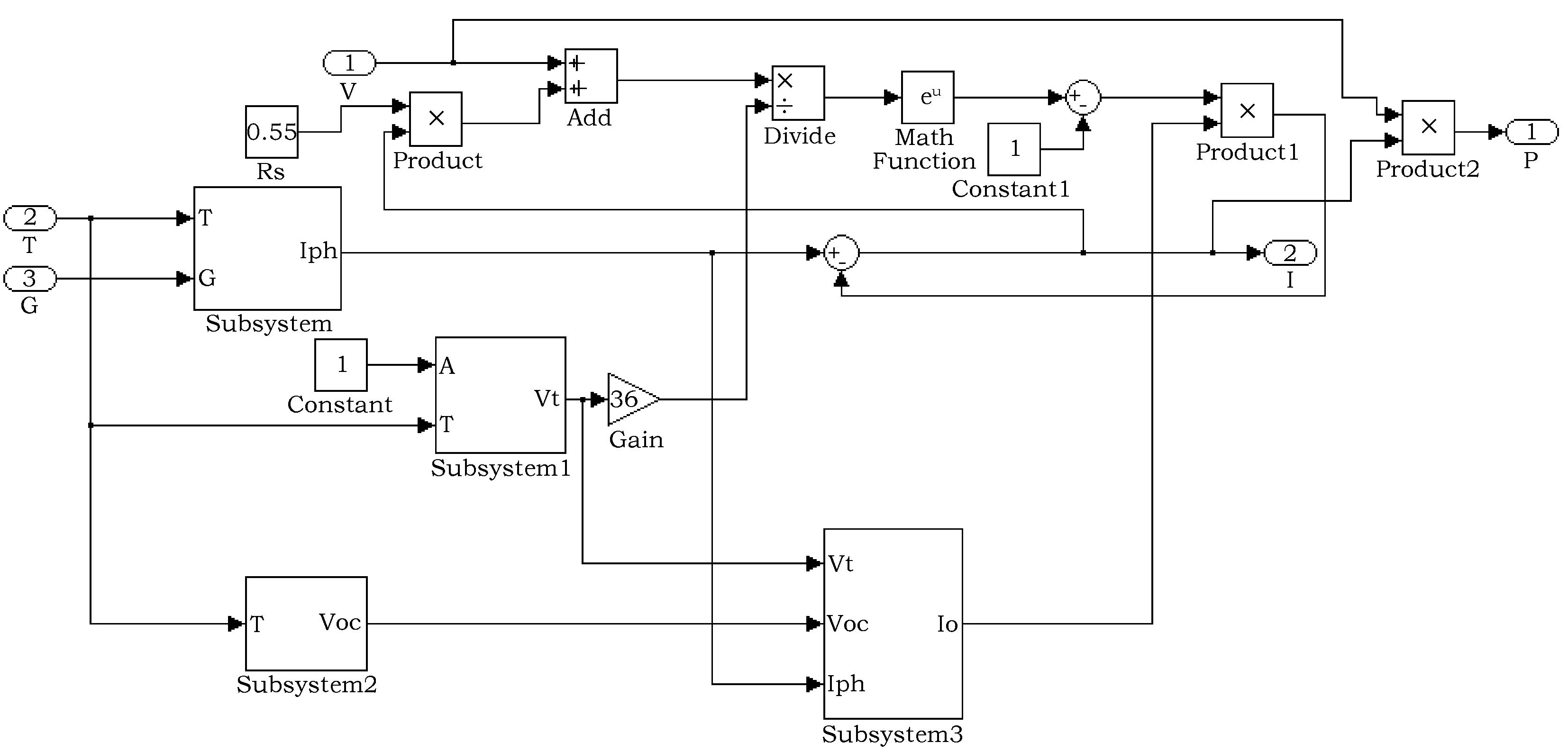
图7 光伏电池仿真模型图Fig.7 Simulation model for PV cell

光伏发电模型初始工作在温度25 ℃，光照强度1 000 W·m-2的条件下，保持温度不变，在t=0.5 s时，光照强度由1 000 W·m-2突变为600 W·m-2时，模糊控制法光伏电池的输出功率及输出电流跟踪图如图9和图10所示。

由图9和图10可知，模糊控制法在环境突变时几乎无波动，且能迅速达到最大功率点，其跟踪速度快。

图11和图12为与模糊控制法同等参考条件下，扰动观察法输出功率和输出电流跟踪图。

由图11和图12可知，扰动观察法的输出功率和电流在外界环境发生变化时，存在很强烈的波动，模型达到最大功率点所需时间长，跟踪速度慢。

稳态时，采用扰动观察法的光伏电池工作点在最大功率点附近出现振荡，且功率波动较大；采用模糊控制法的光伏电池工作点稳定在最大功率点，无振荡现象。

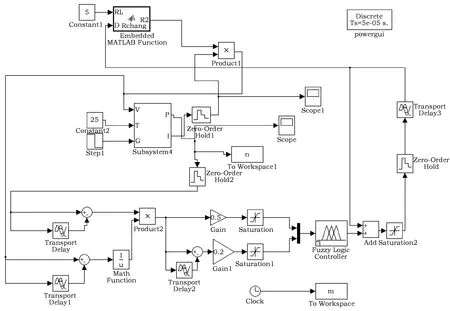
图8 光伏发电的模糊MPPT控制仿真图Fig.8 Simulation model of fuzzy control MPPT for PV power generation

图9 模糊控制功率跟踪图Fig.9 Power tracking diagram under fuzzy control

图10 模糊控制电流跟随图Fig.10 Current tracking diagram under fuzzy control

图11 扰动观察功率跟踪图Fig.11 Power tracking under disturbance observation

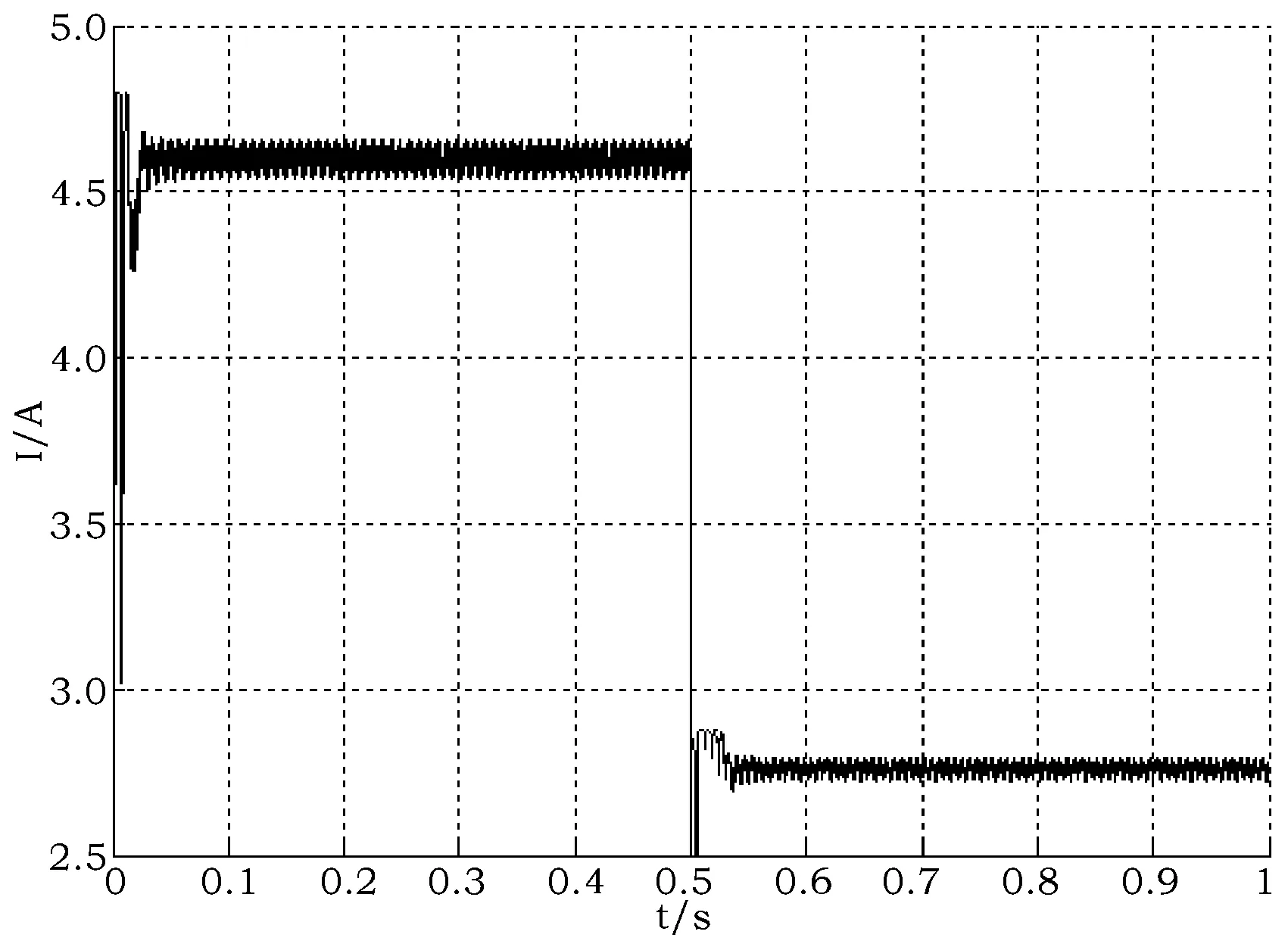
图12 扰动观察电流跟随图Fig.12 Current tracking under disturbance

4 结论

分析光伏电池等效模型的输出特性可知，光伏电池是一种非线性元件。本文在Matlab/Simulink环境下建立了光伏电池最大功率点跟踪控制的仿真模型，基于模糊控制的MPPT仿真结果与扰动观察法比较，模糊控制法表现出良好的控制性能，当外界光照强度发生变化时，实现了光伏系统最大功率点的快速跟踪，有效改善了系统在最大功率点附近的振荡现象，提高了系统的动态和稳态性能。

[1]徐锋.一种基于模糊控制的光伏发电系统的MPPT控制[J].电源技术,2014,38(1):92-96．

[2]王宝忠,王志兵.基于模糊控制的光伏系统最大功率点跟踪[J].哈尔滨理工大学学报,2012,17(4):13-17．

[3]赵争鸣,刘建政,孙晓英,等.太阳能光伏发电及其应用[M].北京:科学出版社,2005：1-4．

[4]王宝忠,刘卫法,付宁宁,等.光伏并网发电系统MPPT算法研究[J].科学技术与工程,2010,10(34):8432-8438．

[5]禹华军,潘俊民.光伏电池输出特性与最大功率跟踪的仿真分析[J].计算机仿真,2005,22(6):248-252.

[6]黄克亚.模糊PID控制在光伏发电MPPT中的应用[J].计算机仿真,2013,30(3):134-137.

[7]焦阳,宋强,刘文华.基于改进MPPT算法的光伏并网系统控制策略[J].电力自动化设备,2010,30(12):92-96.

[8]熊远生,俞立,徐建明.固定电压法结合扰动观察法在光伏发电最大功率点跟踪控制中应用[J].电力自动化设备,2009,29(6):85-88．

[9]Fermia N,Granozio D,Petrone G,et al.Predictive and Adaptive MPPT Perturb and Observe Method[J]. IEEE Transactions on Aerospace and Electronic Systems,2007,43(3):934-950.

[10]刘邦银,段善旭,刘飞,等.基于改进扰动观察法的光伏阵列最大功率点跟踪[J].电工技术学报,2009,24(6):91-94．

[11]卢松玉,徐国峰.时滞系统鲁棒IMC—PID控制器的研究[J].科技信息,2011(11):521-522．

[12]郭海霞,石明垒,李娟.基于matlab光伏发电系统的MPPT控制与仿真[J].山西农业大学学报(自然科学版),2013,33(1):76-81，92．

[13]刘洋,王征,刘有昌.基于模糊控制法的最大功率点跟踪研究[J].科技视界,2013(34):8-9，14．

[14]诸静.模糊控制原理与应用[M].北京:机械工业出版社,2005:358-390．

[15]D Shmilovitz.On the Control of Photovoltaic Maximum Power Point Tracker via Output Parameters[J]IEE Proceedings-Electric Power Applications,2005,152(2):239-248.

[16]郭红全.基于模糊控制MPPT的单相光伏发电系统的仿真研究[J].青海大学学报(自然科学版),2012,30(1):14-19．

[17]邹学毅,朱学忠.变结构参数模糊控制在光伏发电最大功率点跟踪中的应用[J].低压电器,2011(22):23-26，31．

[18]向导.模糊液位控制器在西门子PLC中的实现[D].上海:华东理工大学,2012.

MPPTfuzzylogiccontrolandsimulationforPhotovoltaicPowerGeneration

GuoHaixia

(CollegeofEngineering，ShanxiAgriculturalUniversity，Taigu030801，China)

[Objective]In order to improve the efficiency of Photovoltaic Power Generation，it is necessary to make the photovoltaic battery work quickly at the maximum power point through the Maximum Power Point Tracking control.[Methods]The equivalent model of photovoltaic battery was introduced，its output characteristic was analyzed， and fuzzy logic controlmethod was applied to maximum power point tracking control of photovoltaic battery. The simulation model of fuzzy controlmethod was established based on the Matlab/Simulink.[Result]The simulation result showed that the fuzzy control，improved the oscillation of maximum power point and had good steady-state and dynamic performance method could track the photovoltaic battery maximum power point rapidly.[Conclusion]The fuzzy controlmethod improved the oscillation of maximum power point， system had good steady-state and dynamic performance.

Maximum power point tracking, Fuzzy control, Photovoltaic battery, Simulation

2017-05-15

2017-07-03

郭海霞(1977-)，女(汉)，山西平遥人，讲师，博士，研究方向：检测技术、电力系统运行与控制

S214.9; TM615

A

1671-8151(2017)11-0825-06

(编辑：李晓斌)