油松根系力学性质有限元算法

沙斌，梁文俊

(1.嘉兴学院南湖学院， 浙江 嘉兴 314001； 2.山西农业大学 林学院, 山西 太谷 030801)

油松根系力学性质有限元算法

沙斌1，梁文俊2*

(1.嘉兴学院南湖学院， 浙江 嘉兴 314001； 2.山西农业大学 林学院, 山西 太谷 030801)

[目的]研究油松根系力学性质。[方法]本文用线性强化塑性模型对油松单根的本构关系进行模拟，通过塑性力学折线理论的有限元算法自编计算程序，分别对油松根系的双曲线模型和线性强化模型的应变进行计算，并与实测应力应变曲线的相应值进行对比分析。[结果]证明了线性强化模型不仅简单易行，且计算值与实测值的误差小，比双曲线模型的误差率小1到2个数量级。[结论]塑性力学折线理论的有限元算法简单易操作，可自编有限元计算程序，无论是双曲线模型还是线性强化塑性模型，都可以用塑性力学折线理论进行求解，比经典的增量塑性力学有限元算法有很大优势。

本构关系； 有限元方法； 油松根系； 拉伸应力

林木根系对于土壤有锚固加筋的作用，可增强土体的稳定性，对于边坡防治、水土保持等领域有着重要作用[1]，国内外已有相关研究人员对林木根系的力学性质进行研究。林木根系的力学特性具有各向异性和非均匀性等特点，一般通过根系拉伸实验得到根系的抗拉特性曲线。林木根系的抗拉特性与很多因素有关。宏观上和树种、根系直径、根系长度、根系含水率、当地环境、季节、土壤等有关。微观上和根系的化学成分有关。林木根系的拉伸曲线还与试验过程有关，比如拉伸速率、标距等因素。

林木根系抗拉特性的影响因素过多，导致研究时需要考虑的变量繁杂，给研究工作带来困难。国内外学术界还缺乏对根系力学性质统一的表达形式,目前对于根系的抗拉特性的研究，主要的研究方向是对不同的林木根系进行抗拉研究。其中，油松根系在受拉时，其抗拉特性曲线主要表现为前期弹性阶段，后期塑性阶段。油松根系受拉时的破坏类型是正向塑性断裂，断裂面不光滑，并伴随有明显的颈缩现象。油松的本构关系和拉伸破坏类型可看做是弹塑性材料的表现形式。

1 油松根系分段本构关系

油松根系的本构关系分为弹性阶段和塑性阶段，以前的相关研究对其全阶段的本构关系用数值分析方法建模。其本构关系可用双曲线模型进行模拟。陈丽华等[2]进一步用抛物线模型进行模拟，和实测曲线有非常高的吻合度。但是材料的全阶段本构关系却将弹性阶段的特性覆盖掉，使得弹性阶段的求解复杂化，不利于问题求解[3]。而且对于有限元算法应用来说，全阶段非线性要求使用增量理论进行有限元求解[4]，使得算法复杂，运行缓慢。因此可通过分段函数进行求解，在油松根系的弹性阶段，使用线性方程进行模拟，而在塑性阶段仍旧使用具有高吻合度的双曲线模型或者抛物线模型进行模拟。考虑到材料在弹塑性分界点的连续性，需对塑性阶段的曲线模型参数进行修正。本文拟使用线性强化塑性模型与双曲线模型进行比较，选择吻合度较高的方法。

1.1 弹性阶段

在弹性阶段，油松根系的极限弹性应力σe可达到极限应力σb的50%～70%，此阶段弹性模量为Ee。其本构关系可表达为式(1)：

σ=Eeε

(1)

其中，σ是应力；ε是应变；Ee是弹性模量；σe是极限弹性应力；σb是极限应力。

1.2 塑性阶段

在塑性阶段，油松根系的本构关系可用双曲线模型或抛物线模型进行拟合。下面对双曲线模型和二阶抛物线模型和分别介绍[5]。

1.2.1 双曲线模型

双曲线模型本构关系表达式为式(2)

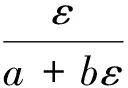
(2)

其中，a、b是模型试验参数：a是应力应变曲线的初始切线斜率倒数；b是破坏应力渐进值的倒数。双曲线模型对全阶段本构关系的模拟有一定的偏差，尤其是弹性阶段的偏差较大。现在改用分段模拟的方法直接避免了弹性阶段带来的偏差，使计算精度有一定提高。

1.2.2 二阶抛物线模型

(3)

其中，σb是极限应力；εb是极限应变；A、B是模型试验参数。

二阶抛物线模型和实测值的吻合度较好，相对于双曲线模型有所改善。但是依然不能很好的表达弹性阶段的本构关系。

2 油松根系基于折线理论的有限元算法

2.1 塑性力学折线理论

20世纪80年代以后，李铀提出塑性力学的一种新的研究方向—塑性力学折线理论[6]，折线理论的优势是在不引入屈服准则的情况下，准确的计算出结构的应力、应变和位移。塑性力学折线理论在塑性本构关系上来说，既不是全量理论，也不是增量理论，而是另辟蹊径，避免了直接建立应力和应变之间的关系，或者是应力和应变增量之间的关系，选择了建立了应力和弹性应变之间的关系，以及塑性应变和弹性应变之间的关系。如此就可以将非线性问题通过折线转化成线性问题，即塑性力学中的应力和弹性应变之间的关系应按照弹性力学应力应变的规律变化。弹性应变和塑性应变之间的关系我们简称为e—p关系或者e—p曲线，e—p曲线可以通过实验得出，也可以通过传统的应力应变曲线计算得到。塑性力学折线理论可以使用e—p曲线这种本构方程形式，也可以使用应力应变本构关系[7]。

塑性力学折线理论建立了统一基本方程组，将弹性阶段和塑性阶段的基本方程合二为一。统一基本方程组的张量方程表述如下[8]：

(4)

式一为弹性力学平衡方程的张量形式；式二是弹性阶段几何方程的张量形式；式三是弹性本构方程的张量形式；式四是e—p关系；式五是塑性阶段几何方程的张量形式。

当结构的应力状态处于弹性阶段时，方程(4)退化到前三式，即弹性力学基本方程组。

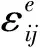
折线理论有限元算法提出了塑性阶段弹性应变矩阵的概念，采用直接迭代法求解结构的节点应变，避免了经典塑性力学有限元算法必须使用塑性矩阵进行增量求解的缺点，使得折线理论有限元的公式大大简化，更加准确的求解塑性力学问题。

2.2 弹性阶段有限元算法

2.2.1 弹性有限元基本矩阵

假设单元内任一点的位移是u、v、w可以由单元节点位移用函数表示，称之为位移模式。其表达式为[9]：

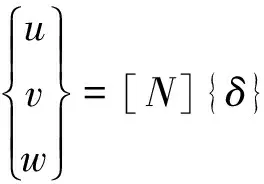
(5)

其中[N]称为形状函数矩阵，仅取决于单元的形状，在根系力学的分析中，可采用一维模型。由几何方程得[9]：

(6)

令：

(7)

[B]称为应变矩阵。

可以把几何关系改写成：

{ε}=[B]{δ}

(8)

由本构方程得：

(9)

令：

[D]=

(10)

称常数矩阵[D]为弹性矩阵，本构方程可用弹性矩阵表述如下：

{σ}=[D]{ε}=[D][B]{δ}

(11)

由虚功原理可推导出外荷载{p}和节点位移{δ}之间的关系。

{p}=[k]{δ}

(12)

其中单元刚度矩阵

(13)

2.2.2 弹性有限元解答过程

已知结构外荷载{p}，由式(12)解出节点位移{δ}。将节点位移{δ}分别带入式(11)和式(8)求出应力{σ}和应变{ε}。

2.3 塑性阶段有限元算法

2.3.1 塑性阶段的弹性应变矩阵

根据塑性力学折线理论的基本方程，塑性阶段的应力、应变的有限元形式如下：

{ε}=[B]{δ}

(14)

{σ}=[D]{ε}e

(15)

式中：{ε}是单元总应变；{ε}e是单元弹性应变。

若想求得应力{σ}，必须得到单元弹性应变和单元节点位移的关系，已知塑性阶段本构关系为：

σij=f(εij,α)

那么弹性应变为：

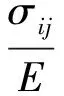
把式(14)带入上式得：

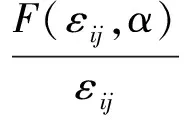
(16)

令

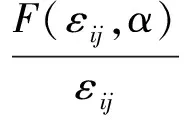
(17)

[B]′是塑性阶段弹性应变矩阵[10]

得到：

(18)

由塑性阶段的弹性应变与应力之间的关系可知：

{σ}=[D][B]′{δ}

(19)

根据虚功原理，得到塑性阶段的单元刚度矩阵表达式是：

(20)

求出塑性阶段的弹性应变矩阵[B]′的意义在于，可以根据式(20)得到结构的弹塑性刚度矩阵[K]，进而根据式(12)得到单元节点位移{δ}，根据式(19)得到结构的应力函数{σ}，根据式(14)得结构的应变函数εij。

2.3.2 塑性有限元解答过程

如式(17)所示，[B]′的表达式里的含有还未求出的应变函数εij，这是一个迭代求解的过程，可使用直接迭代法，选取初始值反复迭代可求出最终的结果。

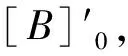
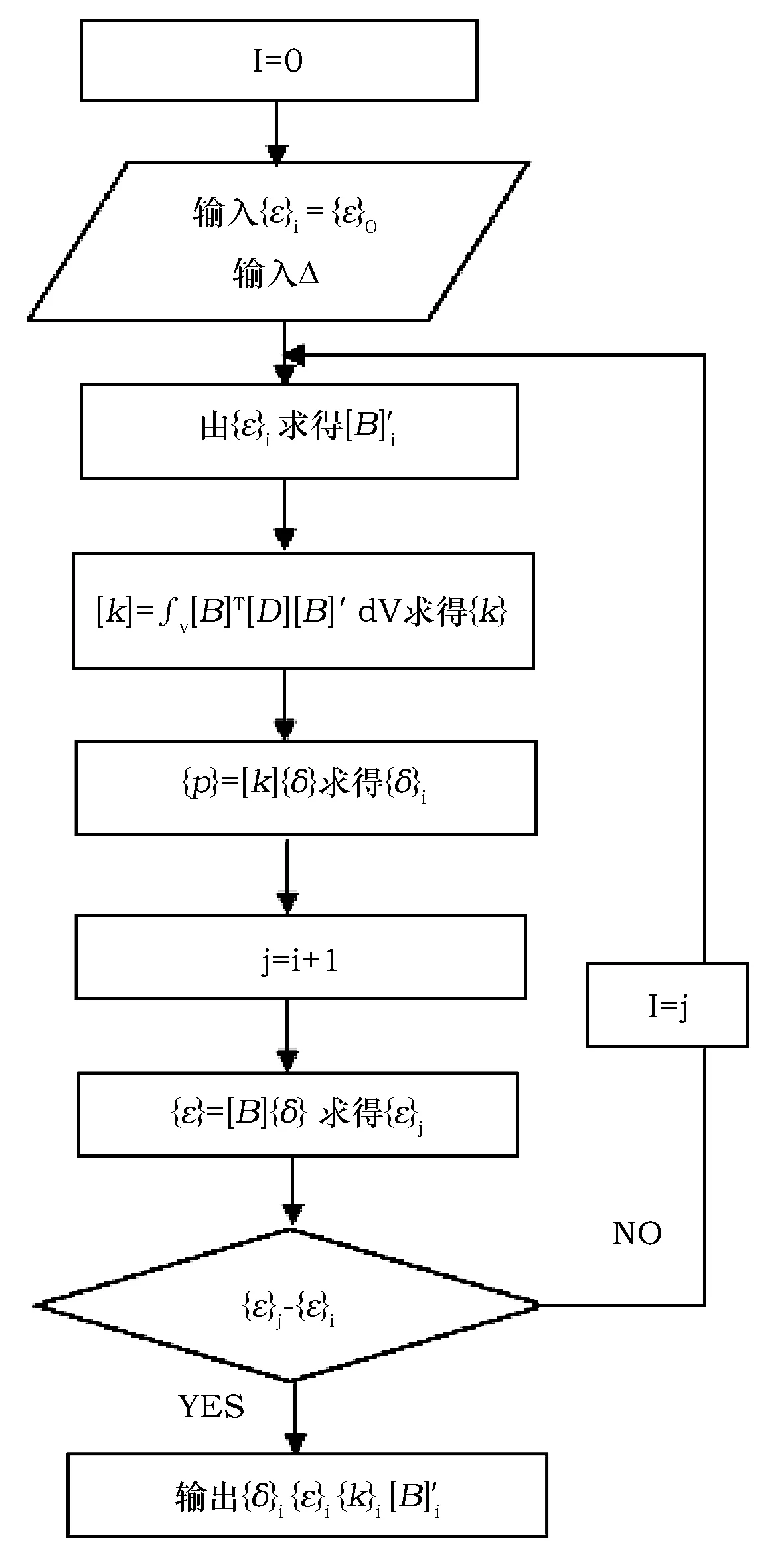
图1 计算[B]′流程Fig.1 Calculation flow chart

2.4 油松根系塑性阶段弹性应变矩阵

现以双曲线模型为例，说明油松根系塑性阶段弹性应变矩阵的求法。双曲线模型的本构关系为：

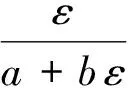
得到：

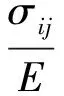
由式(16)得：

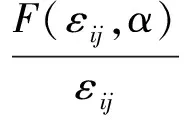
油松根系塑性阶段弹性应变矩阵的表达式为：

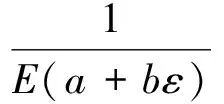
(21)

3 结果与分析

3.1 单根拉伸试验

拉伸试验所用到的仪器是电子测量仪(KX3900)。用电子拉力传感器记录拉力(P)，用百分表记录根系位移(S)，采用控制应变法进行加载，每次应变量为0.005%，以秒表来控制两级加载之间的时间间隔，即加载速率。采集生长正常的新鲜油松主根，分为3组，1号组为幼龄油松根系，2号组为中龄油松根系，3号组为成熟油松根系。它们的标定长度为40 cm，根径分别为7.57 mm、10.5 mm和7.79 mm。试验结果可绘成工程应力(σ)—工程应变(ε)曲线(详见图2)。

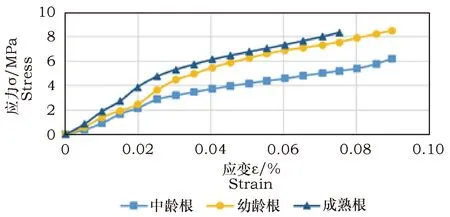
图2 实测应力应变曲线图Fig.2 Measured stress strain curve chart

记录各根断裂时的应力应变，即各根的抗拉强度σb和极限应变εb，根据σ-ε曲线，计算出对应于40%的σb时割线模量E0.4[11]，以及单根在极限状态下的割线模量E1.0。结果如表1所示。

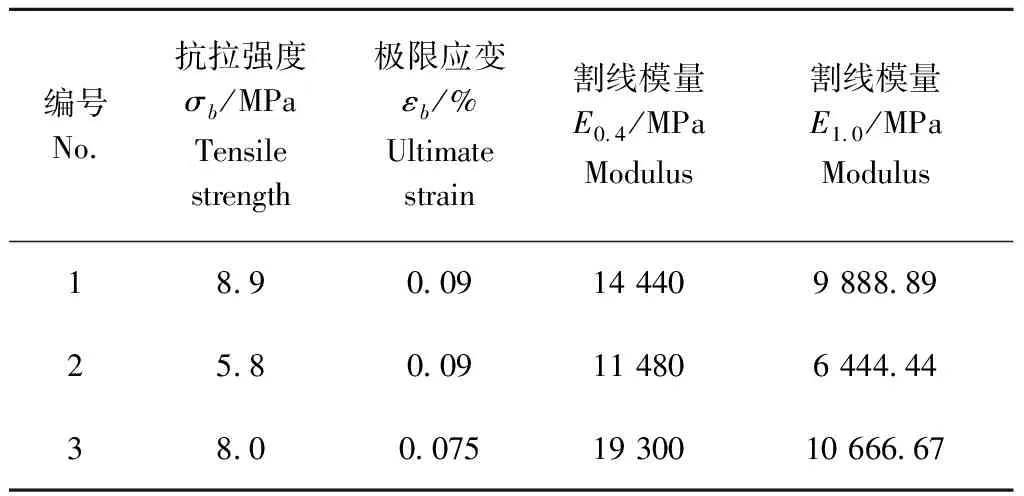
表1 数据分析Table 1 Data analysis

3.2 有限元代码计算

3.2.1 塑性双曲线

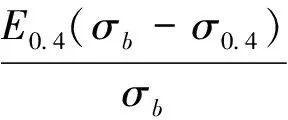
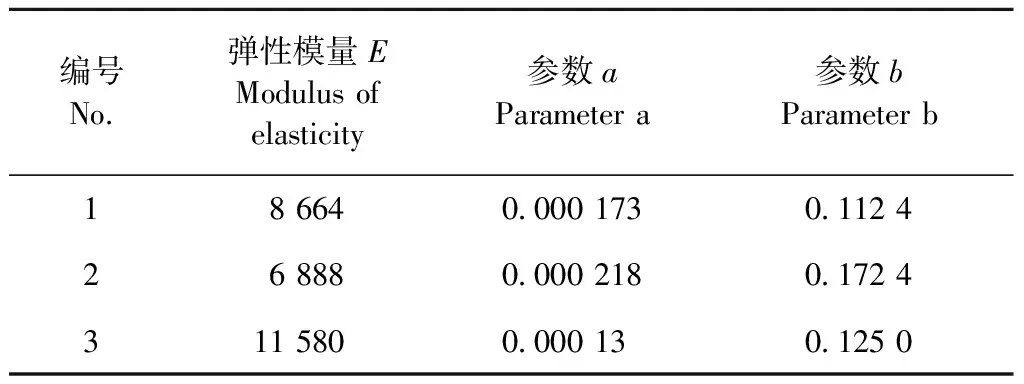
表2 双曲线参数Table 2 The hyperbolic parameters

选用八节点单元模拟单根受拉应力状态，根据实测应力应变曲线图，令拉伸应力p=3MPa，此时幼龄根(1号)处于弹性阶段、成熟根(3号)处于弹塑性过度阶段、而中龄根(2号)处于塑性阶段。故而此拉伸应力p具有充分的代表性。

由于单根拉伸时侧向的应力应变不是主要的变形和破坏方向，主要关心的是沿着拉伸方向的应力应变，所以其塑性流动判据可使用最大拉应力理论，认为纵向应力σ超过σ0.4时，油松的根进入塑性阶段。

MATLAB程序进行计算[12,13]，求得幼龄根对应的应变为0.035%，中龄根对应的应变为0.054%，成熟根对应的应变为0.025%。与实测σ-ε曲线中的应变误差率如表3所示。

表3 双曲线模型应变误差率Table 3 Strain error rate of hyperbolic model

可看出用双曲线模型带来的误差相当大。

3.2.2 线性强化塑性模型

观察实测σ-ε曲线，是良好的线性强化模型，弹性应力σe≈σ0.5，这里取1号弹塑性分界应变为0.03%；2号弹塑性分界应变为0.025%；3号弹塑性分界应变为0.025%。线性强化模型的参数见表4。

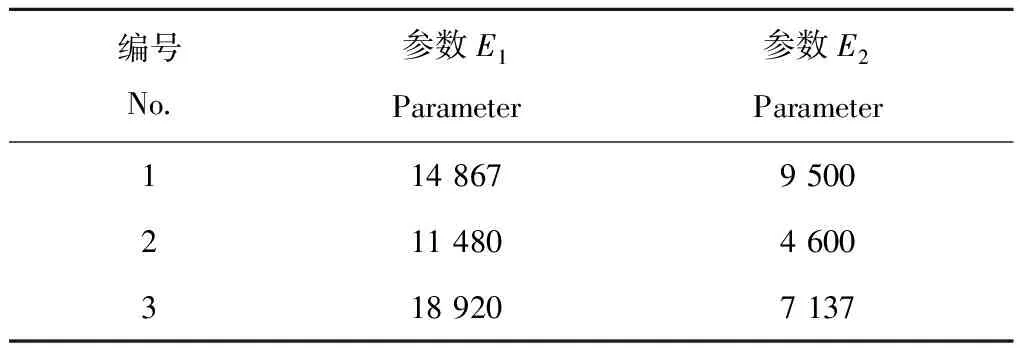
表4 线性强化模型参数Table 4 Parameters of linear hardening model

依然令拉伸应力p=3 MPa，用MATLAB程序进行计算，与实测σ-ε曲线中的应变误差如表5所示。可看出用线性强化塑性模型进行数值模拟，得到的结果较好，其误差比双曲线模型小1～2个数量级。

表5 线性强化模型应变误差率Table 5 Strain error rate of linear hardening model

4 结论

(1)线性强化模型的构建比较简单，而且从上述结果的误差可看出，在外荷载一定时，用线性强化塑性模型可更好的模拟真实应变值，线性强化模型的误差比双曲线模型的误差小1～2个数量级，计算模拟结果与实测差值结果的误差仅在10%以内，取得了很好的结果。从计算结果上看，线性强化模型更吻合实测应力应变曲线。

(2)油松根系的塑性阶段弹性应变矩阵[B]′表达形式简单，迭代过程清晰。塑性力学折线理论的有限元算法比全阶段增量的经典塑性力学有限元算法更简单，用自编软件进行计算简单易行。

(3)无论是何种模型，只要分段成弹性阶段和塑性阶段，并保证弹塑性分界点连续，均可用塑性力学折线理论的有限元算法解决根系力学分析问题，对于已经测定一维本构关系的根系种类，比如油松根系，用塑性力学折线理论的有限元算法可以很好的进行求解。

[1]雷相科，张雪彪，杨启红，等.植物根系抗拉力学性能研究进展[J].浙江农林大学学报,2016,33(4):703-711.

[2]盖小刚.林木根系固土力学特性研究[D].北京：北京林业大学，2013.

[3]欧文，辛顿，曾国平.塑性力学有限元——理论与应用[M].北京：兵器工业出版社，1989：10-100.

[4]李铀，彭意.塑性力学问题的一种近似算法[J].岩石力学与工程学报，2003,22(3)：378-382.

[5]曹云生,陈丽华,盖小刚,等.油松根系的固土力学机制[J].水土保持通报,2014，34(5):6-10，14.

[6]李铀.材料强度理论新探[J].工程力学，1988,5(1)：15-17.

[7]Li Y.New Research on the Stress Field of Elastic-Plastic Small Deformation Problems[J].Journal of Materials Processing Technology,2003,138(1):508-512.

[8]李铀.塑性力学引论[M].北京：科学出版社,2008:1-178.

[9]赵经文，王宏钰.结构有限元分析(第二版)[M].北京：科学出版社,2001:1-100.

[10]王勖成.有限单元法[M].北京：清华大学出版社，2003：1-300.

[11]陈欣，李铀.基于e-p曲线的塑性力学新方法的有限元算法[J].湖南城市学院学报(自然科学版)，2012,21(4)：1-4.

[12]刘秀萍.林木根系固土有限元数值模拟[D].北京：北京林业大学，2008.

[13]王沫然.MATLAB与科学计算(第2版)[M].北京：电子工业出版社，2004:1-150.

[14]P.I.Kattan.MATLAB有限元分析与应用[M].北京：清华大学出版社，2004：1-100.

ThefiniteelementmethodinPinusTabulaeformisroots

ShaBin1,LiangWenjun2*

(1.JiaxingUniversityNanhuCollege,Jiaxing314001，China； 2.CollegeofForestry,ShanxiAgriculturalUniversity,Taigu030801，China)

[Objective]In order to study the mechanical properties ofPinustabulaeformisroot,[Methods]simulating the constitutive relation ofpinustabulaeformisroot with the linear hardening plasticity model, and write a calculation program with finite elementmethod of broken line theory in plastic mechanics. To compute the strain of root, through the model of linear hardening and hyperbola, respectively, and compared it with the measured value from the stress-strain curve.[Results]It proved that the linear hardening model was not only simple, but also had a smaller error, which was about 1 to 2 orders of magnitude less than that of the hyperbolic model.[Conclusion]The finite elementmethod of broken line theory in plastic mechanics was simple and easy to write a calculation program, which could compute both the model of linear hardening and the model of hyperbola, in which case, it had great advantage over the classical one.

Constitutive relation, Finite element method,Pinustabulaeformisroot system, Tensile stress

2017-04-20

2017-07-03

沙斌(1989-)，男(汉)，江苏邳州人，助教，硕士，研究方向：计算力学

*通信作者：梁文俊，副教授，硕士生导师，Tel:0354-6288329；E-mail:liangwenjun123@163.com

国家自然基金(31500523)；山西农业大学引进人才科研启动资金(2014YJ19)

S791; Q947.1；O245；O344.1

A

1671-8151(2017)11-0798-07

(编辑：韩志强)