国际大型测评项目中等值技术的应用与启示

王烨晖 张缨斌 杨涛 辛涛

（北京师范大学，北京 100875）

国际大型测评项目中等值技术的应用与启示

王烨晖 张缨斌 杨涛 辛涛

（北京师范大学，北京 100875）

国际大型测评项目在年度内题本等值时，主要采用同时估计的方法实现对题目参数的估计，并使用似真值实现对学生个体能力的报告，各个测评项目之间的等值设计与处理相对统一与一致。在年度间等值时，不同的项目，依据各自的设计特点，采用锚题或锚人的方法，使用同时估计，并通过线性转换将学生能力分数置于同一量尺上，实现年度间分数的比较。依据我国国情，建议采用锚题与锚人相结合的等值设计方式实现年度间测评结果的链接。

等值；链接；题本设计；大规模测评

国际大型测评项目日益受重视，不仅因其有助于人们评估学生的学习现状和教育目标的达成情况，还因其有助于研究者全面考察学生发展的影响因素，为教育政策的制定提供客观依据。但这些测试都面临着同样的问题——广泛的测试内容与有限的测试时间之间的矛盾。为了解决该问题，矩阵抽样的多题本设计技术应运而生：根据测试内容开发一套完整的试题，然后把试题划分成若干小套试题，每一小套试题就是一个题本，每个学生只作答其中的一个题本[1]。为了让学生的测试分数具有可比性，就需要运用等值技术，把作答不同题本的学生的测试分数链接（linking）到同一量尺上，即年度内等值。

仅凭一次测试结果，并不能提供充足而稳定的信息。国际大型测评项目越来越重视开展追踪或趋势研究。从2003年国际教育成就评价协会（In⁃ternational Association for the Evaluation of Education⁃al Achievement）将其负责的一个项目的名称由Third International Mathematics and Science Study变更为Trends in International Mathematics and Science Study可以看出，趋势研究已成为TIMSS的一个关注点。和年度内等值类似，若需要分析学生测试表现的发展趋势，就得保证不同年度的测试分数具有可比性。此时，也需要用到等值技术，将不同年份学生的测试分数转换到同一量尺上，即年度间等值。

1 年度内等值

1.1 PISA

1.1.1 题本设计

在2012年及之前，PISA采用平衡的不完全组块设计（balanced incomplete block design，BIB）进行题本的设计。以2012年为例，所有题目组成13个题组：7个数学题组，3个阅读题组和3个科学题组。在将题目分配到各题组中时，一方面会尽量使每个题组所需的作答时间相同；另一方面，会使同一科目不同题组所含的题目在内容维度和认知维度上的分布尽量相近。不同题组间无相同题目。划分好题组后，4个题组构成一个题本，题组的两两组合在所有题本中均不重复，共有13个题本。每个题组在题本的4个组块位置均出现一次，以平衡可能存在的顺序效应。在这种设计中，大部分题本在不同科目上的题量存在差异，这种差异有可能给学生作答带来影响[2]。为了降低这种影响，PISA2015的题本设计中，大部分题本只考查某两个科目，且两个科目的题量相同。由于一个题本只能考查两个科目，PISA2015的纸笔作答题本数量多达30个。

1.1.2 等值方法

PISA在进行年度内等值时采用的是同时标定法，在一次参数估计过程中同时估计所有题本的题目参数和能力参数[3]。具体做法为：将两个或更多题本的数据合并，对其中由于题本设计造成的缺失，在估计软件中将相关题目标识为未施测。以PISA2012为例，首先从每个国家随机选取500个学生，组成一个标定样本；其次，根据标定样本的作答数据标定所有题目参数；最后，根据题目参数估计所有学生的能力参数（似真值①除了IRT模型、题目参数和学生作答数据，PISA、TIMSS和NAEP还会结合一些背景变量（或对背景变量进行主成分分析后提取得到的变量），对学生的能力参数分布进行估计。然后，从能力参数分布中抽出5个值代表学生能力。这5个值被称为学生能力的似真值（plausible value）。）。

PISA2015中，仍然采用同时标定法，但与以往的做法有3点不同：（1）以往PISA采用单参数模型（包括one parameter logistic model和partial credit model，即1PLM和PCM），PISA2015采用的是两参数模型（包括two parameter logistic model和generalized partial credit model，即 2PLM 和 GPCM）；（2）以往PISA在分析试题时，限定所有参与国家和地区共享相同的题目参数，即题目具有测量不变性。如果在事先的检验中发现某个题目在某个国家或地区上出现项目功能差异（differential item functioning，DIF），在标定题目参数时，该题会被设置成未施测给这个国家或地区的被试。相应地，在估计这个国家或地区的被试能力参数时，不使用这道题目。而PISA2015在标定题目参数时，在保证具有测量不变性的题目数量足够多的前提下，允许少量有DIF的题目在施测国家或地区偏离国际参数。一些研究认为这种做法在保证测验分数具有跨国家和地区可比性的同时，能提高测验公平性[4]；（3）PISA2015中的标定样本不仅包括2015年度的参与国家和地区的学生，还包括往年参加PISA测试的学生[5]。

1.2 NAEP

1.2.1 题本设计

NAEP主要包括国家测试、州测试、阅读和数学的长期趋势测试等几种类型，其题本设计主要为平衡的不完全组块设计（BIB）和部分平衡的不完全组块设计（partial balanced incomplete block design,pBIB）。不同学科、不同类型的测试会根据需要采用其中一种设计方式。BIB设计能够保证所有题组在各个组块出现次数相同，并且不同题组之间的组合频率相同。而pBIB设计则无法满足这样的要求。以NAEP2012数学长期测试采用的pBIB设计为例（见表1），每个题组在不同组块出现的次数不同，如题组M21在组块1和组块3上都出现了两次，但在组块2上只出现一次。在各个题本中都没有MX52和M24的组合。

1.2.2 等值方法

NAEP采用同时标定法估计所有题目的参数。对于选择题、二级计分的建构题和多级计分的建构题，分别使用3PLM、2PLM和GPCM等项目反应理论模型处理，并结合学生的背景信息，采用似真值报告学生个体的能力值。

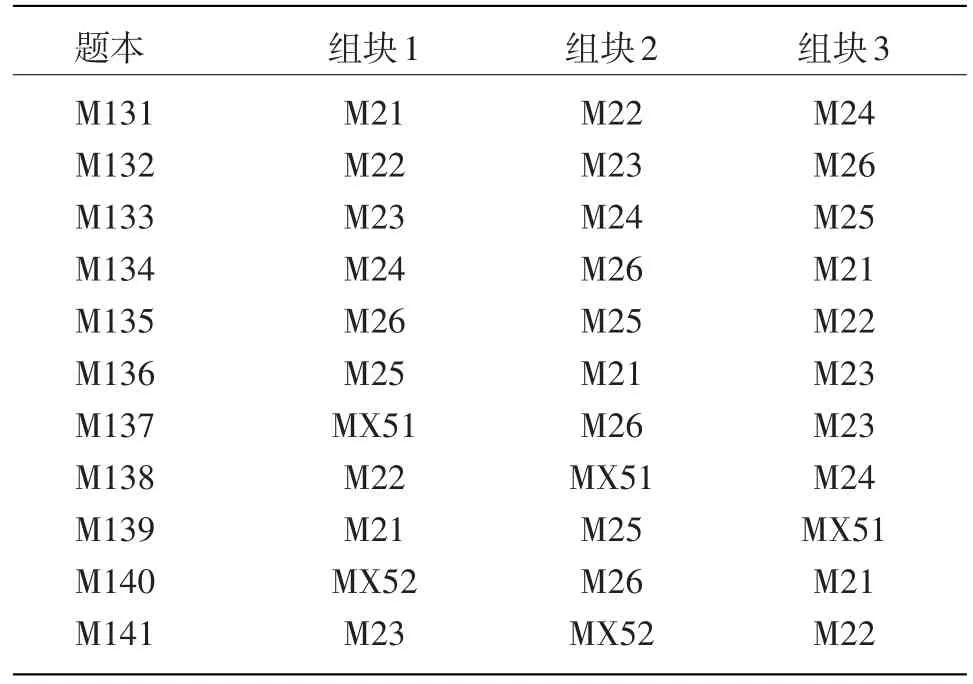
表1 NAEP2012数学长期趋势测试标准题本设计（9岁年龄段）[6]

1.3 TIMSS

1.3.1 题本设计

从2007年起，TIMSS一直采用同样的矩阵抽样设计对数学和科学两门学科进行测查：共14个题本，每个题本包括数学和科学两部分，每个学科有两个题组，即每个题本包括4个题组。每个题组的作答时间相近，同一科目不同题组所含的题目在内容维度和认知维度上的分布相近。不同题组以及不同学科按照螺旋的方式排列，以平衡题组和学科在不同题本上的顺序效应。

1.3.2 等值方法

TIMSS处理数据时采用的模型与NAEP非常类似，用同时标定的方法对所有题本进行同时估计，其中，选择题、二级计分的建构题和多级计分的建构题分别使用3PLM、2PLM和GPCM等进行处理[7]。TIMSS一直稳定使用这几个模型进行相应的参数估计，并结合学生的背景信息，采用似真值报告学生个体的能力值。

1.4 小结

PISA、NAEP和TIMSS三大项目在年度内等值设计方面比较相似，均采用矩阵抽样的方法进行题本分配，使用同时标定法实现对题目参数的估计，最后采用似真值进行学生能力的报告。PISA在2015年前，采用1PLM进行估计，此后采用2PLM和GPCM，与TIMSS和NAEP的估计模型更加一致。总体而言，在年度内等值方面，三个项目的做法比较一致。但三者对于学生来不及作答的题目处理有所不同。PISA2015中，如果某个学生没来得及作答位于题本末尾处的题目，未作答题目会被当作是没有给这位学生施测，而此前PISA的处理方式是把未作答题目当作学生答错的题目。NAEP分三种情况处理无时间作答题目：（1）无时间作答的选择题被设定为没有施测；（2）对于无时间作答的开放题，如果该题前一道也未作答，那么该题连同前一道题目都被设定为没有施测；（3）如果前一道题目被作答了，则设定为答错或完全答错。TIMSS在标定题目参数时，学生无时间作答题目会被设定为没有给这位学生施测，但在估计能力参数时，无时间作答题目则被设定为该学生答错的题目。

2 年度间等值

2.1 PISA

2.1.1 等值设计

PISA在进行年度间等值时采用非等组锚题设计，不同年度的测试之间通过趋势题（即锚题）进行链接。如果是该年度的主测科目，该科目的试题中有一部分是锚题，和上一个年度进行链接；若不是主测科目，则该科目的所有试题都是锚题。以PISA2012为例，主测科目数学共110道题，36道锚题；而阅读共44题，科学共53题，均为锚题。PISA2015为了提高年度间等值的准确性，增加了锚题的题量；科学为主测学科，总题量为184道，其中锚题85道；而数学共83题，阅读共103题，均为锚题。

2.1.2 2015年之前的等值方法

2015年之前，PISA进行跨年度等值时，采用了均值/均值法[8]。均值/均值法的原理认为，锚题在不同测试中的参数仅仅是量尺原点和单位不同，可以实现线性转换。通过计算锚题在不同年度的参数均值之差，得到等值常数，就可以把不同年度的测试分数转换到同一量尺上。以链接PISA2012和PISA2009的数学能力参数为例：首先，根据PISA2012标定样本对题目参数进行估计；然后，基于2012年题目参数估计值，估计2012年学生的数学能力参数值；最后，根据PISA2009标定样本得到的数学锚题难度均值，减去根据PISA2012标定样本得到的数学锚题难度均值，得到等值常数，为0.07 logit，PISA2012的能力参数加上0.07 logit后，就与PISA2009的能力参数在同一个量尺上了。要把PISA2012的数学能力参数转换到PISA数学量尺上，通过一定的线性转换即可实现，原理与上述步骤类似。

2.1.3 2015年的等值方法

PISA2015进行跨年度等值时，采用的是同时标定法。具体步骤如下：

（1）PISA2015标定题目参数所用的标定样本，不仅包括PISA2015的参与国家和地区的学生，还包括最近三轮测试（即PISA2012、PISA2009以及PISA2006）参与国家和地区的学生。因为2015年之前，PISA用的都是单参数模型，所以PISA2015在标定题目参数时，限定2012年、2009年和2006年三个年度的所有题目以及2015年度的锚题的区分度相同，以降低使用两参数模型进行参数估计可能带来的影响。此过程中，4个年度的题目都是放一起进行参数标定的，所以得到的题目参数都处于同一量尺上。

（2）根据（1）中得到的题目参数估计PISA2015的学生能力参数，同时重新估计PISA2012、PISA2009以及PISA2006的学生能力参数。因为所用的题目参数都在同一量尺上，所以这个过程得到的各轮测试的能力参数也在同一量尺上。

（3）过程（2）中得到的PISA2012、PISA2009以及PISA2006学生能力参数，与对应年度的学生PISA量尺分数（用于结果报告中的分数）存在线性转换关系。根据这种线性转换关系，并且根据某科目为主考科目的那一轮数据，计算该科目的转换系数。例如，PISA2006的主考科目为科学，那么根据过程（2）中得到的PISA2006学生科学能力参数与PISA2006学生科学量尺分数间的转换关系，就可以计算科学科目的转换系数。计算公式如下：

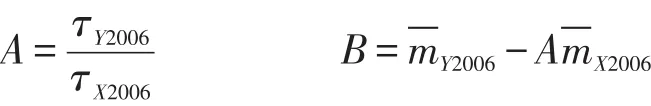
（4）过程（2）得到的各轮测试能力参数都在同一量尺上，那么就可以根据过程（3）得到的各科目转换系数，将过程（2）中得到的PISA2015学生能力参数转换到PISA量尺上，用于后续的数据分析和报告撰写。以科学为例，转换公式如下：

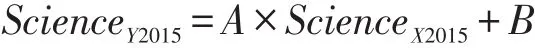
ScienceX2015代表过程（2）得到的PISA2015学生科学能力参数，ScienceY2015代表PISA2015学生科学量尺分数。

今后，PISA测试将沿用这一做法进行跨年的等值，例如PISA2018在标定题目参数时，标定样本将涉及PISA2018、PISA2015、PISA2012和PISA2009的学生。然后按照上述步骤，将PISA2018的学生能力参数转换成PISA量尺分数。

2.2 NAEP

2.2.1 等值设计

（1）NAEP的国家测试

NAEP的国家测试采用锚题的方式实现年度间的等值。以数学为例，2011年的数学测试（四、八年级）有10个题组，其中8个题组来源于2009年测试，四、八年级的8个2009年题组又分别有5个题组和4个题组来自于2007年的测试。

（2）NAEP的长期趋势测试

NAEP的阅读和数学长期趋势测试每4年一轮，针对9岁、13岁和17岁的学生进行[9]。阅读和数学的长期发展趋势分别可以回溯到1971年和1973年。为了实现长时间对学生学业发展的追踪研究，长期趋势测试的工具一直保持稳定不变。2004年，NAEP对其长期趋势测试进行了唯一一次较大的调整，主要包括：删除科学和写作测试；面向残疾和非英语母语的学生开放；更新不合时宜的题目；更新背景问卷并与测试卷分离；语文和数学单独成册；调整实施流程。

2.2.2 等值方法

（1）NAEP的国家测试

由于存在大比例的锚题，NAEP的国家测试中各学科相邻轮次之间的测试通过同时估计和线性转换便可将结果置于同一量尺上。

（2）NAEP的长期趋势测试

由于2004年的长期趋势进行了较大的改动，因此2004年之后的测试结果与2004年之前的测试结果无法简单地通过同时标定来实现统一量尺化。为了降低这种改动可能对等值结果造成的影响，NAEP采用了随机等组设计（randomly equivalent samples design）来解决这个问题[10]。2004年度的长期趋势测试编制了两套测试工具，一套是与旧有测试相同的工具，称之为桥测验（bridge assessment），另一套则是根据新设计编制的修订版工具（modi⁃fied assessment），把2004年的学生样本随机分为两个同质样本，将修订后的2004年长期趋势测试施测给一个样本，将旧版2004年桥测验施测给另一样本[11]。因为两个样本是同质的，所以有着相同的能力分布，据此可以计算转换系数，实现新版2004年长期趋势测试分数与旧版2004年长期趋势测试分数的链接。通过同时估计，新版2004年长期趋势测试的结果能和之后的所有长期趋势结果进行链接，而旧版2004年长期趋势测试的结果则能够和2004年之前所有的长期趋势测试结果进行链接，加之2004年随机等组设计的这个桥梁，NAEP能够实现所有年份长期趋势结果的链接。

2.3 TIMSS

2.3.1 等值设计

以TIMSS2015为例，包括14个数学题组和14个科学题组，其中8个数学题组和8个科学题组来自于TIMSS2011，以保证能在TIMSS2015和TIMSS2011之间进行等值。

2.3.2 等值方法

TIMSS年度间的等值方法与NAEP类似，一贯的做法是，年度内等值和跨年度等值同时进行，把相邻测试轮次的学生作答数据放一起，对题目参数进行同时标定。首先，TIMSS把2015年所有学生的作答数据和2011年所有学生的作答数据放一起，同时标定题目参数；其次，估计学生能力参数。因为使用在同一量尺上的题目参数估计2011年度和2015年度的学生能力参数，所以得到的两个年度的学生能力参数在同一量尺上。后续处理与PISA2015类似。以数学为例，计算公式如下：

MathX2015代表TIMSS2015学生科学能力参数，MathY2015代表TIMSS2015学生科学量尺分数。

2.4 小结

在跨年度等值中，三大项目的做法既有共同之处，又各有特色。三者之间均采用锚题设计的方式，通过同时估计实现各轮次之间的跨年度等值，但不同项目同时进行估计的轮次数量不同。PISA测试阅读、数学和科学，每一轮次只有一个主测学科。因此，为了实现同一学科跨轮次之间的比较，需要至少对4轮次测试进行同时估计，才能实现主测学科的跨年度比较。NAEP的主测验分学科进行，每次只需和其相邻的测试轮次进行同时估计即可。TIMSS每个轮次都全面测查数学和科学，因此相邻轮次的共同估计便可实现年度间等值。

NAEP的长期趋势测验需要对青少年的学业发展进行长期的趋势描述，因此整体设计与其主测验及PISA和TIMSS均不相同。它要在较长的时间内保持工具的稳定性，因此通过同时估计可以直接进行多年的结果比较。但是，课程体系随着时间在不断进行调整变化，测评技术也在不断改进与提升。因此，这样的长期趋势测验也需要有相应的改动与更新。在长期趋势测验改动更新的年份，则通过随机等组的方式（即锚人的方式）实现新旧版本测试之间的链接。

3 启示

在大规模的学业测评中，矩阵抽样设计已经成为题本设计的主要方式，切实解决了广泛测试内容和有限测试时间之间的矛盾。随着矩阵抽样设计的兴起，势必面临着题本之间的等值和报告学生个体学业成绩。就当前来看，题本间的等值（即年度内等值）利用锚题对参数进行同时估计，并且合理处理好学生未能完成题目的缺失，能够较精确实现项目参数的估计。年度间的结果比较（即跨年度等值设计）面临着更多的问题，如何选择合适的等值方案与测验本身的设计、测验目的密不可分。

考试在我国向来是一项高风险、高利害关系的事业。无论是中考、高考，抑或是国家教育质量监测，横向单次的测试结果所能提供的信息有限。我们希望能够通过纵向的比较，提供学生学业的动态发展状况或者教育发展趋势。如果是要进行较为严格的追踪趋势研究，测评工具需要相对稳定（例如NAEP的长期趋势研究），但测试完成之后会曝光所有题目，这对中考、高考等高风险测试并不适合。如何将不同年度或者测试轮次之间的结果进行链接，是准确报告发展趋势的关键所在。

年度之间的链接主要通过锚题和锚人两种方法实现。若采用锚题设计，为保证估计的稳定性，减少估计的误差，各大项目中锚题占总题量的比例至少在50%左右，且锚题不仅仅只是在相邻的测试轮次之间，在多个轮次的测试之间都可能存在共同的题目。但是一半以上的锚题，甚至多轮次使用，可能会造成锚题过度曝光，引发练习效应，影响链接的准确性。

采用锚人设计，若采用同一批考生完成两套试卷，那么这批考生需要对总体具有很好的代表性，对抽样设计要求较高。此外，考生需要完成两套测试卷，对考试的组织实施提出了更高的要求。若采用随机等组设计，则需要实现对考生进行相应的分组，保证两组学生之间完全“等价”，在两个组中匹配考生成为保证等值效果的关键所在。

就我国国情而言，完全采用锚题设计，可能会导致锚题过度曝光，但若完全采用锚人设计，如果是随机等组设计，一方面对等组的要求比较高，不容易实现；另一方面，两组考生作答两份不同的试卷，社会大众不易理解。如果单组设计，同一批被试同时完成两份试卷，一方面具体实施的可行性不大；另一方面样本的代表性不易得到保证。如果能够将锚题设计与锚人设计结合起来使用，适当减少锚题占总题量的比例，降低锚题曝光程度，同时在部分代表性的区域采用随机等组设计或单组设计，实现年度间的稳定等值链接，可能是适合我国国情的一种有效设计。

[1]李凌艳,辛涛,董奇.矩阵取样技术在大尺度教育测评中的运用[J].北京师范大学学报（社会科学版）,2007（6）:19-25.

[2]OECD.PISA 2012 Technical Report[M].Paris:OECD Publishing,2014.

[3]WINGERSKY M S,LORD F M.An investigation of methods for re⁃ducing sampling error in certain IRT procedures[J].Applied Psycho⁃logical Measurement,1983（3）:52.

[4]OLIVERI M E,VON D M.Toward increasing fairness in score scale calibrations employed in international large-scale assessments[J].International Journal of Testing,2014,14（1）:1-21.

[5]OECD.PISA 2015 Results Volume I:Excellence and Equity in Edu⁃cation[M].Paris:OECD Publishing,2016.

[6]NCES.Student booklets for the 2012 mathematics long-term trend assessment[EB/OL].（2014-06-02）[2017-04-18].https://nces.ed.gov/nationsreportcard/tdw/instruments/2012/cog_dev_math_booklets 2012.aspx.

[7]MARTIN M O,MULLIS I V S,HOOPER M.Methods and proce⁃dures in TIMSS 2015[Z].Chestnut Hill,MA:TIMSS&PIRLS Inter⁃national Study Center,Boston College,2016.

[8]MARCO G L.Item characteistic curve solutions to three intractable testing problems[J].Journal of Educational Measurement,1977,14（2）:139-160.

[9]NCES.How were the NAEP long-term trend assessments devel⁃oped?[EB/OL].（2013-06-25）[2017-04-18].https://nces.ed.gov/nationsreportcard/ltt/howdevelop.aspx.

[10]NCES.Development of the long-term trend cognitive items and in⁃struments[EB/OL].（2014-06-02）[2017-04-18].https://nces.ed.gov/nationsreportcard/tdw/instruments/cog_dev_ltt.aspx.

[11]NCES.2004 Bridge study[EB/OL].（2013-06-25）[2017-04-18].https://nces.ed.gov/nationsreportcard/ltt/bridge_study.aspx.

Applications and Implications of Test Equating in Large-scale International Educational Assessments

WANG Yehui,ZHANG Yingbin,YANG Tao,XIN Tao
（Beijing Normal University,Beijing,100875,China）

To link scores of different test booklets from the same cycle to the same scale,large-scale international educational assessment programs mainly use concurrent calibration to estimate item parameters.Plausible values are used as students’ability scores.The equating designs and methods are relatively consistent across different assessment programs.To link scores of different tests from different cycles to the same scale,common item design or equivalent groups design,the concurrent calibration and the method of linear transformation are used in educational assessment programs.As for China’s situation,this paper suggests the national assessment use the equating designs of the combination of the common item design and the equivalent groups design to link test scores from different cycles to the same scale.

Equating;Linking;Booklet Design;Large-scale Assessment

G405

A

1005-8427（2017）08-0043-7

10.19360/j.cnki.11-3303/g4.2017.08.008

王烨晖（1982—），女，北京师范大学中国基础教育质量监测协同创新中心，讲师；

张缨斌（1993—），男，北京师范大学教育学部，在读硕士；

杨 涛（1967—），女，北京师范大学中国基础教育质量监测协同创新中心，副教授；

辛 涛（1968—），男，北京师范大学中国基础教育质量监测协同创新中心常务副主任，教授。

（责任编辑：陈宁）