基于支持向量机的钛合金铣削加工参数优化

向国齐

(攀枝花学院 资源与环境工程学院，四川 攀枝花 617000)

1001-2265(2017)10-0134-04

10.13462/j.cnki.mmtamt.2017.10.032

2016-03-05；

2016-04-18

攀枝花市科学技术和知识产权局(0290100061)；四川省教育厅项目(13za0310)

向国齐(1974—)，男，四川泸州人，攀枝花学院副教授，硕士生导师，博士，研究方向为多学科设计优化及智能机电系统方面的研究，(E-mail)191870261@qq.com。

基于支持向量机的钛合金铣削加工参数优化

向国齐

(攀枝花学院 资源与环境工程学院，四川 攀枝花 617000)

针对钛合金材料在加工过程中受铣削力影响易于产生变形而影响加工效果，属难加工材料，为了保证加工质量，提高生产效率及降低加工成本，其切削加工参数的合理选择非常关键；对钛合金铣削加工进行有限元数值计算，结合试验设计方法构建了基于支持向量机的切削力预测模型，提出了一种基于支持向量机和遗传算法的优化方法，对钛合金铣削工艺参数进行了优化；结果表明，该方法准确、高效、可行，为钛合金加工工艺参数优化提供一种新的思路，具有良好的推广价值。

钛合金；正交设计；支持向量机；遗传算法

0 引言

钛合金材料具有抗高温、高强度、耐磨性好、抗腐蚀性能好等优良特性，广泛应用到航空航天、汽车、铁路交通、化工、石油、医疗等领域[1]。同时钛合金材料具有弹性模量小、导热性差和加工硬化严重差等特点，属于难加工材料，因此研究钛合金加工尤其是铣削加工性能，优化加工工艺参数，对提高加工效率和控制质量，降低制造成本，促进钛合金应用具有重要的实际意义。

目前，国内外很多学者对钛合金高速铣削工艺参数优化作出了大量的研究， Andre F.H.L等人[2]以加工效益作为优化目标，采用遗传算法求解的方法对铣削参数进行优化研究。Sardifias R.Q等学者[3]以切削力、表面粗糙度和加工成本为优化目标，建立多目标优化模型，对铣削加工参数进行优化研究。国内学者时政博等[4]以提高刀具寿命和加工效率为目标，通过预测铣齿功率大小和在线监控机床振动稳定性方法对切削参数进行优化。王明海等[5]提出了采用改进遗传算法寻优，以机床、刀具、工件等参量及所建立的切削力、刀具磨损和表面粗糙度非线性数学模型为约束条件，以最大生产率为目标的方法，实现了铣削用量优化。陈建玲等[6]提出以生产效率最大和刀具寿命消耗率最小为目标，建立了铣削参数多目标优化模型，采用扩展非支配排序遗传算法获得满意的Pareto解集，工程人员可根据实际需要灵活选取铣削参数。目前的优化方法大多是采用经验公式作为优化函数，少数也采用响应面法或神经网络模型预测法，均存在模型精度不足的问题，存在得到可能是局部优化解等缺点。

支持向量机是建立在统计学Vapnik-Chervonenkis(VC)维理论和结构风险最小原理基础上，用于解决小样本、强非线性、高维数、局部极小点等非参数回归建模问题的有效方法[7]，具有很强的泛化能力。大量事例表明，支持向量机比常用的响应面、Kriging模型和神经网络模型具有更好的回归性能[8-9]。

本文首先建立准确的钛合金铣削加工有限元计算模型，结合试验设计方法构建了切削力支持向量机预测模型，在预测模型的基础上建立以材料去除率为目标的优化模型，采用遗传算法求优的铣削工艺参数优化研究。

1 钛合金铣削加工有限元分析

在构建钛合金有限元计算模型时，一般选择Johnson -Cook模型作为本构模型，因为Johnson- Cook 模型是一种应用于大应变、高应变速率、高温变形的本构模型，应用于各种晶体结构材料时具有很好效果。首先建立正交切削有限元几何模型，这里取钛合金材料尺寸长50mm，宽20mm，刀具前角为10°，后角为6°，切削刃钝圆半径为0.001 mm，材料特性参数中，密度4.45g/cm3、弹性模量103GPa、热传导系数6.8W/m·K、比热容611J/kg·K、泊松比0.3，刀具假定为刚体。建立的钛合金有限元计算模型如图1所示。

通过计算分析，得到了给定的切削参数下切削力随时间的变化曲线如图2所示，可以看出切削过程在初始阶段切削力增加幅度大，随后进入塑性切削，切削力很快趋于稳定，由于节点不断分离，切削力不断出现小范围波动，我们取稳定后的平均值作为切削力。

图1 钛合金有限元分析模型

图2 时间—切削力变化

2 切削力预测模型构建

要构建钛合金切削参数与切削力支持向量机代理模型，首先进行切削参数分析，确定影响切削力的主要切削参数，采用实验设计方法进行样本布点，通过前述的有限元分析计算获得训练样本和检验样本；建立支持向量机回归模型；选取输入输出测试样本，判断模型的准确度，如不满足要求则继续增加样本重构模型。

2.1 试验设计

经大量研究和分析发现，影响在钛合金铣削过程中切削力大小的主要因素包括切削速度、铣削深度、每齿进给量和铣削宽度四个加工参数。为减少试验次数， 选用多因素正交试验设计方法进行样本步点，采用L16(44)正交表进行试验，采用有限元计算方法得到16组数据作为构建代理模型的训练样本，如表1所示。

表1 训练样本

2.2 支持向量机切削力模型构建

支持向量机用于回归算法时，其基本理论算法是给定样本集D={(xi,yi)|i=1,2,…,l}，其中xi∈Rn为n维输入样本，yi∈R为输出样本，通过非线性映射将xi∈Rn映射到高维特征空间，并在特征空间用回归函数f(x)=w·x+b拟合训练样本输入与输出之间关系。

利用函数的最优化方法，得到的支持向量机拟合函数为：

(1)

其中,K(xi,xj)=φ(xi)φ(xj)表示核函数，高维特征空间用核函数替代线性问题中的内积运算，选用径向基核作为支持向量机核函数，因为径向基核在多数情况下具有较好回归效果。

采用MATLAB软件，将训练样本对支持向量机进行学习，并进行检验， 通过建立的支持向量机模型的切削力预测值与试验值进行对比，切削力预测值与试验值对比曲线如图3所示。

图3可看出试验值和SVM模型预测值结果变化趋势一致，为了说明支持向量机模型的准确度，采用同样的样本对BP神经网络模型进行训练，获得BPNN模型切削力预测值与试验值对比曲线如图4所示。由图可知，构建的SVM模型预测值与试验值吻合效果明显要比BPNN模型好得多，这主要是由于小样本情况下SVM比BPNN的逼近精度好，当样本数量较多时，BPNN也具有很好的逼近精度。

表2为SVM模型预测值与BPNN模型预测值与试验值的对比表，可以看出SVM模型相对误差在5%以内，而BPNN模型某些局部预测值的相对误差很大，说明在小样本，高维情况下建立的基于SVM切削力预测模型精度更高、更有效。

图3 SVM切削力预测值与试验值对比曲线

图4 BPNN切削力预测值与试验值对比曲线

表2 试验值、SVM模型预测值与BPNN模型预测值对比表

3 基于SVM的铣削加工参数优化

3.1 SVM-GA优化算法流程

在钛合金铣削加工过程中，对于切削用量的选择受到很多条件的影响，若采用以往的参数优化方法，不但计算时间长，还可能只能得到局部优化解，得不到整体的优化解。本文采用支持向量机预测模型替代传统优化函数的基础上，以材料去除率为优化的目标建立优化模型，并以应用较为广泛的遗传算法对优化模型求解的方法，即SVM-GA方法，其基本流程如图5所示。

(1)试验设计：筛选影响加工效率和加工质量的主要因素作为优化变量，选取试验设计方法，设计样本。

(2)进行实验或以数值模拟替代实验，获取样本。

(3)构建SVM预测模型：采用遗传算法获取最优的SVM参数，通过学习样本构造支持向量机预测模型。

(4)模型更新：若代理模型的逼近精度不满足要求，则增加新的训练样本，重新构建模型，直至模型精度达到要求。

(5)优化求解：采用遗传算法对基于支持向量机预测模型的优化问题在设计空间全局寻优。

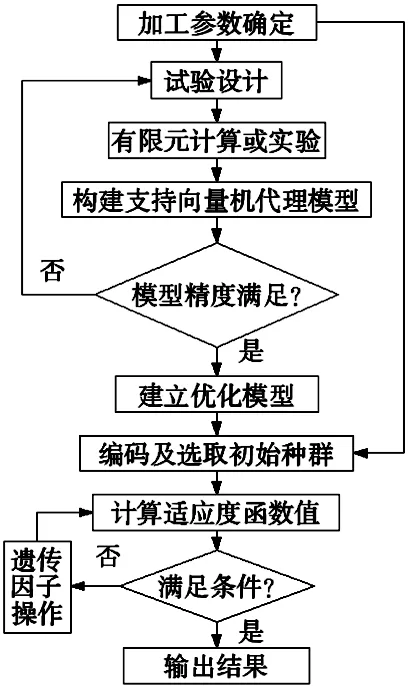
图5 SVM-GA优化算法流程图

3.2 基于SVM-GA铣削参数优化

钛合金铣削加工优化目标有材料去除率、加工效率、刀具寿命等，这都与加工参数有关。本文以材料去除率最小为目标函数，以切削力、刀具寿命、零件表面粗糙度和机床自身条件为约束函数，以切削速度、铣削深度、每齿进给量和铣削宽度四个加工参数为优化变量，以X表示，则优化模型表示为：

minF=f*(X)

(2)

利用GA进行优化，取种群数为120，交叉率0.5，变异率0.001，进行200代计算。

计算得到材料去除率最小的加工参数：切削速度为86m/min、铣削深度为0.92mm、每齿进给量为0.065m/mm、铣削宽度为12.6mm，将得到的SVM-GA算法优化结果作钛合金铣削试验和有限元计算，得到实际验证值，然后将SVM-GA算法优化结果与有限元验证结果进行对比，对比结果如表3所示，表中第4列为SVM-GA算法优化结果相对于有限元验证值的误差。

表3 SVM-GA算法优化结果验证

由表3可看出，本文采用的SVM-GA算法结果与实际测量准确验证相比，具有很高的计算精度，材料去除率、刀具寿命、零件表面粗糙度和切削力的相对误差均小于5.0%，实际应用中可以根据自身设备条件和工艺要求选择切削参数进行加工，因此，将SVM-GA算法应用到钛合金铣削加工参数优化具有很好的工程适用价值。

4 结论

本文提出了一种基于支持向量机预测模型和遗传算法的优化设计方法，通过试验设计和有限元计算生成训练样本，构建了具有优化参数功能的支持向量机预测模型，模型精度高，以预测模型替代优化模型的目标函数或约束函数，采用遗传算法对其优化模型求解。该算法用于解决钛合金铣削加工参数优化问题，结果表明，该方法准确、高效、可行。

以遗传算法作为优化器，具有全局收敛性，可处理无显式功能函数表达式、不可微、可行域不连通等问题，与支持向量机结合在一起，具有对优化初值敏感性低等优点。

有限元分析计算、样本布点设计、代理模型构建和遗传优化过程可实现完全分离，计算量小，为材料加工工艺参数优化提供一种新的思路，具有较好的推广价值。

[1] 艾兴，刘战强.高速切削加工技术[M].北京：国防工业出版社，2003.

[2] Andre F H L, Nivaldo L C, Elesandro A B, et al. Genetic Algorithm Applied to Investigate Cutting Process Parameters Influence on Workpiece Price Formation[J]. Material and Manufacturing Processes,2011,26(3):550-557.

[3] Sardifias R Q, Santana M R, Brindis E A. Genetic algorithm-based multi-objective optimization of cutting parameters in turning processes[J]. Engineering Applications of Artificial Intelligence, 2006,19(2):127-133.

[4] 时政博，黄筱调，丁文政. 基于自适应控制技术的铣削参数优化[J]. 组合机床与自动化加工技术，2012(4):105-107.

[5] 王明海，王京刚，郑耀辉,等.基于改进遗传算法的钛合金铣削参数优化[J].组合机床与自动化加工技术，2013(11):44-47.

[6] 陈建玲，孙杰，李剑峰.钛合金铣削加工参数多目标优化研究[J].中国机械工程，2014,25(2):169-173.

[7] Vapnik V N. Statistical learning theory[M]. New York: Springer, 1998.

[8] B Anirban, M Samy. Adaptive explicit decision functions for probabilistic design and optimization using support vector machines[J]. Comput Struct, 2008, 86(19):1904-1917.

[9] 王姣，刘海燕.基于支持向量机和遗传算法的刀具故障诊断[J]. 组合机床与自动化加工技术，2013(1):74-76.

ParametersOptimizationofTitaniumAlloyMillingProcessBasedonSupportVectorMachine

XIANG Guo-qi

(School of Resources and Environmental Engineering, Panzhihua University, Panzhihua Sichuan 617000, China)

Titanium alloys are widely used in various fields, the processing quality of this materials will be affected by the milling force. In order to guarantee the machining quality, improve production efficiency and reduce cost, the cutting parameters of the titanium alloy are reasonable selected, which plays an important role. In this paper, the Titanium Alloy milling process is analyzed by finite element method, a milling force prediction model was established based on Support Vector Machine(SVM), The design methodology based on (SVM) and genetic optimization(GA) is proposed for Titanium Alloy milling process parameters. The results show that this methodology is feasible and highly effective, and thus can be used in the machining process parameters optimum and other material processing fields.

titanium alloy; orthogonal experiment; SVM; genetic algorithm

TH166;TG506.1

A

(编辑李秀敏)