基于粒子群算法的倾斜度误差评定方法*
方 良,樊 军
(新疆大学 机械工程学院,乌鲁木齐 830047)
1001-2265(2017)10-0066-04
10.13462/j.cnki.mmtamt.2017.10.016
2016-12-23;
2017-02-14
国家自然科学基金-扭力冲击器双模射流自适应控制最佳匹配机理研究(11462021)
方良(1991—),男,安徽铜陵人,新疆大学硕士研究生,研究方向为高效钻井辅助工具研究,(E-mail)flechoer@hotmail.com;通讯作者:樊军(1965—),男,山东青岛人,新疆大学副教授,研究方向为高效钻井辅助工具研究,零件误差分析,(E-mail)xj_fanjun@163.com。
基于粒子群算法的倾斜度误差评定方法*
方 良,樊 军
(新疆大学 机械工程学院,乌鲁木齐 830047)
为了减小扭力冲击器关键部件冲击锤的倾斜度误差,根据倾斜度误差的国家标准,建立了符合最小区域条件的倾斜度误差评定模型。针对倾斜度误差的特点,提出一种惯性权重随实际情况动态变化的改进粒子群算法,从而对倾斜度误差进行评价,并给出了该改进算法的实现方法,最后将改进PSO算法与传统算法的计算精度进行比较。结果表明,改进的粒子群算法的计算精度比传统算法高,适用于扭力冲击器的倾斜度误差评定。
冲击锤冲击面;倾斜度误差;粒子群算法
0 引言
石油行业在经济发展中有着极其重要的地位,随着多年的开采钻探深度不断增加遇到的硬质岩层也越来越多,石油开采中常规钻井工具钻井速度低和钻井效率不高的缺陷越发明显。液动扭力冲击钻井方法是一种新型的钻井方法,其钻井速度快和效率高[1-6]。20世纪,俄罗斯工程师B·沃尔斯基最早开始液动扭力冲击工具的研制[2]。2000年,加拿大阿特拉公司研制了液动式和涡轮式扭力冲击器并成功投入商用[3];在国内,胜利油田研究院和中国石油大学联合研制了SLTIT型扭力冲击器,在一定程度上解决了我国石油钻井速度低和效率不高的问题,但是在实际应用中发现我国自主研发的扭力冲击器工作寿命不到20个小时,使得扭力冲击器难以在石油开采行业中得以广泛应用[4]。经研究发现其寿命低的主要问题在于其关键部件冲击锤的冲击面倾斜度精度难以保证。倾斜度误差并不是由工艺造成的,而是由冲锤加工完成后冲击面的倾斜度误差测量不准引起的。井下恶劣的工作环境及冲锤和锤座的高频碰撞对冲锤冲击面的倾斜度提出了较高的要求,倾斜度误差越大撞击过程中对锤座的应力就越大从而引起应力集中,严重影响了射流冲击装置的使用寿命和可靠性。目前最小区域法是评定面对面倾斜度误差的主要评定方法,用最小区域法评定倾斜度误差得到的误差值符合国标(GB1184-80),最小区域法先任意在待测量平面上随机选取一个测量点,然后对测量面上其它测量点依次测量和顺序处理,最后找出一个较小的区域[5],但这一算法在计算机上难以实现或运算周期较长。由于扭力冲击器倾斜度误差要求高,需采集大量的测量点,故最小区域法不适用于扭力冲击器关键部件倾斜度的测量。针对此问题,本文提出了一种适用于井下复杂工况要求的新型倾斜度测量方法,并将这一方法应用到扭力冲击器冲锤冲击面的倾斜度误差评定中。
1 冲击面倾斜度误差评定数学模型
扭力冲击装置依靠启动仓两侧的压差用定位套带动冲击锤转动,并利用定位套的惯性和射流元件的流道的自动切换功能实现其自动正反转,从而带动钻头往复的旋转[3]。扭力冲击器的模型如图1所示。

1.扭力冲击器锤座 2.冲击锤 3.定位套 4.轴承图1 扭力冲击器模型截面图
在评定定向误差时,必须先确定两个及多个被测要素之间的位置要求,而这里就需要选择与被测要素相对应的定位基准。基准是确定被测要素的方向或位置的前提,定位基准的作用是控制被测要素的公差带的位置和方向。根据定义,倾斜度是用来控制零件上被测要素相对于基准要素的方向偏离某一给定角度的程度[7-8]。如图2所示,本文给出了冲击锤基准平面示意图,这里倾斜度指的就是平面C相对基准平面A的倾斜度误差。
平面A:基准平面 平面B:理想平面 平面C:实际测量平面L:实际被测平面C与基准平面A的交线。

图2 冲锤基准平面示意图
设扭力冲击器关键部件冲击锤的基准平面A上测量点的坐标是pi=(xi,yi,zi),i=1,2,…n,其被测实际平面C上的测量点坐标是pj=(xj,yj,zj),j=1,2,…,n;
设最小区域条件下实际被测平面B的方程为:
z=px+qy+r
(1)
由条件可知基准平面A平面的方程为Z=0,故实际被测平面C与基准平面A的交线L方程为:
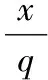
(2)
得出被测平面C与基准平面A交线L的方向向量是w(q,-p,0)。
基准平面A绕直线l旋转角度为θ可得L理想平面B,计算平面B的旋转矩阵M如下:


(3)
倾斜度误差等于被测平面C上任意一点pj=(xj,yj,zj),j=1,2,…,n到平面B的最大距离减去最小距离。
f=dmax-dmin
(4)
其中,d为点到平面的距离:

(5)
任选被测平面C上任一点pj=(xj,yj,zj),j=1,2,…,n。根据公式(5)计算,获得最大距离和最小距离,随后再根据公式(4)即可得到被测实际平面相对于基准平面的倾斜度误差[8]。
2 改进的基本粒子群算法
2.1 基本粒子群算法
PSO算法把粒子群中众多粒子看成是其优化问题的众多解,单个粒子也就是所有有解中的一个,每个粒子都由优化函数确定(适应值)。速度是矢量,粒子的运动速度就确定了粒子的速度大小和方向。每个粒子记得自己运动过的最佳位置Pbest(最逼近最优解的位置)这一点可以认为是粒子的学习经验;另外单个粒子还知道粒子群中其他粒子运动过程中发现的最佳位置gbest。Pbest和gbest为粒子下一步的运动提供了参考和指导[9]。具体来说,粒子群算法对粒子群中的众多粒子随机赋予位置和速度,粒子在运动过程中不断搜寻。其速度为Vi=(vi,1,vi,2…vi,n);其位置为Xi=(xi,1,xi,2…xi,n),粒子在其运动过程最佳位置Pbest和粒子群中所有粒子经历过的最佳位置gbest来更新自己的位置,只要粒子未达到停止条件就会一直继续搜索下去直到达到最终的最佳位置[9]。
下面给出了粒子运动过程中粒子运动速度的表达式和其运动位置的表达式,其中运动速度如下式:
vi,d(n+1)=ωvi.d(n)+c{r1[pbesti,d-xi,d(n)]+
r2[gbesti,d-xi,d(n)]}
(6)
运动位置如下式:
xi,d(n+1)=xi,d(n)+vi,d(n+1)
(7)
其中,ω:惯性权重;c:学习因子;r1,r2为[0,1]上的随机数。
2.2 改进的粒子群算法
在众多的优化算法中大多数算法都会出现早熟收敛问题,PSO算法也不可避免地出现了这一问题,最初提出的PSO算法的基本形式中并没有速度因子(惯性权重)w,在基本的PSO算法提出后,各行各业越来越多研究者发现粒子群算法存在着容易出现“早熟”这一问题,导致该算法过早的收敛,从而得到的解并非满足粒子个体最优解Pbest和全局最优解gbest的最佳位置[10]。PSO算法的改进形式中,起到关键控制作用的因素是算法中的惯性权重。在基本PSO算法中惯性权重w=1,这里w应按实际需要取合适的值,侧重于局部搜索时惯性权重应取较小的值;侧重于全局搜索时惯性权重应取较大的值,从而使得粒子的种群多样性得以提高。如果粒子群中全部粒子的惯性权重都相同,就造成了全局搜索和局部搜索之间的难以平衡,故这里提出对于粒子群中每个粒子的惯性权重应根据实际需要取值各不相同。粒子到Pbest的距离较近的找到Pbest的可能性更大,对于这样的粒子应该侧重于局部搜索也就是赋予它较小的惯性权重,同时聚焦距离变化率越大;相反,粒子到Pbest的距离较远的找到Pbest的可能性偏小,对于这样的粒子应该偏重于全局搜索也就是赋予它较大的惯性权重。同时粒子进化速度也会对惯性权重产生影响,惯性权重应随进化速度的改变做出相应的变化。据以上关于惯性权重的分析可知惯性权重应该为一个非线性递减的函数,这里提出以下自适应的非线性惯性权重递减的函数,公式如下:
(8)
式中,a1=0.3,a2=0.2,r为一个在[0,1]上的随机数。
这一对惯性权重的计算方法使得惯性权重随着聚焦距离变化率的变化不断的自我调整,使惯性权重的取值更加符合实际情况,平衡了全局搜索和局部搜索的需要,能使改进的PSO的计算精度取得很大程度上的提高。分析可知,当聚焦距离变化率较大时,最大聚焦距离和平均聚焦距离的差异越大,此时粒子群中粒子的全局搜索能力不足,故需要按照公式(8)来调整惯性权重以提高粒子的全局搜索能力;反之,当聚焦距离变化率较小时,最大聚焦距离和平局聚焦距离的差异越小,此时粒子群中粒子所谓局部搜索能力不足,故按照公式(8)来调整惯性权重以提高粒子的局部搜索能力。
该算法基本实现步骤主要为:
(1) 初始化:在粒子开始搜索前给粒子赋予起始速度Vi=(vi,1,vi,2…vi,n)和给定起始坐标位置Xi=(xi,1,xi,2…xi,n);
(2) 评价:计算粒子的适用值;
(3) 个体更新:比较粒子当前的适用值与Pbest,如当前粒子的适用值优于Pbest,则用当前的适应度值作为Pbest;
(4) 全局更新:比较粒子当前的适用值与gbest,如当前粒子的适用值优于gbest,则用当前粒子适应度值作为其gbest[10];
(5) 更新粒子:计算粒子的聚焦距离变化率并确定惯性权重,首先重新计算粒子群中所有粒子的速度,同时重新计算粒子群中所有粒子的位置;若粒子超过迭代次数的最大值或者符合最小准则,则终止程序,否则跳转到第2步。
(6)停止条件:满足最小停止条件则程序结束;否则,回到第2步,重新开始程序。Pbest:粒子在搜索过程中经历过的最好位置的适应值;gbest:粒子群中所有粒子经历过的最佳位置的适应值。
3 实例验证与结果讨论
根据传统测量方法来测量被测平面C与基准平面A的倾斜度误差,这里使基准平面A与水平面平行,将扭力冲击器关键部件冲击锤放在预制的工装上,将样件放置在冲击锤上,样件上表面安装了测量装置,如图3所示。传统的测量方法虽然简单易行但是其操作繁琐,容易受人为测量不稳定性的影响,从而使得测量精度相对较低[11-12]。

图3 传统测量方法示意图
扭力冲击器设计要求冲锤冲击面相对基准平面的倾斜度误差为0.09mm。先创建测量坐标系然后测各个点的坐标,记录各个测量点的数据并录入测量系统。据文献[1-6],冲锤与基准平面的理论正确角度为23°,三坐标测量设备测量所得的冲击面对基准平面倾斜度数据,如表1所示。
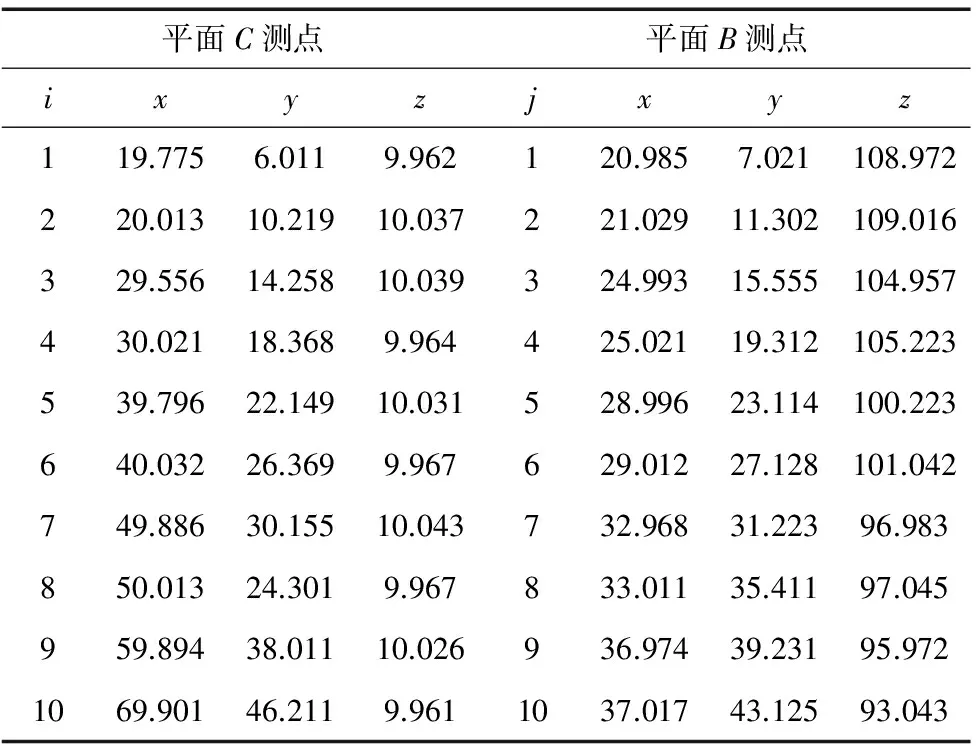
表1 被测零件倾斜度测量数据(单位:mm)
3.1 基准平面的确定
根据具体问题,PSO算法的参数设计如下:粒子规模或粒子数N:通常取值区间为[10,40],根据实际令粒子数为20;粒子维数D:粒子在空间内的搜索维数或实际问题解的长度,根据实际取粒子维数为4;粒子速度:Vmax=0.02;惯性权重:w=0.5;最大迭代次数:M=1000;学习因子:c=2.0。
根据测量的数据评估或者最小二乘法计算确定最小二乘平面的值为:a=0.0074,b=-0.009,c=9.918。
3.2 倾斜度误差计算
将被测点pj(xj,yj,zj)j=1,2,3,…,n代入公式(3)经过坐标变换得到拟合平面,再利用公式(5)、式(4)可求得该测量平面的倾斜度误差。
根据上文分析的优化算法将数据比较得知:传统的打表测量方法倾斜度误差值为f传统=0.095,基本的PSO算法计算冲击面对基准平面的倾斜度误差值fpso=0.089,改进的PSO算法计算冲击面对基准平面的倾斜度误差值fDcwpso=0.083。

表2 各评定方法误差值比较(单位:mm)
零件图纸中倾斜度的公差为0.090,若按照传统方法测量可能造成误判,将本来合格的零件当成不合格的零件,将给工业生产带来一定的经济损失。基本的粒子群算法和改进的粒子群算法相比较,虽然两种算法得出的倾斜度误差均符合要求,改进的粒子群算法的计算精度优于基本的粒子群算法。
4 结束语
本文根据扭力冲击器在石油行业应用中存在的问题,提出了通过用改进的粒子群算法处理误差测量数据以减小了冲击锤冲击面倾斜度误差。建立了面对面倾斜度的数学模型,提出了一种动态改变惯性权重的新型粒子群算法,并将扭力冲击器上关键部件的倾斜度要求作为实例分别计算并比较两种算法计算的倾斜度误差,得到了不错的效果。改进的粒子群算法原理简单,计算效率和准确度高,相比基本粒子群算法更能有效准确的评价零件的倾斜度误差,特别适合扭力冲击器这一新型冲击辅助装置。同时,该方法同样适用于其他形位公差(平面度,垂直度,直线度等等)的评定,对形位公差的评定具有一定的参考价值。
[1] 李伟涛.液动锤射流元件工作寿命试验研究[D]. 长春:吉林大学,2004.
[2] 菅志军,张玉霖,王茂森,等.冲击旋转钻进技术新发展[J].地质与勘探,2003(3):78-83.
[3] UNITED DIAMOND LTD. Rotational impact drill assembly.[P] United States.E21B4/10. US2002166700 A1. 2002-11-14.
[4] 陈劲松,翟应虎.SYZJ型冲击动载发生器的设计理论及方法[J].石油钻探技术,2000,28(6):34-35.
[5] 李学军,常智勇,莫蓉,等.基于遗传算法的圆柱几何特征信息的测量[J].计算机工程与应用,2006,42(22):56-58.
[6] 蒋龙,樊军.脉动扭转冲击装置结构设计及动力仿真[J].机械设计与制造,2015(12):12-15.
[7] 罗均,王强,付丽.改进蜂群算法在平面度误差评定中的应用[J].光学精密工程,2012,20(2):422-430.
[8] 张静.基于新一代GPS的定向误差评定方法的研究[D].桂林:桂林电子科技大学,2011.
[9] 茅健,郑华文,曹衍龙,等.基于粒了群算法的圆柱度误差评定方法[J].农业机械学报,2007,38(2): 146-149.
[10] 毛汝君,徐蔚鸿.基于粒子群-蚁群混合算法的软件测试数据生成方法研究[J].硅谷,2013(1):91-93.
[11] 孙华平,王京,胡仲勋.基于UG/Open GRIP的面对面倾斜度误差的处理和评定[J].图学学报,2008,29(1):158-161.
[12] 喻晓,彭建喜,刘建萍.基于改进粒子群算法的圆柱度误差评定[J].微型机与应用,2011,30(15):74-77.
InclinationErrorsEvaluationMethodBasedonParticleSwarmOptimization
FANG Liang, FAN Jun
(School of Mechanical Engineering, Xinjiang University, Urumqi 830047, China)
In order to reduce the inclination error of the impact hammer of the key component of the torque impactor, according to the national standard of inclination error, the model of inclination error evaluation was established according to the minimum region condition. According to the characteristics of the inclination error, an improved particle swarm algorithm that inertia weight with the actual dynamic changes is proposed. So the inclination error is evaluated and the improved algorithm is given. Finally the calculation precision of the improved PSO algorithm and traditional algorithm are compared. The results show that the improved particle swarm optimization algorithm is more accurate than the traditional algorithm and is suitable for the evaluation of the inclination error of the torque impactor.
hammer impact surface; inclination error; particle swarm optimization
TH16;TG113
A
(编辑李秀敏)

