深圳铜鼓航道失控船舶对海底管道风险分析
赵仓龙, 冯爱国
(1.上海海事大学 商船学院, 上海 201306; 2.南通航运职业技术学院 航海系, 江苏 南通 226010)
深圳铜鼓航道失控船舶对海底管道风险分析
赵仓龙1,2, 冯爱国2
(1.上海海事大学 商船学院, 上海 201306; 2.南通航运职业技术学院 航海系, 江苏 南通 226010)
我国西气东输二线管道工程中的管线工程穿越深圳铜鼓航道,该航道交通流密度大,航道中的船舶一旦在管线附近失控,将对海底管线构成较大的威胁。对此,通过构建船舶失控漂移计算模型,就铜鼓航道中对海底管线构成威胁的危险失控区域进行计算分析,得出海底管线附近水域危险失控区域范围。分析结果可为铜鼓航道中的失控船舶采取有效措施免除对海底管道造成影响提供科学依据和参考。
水路运输;海底管道;失控;失控漂移模型
Abstract: The West-East pipeline project Ⅱ, one of the national energy strategic project, is laying the pipeline through the Tonggu waterway at west of Shenzhen. Tonggu waterway is the traffic hub for large ships to visit the Shenzhen western port and have a traffic flow of high density. Once a ship near the pipeline is out of control, the safety of the submarine pipeline will be under risk. A drift model for the ships out of control is set up and the area where those ships may endanger the seabed pipeline is calculated. This study can assist the ships out of control to decide whether to take tugs to assist braking or other appropriate measures from angle of pipeline safety.
Keywords: waterway transportation; submarine pipeline; out of control; drift model for ship out of control
西气东输二线管道工程是我国能源战略的重点工程,由新疆的霍尔果斯向东延伸至上海,向南延伸至广州。西气东输二线海底管道工程作为西气东输二线管道工程中的重要组成部分,是我国目前海底管道口径最大的管道工程,设计年输气量60亿m3,可促成多气源安全供应格局,充分保障我国地区经济社会发展对天然气的需求。
西气东输二线海底管道始于深圳市大铲岛西北侧水域,穿越大铲水道、矾石浅滩及铜鼓航道,延伸至香港龙鼓滩输气站。铜鼓航道作为深圳西部水域航行环境最复杂的航道,是大型船舶进出深圳西部港区的必经航道(见图1)。该航道中的船舶一旦在管线附近失控,将对海底管线构成较大的威胁。因此,通过对船舶失控漂移建立计算模型,就铜鼓航道中船舶失控对海底管线造成的危险进行风险分析,得出海底管线附近水域危险失控区域范围,对铜鼓航道中的失控船舶采取措施避免对海底管道造成影响提供科学依据和参考。
1 船舶失控漂移运动模型


图1 西气东输二线海底管道路由

图2 船舶失控漂移动态示意
1.1冲程和冲时的计算[3-7]
1) 失控时的船速(υ0)是指船舶在失控开始时的船速,其计算式为

(1)
式(1)中:V为船舶失控开始时的航速,m/s;U为船舶失控开始时的流速,m/s;α为船舶失控时艏向与航道主轴向的夹角,(°);β为舶舶失控时水流流向与航道主轴向的夹角,(°)。
2) 冲时(T)是指失控船舶自失控点开始直至惯性消失所用的时间,其计算式为
T=-Tstlnv/v0
(2)
式(2)中:υ为失控船舶在冲程时间内任意时刻的航速,m/s;υ0为船舶失控开始时的航速,m/s;Tst为失控船舶的减速时间常数,Tst=c/ln 2,c可根据船舶排水量查表1获得。

表1 船速减半时间常数c
3) 静水冲程(S′)是指失控船舶在冲时T沿运动方向继续移动的距离,其计算式为

(3)
4) 动水冲程(S)是指失控船舶在冲时T内随流漂航的距离,在计算动力冲程时应予以考虑,其计算式为
S=υ0Tst(1-e-T/Tst)+UTcos(β-α)
(4)
5) 冲距(Sc)是指动水冲程在y轴上的投影,其计算式为
Sc=υ0Tst(1-e-T/Tst)cosα+UTcosβ
(5)
6) 漂距(SP)是指失控船舶在惯性力完全消失后在流的作用下继续沿航道方向漂移的距离,其计算式为
Sp=Utpcosβ=(Dsk-Sc)
(6)
tp=Sp/Ucosβ=(Dsk-Sc)/Ucosβ
(7)
式(6)和式(7)中:tp为失控船舶流淌漂移时间,s;Dsk为失控点与海底管线之间沿y轴方向的距离,m。
1.2漂移量的计算[8-13]
1.2.1流致漂移量的计算
(1) 冲期内流致漂移量(B1)是指失控船舶在整个冲时T内在流的作用下沿x轴向南偏移的距离,其计算式为
B1=υ0Tst(1-e-T/Tst)sinα+UTsinβ
(8)
(2) 流淌漂移量(B2)是指失控船舶在惯性消失后继续受流的作用到达海底管线工程水域时在x轴方向上移动的距离,其计算式为
B2=Utpsinβ=Sptanβ
(9)
(3) 冲期到达海底管线工程点前流致漂移量(B3)是指失控船舶在冲距大于失控点至海底管线工程点的距离时(即Sc>Dsk)在流的作用下自失控点到达海底管线工程水域过程中(工程点前冲距为Dsk)在x轴方向上移动的距离,其计算式为
B3=υ0Tst(1-e-t/Tst)sinα+Utsinβ
(10)
式(10)中:t为失控船舶自失控点受流的作用到达海底管线水域处所需的时间,其计算式为
Dsk=υ0Tst(1-e-t/Tst)cosα+Utcosβ
(11)
1.2.2风致漂移量的计算
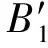
(12)
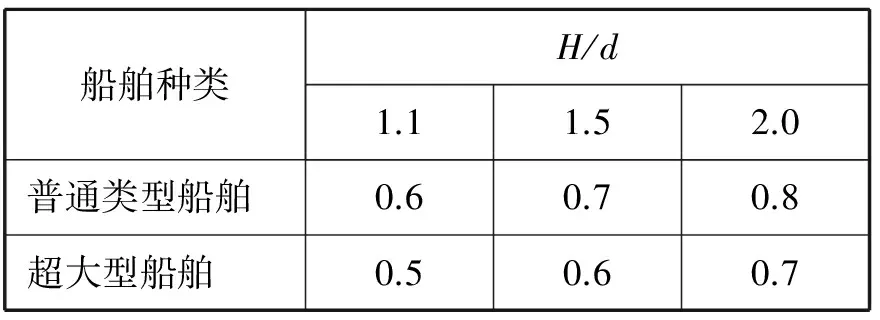
表2 浅水水域横风漂移速度的修正系数K′

(13)

(14)
式(14)中:υa3为冲期海底管线工程点前的风中船速(取失控船舶在风的作用下的平均航速),kn;Va3为冲期相对风速,m/s;t为失控船舶从失控点到达海底管线工程点所需的时间。
1.3总漂移量计算
总漂移量(B)是指失控船舶在偏航、风和流等主要影响因素的共同作用下从失控点漂移到海底管道工程点沿x轴方向漂移的总距离。其大小是衡量失控船舶失控后是否会给海底管道工程带来危险的重要依据之一。
1) 当Dsk>Sc时,失控船舶的惯性在船舶到达海底管线工程点之前就已消失,失控船舶将在流的作用下淌航一段距离后到达海底管线工程点。该情况下失控船舶的总漂移量和所需时间分别为
2) 当Dsk (17) 2.1航行条件分析 铜鼓航道是深圳西部港区的第2条深水航道,目前的建设规模可满足8 000 TEU集装箱船全天候单向通航。铜鼓航道工程航道人工开挖段长23.7 km,有效宽度210 m,通航水深15.8 m,设计底标高-15.8 m。基于此,模型计算中选取8 000 TEU集装箱船作为代表船型。船型尺度为:船长347 m,船宽43 m,满载吃水14.5 m。 赤湾站的常风向为东,频率为23.38%;次常风向为东南,频率为14.23%。强风向为东南,最大风速为30 m/s;风力>7级的风年出现频率为0.54%。赤腊角站的常风向为东,年出现频率为41.37%;次常风向为北,年出现频率为12.66%;强风向为东;风力>7级的风年出现频率为1.03%。 受巴士海峡传入的太平洋潮波的控制,珠江口的潮流属于不规则的半日潮混合潮流,其涨落潮历时不等现象较明显,涨潮历时从外海向内递减。选择铜鼓航道断面东部、中部和西部3个点位进行洪季涨落潮的测量,具体数据见表3和表4。 2.2研究工况分析 利用船舶失控漂移运动模型计算出不同冲距下的时间、航速、漂移量等船舶失控后的相关数据,根据这些数据确定船舶失控后可能给管道带来危险的区域。船舶漂移坐标系示意见图3。 表3 铜鼓航道洪季大潮涨落急条件下的流速 表4 铜鼓航道洪季小潮涨落急条件下的流速 图3 船舶漂移坐标系示意 根据气象水文资料及研究工况,若常风向取分析工况方向(Vc为水流速度,Vw为风速,Vs为航速),则对海底管道威胁最大的工况即为图示的工况。船舶在O点失控后,水流、风和偏航共同把船舶推向管线附近。 由于铜鼓航道水流方向基本上与航道中心线的走向一致,因此若假设船舶失控前在中心线附近航行,失控后受风、流的影响漂移到距离航道边界约100 m处,则在船舶漂航到管线前,偏移量达100 m时恰巧到达海底管线水域,船舶失控点所在的水域是对管线有危险的区域。若偏移量很小,则船舶可漂过管线;若偏移量太大,则在漂移到管线前已搁浅,对管线没有威胁。这里选取漂移量分别达到50 m,100 m和150 m等3种情况来分析铜鼓航道典型船舶(8 000 EU集装箱船,船型尺度为:船长346 m,型宽45.6 m,型深24.8 m,满载吃水14.5 m)在不同工况下的时间和冲程。 依据铜鼓航道东线段的水流和风的基本概况,航道轴线与水流的最大夹角为30°,航道轴线与风的最大夹角为74°。因此,选取分析工况: 1) 流速0.4 m/s和1.4 m/s。 2) 风速取无风、4级和8级。 3) 航速12 kn,取铜鼓航道集装箱船失控前正常进出港航速。 3.1危险失控区域计算 根据模型计算方法,确定该集装箱船在不同环境条件下的危险失控区域(失控点坐标为(x,y),x指漂移量或失控点与航道边界间的距离,y指失控点与海底管线间的距离)。有关危险失控区域分析数据见表5,其中“无风”表示风速<2级,或风对船舶的“冲程”和“漂移量”的作用很小。 根据船舶失控漂移运动模型,船舶一旦在铜鼓航道中失控,在风、流的作用下漂移到航道边界,将会搁浅。若正好在海底管线上方搁浅,则会对海底管线构成较大的威胁。通过上述计算,得出船舶在海底管线两侧水域内失控时对海底管线构成影响的危险失控点(见表5)。 3.2危险性分析 船舶一旦在铜鼓航道失控漂移至管线附近,横向偏移量将会向航道两侧偏移约105 m。若船舶在到达管线前方水域时就已航行到铜鼓航道边界,则会搁浅,对管线已无影响。通过计算分析上述失控漂移模型及总结表5中的数据可知,船舶失控后能漂移到管线附近的危险区域有以下特点: 1) 在海况较好、无风顺流的情况下,当流速为0.4 m/s时,船舶在3 000~4 000 m内能漂航到管线附近;当流速为1.4 m/s时,船舶在7 000~9 000 m内能漂航到管线附近。在其他距离情况下,若失控前在航道中心线附近航行,且偏航角<3°,则不抛锚可漂航过管线,不会搁浅;逆流时超过3 000 m则开始倒退。 2) 在风速达到4级左右,流速为0.4 m/s时,船舶在2 000~8 000 m内能漂航到管线附近;当流速为1.4 m/s时,船舶在2 000~4 000 m内能漂航到管线附近。在其他距离情况下,若失控前在航道中心线附近航行,且偏航角<3°,则不抛锚可漂航过管线,不会搁浅;逆流时超过5 600 m则开始倒退。 表5 10万吨级集装箱船危险失控区域分析 3) 在风速达到8级左右,流速为0.4 m/s或1.4 m/s时,船舶在1 000~3000 m内能漂航到管线附近。在其他距离情况下,若失控前航行至航道中心线附近,且偏航角<3°,则不抛锚可漂航过管线,不会搁浅;逆流时超过4 200 m则开始倒退。 综合考虑,船舶在管线两端5 000 m范围内失控都有漂移到管线附近上方搁浅的危险。当失控距离>5 000 m时,建议采用拖船施救。 经船舶失控漂移运动模型综合计算分析,得到8 000 TEU集装箱船在铜鼓航道中心线航行过程中失控后的漂移数据。对这些数据进行分析可知:若失控船舶在管线两端>5 000 m范围内失控,则由于失控距离较远,留给救援部门的时间较长,建议采用拖船对失控船舶进行施救(制动),进而避免失控船舶向海地管线方向漂移;若失控船舶在管线两端5 000 m范围内失控,则漂移到管线附近上方搁浅的概率较大,建议业主与相关部门配合在管线两侧各2 n mile处设置警示标志。 由于铜鼓航道有效航宽较小,因此应对大型船舶实行单向通航的管理措施,在进入警示水域前调整好航向,采用适当的风、流压角(一般为3°~5°);同时,采用一定挂高量的方法,挂高量在航道中心线受风、流侧30~50 m。若在海底管线构成影响的危险失控点水域发生船舶失控情况,则及时启动船舶失控应急预案,与海事交管部门联系采取进一步的制动措施(如抛锚制动、拖船协助制动等)。后续将对船舶抛锚制动进行研究,分析船舶失控后采取抛单锚、双锚措施所对应的船舶失控冲程,进而为失控船舶驾引人员操纵船舶提供科学依据和参考。 [1] 薛满福,杲庆林.船舶操纵与避碰(船舶操纵) [M].北京:人民交通出版社,2012. [2] 王宏明.船舶抛锚对渤海湾海底管道撞击影响[J].中国航海,2015,38(2):56-59. [3] 张磊.基于船舶应急抛锚的海底管道埋深及保护研究[D].武汉:武汉理工大学,2013. [4] 甘浪雄,喻晓,高国章.船舶失控应急的港珠澳大桥桥区水域尺度[J].中国航海,2011,34(4):76-80. [5] 王杰,肖菲,王爱民.海底管线防护系统的设计与实现[J].中国航海,2015,38(3):75-78. [6] 丁天明,艾万政.渔船在流场中失控漂移预报模型[J].水运管理,2015,37(10):14-16. [7] 母德伟,刘明俊,韩述,等.船舶失控漂移模型在重庆白居寺长江大桥通航安全影响论证中的应用研究[J].交通科技,2014(5):155-158. [8] 白俊磊.海底管道坠物碰撞损伤数值模拟分析研究[D].大连:大连理工大学,2013. [9] 丁红岩,乐丛欢,张浦阳.落物撞击作用下海底管道风险评估[J].海洋工程,2010,28(1):25-30. [10] 江福才,沈崇松.船舶失控漂移模型在防波堤水域的应用研究[J].船海工程,2009,38(3):172-175. [11] 朱倩.海底管线系统的风险评估技术研究[D].大连:大连理工大学,2013. [12] 宋俊强,陈昆,霍知亮,等.围海造陆工程对海底管线的影响及防护方案的研究[J].水利学报,2015,46(S1):153-157. [13] 丁鹏.海底管线安全可靠性及风险评价技术研究[D].青岛:中国石油大学,2008. [14] 李学东,耿杰哲,李学恩.基于锚泊活动的海底管线埋深研究[J].武汉理工大学学报(交通科学与工程版),2015,39(5):1021-1023. [15] 庄元,宋少桥.海底管线埋深问题研究[J].大连海事大学学报,2013,39(1):61-64. [16] 蓝天,余建星,张英,等.基于ABAQUUS的拖锚载荷对海底管线的影响研究[J].天津理工大学学报,2014,30(1):1-5. [17] 刘欢,冯梅芳,张文海. 抛锚作业撞击海底管道的影响分析[J].石油工程建设,2012,38(1):21-23. RiskAnalysisforSubmarinePipelineinCaseofShipOut-Of-ControlinShenzhenTongguWaterway ZHAOCanglong1,2,FENGAiguo2 (1. Merchant Marine College, Shanghai Maritime University, Shanghai 201306, China; 2. Department of Navigation, Nantong Shipping College, Nantong 226010, China) P756.2; U698 A 2016-10-11 江苏省交通科技项目(2011C04-2);2014年度江苏省第四期“333工程”科研资助立项项目(BRA2014312) 赵仓龙(1983—),男,江苏盐城人,讲师,博士生,从事水上交通环境与安全保障研究。E-mail: zhaocl@ntsc.edu.cn 1000-4653(2017)01-0064-05
2 失控船舶运动状态研究的基本条件
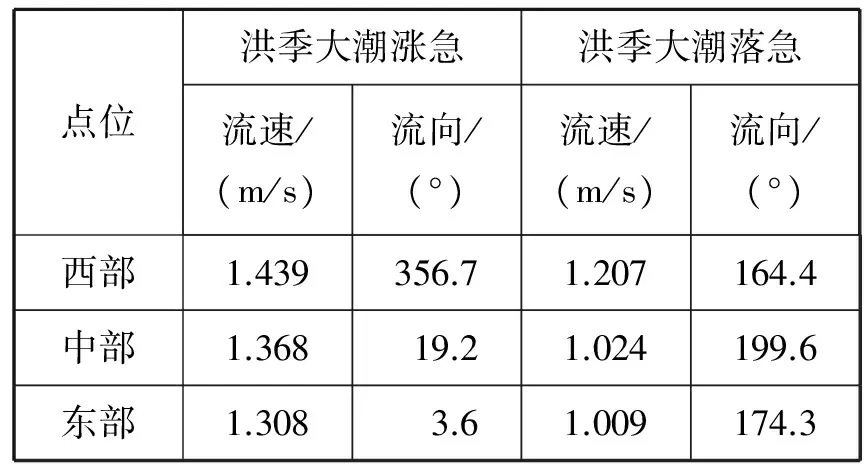
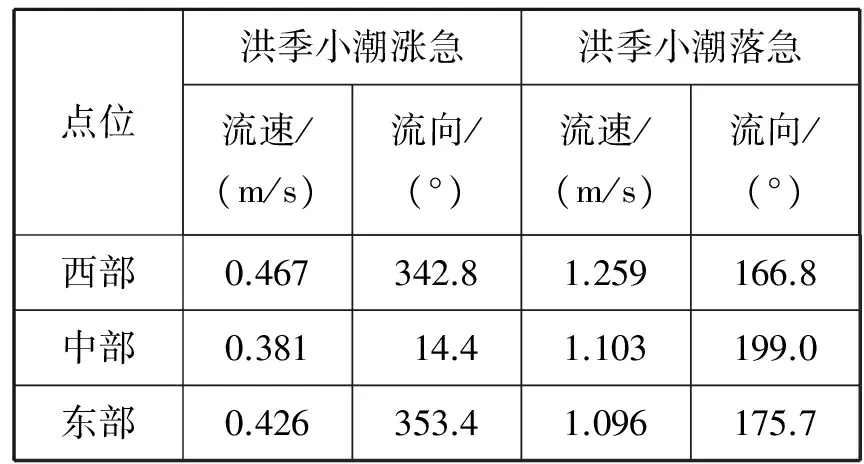

3 铜鼓航道失控船对海底管道危险性分析

4 结束语

