格密码技术近期研究进展
张平原 蒋 瀚 蔡 杰 王晨光 郑志华 徐秋亮
1(山东大学软件学院 济南 250101) 2(山东大学数学学院 济南 250100) 3(山东师范大学信息科学与工程学院 济南 250358) (pingyuan0802@163.com)
2017-08-31;
2017-09-11
国家自然科学基金项目(61572294);国家自然科学基金重点项目(61632020);山东大学基本科研业务费专项资金项目(2017JC019) This work was supported by the National Natural Science Foundation of China (61572294), the Key Program of National Natural Science Foundation of China (61632020), and the Fundamental Research Funds for Shandong University(2017JC019).
蒋瀚(jianghan@sdu.edu.cn);徐秋亮(xql@sdu.edu.cn)
格密码技术近期研究进展
张平原1,2蒋 瀚1蔡 杰1,2王晨光1,2郑志华3徐秋亮1
1(山东大学软件学院 济南 250101)2(山东大学数学学院 济南 250100)3(山东师范大学信息科学与工程学院 济南 250358) (pingyuan0802@163.com)
格理论最初是作为一种密码分析工具被引入到密码学中的,用于分析背包密码体制、RSA密码体制等.在1997年,Ajtai和Dwork第一次构造了一个基于格的密码体制Ajtai-Dwork,随后在1998年出现了NTRU密码体制.当时基于整数分解及离散对数的公钥密码体制是主流,格密码一直没有得到足够的重视.直到2009年,Gentry基于格密码构造了首个全同态密码方案,格密码才得到了广泛的发展.2015年,Peikert在“格密码十年”一文中,对之前格密码的发展做了一个很好的总结.同在2015年,美国国家标准和技术研究院(National Institute of Standards and Technology, NIST)发布了“后量子密码报告”,报告指出:由于量子计算技术的飞速发展,现有的公钥密码标准在量子计算下将不再安全.同时NIST在全球范围内展开了后量子密码算法标准的征集工作.格密码作为一类经典的抗量子密码,公认是后量子密码算法标准最有力的竞争者,近2年得到了飞速的发展,出现了许多优秀的研究成果.从基于格的零知识证明、格加密、格签名以及格密钥交换4个方面,对近2年格密码研究进行了总结,并对格密码的发展趋势进行了展望.
格密码;基于格的零知识证明;格加密;格签名;格密钥交换
格L是n维欧氏空间n中一个离散的加法子群.更直观地说,一个格L⊂n是一组基向量b1,b2,…,bn∈n的所有整系数线性组合的集合,也就是}.在格上存在着各种计算困难问题,一些经典的问题如最短向量问题(shortest vector problem, SVP)、最近向量问题(closest vector problem, CVP)以及这些问题的近似版本等.对应地,对这些困难问题存在着相应的近似解法,如LLL算法是最著名的求解近似SVP问题的算法[1].
格代数结构最早是作为一种密码分析工具被引入密码学的.早在1982年,Shamir首次利用了格理论对背包公钥密码算法进行了攻击[2];而在1996年,Coppersmith提出将破解RSA体制转化成求解格中困难问题[3], 进而利用LLL算法来求解.
利用格来设计密码体制要归于Ajtai的工作.在1996年,Ajtai[4]开创性地证明了格中某些困难问题如果在最坏情形(worst-case)下是困难的,那么它在平均情形(average-case)下也是困难的.这个结果表明,除非某种格问题的所有实例都容易解决,否则我们就有可能基于该问题构造安全的密码方案.因此,格密码可以提供基于worst-case困难下的安全性证明.1997年,Ajtai和Dwork构造了第一个格密码体制Ajtai-Dwork[5].随后出现了一批基于格的密码体制,其中比较著名的有NTRU密码体制[6],该体制对格密码的后续发展产生了深远影响.
由于基于大整数分解以及离散对数困难问题的密码体制,如RSA,DSA,ECC等是当时的主流公钥密码体制,基于格的密码体制没有得到广泛的关注.直到2009年,Gentry首次给出了基于格的全同态加密方案的构造[7],促成了格密码研究的一次热潮.全同态加密的概念虽然在1978年就由Rivest等人[8]提出,但30多年一直没有得到研究进展.Gentry的工作证明了全同态密码方案的存在性,同时带动了格密码的研究,2009年之后,在格的数学基础、格上困难问题、格密码体制的构造等方面出现了大量的工作.对这一期间的工作,也有一些综述文章进行了归纳总结.王小云等人的综述[9]主要侧重于对格的数学基础方面;而Peikert的综述[10]是一篇对截止到2015年格密码发展的一篇覆盖全面、逻辑清晰的工作.
在2015年,美国国家标准技术研究院(NIST)发布了一份后量子密码报告[11],对公钥密码算法的换代工作以及后量子子密码算法研究工作产生了极大的推动作用.事实上,早在1997年,Shor就提出了一种量子算法,可以在多项式时间内解决大整数分解问题[12],Shor算法的核心就是利用量子计算的性质来求出函数的周期,这种思想对于求解离散对数问题仍然有效.因此,Shor的工作表明,一旦量子计算机被真正制造出来,基于大整数分解问题,以及离散对数问题的密码体制,包括RSA,ECC等将不再安全.NIST的后量子密码报告强化了量子计算机出现的预期,同时NIST也开始在全球范围内开展后量子密码算法标准的征集工作.
NIST的后量子密码报告中提到的后量子密码算法主要有于基于格的密码(lattice-based crypto-graphy)、基于编码(code-based cryptosystems)的密码系统、多变量密码(multivariate cryptography)以及基于哈希算法的签名(Hash-based signatures)4种,此外,还有学者基于超奇异椭圆曲线上的同源问题,共轭搜索问题(conjugacy search problem)以及辫群(braid groups)中的相关问题等设计抗量子的密码系统等.在这些解决方案中,由于基于格可以设计加密、签名、密钥交换等各种密码系统,且具有较可信的安全性,因此格密码被公认是后量子密码算法标准最有力的竞争者.近几年来,格密码成为密码学领域最热门的研究方向之一,出现了大量的研究成果,因此有必要对近年来的成果做一个梳理.
本文按照基于格的零知识证明、格加密、格签名以及格密钥交换4个方面,总结了近2年来格密码的重要研究成果,并对格密码的研究趋势做出了展望.
1 格困难问题的算法和计算复杂性
给定一个格L,用λi(L)表示第i个逐次最小长度,即λi定义为以原点为球心,包含i个线性无关格向量的最小球的半径.
1) 最短向量问题(shortest vector problem, SVP).给定一个格L,找它的一个最短的非零格向量.
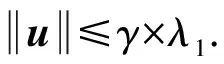
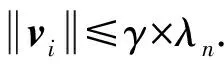
4) 判定版本SVP问题(GapSVP).给定一个格L和有理数r,确定是下列哪种情况成立:λ1≤r或者λ1≥γ×r.
5) SIS(small integer solutions)问题.给定矩阵A∈n×mq(m≥n)和实常数v,找一个非零向量u∈m,使得Au=0modq,且.它等价于在模格m:Au=0modq}中找一个向量长度不超过v的非零格向量.
6) LWE(learning with errors)问题.非正式地,LWE问题是指对于多个独立抽样(a,〈a,s〉+e)∈nq×q和(a,u)∈nq×q,它们是计算不可区分的,其中a,s←nq,u←q,e随机选区于一个“low-weight”的分.在一定意义下,它是SIS的对偶问题.定义模格Λq(A)={x∈m:x=ATymodq,y∈n},则LWE问题可以看作模格Λq(A)上的BDD(bounded distance decoding)问题.
为了提高格密码的效率,密码学家提出了一类具有额外代数结构的格—理想格[10],具体地说,f-理想格是对应于环[X]〈f〉的理想的一类格,其中f是首项系数为1的不可约多项式,如f=xn+1(n是2的幂次方).同样地,可以定义理想格上的ring-SIS和ring-LWE问题.
1.1格困难问题的求解算法
在经典计算理论下,密码学家在求解SVP和CVP的算法方面做出了许多贡献.求解格问题的最著名的方法是 Lenstra,Lenstra和Lovasz 在文献[3]中提出的LLL算法,该算法在多项式时间内能解决近似因子为2O(n)的SVP问题.尽管LLL算法的理论估计值较差,但在具体实现中却比理论要好一些,这个问题目前也没有合理的解释,该问题也是有待于进一步努力的方向,因为LLL算法的实际运行结果直接关系到格密码方案的安全参数选取,即影响密码方案的效率.
之后,许多密码学家对LLL算法进行了改进,其中包括Schnorr算法[13]、Schnorr和Euchner在1994年提出的BKZ算法[14]和Chen等人的BKZ 2.0算法[15],但至今为止,这些算法求解近似SVP问题都需要指数时间的复杂度,在多项式时间内仅能解决近似因子为2O(n lblb n/lb n)的SVP问题.因此可以猜想,不存在多项式时间算法能够解决近似因子为多项式的近似SVP问题,从而我们就可以用格来构造相应的密码学方案.
在量子计算理论下,自从Shor发现量子算法以来,传统的基于整数分解和离散对数的问题困难性受到了极大的威胁.自然地,是否也存在量子算法来求解格中困难问题,但目前为止还没有发现明显优于经典算法的量子算法用于求解格中的问题.因此,格密码在量子计算下仍能够保证方案的安全性.
1.2格困难问题的计算复杂性
对于一般格中的困难问题的计算复杂性,由于SIS和LWE能够归约到GapSVP和SIVP上去.因此,选取足够小的近似因子,一般格中的困难问题大都是NP-hard的[3].
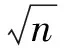
虽然理想格上的GapSVP和SIVP 的复杂度分析并没有理论上的证明, 但是在最困难情况下,目前人们并没有找到环上相应格问题的多项式时间算法,因此有理由相信这些问题也是足够困难的(即使在量子算法下).
2 格密码体制的近期研究进展和主要思想
近2年以来,格密码体制的设计是密码学研究的热点问题之一.我们将分别从基于格的零知识证明、加密、签名和密钥交换4个方面来详细介绍这2年以来的研究进展,并简单阐述其涉及的主要思想和关键技术.
2.1基于格的零知识证明
零知识证明是证明者向验证者证明某个命题的真伪,但不泄露其他的任何信息.它可以用到密码学的很多领域,是格密码近期研究的热点问题.
基于格的零知识证明在加密、可验证加密和群签名等密码方案的应用方面,明文知识证明得到越来越多的关注.在明文知识的零知识证明体系中,一个拥有消息m的证明者生成一个密文t=Enc(m),然后它向验证证明它知道该消息m=Dec(t).也就是说,向验证者证明它知道Dec(t)的值,等价于证明密文t是由相应的消息m正确生成的.

1) 在格困难问题中采用Stern[18]的方法来构造,然而,利用该方法构造的方案效率较低.这是由于每轮协议有23的错误概率,因此要达到128比特的安全性,需要重复执行192次.
2) 另一个可行的思路是结合Rejection Sampling引理[19]利用Fait-Shamir技术[20].一般情况下,该方法下的协议每轮有12的错误概率,但由于该方法比Stern的有更多的代数结构,因此,近几年的主要进展都是基于该方法之上的.该方法的主要障碍是:当抽取一些短向量使得对于某个整数c,满足方程Ae′=tc时,即有Ae′c-1=t.不幸的是,除非c=±1,否则并不能保证e′c-1是一个短向量,这也正是基于格与基于离散对的Fait-Shamir技术的主要不同之处.需要注意的是,该障碍在理想格上仍旧存在.
在2014年亚洲密码年会上,Benhamouda等人[21]利用ring-LWE成功地将错误概率降到12n,其中n是ring-LWE的维数(例如取1 024).因此实际情况下,对于128 b的安全性,只需要执行12次协议.然而,有趣的是该思路的构造只适用于理想格的情况,其背后的主要技术是利用了一个重要的引理,该引理保证了环[X]〈Xn+1〉上的某些二项式是可逆的,并且它们的逆仅仅有很小的整系数.其具体叙述为:设n是2的次幂,且0 在2016年美密会上,Baum等人[22]提出了一个新的诚实验证者零知识证明协议.该协议的主要思想是构造了一个在整数向量上的同态单向函数f:r→G,其中G是一个阿贝尔群,运用的关键技术之一是在向证明者提取知识时,运用了cut-and-choose rewinding技术;其次作者高效地利用了Lyubashevsky[19]的Rejection Sampling引理,其主要思想是:证明者收到的挑战值c能够显示witness的部分信息时,可以选择终止协议. 在2017欧洲密码年会上,Lyubashebsky等人[16]利用明文知识证明构造了一个可验证加密方案.其背后的基本思路是:给定矩阵B∈p和线性关系式Bm=umodp,设法生成一个密文和一组“low-weight”证据,使得密文的解密结果是并且满足关系式 (1) 目前基于格的零知识证明发展较快,基于LWE或ring-LWE构造高效的,且最好没有异常终止的零知识证明将会是今后研究的重点内容. 2.2基于格的加密 近几年来,基于格的加密方案大致沿着2条线.首先是对NTRU加密系统的改造,Stehle和Steinfeld在2011年首次对NTRU进行了成功改进[23],将方案的语义安全规约到了ring-LWE问题的困难性假设.在PKC 2017会议上,Yu等人[24]讨论了在素分圆环[X]〈Xn-1+…+X+1〉(其中n是奇素数)上的NTRU加密方案,得到一个标准模型下IND-CPA安全方案,其安全性可规约到理想格上的最坏情况的困难问题.提出这种环的研究主要是因为它比2011年Stehle的环更容易控制而且能抵抗子域攻击[25],此外注意到素分圆环[X]〈Xn-1+…+X+1〉是NTRU环[X]〈Xn-1〉的一个子环,因此基于素分圆环构造加密方案更接近于原始的NTRU加密系统. 另外,格加密方案大多应用LWE和ring-LWE问题构建某些特殊加密方案如谓词加密(predicate encryption)[26]、基于属性加密(attribute based encryption, ABE)[27-28]和可验证加密[16]等.例如文献[26]讨论了基于LWE的谓词加密,然而方案的构造借助于全同态加密(fully homomorphic encryption, FHE)机制,在分层电路到所有电路中用到了自举(bootstrap)的方法,方案的效率比较低.对于现有方案的一些改进方向大多都是不改动方案本身,单独优化FHE效率从而提高谓词加密的效率.最后,2014年亚洲密码年会Benhamouda等人[17]提出的零知识证明能够改进基于ring-LWE的加密方案;2017年欧洲密码年会Lyubashebsky等人[16]利用明文知识证明构造了一个可验证加密方案等.总之,基于格构造各种特殊的加密方案是格加密的重要发展趋势,丰富了格密码的研究内容. 2.3基于格的数字签名 近2年格上数字签名的研究成果,基本是利用Fiat-Shamir变换[15]这种思路来构造高效安全的签名方案[29-30].这种思路的构造一般要经历如下过程:困难问题→抗碰撞Hash函数→一次签名→身份认证协议→数字签名.以格上ring-SIS为例,下面我们给出该思路的大致过程. 取环R=p[X]〈Xn+1〉,定义抗碰撞Hash函数ha(z)=a·z,其中a∈m,z∈Dm⊆m.首先我们就可以构造一个三轮的身份认证协议[15]: 1) 证明者在R中随机选取一个向量y,根据实际情况可以对它的范数适当限制; 2) 证明者向验证者发送b=h(y); 3) 验证者选取一个随机的“挑战”c,并发送给证明者; 4) 证明者的应答为r=y+zc; 5) 验证者验证h(r)=b+h(z)c. 注意到上述协议如果不加上承诺y,该应答将完全恢复私钥z,因此承诺y的作用主要是隐藏私钥.把协议中的验证者替换为随机预言机,利用Fiat-Shamir变换就可以构造出一个数字签名方案. 需要特别注意的是,通过该思路构造的签名输出y+zc要保证不能包含私钥的任何有用信息,这个问题在基于整数分解和离散对数的签名中很容易解决,但在基于格的数字签名中,由于格特殊的代数结构,这是格签名发展的主要障碍.一个比较直观的解决办法是:相对于zc,我们可以在足够大的范围内随机选取向量y,那么y+zc的值就会以很大的概率在y的范围随机分布,如果敌手对y一无所知,那么它就不会获取私钥z的任何信息.但是这种解决办法y的值很大,因此输出的签名y+zc的签名长度就会很长,所以在构造签名时,该方法很少被利用.除此之外,目前主要的有效的解决途径主要有2种方法: 1) aborting技术[15].它的主要思想是签名者可以有选择性的输出签名,以保证签名不包含私钥的任何有用信息.具体地讲,我们主要运用下面这个论断:如果我们要计算2个数的和,其中a∈[-A,A],b←[-3A,3A],那么,当且仅当c∈[-2A,2A]时,我们才输出c=a+b.否则,重新选择b,直至上述条件成立.在这种情形下,我们就能保证c的输出分布与a是无关的.利用这个思想,当有选择性的输出签名时,就可以保证签名的输出分布与私钥是无关的. 2) Rejection Sampling引理[16].为了便于理解,我们给出该引理的具体内容:设f:n→是一个概率分布.给定一个子集V⊆n,令h:V→定义在V上的概率分布,gv:n→是一个的概率分布族,使得几乎对于所有的v∈V,都存在一个上界M∈使得: Pr[Mgv(z)≥f(z);z←f]≥1-negl(λ), 则下面2个分布的统计距离可忽略不计: 也就是说,给定一个概率密度函数f,找另一个密度函数g,满足f(z)≤Mg(z).然后分别以函数f和g进行抽样并以一定概率输出,以保证f和g的输出分布的统计距离是可忽略的.在签名方案的构造过程中,实际上找函数g的过程就是构造签名的过程. 近几年来,格上数字签名主要以上述2种方法为基础来构造高效安全的签名方案.在CT-RSA 2014 上,Bai和Galbraith[29]在生成签名的过程中,先用rounding算子对承诺值v的比特取高位,也就是扔掉一些最不重要的比特位,然后再取它与签名消息μ的Hash值c,然后根据上述方法即可得到一个基于LWE的短签名方案.注意:为了保证承值v扔掉一部分值后仍能够验证成功,需要控制好方案中一些参数的取值. 在2016亚洲密码年会上,Lyubashevsky[30]利用Fiat-Shamir变换基于所有环q[X]〈f〉的ring-SIS问题构造了一个高效的签名方案,这里仅仅对f的次数进行了较弱的限制.它的主要贡献是:之前的文章在利用理想格构造数字签名时,往往用一些特殊的环,如NTRU环[X]〈Xn-1〉和素分圆环[X]〈Xn-1+…+X+1〉.目前为止,虽然还没有对这种环的worst-case困难问题实质有效的攻击,但是,文献[31]利用某些特殊环的代数结构,解决了这些环的一些其他困难问题,Cramer等人[31]在量子计算下构造了一个多项式时间算法,该算法能够解决分圆环中主理想的近似因子为最短向量问题.而文献[30]在很大程度上放宽了对f的限制,这里仅仅要求函数f的次数有一个合理的上界,这在一定程度上增加了方案的安全性. 总之,目前格签名的密钥和签名长度有了进一步的缩短.但是,构造高效的格签名的思路比较单一,如何丰富格签名的构造将会是一个有趣的方向.另外,相比较于传统的签名方案,格签名的签名长度还有待于缩短,这也是格签名进一步研究的方向. 2.4基于格的密钥交换 对于基于格的密钥交换协议的构造,近几年出现许多优秀成果,如文献[32-38].其思路基本是根据Diffie-Hellman密钥交换协议的思想,直接由LWE问题直接构造.其关键问题一般在于金正中和赵运磊[32]首次提出的密钥共识,也就是说,它能基于交换双方持有的近似值达成共识.除了文献[32]中的一般构造算法,一种思路是Ding等人[33]提出的robust extractor.更具体地说,robust extractor是这样的一个确定性算法E,它满足对于任意x,y∈q,如果x-y是偶数,且其绝对值足够小,那么E(x,σ)=E(y,σ),其中σ∈{0,1}. 另一个较为常用的思想是Peikert[34]在2014年提出的Reconciliation技术.由于后续的密钥交换协议基本都是建立在Peikert的Reconciliation技术基础之上,下面结合其密钥封装机制的基本构造(如图1所示),简述其基本思想. AliceBobKEM.Gen(a):s,e←χb=as+eKEM.Decaps(s,(u,v′)):μ=rec(2us,v′)b→u,v′← KEM.Encaps(a,b):s′,e′,e″←χu=as′+e′v=bs′+e″ v←dbl(v)v′=〈 v〉2μ=[ v]2 Fig. 1 Peikert’s key-encapsulation mechanism图1 Peikert密钥封装机制 向量a随机选取于环q,其中对于Alice,环元素是us=ass′+e′s,对于Bob,则为v=bs′+e″=ass′+es′+e″.在不泄露双方私钥的情况下,为了保证得到完全相同的分担密钥,Peikert定义〈v〉2对于随机选取的定义随机函数dbl(v)其中的概率为,分别取和的概率均为.令则调节函数定义为 在CCS 2016大会上,Bos等人[36]基于Peikert的调节机制给出了一个新的、较实用的密钥交换协议Frodo.与之前效率较好的协议相比,该方案的安全性基于困难性更好的LWE问题.协议的构造主要从2个方面进行改进:1)在不增加高斯抽样维数的前提下,作者给出了抽样效率更高的由离散概率密度函数构成的扰动分布;2)相比于Peikert的密钥封装机制,作者构造了一个更一般的调解机制,即对每个约定允许提取更多的分担比特.尽管它以增加了调解失败概率为代价,但是概率的增加足够小,并不会影响到实际的应用.正如文献[36]所述,为了使协议达到足够的安全程度,需要满足固定关系式m×n×B≥256,其中m,n是LWE问题的维数,B是上述允许提取的分担比特值.因此,当B比较大时,反过来可以降低LWE矩阵的维数.如此不仅能有效地减小带宽,而且能有效地避免某些预计算攻击,例如CCS 15会议[38]上提出的针对Diffie-Hellman交换协议的Logjam攻击,实际上这种攻击对格上的密钥交换协议的安全性更具有毁灭性[35]. 本文简单介绍了格困难问题的求解和计算复杂性的基本结论,并对近期格密码的发展状况进行简单总结.虽然格困难问题在密码体制的设计和安全性方面有着很大的潜力,但仍有许多问题还不明朗,有待于密码学家进一步去研究、验证.如关系到密码方案参数选取的LLL算法在具体实现中却比理论结果要好,这个问题目前也没有合理的解释.此外,理想格上的问题应该比普通格上的相应问题更加简单,虽然在最困难情况下,目前人们并没有找到环上相应格问题的多项式时间算法,但是理想格上的如GapSVP和SIVP问题的复杂度分析并没有理论上的证明.因此,这些都是密码学家进一步努力的方向. 在格密码体制的设计方面,格密码在安全性方面有着很大的潜力,但在效率和实用性方面,它与目前传统的较实用的密码方案还有很大的差距,格密码的研究历程还有很长的路要走.例如签名长度过大一直就是格签名实例化的一个主要障碍,密码学家为此做了很多努力,而基于理想格的签名方案就指明了一个可行性的方向. 总之,格密码已经成为当前密码学研究的热点,无论从理论还是实用价值方面,格密码都有很大的潜力,但是它仍需要进一步完善和发展. [1] Lenstra A K, Lenstra H W, Lovász L. Factoring polynomials with rational coefficients[J]. Mathematische Annalen, 1982, 261(4): 515-534 [2] Shamir A. A polynomial-time algorithm for breaking the basic Merkle-Hellman cryptosystem[J]. IEEE Trans on Information Theory, 1984, 30(5): 699-704 [3] Coppersmith D. Finding a small root of a univariate modular equation[G] //LNCS 1070: Proc of EUROCRYPT 96. Berlin: Springer, 1996: 155-165 [4] Ajtai M. Generating hard instances of lattice problems[G] //Proc of ACM Symp on Theory of Computing 1996. New York: ACM, 1996: 99-108 [5] Ajtai M, Dwork C. A public-key cryptosystem with worst-case/ average-case equivalence[G] //Proc of ACM Symp on Theory of Computing 1997. New York: ACM, 1997: 284-293 [6] Hoffstein J, Pipher J, Silverman J H. NTRU: A ring-based public key cryptosystem[G] //LNCS 1423: Proc of Int Algorithmic Number Theory Symp. Berlin: Springer, 1998: 267-288 [7] Gentry C. Fully homomorphic encryption using ideal lattices[C] //Proc of ACM Symp on Theory of Computing 2009. New York: ACM, 2009: 169-178 [8] Rivest R L, Adleman L, Dertouzos M L. On data banks and privacy homomorphisms[J]. Foundations of Secure Computation, 1978, 4(11): 169-180 [9] Wang Xiaoyun, Liu Mingjie. Survey of lattice-based cryptography[J]. Journal of Cryptologic Research, 2014, 1(1): 13-27 (in Chinese) (王小云, 刘明洁. 格密码学研究[J]. 密码学报, 2014, 1(1): 13-27) [10] Peikert C. A decade of lattice cryptography[J]. Foundations and Trends in Theoretical Computer Science, 2016, 10(4): 283-424 [11] Chen L, Jordan S, et al. Report on Post-Quantum Cryptography[M]. Gaithersburg: US Department of Commerce, National Institute of Standards and Technology, 2016 [12] Shor P W. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer[J]. SIAM Journal on Computing, 1997, 26(5): 1484-1509 [13] Schnorr C P. A hierarchy of polynomial time lattice basis reduction algorithms[J]. Theoretical Computer Science, 1987, 53(2/3): 201-224 [14] Schnorr C P, Euchner M. Lattice basis reduction: Improved practical algorithms and solving subset sum problems[J]. Mathematical Programming, 1994, 66(1/2/3): 181-199 [15] Chen Yuanmi, Nguyen P Q. Bkz 2.0: Better lattice security estimates[G] //LNCS 7073: Proc of ASIACRYPT 2011. Berlin: Springer, 2011: 1-20 [16] Lyubashevsky V, Neven G. One-shot verifiable encryption from lattices[G] //LNCS 10210: Proc of EUROCRYPT 2017. Berlin: Springer, 2017: 293-323 [17] Benhamouda F, Camenisch J, Krenn S, et al. Better zero-knowledge proofs for lattice encryption and their application to group signatures[G] //LNCS 8873: Proc of ASIACRYPT 2014. Berlin: Springer, 2014: 551-572 [18] Stern J. A new identification scheme based on syndrome decoding[G] //LNCS 773: Proc of CRYPTO 1993. Berlin: Springer, 1993: 13-21 [19] Lyubashevsky V. Lattice signatures without trapdoors[G] //LNCS 7237: Proc of EUROCRYPT 2012. Berlin; Spring, 2012: 738-755 [20] Lyubashevsky V. Fiat-shamir with aborts: Applications to lattice and factoring-based signatures[G] //LNCS 5912: Proc of ASIACRYPT 2009. Berlin: Springer, 2009: 598-616 [21] Benhamouda F, Camenisch J, Krenn S, et al. Better zero-knowledge proofs for lattice encryption and their application to group signatures[G] //LNCS 8873: Proc of ASIACRYPT 2014. Berlin: Springer, 2014: 551-572 [22] Baum C, Damgrd I, Larsen K G, et al. How to prove knowledge of small secrets[G] //LNCS 9816: Proc of CRYPTO 2016. Berlin: Springer, 2016: 478-498 [23] Stehlé D, Steinfeld R. Making NTRU as secure as worst-case problems over ideal lattices[G] //LNCS 6632: Proc of EUROCRYPT 2011. Berlin: Springer, 2011: 27-47 [24] Yu Yang, Xu Guangwu, Wang Xiaoyun. Provably secure NTRU instances over prime cyclotomic rings[G] //LNCS 10174: Public - Key Cryptography 2017. Berlin: Springer, 2017: 409-434 [25] Albrecht M, Bai S, Ducas L. A subfield lattice attack on overstretched NTRU assumptions[G] //LNCS 9814: Proc of CRYPTO 2016. Berlin: Springer, 2016: 153-178 [26] Gorbunov S, Vaikuntanathan V, Wee H. Predicate encryption for circuits from LWE[G] //LNCS 9216: Proc of CRYPTO 2015. Berlin: Springer, 2015: 503-523 [27] Gorbunov S, Vaikuntanathan V, Wee H. Attribute-based encryption for circuits[C] //Proc of ACM Symp on Theory of Computing 2013. New York: ACM, 2013: 545-554 [28] Boneh D, Gentry C, Gorbunov S, et al. Fully key-homomorphic encryption, arithmetic circuit ABE and compact garbled circuits[G] //LNCS 8841: Proc of EUROCRYPT 2014. Berlin: Springer, 2014: 533-556 [29] Bai S, Galbraith S D. An improved compression technique for signatures based on learning with errors[G] //LNCS 8366: Proc of Topics in Cryptology CT-RSA 2014. Berlin: Springer, 2014: 28-47 [30] Lyubashevsky V. Digital signatures based on the hardness of ideal lattice problems in all rings[G] //LNCS 10032: Proc of ASIACRYPT 2016. Berlin: Springer, 2016: 196-214 [31] Cramer R, Ducas R, Peikert C, et al. Recovering short generators of principal ideals in cyclotomic rings[G] //LNCS 9666: Proc of EUROCRYPT 2016. Berlin: Springer, 2016: 559-585 [32] Jin Zhenzhong, Zhao Yunlei. Optimal key consensus in presence of noise[J]. ArXiv Preprint.ArXiv:1611.06150, 2016 [2017-08-15]. http://arxiv.org/pdf/1611.06150.pdf [33] Ding Jintai, Xie Xiang, Lin Xiaodong. A simple provably secure key exchange scheme based on the learning with errors problem[J]. IACR Cryptology Eprint Archive, 2012 [2017-08-15]. http://ai2-s2-pdfs.s3.amazonaws.com/b1e7/faec59a9bdd70e75f9d15496cf27916ce060.pdf [34] Peikert C. Lattice cryptography for the Internet[G] //LNCS 8772: Post-Quantum Cryptography 2014. Berlin: Springer, 2014: 197-219 [35] Alkim E, Ducas L, Pöppelmann T, et al. Post-quantum key exchange—A new hope[C] //Proc of the 25th USENIX Security Symp. Berkeley, CA: USENIX Association, 2016: 327-343 [36] Bos J, Costello C, et al. Frodo: Take off the ring! practical, quantum secure key exchange from LWE[C] //Proc of Conf on Computer and Communications Security 2016. New York: ACM, 2016: 1006-1018 [37] Zhang Jiang, Zhang Zhenfeng, Ding Jintai, et al. Authenticated key exchange from ideal lattices[G] //LNCS 9057: Proc of EUROCRYPT 2015. Berlin: Springer, 2015: 719-751 [38] Adrian D, Bhargavan K, Durumeric Z. Imperfect forward secrecy: How Diffie-Hellman fails in practice[C] //Proc of Conf on Computer and Communications Security 2015. New York: ACM, 2015: 5-17ZhangPingyuan, born in 1988. PhD candidate. His main research interests include public key cryptography, especially lattice-based cryptography. RecentAdvancesinLattice-BasedCryptography Zhang Pingyuan1,2, Jiang Han1, Cai Jie1,2, Wang Chenguang1,2, Zheng Zhihua3, and Xu Qiuliang1 1(CollegeofSoftware,ShandongUniversity,Jinan250101)2(SchoolofMathematics,ShandongUniversity,Jinan250100)3(CollegeofInformationScienceandEngineering,ShandongNormalUniversity,Jinan250358) Lattice theory was first introduced to cryptography as a cryptanalysis tool to analyze knapsack and RSA cryptosystem. In 1997, Ajtai and Dwork constructed the first lattice cryptography: Ajtai-Dwork; and then in 1998, NTRU is appeared. Since factorization and discrete logarithm based cryptography was the mainstream, lattice-based cryptography has not enough attention. Until 2009, Gentry constructed the first fully homomorphic encryption, which led to a wide of development of lattice cryptography. In 2015, Peikert made a summary of the development of lattice cryptography in “A decade of lattice cryptography”. Also in 2015, NIST released “Report on post-quantum cryptography”. According to the report, due to the rapid development of quantum computation technology, the existing standard of public key cryptography in quantum computing will be no longer safe. At the same time, NIST has launched a worldwide collection of quantum cryptography algorithms. As a classic quantum-resistant cryptography, lattice-based cryptography is known as the most promising competitor. Therefore, lattice cryptography has attracted much attention in recent years, and a lot of excellent results have been appeared. In this paper, we summarize the main results of lattice cryptography for the past two years, which consist of zero-knowledge proofs, encryption, signature and key exchange; and at last, we outlook the development trend of lattice-based cryptography. lattice-based cryptography; lattice-based zero-knowledge proof; lattice-based encryption; lattice-based signature; lattice-based key exchange TP309 JiangHan, born in 1974. Lecturer of Shandong University since 2009. His main research interests include cryptography and infor-mation security, especially secure multi-party computation. CaiJie, born in 1986. PHD candidate in Shandong University. Her main research interests include cryptography, especially lattice-based cryptographic protocols. WangChenguang, born in 1982. PhD candidate in Shandong University and lecturer in Jining University. His main research interests include cryptography, complex analysis and mathematical modeling. ZhengZhihua, born in 1962. Associate professor in Shandong Normal University. Her main research interests include cryptographic algorithms and protocols. XuQiuliang, born in 1960. Professor and PhD supervisor in Shandong University. His main interests include public key cryptography and multi-party secure computation.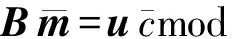
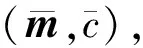
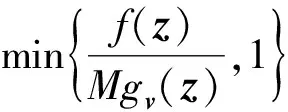
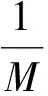


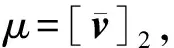
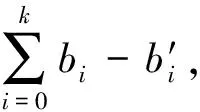
3 结束语







