一个双曲-椭圆耦合系统解的存在唯一性
师建国,周厚勇
(黄淮学院数学与统计学院,河南驻马店 463000)
一个双曲-椭圆耦合系统解的存在唯一性
师建国,周厚勇
(黄淮学院数学与统计学院,河南驻马店 463000)
本文研究了一个双曲-椭圆耦合系统.通过能量方法建立了有关微分算子的一些先验估计,构造了一个闭线性算子,证明了该闭线性算子为一个有界收缩线性算子半群的无穷小生成元.在此基础上,利用半群理论具体证明了双曲-椭圆耦合系统解的存在唯一性.
双曲-椭圆耦合系统;解;存在唯一性;闭算子;半群理论
1 引言
Navier-Stokes方程组反映了粘性流体流动的基本力学规律,它是流体力学、气象学、航天学、环境工程和数学中非常重要的方程组之一,可以用于水流、空气动力学的研究以及污染效应的分析[1].它是个非线性偏微分方程组,对于像这样的非线性偏微分方程组求精确解非常困难和复杂,目前只有在某些十分简单的问题上能求得精确解,在大部分情况下,只能求得近似解[2–4].对于夹在上下两壁面之间且上下两壁面可渗透的流体流动,其满足Navier-Stokes方程组系统

对于像空气、水等流体的流动来说,Navier-Stokes方程组中流体的粘性系数ε往往是很小的,因此为了求得近似解,可利用奇异摄动理论使方程组简化[5–7]进而得到一致有效的近似解,也就是说可以研究上述Navier-Stokes方程组系统当ε→0时的极限问题.作为研究Navier-Stokes方程组系统极限问题的一部分,考虑它的简单一点儿的情况,研究线性化Navier-Stokes方程组系统当ε→0时的极限问题.考虑将Navier-Stokes方程组关于稳态解(0,0,−U)摄动后去掉非线性项的情况,即先令然后去掉非线性项即得
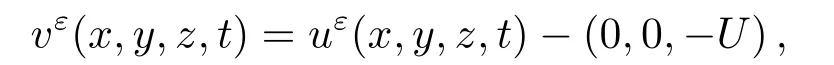
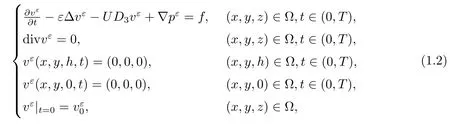
其中D3vε表示vε关于z的偏导数,这是一个线性化Navier-Stokes方程组系统.
注意(0,0,−U)是Navier-Stokes方程组当外力为零时的稳态解.
在研究线性化Navier-Stokes方程组系统极限问题时,利用奇异摄动理论结合解的适定性需要,得到了一个双曲-椭圆耦合系统
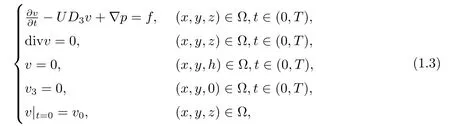
其中v=(v1,v2,v3)为无粘性流体的流速,p为压力,v,p在x方向以L1为周期,v,p在y方向以L2为周期,U为常数,Ω=(0,L1)×(0,L2)×(0,h).为了更好地研究线性化Navier-Stokes方程的极限问题,首先必须解决上述双曲-椭圆耦合系统解的存在唯一性问题.对于双曲-椭圆耦合系统,文献[8–10]研究了双曲-椭圆耦合系统的柯西问题,文献[11]研究了双曲-椭圆耦合系统的初边值问题,但边界条件和这里的边界条件差别较大.对于这里的初边值问题除文[7]给出了证明的大概思路外,目前还没有严格的证明结果.本文利用半群理论,通过能量方法具体证明了上述双曲-椭圆耦合系统中解的存在性唯一性.
2 一个闭线性算子的构造
为了给出弱解的定义,需要确定试验函数所在的空间以及解函数所在的空间.根据研究问题的边界条件特点和弱解对试验函数的要求取希尔伯特空间
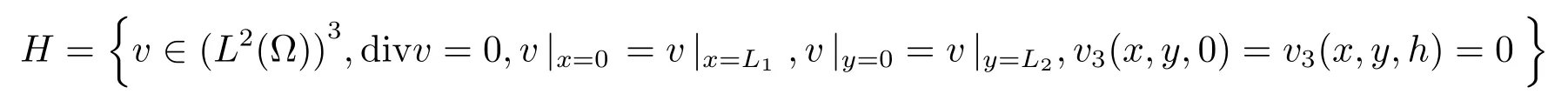
作为试验函数所在的空间.在研究线性化Navier-Stokes方程组的极限问题时,对弱解正则性是有一定要求的,比如要求D3v∈(L2(Ω))3或zD3v∈(L2(Ω))3,如果所研究的问题中没有压力项和divv=0,则在通常边界条件下,通过能量方法等,可以得到D3v的(L2(Ω))3模估计,根据解函数所在的空间对可解性和极限问题解的正则性的要求,可取
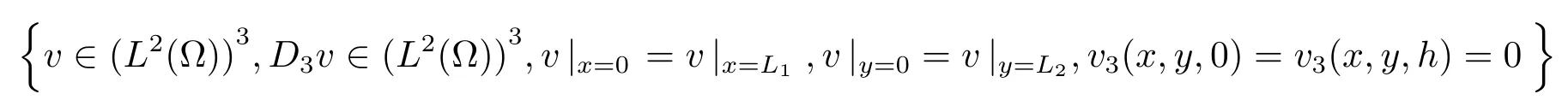
作为解函数所在的空间.但目前所研究的问题中含有压力项和divv=0,由所研究问题根据问题边界条件无法得到D3v的(L2(Ω))3模估计,但能得到zD3v的(L2(Ω))3模估计,这种估计也符合在研究线性化Navier-Stokes方程组极限问题时对弱解正则性的要求,因此根据解函数所在的空间对可解性和对弱解正则性的要求,这里确定
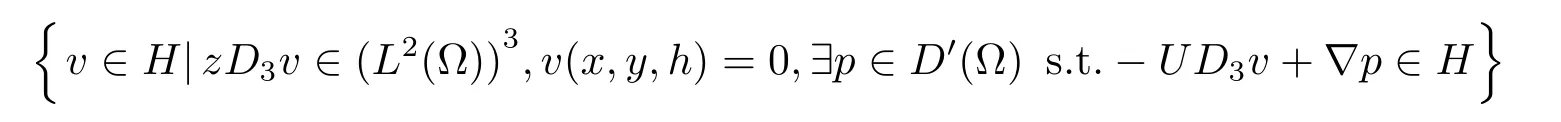
作为解函数所在的空间.为了以后使用方便,记
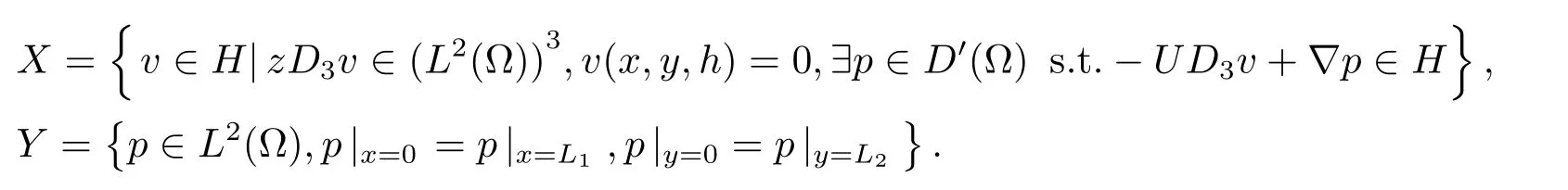
对X赋予以下范数:对任意对H和Y分别赋予(L2(Ω))3和L2(Ω)空间的范数.
为了研究问题(1.3)的解,对λ为实常数,首先给出问题
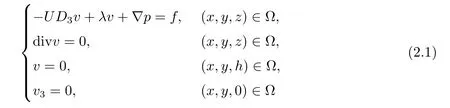
的弱解定义,进而构造闭线性算子.
定义若对v∈X,p∈Y有
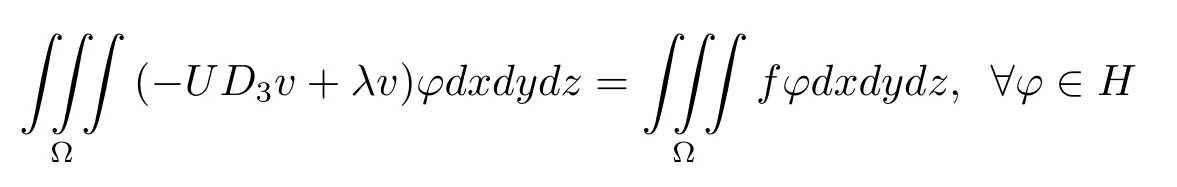
成立,则称(v,p)为问题(2.1)的弱解.
定理1对任意f∈H,对任意λ,问题(2.1)有唯一弱解v∈X,p∈Y,当λ>0时,有其中M1是只与区域Ω和λ>0有关的常数.
注这里要求f∈H是不失一般性的.事实上Hodge分解定理[12]告诉我们,对任意有唯一的正交分解u=w+▽q,divw=0且
对于一般的外力项f,由Hodge分解定理知f=f1+▽f2,divf1=0,则由
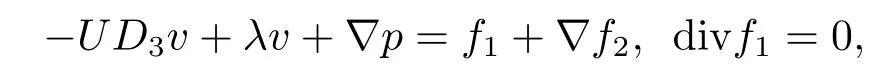
得
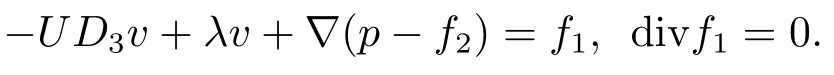
用p−f2,f1代替p,f即可.
证以z为参数做v∈X和p∈Y关于变量x,y的傅里叶变换容易证明对任意f∈H,对任意λ,问题(2.1)有唯一弱解v∈X,p∈Y.下面证明当λ>0时,有
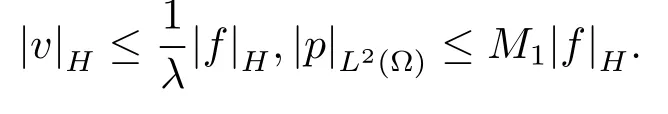
在方程−UD3v+λv+▽p=f两边分别与v∈X作内积,然后在Ω上积分并分部积分,注意到解的边界条件和不可压缩条件,有
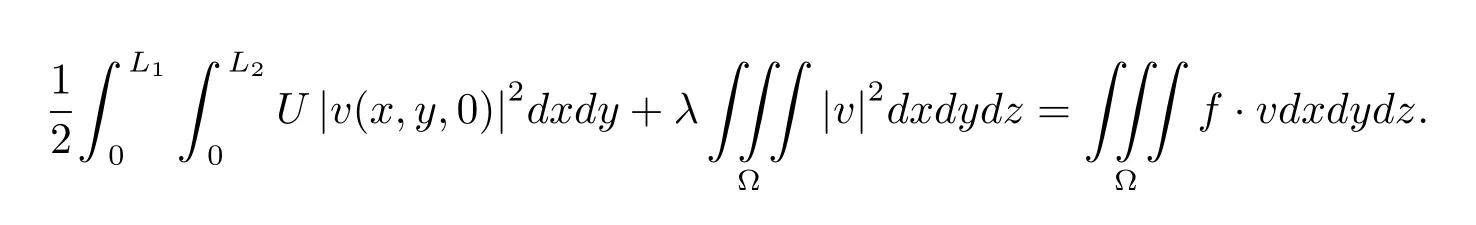
由上式并利用Holder不等式和Cauchy不等式得
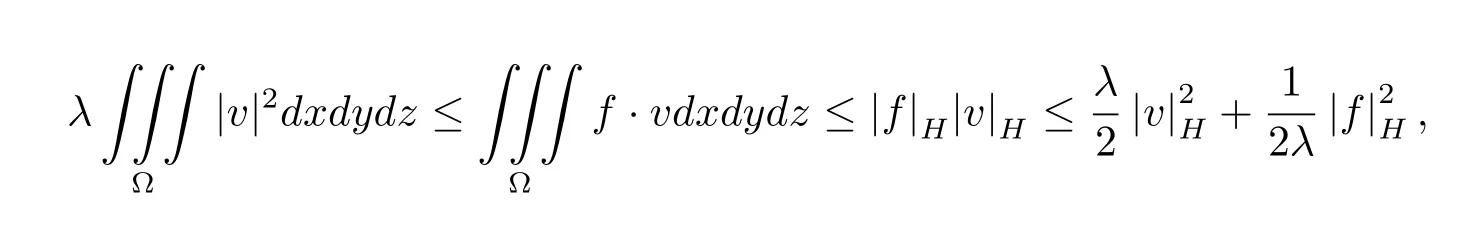
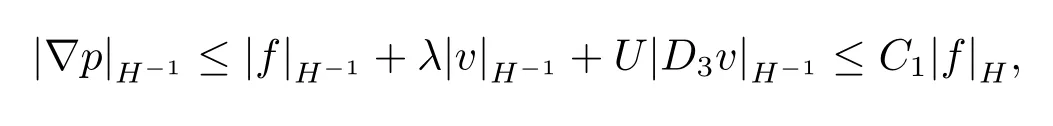
其中C1是只与区域Ω和λ>0有关的常数.
由Magenes-Stampacchia的结果[13]得|p|L2(Ω)≤M1|f|H,证毕.
由定理1,对任意f∈H,对任意λ,问题(2.1)有唯一弱解v∈X,p∈Y,为此可以利用问题(2.1)的解v∈X,f∈H,定义线性算子Aλ如下:Aλv=f,Aλ的定义域D(Aλ)=X.
由定理1,对任意f∈H,λ=0,有v∈X,p∈Y是问题
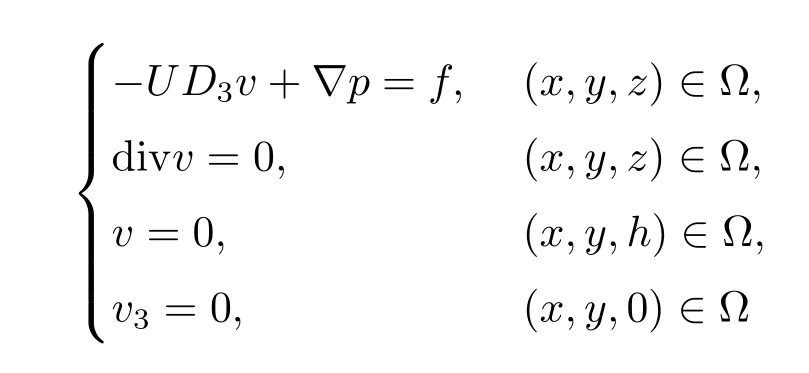
的弱解.对此定义算子A:Av=f,D(A)=X,显然A=Aλ−λI或Aλ=A+λI.
定理2对问题(2.1)的任意弱解v∈X,当λ>0时,有‖v‖X≤M2|f|H,其中M2是只与区域Ω和λ有关的常数.
证在方程−UD3v+λv+▽p=f两边分别与−z2D3v∈(L2(Ω))3作内积,然后在Ω上积分并分部积分,注意到解的边界条件和不可压缩条件,利用Holder不等式和Cauchy不等式得
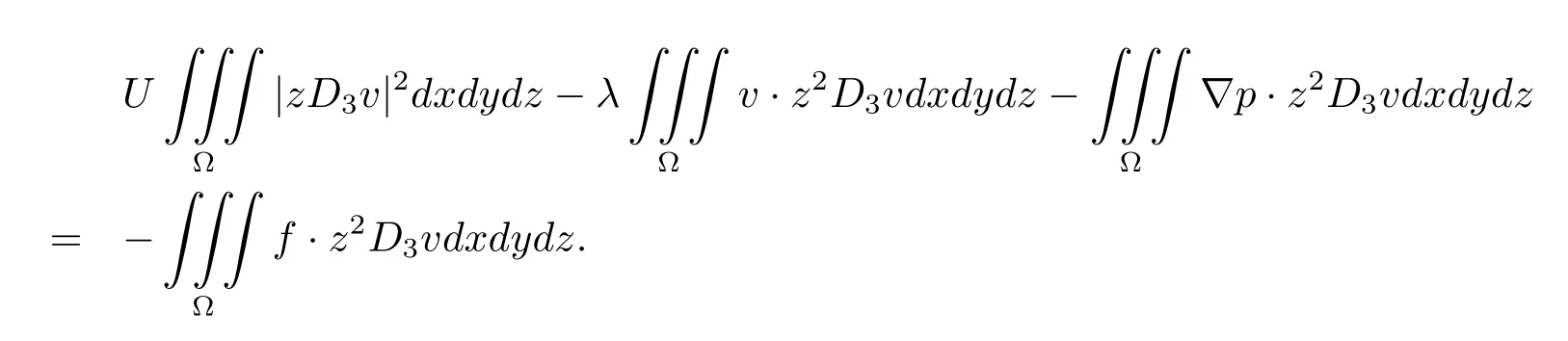
注意到v(x,y,h,t)=0,有
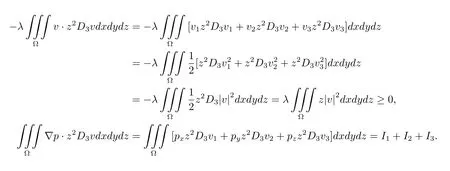
注意到v,p在x方向以L1为周期,v,p在y方向以L2为周期,得
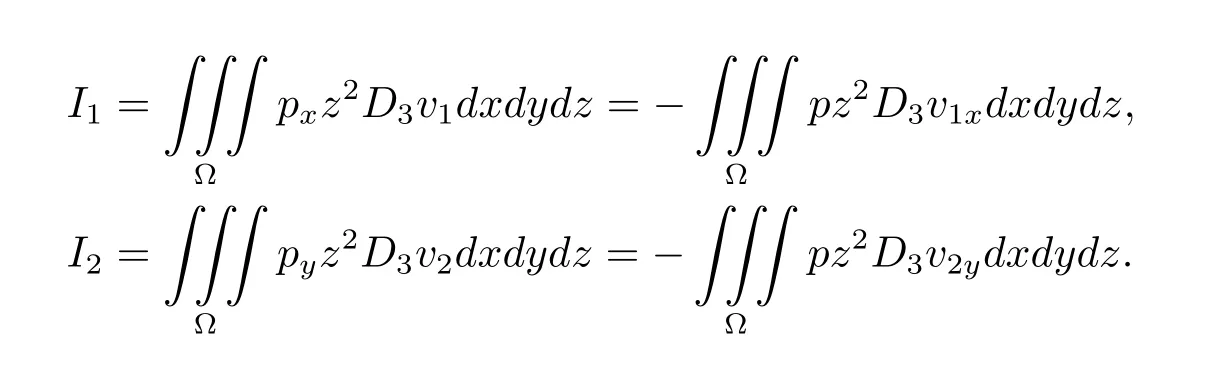
因为v1(x,y,h)=v2(x,y,h)=0,所以v1x(x,y,h)=v2y(x,y,h)=0,又由不可压条件知v1x(x,y,h)+v2y(x,y,h)+v3z(x,y,h)=0,进而v3z(x,y,h)=0,故

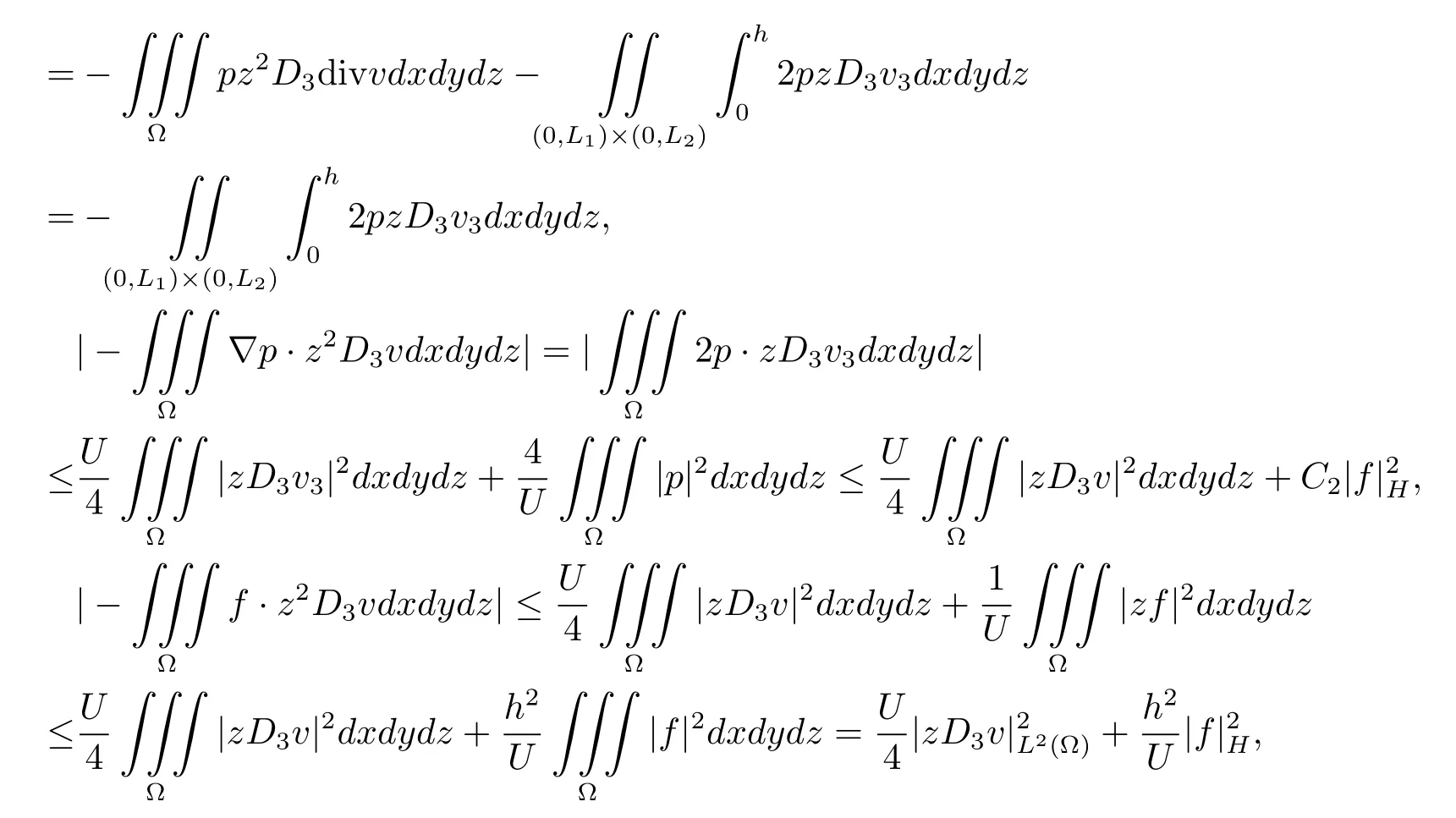
所以|zD3v|L2(Ω)≤C3|f|H,其中C2,C3是只与区域Ω和U,λ>0有关的常数.
注意到|UD3v−▽p|H=|f−λv|H,有‖v‖X≤M2|f|H.
定理3线性算子Aλ(λ>0)是一个闭线性算子.
证设vn∈D(Aλ),且在H中有vn→v,Aλvn=fn→f∈H,由Aλ定义知vn∈X,pn∈Y是问题(2.1)的解,进而满足
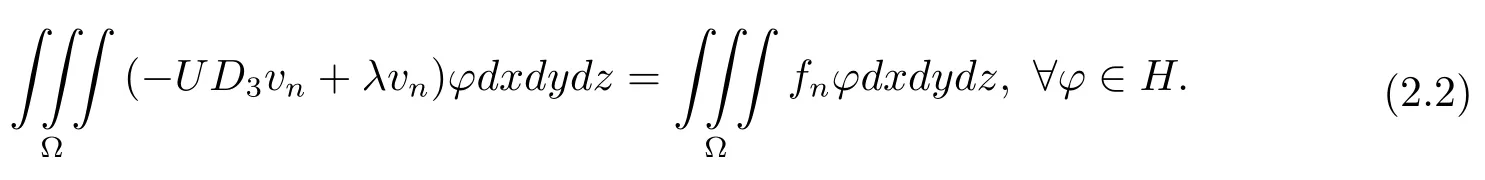
对于f∈H,由定理1知,存在使得是问题(2.1)的解,从而是问题(2.1)的解,则由定理2有所以vn在X收敛于又X是H的子空间,所以即vn在X收敛于v,在(2.2)式和中令n→∞得
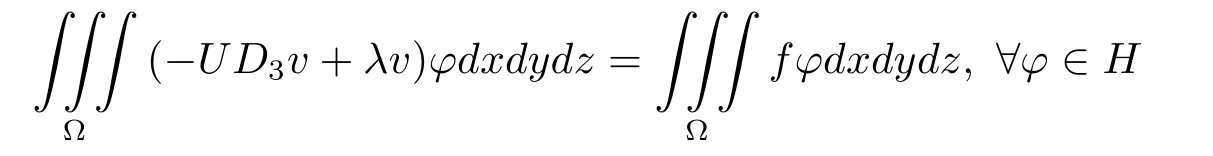
且‖v‖X≤M2|f|H,即v∈D(Aλ)=X,Aλv=f,所以线性算子Aλ是闭线性算子.
注容易证明若B是D(B)到H中的闭线性算子,则B+ωI是D(B)到H中的闭线性算子,其中ω为一个常数.
利用定理3和上面的事实,注意到A=Aλ−λI,有
定理4线性算子A是一个D(A)=X到H中的闭线性算子.
3 双曲-椭圆耦合系统解的存在唯一性
定理5设f∈C1([0,+∞);H),v0∈H,则双曲-椭圆耦合系统(1.3)在C1(R+;D(A))∩C1(R+;H)中存在唯一解.
证由定理4知线性算子A是一个D(A)=X到H中的闭线性算子,从而−A也是闭线性算子.
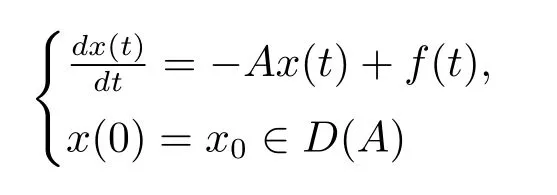
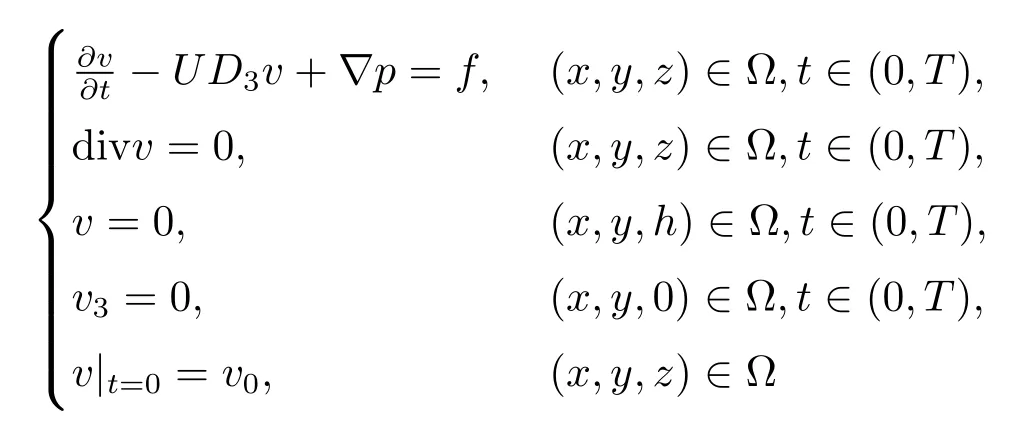
在C1(R+;D(A))∩C1(R+;H)中存在唯一解.
[1]王言英.格林函数与纳维–斯托克斯方程及其在船舶与海洋工程中的应用[M].北京:国防工业出版社,2006.
[2]Feng Yihu,MO Jiaqi.Asymptopic solution for singularly perturbed fractional order differential equation[J].J.Math.,2016,36(2):239–245.
[3]水庆象,王大国.N-S方程基于投影法的特征线算子分裂有限元求解[J].力学学报,2014,46(3):369–380.
[4]Wang D G,Wang H J,Xiong J H,Tham L G.Characteristic-based operator-splitting finite element method for Navier-Stokes equations[J].Sci.China(Tech.Sci.),2011,54(8):2157–2166.
[5]Foias C,Manley O,Rosa R,Temam R.Navier-Stokes equations and turbulence encyclopedia of mathematics and its applications[M].Cambridge:Cambridge University Press,2001.
[6]Weinan E.Boundary layer theory and the zero viscosity limit of the Navier-Stokes equation[J].Acta Math.Sin.(English Ser.),2000,16(2):207–218.
[7]Temam R,Wang X.Boundary layers associated with incompressible Navier-Stokes equations:the noncharacteristic boundary case[J].J.Di ff.Equ.,2002,179(2):647–686.
[8]Kawashima S,Nishibata S.A singular limit for hyperbolic-elliptic coupled systems in radiation hydrodynamics[J].Indiana Univ.Math.J.,2001,50(1):567–589
[9]Ruan L Z,Zhang J.Asymptotic stability of rarefaction wave for hyperbolic-elliptic coupled system in radiating gas[J].Acta Math.Sci.,2007,27(2):347–360
[10]Gao W L,Zhu C J.Asymptotic decay toward the planar rarefaction waves for a model system in radiating gas in two dimensions[J].Math.Models Meth.Appl.Sci.,2008,18(4):511–541.
[11]Ruan L Z,Zhu C J.Asymptotic decay toward rarefaction wave for a hyperbolic-elliptic coupled system on half space[J].J.Part.Di ff.Eqs.,2008,21(2):173–192.
[12]马天.从数学观点看物理世界:几何分析引力场与相对论[M].北京:科学出版社,2012.10
[13]Magenes E,Stampacchia G.I problemi al contorno per le equazioni differenziali ditipo ellittico[J].Ann.Scuola.Norm.Sup.Pisa.,1958,12(3):247–357.
[14]张恭庆,林源渠.泛函分析讲义[M].北京:北京大学出版,2008.
THE EXISTENCE AND UNIQUENESS OF THE SOLUTIONS TO THE HYPERBOLIC-ELLIPTIC COUPLED SYSTEM
SHI Jian-guo,ZHOU Hou-yong
(School of Mathematics and Statistics,Huanghuai College,Zhumadian 463000,China)
In this paper,we study the hyperbolic-elliptic coupled system. By the energy method,we establish a priori estimates of the differential operator,construct the closed linear operator and claim the closed linear operator is the in finitesimal generator of the bounded incompressible linear operator semigroup.We prove the existence and uniqueness of the solutions to the hyperbolic-elliptic coupled system by the semigroup theory.
the hyperbolic-elliptic coupled system;the solutions;the existence and uniqueness;the closed operator;semigroup theory
35M10
O175.28
A
0255-7797(2017)06-1253-08
2016-10-17接收日期:2017-01-24
河南省科技计划项目(基础与前沿)基金资助(162300410084).
师建国(1965–),男,河南遂平,教授,主要研究方向:偏微分方程.

