NEW PARTIAL DIFFERENCE SETS AND CYCLOTOMIC NUMBER PROPERTIES
ZHANG Yuan,PENG Mao
(School of Mathematics and Statistics,Nanjing University of Information Science and Technology,Nanjing 210044,China)
NEW PARTIAL DIFFERENCE SETS AND CYCLOTOMIC NUMBER PROPERTIES
ZHANG Yuan,PENG Mao
(School of Mathematics and Statistics,Nanjing University of Information Science and Technology,Nanjing 210044,China)
In this paper,the connections among the theory of cyclotomy,partial difference sets and strongly regular graphs are studied.By means of cyclotomy,a new family of partial difference sets are constructed and new properties of cyclotomic numbers are obtained in reverse.
partial difference set;cyclotomic number;strongly regular graph
1 Introduction
The word cyclotomy(German,“Kreistheilung”)means“circle-division”and refers to the problem of dividing the circumference of the unit circle into a given number,n,of arcs of equal lengths.By the theory of cyclotomy,we shall mean the special attack upon this problem discovered by Gauss in connection with the ruler-and-compass construction of the regular polygon ofnsides.
Letq=ef+1 be an odd prime power,and letθbe a fixed primitive element of GF∗(q).De finewhere(θe)denotes the multiplicative subgroup generated byθe.The cosetsare called the index classes or cyclotomic classes of orderewith respect to GF(q).
For fixediandj,we de fineto be the number of solutions of the equation

where 1=x0is the multiplicative unit of GF∗(q).That is,(i,j)is the number of ordered pairs such that
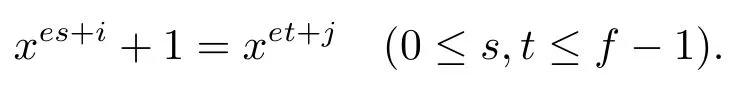
These constants(i,j)(e)qare called cyclotomic numbers of orderewith respect to GF(q),(i,j)in short if without any confusion.For more information about cyclotomic theory,one may be referred to[1]and[2–4].
It is easy to check the elementary relationships between the cyclotomic numbers.
(1)For any integersm,n,(i+me,j+ne)=(i,j).
(2)(i,j)=(e−i,j−i).
In 1953,Lehmer[5]established a simple and powerful connection between the theory of cyclotomy and the existence of difference sets.Since then,more and more difference sets were established by means of cyclotomic method.And also,some new properties of cyclotomy were achieved from the existence of difference sets.
De finition 1.1A partial difference setDis a subset of a groupGwith the property that every nonidentity element ofDcan be representedλtimes as a difference between a pair of elements inDwhile every nonidentity element ofGDcan be representedµtimes as a difference between a pair of elements inD.Likewise,partial difference sets have parameters(v,k,λ,µ)associated with them,wherev=|G|,k=|D|,andλandµare as described above.
In 1963,Bose[6]introduced the concept of strongly regular graphs.
De finition 1.2An undirected graph without loops and multiple edges onvvertices is called a(v,k,λ,µ)-strongly regular graph if it is regular with valencyk,and each adjacent pair of vertices hasλvertices,which are adjacent to both of them,also each non-adjacent pair of vertices hasµvertices,which are adjacent to both of them.
Clearly a disconnected strongly regular graph is a disjoint union of complete graphs of equal size.The complement of a strongly regular graph with parameters(v,k,λ,µ)is also a strongly regular graph with parameters(v,v−k−1,v−2k+µ−2,v−2k+λ).In consequence,we have the trivial necessary conditionv−2k+µ−2≥0 for the existence of a strongly regular graph.A simple counting argument shows that we also have the necessary conditionk(k−1)=kλ+(v−k−1)µ.For more information,one can be refered to[7–9].
As it is known that partial difference sets can be used to construct strongly regular graphs.
SupposeDis a(v,k,λ,µ)partial difference set inG.Let the elements ofGbe vertices of a graph,and join two verticesv1,v2with an edge ifv1−v2∈D.For all verticesv,they will havekedges going into them because each will be connected tov+dfor alld∈D.If we consider two verticesv1,v2,connected to a vertexx,thenx−v1∈Dandx−v2∈D.By taking(x−v1)−(x−v2)=v1−v2,this shows that there must beλvalues forxifv1−v2∈Dandµvalues forxifv1−v2∈GD.Thus if there is a partial difference set,there exist a strongly regular graph with the same parameters.So in this paper,we equate the two concepts if without confusion.
In this paper,we firstly give a construction of a family of partial difference sets which also means the existence of strongly regular graphs with the same parameters.Then we get new properties of cyclotomic numbers.
2 Construction of Partial Di ff erence Sets and Strongly Regular Graphs
Denoteq=ef+1,letD={(a,b):a,b∈Diat the same time,iruns from 0 toe−1},so we have|G|=q2,We will discuss the setDin groupGaccording to the value ofe.
2.1 e=2,3,4,6
In this subsection,q=2f+1,
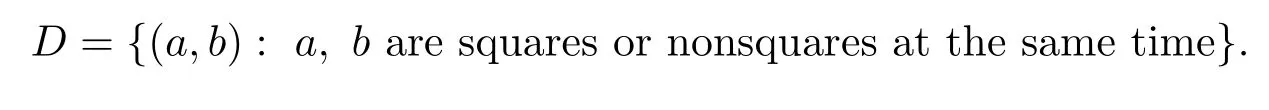
Whene=2,by the properties,the cyclotomic numbers are given as follows.Ifq≡1(mod 4),then
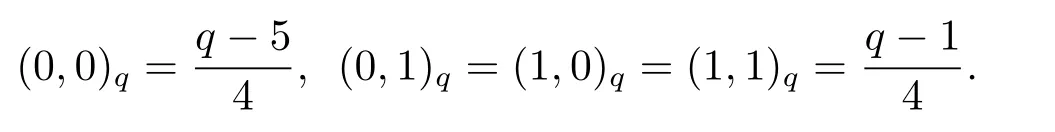
Ifq≡3(mod 4),then

We can compute the differences directly from the cyclotomic numbers,no matterfis odd or even.
·(a,0)appears as a difference,wherea≠0.That is,(a,0)=(a1,b1)−(a2,b1).

Table 1
·(0,b),whereb≠0,is the same as the above case,that is,(0,b)appearsf(f−1)times.
·(a,b)∈Dappears as a difference,that is(a,b)=(a1,b1)−(a2,b2),(ai,bi)∈D,i=1,2.

Table 2
We can see from the table that(a,b)∈Dappears as many times as the sum of the squares of all the cyclotomic numbers.
·(a,b)/∈Danda≠0,b≠0.(a,b)=(a1,b1)−(a2,b2).

Table 3
Hence,above all,
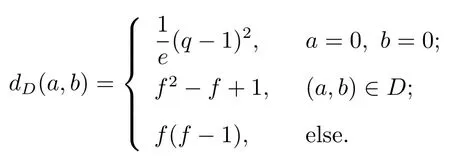
Obviously,Dis a partial difference set with parameters
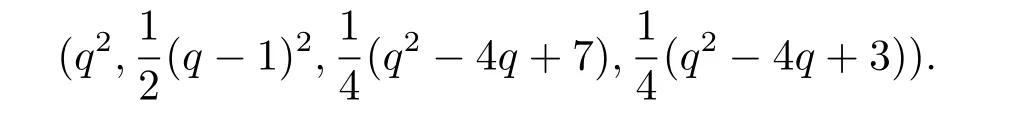
Example 1Whene=2,f=1,q=3=2×1+1.In GF(q),D0={1},D1={2},so
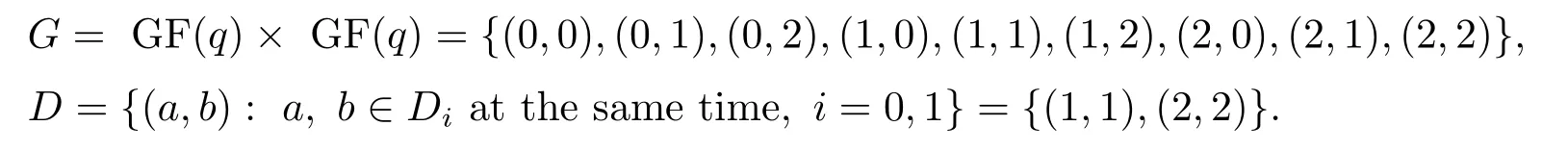
Obviously,Dis a(9,2,1,0)partial difference set.The corresponding strongly regular graph is Figure 1,which is disconnected.

Figure 1:(9,2,1,0)strongly regular graph
Example 2Whenf=2,q=5=2×2+1.In GF(q),D0={1,4},D1={2,3},so

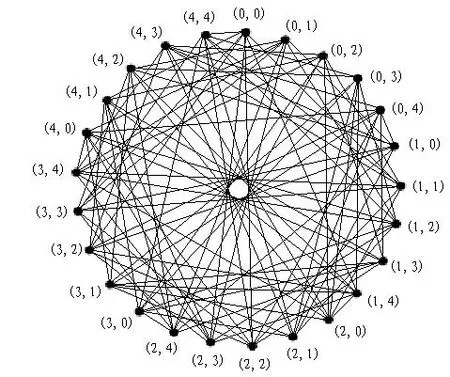
Figure 2:(25,8,3,2)strongly regular graph
Whene=3,4,6,following the same process,we have proved that whenq=ef+1 is a prime power,there existpartial difference sets,and also exist strongly regular graphs with the same parameters.Enlightened by the so trim form,we conjecture that the above result may also be true for other“e”s.
2.2 For General e
Theorem 2.1LetwhereDi×Distands for{(x,y)|x,y∈Di}.ThenDis a partial difference set in(GF(q)⊕GF(q),+).
We will prove the theorem by using character theory and a property of Gauss periods.
Let GF(q)be the finite field of orderq,whereq=pt,pis a prime.Letq=ef+1,wheree>1,and letgbe a primitive element ofGF(q).We use the following standard notationψ1:GF(q)→C is the additive character ofGF(q)such thatψ1(x)=ξTr(x)p,whereξpis a complex primitivepth root of unity and Tr is the absolute trace from GF(q).

are the Gauss periods.
The following well-known character theoretic characterizations of abelian partial difference sets will be used in our proof.
Lemma 2.2LetGbe an abelian group of ordervandDbe a subset ofGwith{d−1:d∈D}=D.ThenDis a(v,k,λ,µ)partial difference set inGif and only if,for any characterχofG,
据访问,南京普通高校定向运动开展的场地一般可分为两种,即校内场地与校外场地。校内场地的使用一般是整个校园,校外场地是南京的各个开放式公园。这些高校更多的会使用校内场地,较少使用校外场地。
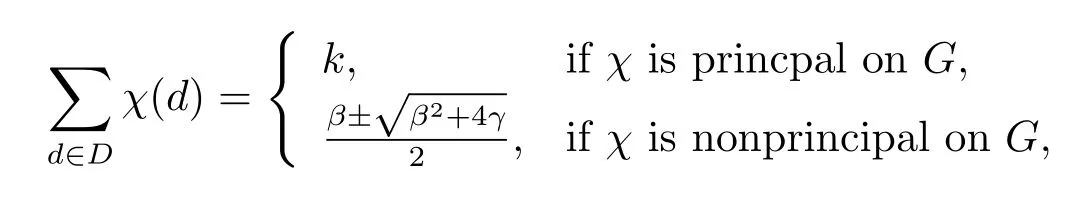
whereβ=λ−µ;γ=k−λife∈D,andγ=k−µif.
Proof of Theorem 2.1.Letψa⊗ψbbe a character of(GF(q)⊕GF(q),+).Then
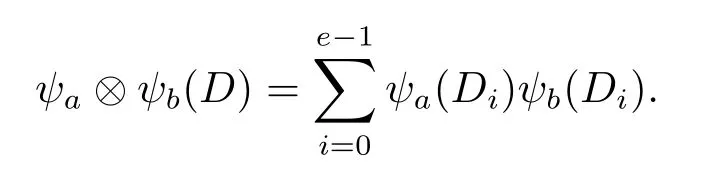
Ifa=0 orb=0(but not both),then one easily sees thatψa⊗ψb(D)=−f.
Ifa≠0 andb≠0,then
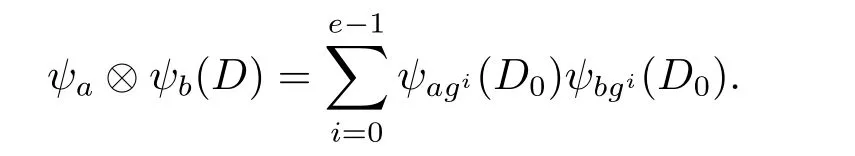
Letab−1=gl.Thenψa⊗ ψb(D)=Now note the following property of Gauss periodswhereδl,0=1 ifl=0 and it equals 0 otherwise.We have

Therefore we have shown that the character sumψa⊗ψb(D)takes two valuesq−f,−fasψa⊗ψbruns through all nontrivial characters of(GF(q)⊕GF(q),+).This proves thatDis a partial difference set.
It is not difficult to check the parameters are,f2+(e−3)f+1,f(f−1)).
From the point of the strongly regular graphs,supposeq=ef+1 is a prime power.Construct a graphGwithq2vertices.Label these vertices with(a,b),here(a,b)∈GF(q)×GF(q).LetD={Di×Di:i=0,1,···,e−1}.Call(a,b)~(a′,b′)i ff(a−a′(modq),b−b′(modq))∈D,we usually omit the“(modq)”if with none confusion.Since for any vertex(a,b),(a,b)~(a,b)+D,so the degree of(a,b)is|D|=(q−1)2.By Theorem 2.1,Gis a(q2,,f2+(e−3)f+1,f(f−1))strongly regular graph.
3 The New Properties of Cyclotomic Numbers
Since we have proved the existence of the partial difference sets,we can use it to get some properties of cyclotomic numbers in return.
As it is known that for a(v,k,λ,µ)partial difference setD,every nonidentity element ofDcan be representedλtimes as a difference between a pair of elements inDwhile every nonidentity element ofGDcan be representedµtimes as a difference between a pair of elements inD.
On the other hand,for any element(a,b),it can be represented as(a1,b1)−(a2,b2),here(a1,b1),(a2,b2)∈D.
(1)(a,b)∈D.

(2)(a,b)/∈D.
▪a=0 orb=0,but not both.
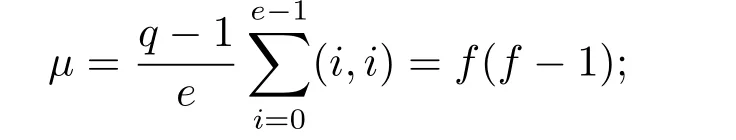
▪a≠0 andb≠0.Suppose(a,b)∈Di×Dj,0≤i,j≤e−1,i≠j,
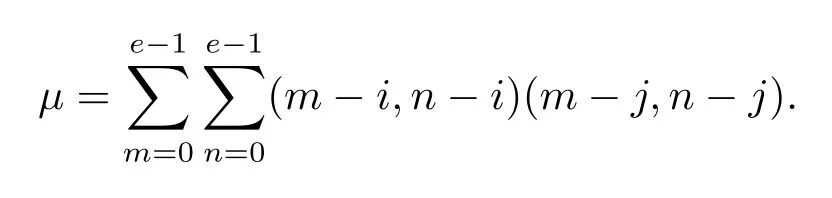
So we get the new properties of cyclotomic numbers.
Theorem 3.1Supposeq=ef+1 is a prime power.The cyclotomic numbers satisfy
[1]Storer T.Cyclotomy and difference sets[M].Chicago:Markhan,1967.
[2]Arasu K T,Ding C,Helleseth T,Kumar P V.Almost difference sets and their sequences with optimal autocorrelation[J].IEEE Trans.Inform.Theory,2001,47:2834–2843.
[3]Ding C,Helleseth T,Lam K Y.Several classes of binary sequences with three-level autocorrelation[J].IEEE Trans.Inform.Theory,1999,45:2606–2612.
[4]Ding C,Helleseth T,Martinsen H.New families of binary sequences with optimal three-level autocorrelation[J].IEEE Trans.Inform.Theory,2001,47:428–433.
[5]Lehmer E.On residue differences sets[J].Canad.J.Math.,1953,5:425-432.
[6]Bose R C.Strongly regular graphs,partial geometries and partially balanced designs[J].Pacific J.Math.,1963,13:389–419.
[7]Brouwer A E. Strongly regular graphs,the CRC handbook of combinatorial designs[M].C.J.Colbourn and J.H.Dinitz(Editors):CRC Press,1996:667–685.
[8]Brouwer A E,Cohen A M,Neumaier A.Distance regular graphs[M].Berlin,Heidelberg:Springer,1989.
[9]Calderbank R,Kantor W M.The geometryof two weight codes[J].Bull.London Math.Soc.,1986,18:97–122.
[10]Beth T,Jungnickel D,Lenz H.Design theory(2nd ed.)[M].Cambridge,UK:Cambridge University Press,1999.
[11]Bose R C,Dowling T A.A generalization of Moore graphs of diameter two[J].J.Combin.Theory Ser.B,1971,11:213–226.
[12]Brouwer A E.Some new two-weight codes and strongly regular graphs[J].Disc.Appl.Math.,1985,10:111–114.
[13]Bruck R H,Bose R C.Linear representations of projective planes in projective spaces[J].J.Alg.,1966,1:117–172.
[14]Feng Tao,Xiang Qing.Cyclotomic constructions of skew Hadamard difference sets[J].J.Comb.Theory,Ser.A,2012,119:245–256.
[15]Hamilton N,Quinn C.m-systems of polar spaces and maximal arcs in projective planes[J].Bull.Belg.Math.Soc.Simon Stevin,2000,7:237–248.
[16]Hirschfeld J W P.Projective geometries over finite fields[M].Oxford:Oxford University Press,1998.
[17]Ott U.A generalization of a cyclotomic family of partial difference sets given by Fernández-Alcober,Kwashira and Martínez[J].Disc.Math.,2016,339:2153–2156.
[18]Zhang Yuan,Lei jianguo,Zhang Shaopu.A new family of almost difference sets and some necessary conditions[J].IEEE Trans.Inform.Theory,2006,51:2052–2061.
[19]Zheng Luliang,Lin Liying,Zhang Shengyuan.Constructions of almost difference set pairs by cyclotomy[J].J.Math.,2014,34:116–122.
一类新的部分差集以及分圆数的新性质
张 媛,彭 茂
(南京信息工程大学数学与统计学院,江苏南京 210044)
本文研究了分圆理论与部分差集,强正则图的关系.利用分圆方法,构造了一类新的部分差集,并反过来得到了分圆数的一些新性质.
部分差集;分圆数;强正则图
O157.2
05B10
A
0255-7797(2017)06-1207-08
date:2017-01-16Accepted date:2017-04-26
Supported by National Natural Science Foundation of China(11401317).
Biography:Zhang Yuan(1979–),female,born at Shijiazhuang,Hebei,lecturer,major in combinatorial designs.

