对偶锥映像上的问题

张创亮

(广东工业大学应用数学学院,广东广州510520)

对偶锥映像上的问题

张创亮

(广东工业大学应用数学学院,广东广州510520)

本文研究了对偶锥映像上的一些非线性问题.利用拓扑度理论和半序的方法,获得了对偶锥映像的锐角原理,Debrunner-Flor不等式和不动点定理的结果.推广了一般单调映像的锐角原理和Debrunner-Flor不等式的一些结果.

对偶锥映像;锐角原理;Debrunner-Flor不等式;不动点

1 引言

近年来,非线性泛函分析在各个方面得到广泛的应用,尤其在处理非线性积分方程方面所用的方法起到了不可忽视作用,在国内外也有不少学者研究这个课题.在郭大均[1]一书中介绍对偶映像的单调性、半连续性、次连续性等;Deimling[2]也介绍一些很好的结果.本文主要针对这些性质的一些问题在对偶锥映像上进行研究,在对偶映像上成立的问题,在对偶锥映像上不一定成立,当然我们更希望可以把对偶映像的大部分性质搬到对偶锥映像上来.

本文总假设E是实Banach空间,E∗表示其对偶空间,本文中的⇀表示弱收敛,⇁表示弱*收敛.

定义1.1[1]如果P⊂E是非空凸闭集,并且满足下面两个条件

(1)x∈P,λ≥0,则λx∈P;

(2)PT(−P)={0}.

则称P是E的一个锥.

用P0表示P的内点集,如果P0非空,则称P是E的一个体锥.如果任意的x∈E都可以表示成x=y−z的形式,其中y∈P,z∈P,则称锥P是再生的.易知P是E的一个体锥,则P是再生的.给定E的一个锥P后,则可在E中的元素引入半序:x≤y,其中x,y∈E,如果y−x∈P.

例1设E=Lp(Ω),p≥1,0＜mes(Ω)＜+∞.令P={ϕ:ϕ ∈Lp(Ω),ϕ(x)≥0},显然P是Lp(Ω)的一个锥,但不是体锥.

定义1.2[2]设E是实Banach空间,P⊂E,则P∗={x∗∈E∗:x∗(x)≥0,∀x∈P},则称P∗为P的对偶锥.

令A:P→P∗,称A是对偶锥映像.很显然,对偶锥映像只是对偶映像T:E→E∗的一种特殊情况.不难知道对偶锥可能不是对偶空间上的一个锥.易知P是再生锥,可得P∗是一个锥.事实上,只需验证P∗T(−P∗)={0∗}即可,其中0∗表示零元素.

例2设E=R2,P={(x,y):x≥0,y=0},则P∗={(u,v):u≥0,v∈R}不是E∗=R2的一个锥,但它是P的对偶锥.

定义1.3[1]设E是实Banach空间,P⊂E是一个锥,P∗为P的对偶锥,若映像A:P→P∗,

(1)设x0∈P,A在x0处次连续,是指若xn∈P,xn→x0,则Axn⇀Ax0.若A在P中每一点都次连续,则称A在锥P上次连续.

(2)设x0∈P,A在x0处半连续,是指若h∈E,xn∈P,tn＞0,x0+tnh∈P,tn→0+,则Axn⇁Ax0.若A在P中每一点都半连续,则称A在锥P上半连续.

显然,A在x0处次连续⇒A在x0处半连续.反之不成立.

定义1.4[1](1)设E是实Banach空间,P⊂E是一个锥,P∗为P的对偶锥,若映像A:P→P∗,若A称为在P上单调,是指(Ax−Ay,x−y)≥0,∀x,y∈P.

(2)若A称为在P上极大单调,是指(Ax−f,x−y)≥0,∀x∈P⇒y∈P,f(y)∈P∗.

多值映像A:P→2P∗叫做单调的,如果它的图像G(A)={[x,y]:x∈P,y=Ax}是P×P∗中的单调集.A:P→2P∗叫做极大单调的,如果它的图像G(A)是P×P∗中的极大单调集.

定义1.5[3]设E是实Banach空间,P是一个锥,对x,y∈P{0},令

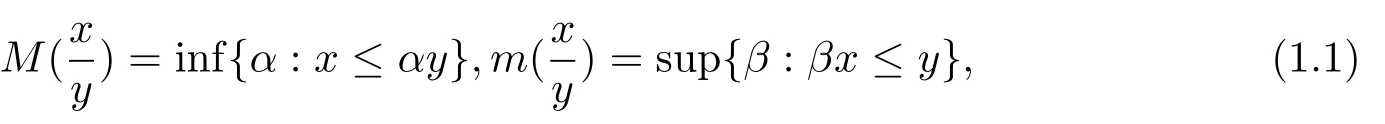
其中inf(∅)=+∞,sup(∅)=−∞.易知对上述非空集合有关系式

现在给Hibert投影距离的定义

定义1.6设E是实Banach空间,P⊂E是一个体锥,P∗是一个锥,若映像A:P0→P∗{0∗},∀xn,x0∈P0,n=1,2,···,ρ(xn,x0)→0,则ρ(Axn,Ax0)→0,称A在x0处Hilbert投影距离连续.

定理1.1[1]设E是自反实Banach空间,映像T:E→E∗半连续、单调.又设对于某个r＞0,有

其中Ωr={x:x∈E,‖x‖＜r},那么方程Tx=0∗在中必有解.

定理1.2[1]设E是实Banach空间,K是E中紧凸集,G⊂K×E∗且G是单调集.又设T:K→E∗是连续映像,h∈E∗.于是,必有u∈K存在,使得

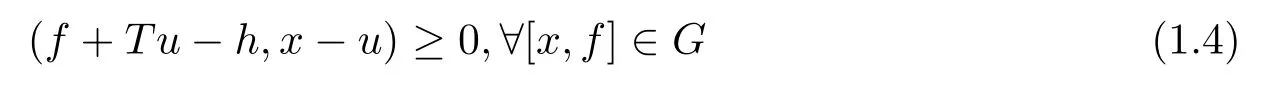
2 主要结果

引理2.1设E是自反实Banach空间,P⊂E是一个体锥,P∗为P的对偶锥,若映像A:P→P∗单调的,那么A在x0∈P0半连续且局部有界⇒A在x0处次连续.

[1,2]共轭映像上类似的证明方法就可得到引理2.1.

引理2.2[4]设E是赋范线性空间,X是E的凸子集,若X是闭的当且仅当它是弱闭的.

下面定理是对定理1.1推广到对偶锥映射上.

定理2.1设E是自反实Banach空间,P∗为P的对偶锥,若映像A:P→P∗次连续、

单调.设任意r＞0,使得则Ax=0∗在有解.

证由引理2.2可知有界弱闭集,对任意的x∈P,令

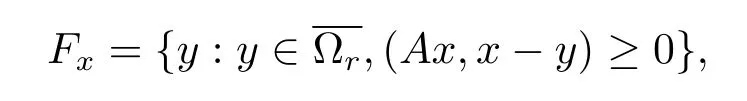
很显然Fx是弱闭集,任取x1,x2,x3,···,xm∈P,则事实上,不妨令

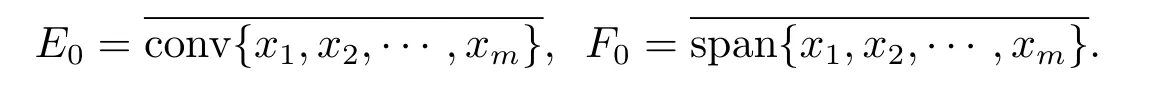
易知E0是至多m维向量闭子空间F0的闭凸子集,定义映像T:E0→F0,其中

由于假设可知A是E0上次连续,从而可得T:E0→F0是连续的,令

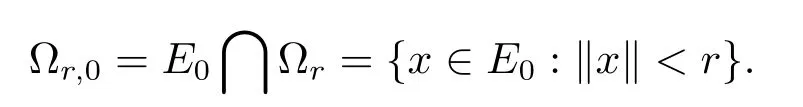
现在先证明Tx=0在中必有解,若0/∈Tx,则由Brouwer度deg(T,Ωr,0,0)=0,但 deg(I,Ωr,0,0)=1,其中I为恒等映射.因此A与I在Ωr,0不同伦,从而存在x0∈∂Ωr,0,0＜t0＜1,使得t0Tx0+(1−t0)x0=0,即则有

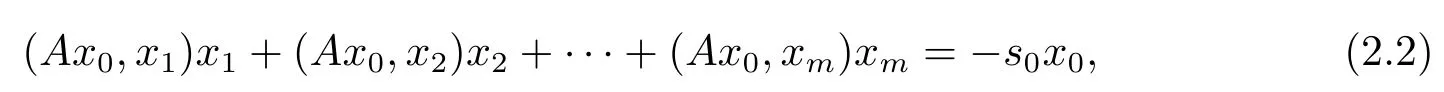
在式子(2.2)两端左边同时作用Ax0得到

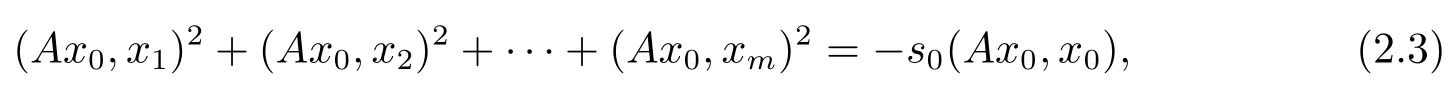
由于(Ax0,x0)≥0,因为x0∈ ∂Ωr,0⊂P,故(Ax0,xi)=0,i=1,2,···,m,由(2.2)式可以知道x0=0,这与x0∈∂Ωr,0矛盾.这就得出了Tx=0在中有解即

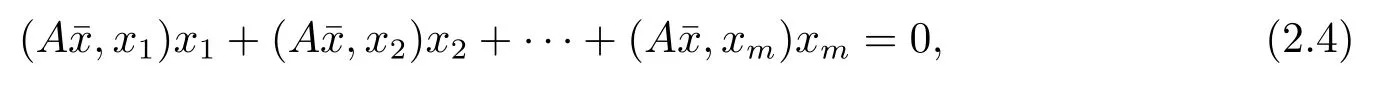
由于对偶锥的性质和xi≥0,从而可以得到()=0,i=1,2,···,m,现任取x∈E0,那么有其中,α≥0,j=1,2,···,m,则()=0,又0,从而此时注意到A的单调性

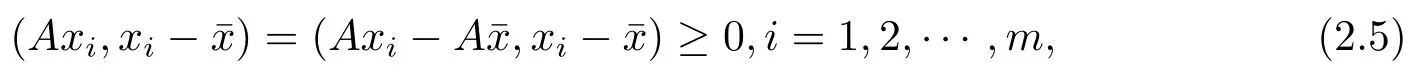
令t→0+,可得

故Ay=0∗.

推论2.1设E是自反实Banach空间,P⊂E是一个体锥,P∗为P的对偶锥,若映像A:P→P∗半连续、单调的,∂P是连续的,在P0处局部有界.设任意r＞0,使得则Ax=0∗在有解.

证由引理2.2可知有界弱闭集,对任意的x∈P,令

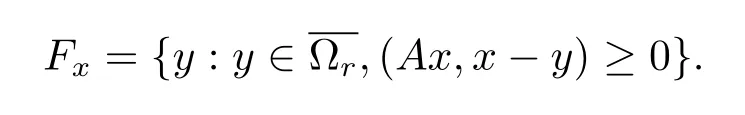
很显然Fx是弱闭集,任取x1,x2,x3,···,xm∈P,要证令

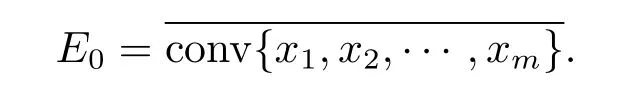
定义Tx=(Ax,x1)x1+(Ax,x2)x2+···+(Ax,xm)xm,x∈E0,由于A在P0处半连续且局部有界,由引理2.1可知A在P0是次连续,又A在∂P是连续的,从而可知T在E0上连续.接下来按照定理2.1证明即可.

注1定理2.1和推论2.1是单调映像锐角原理的推广.

下面来讨论一下著名的Debrunner-Flor不等式.

定理2.2设E是实Banach空间,P是E的一个体锥,K是P中紧凸子集,G⊂K×P∗且G是单调集.又设T:K→P∗是连续对偶锥映像,h∈P∗.于是,必有u∈K存在,使得

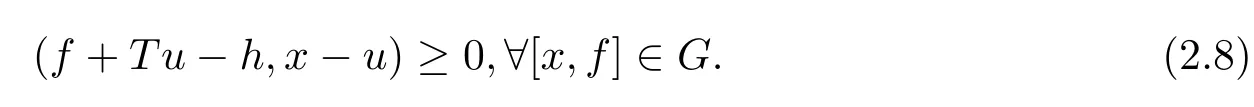
证参考文献[1]的类似证明方法即可.

此外还有有限维空间的Debrunner-Flor不等式和一般空间的Debrunner-Flor不等式在对偶锥映像上是否成立,本文不再谈论,有兴趣的读者可以自行验证.

定理2.3设E是实Banach空间,P⊂E是一个锥,P∗为P的对偶锥,且P∗是一个锥,若映像A:P→P∗是增算子,对任意的x,y∈P,y−x∈P,则(Ax−Ay,x−y)≥0.

证∀x,y∈P,y−x∈P,则有x≤y,又由于A是增算子,那么Ax≤Ay,根据P∗是一个锥,就有Ay−Ax∈P∗,则(Ax−Ay,x−y)≥0.

定理2.4设E是实Banach空间,P是E的一个锥,若A:P→P∗半连续、单调,则T必是极大单调.

证证明方法与文献[2]类似.

引理2.3[3]设E是实Banach空间,P⊂E是一个体锥,对x,y∈P0,ρ(x,y)是P0上的一个拟距离,即满足

(1)x∈P0⇒ρ(x,x)=0,

(2)x,y∈P0⇒ρ(x,y)=ρ(y,x),

(3)x,y,z∈P0⇒ ρ(x,y)≤ ρ(x,z)+ρ(y,z).

另外易知

(4)x,y∈P0,α ＞0,β ＞0⇒ ρ(αx,βy)=ρ(x,y),

(5)ρ(x,y)=0⇔x=αy,其中α＞0.

令P1=P0T{x:x∈E,‖x‖=1},于是由(5)知(P1,ρ)是一个距离空间.

(6)设范数关于单调的(即0≤x≤y⇒‖x‖≤‖y‖),则(P1,ρ)是完备的距离空间.

当P∗是体锥时也有上面类似结果.

注2若P是一个体锥,其中表示锥P∗的内点集且非空,一般会认为利用完备的度量空间和Banach压缩映像原理可以得出A有不动点,这种想法显然不对,因为A是将P1中元素映射成共轭空间上的泛函,不是P1本身的元素,若E是Hilbert空间,则上述的想法是对的,因为每个Hilbert空间的泛函就是它本身,一般情况下,我们比较感兴趣的是Banach空间上的性质,以致下面定理为了得到不动点,引入了线性算子作用在共轭空间上.

定理2.5设E是实Banach空间,P⊂E是一个体锥,设范数关于P单调的,P∗是一个体锥,A:P0→P0∗是正增p齐次的,0＜p＜1,j:P∗→P0是增的线性算子,则jA在P0中必有唯一的不动点.

证假定0＜p＜1,由和A的增正p齐次性知

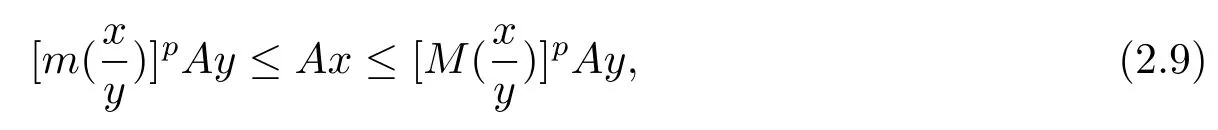
由于j是增线性算子

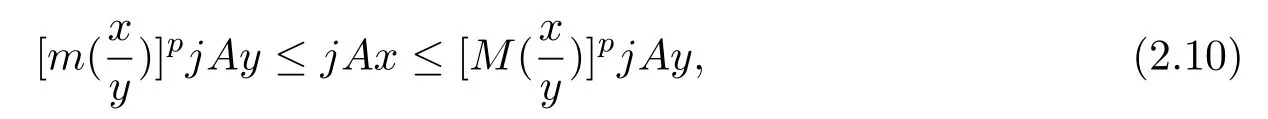
那么

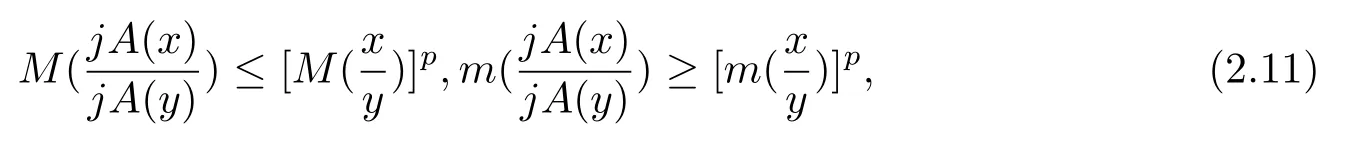
根据Hilbert投影距离的定义知

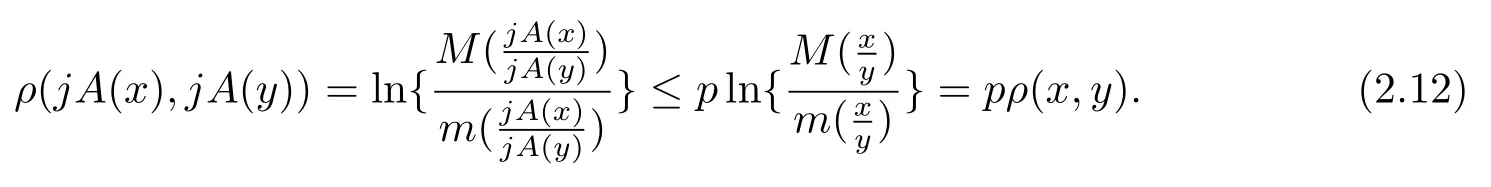
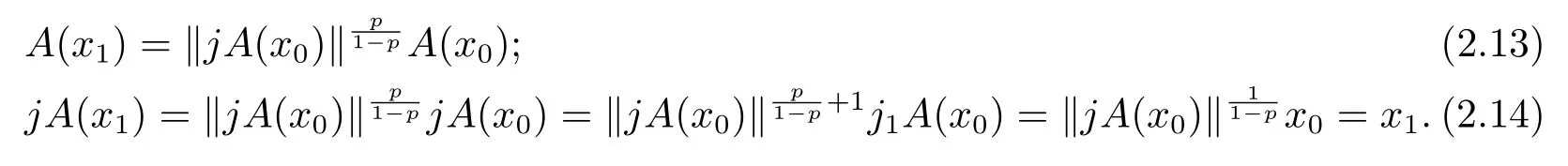
故jA在P0中有不动点x1.现在证明它的不动点是唯一的,假设它还有另一个不动点x2,jA(x2)=x2,因

可知

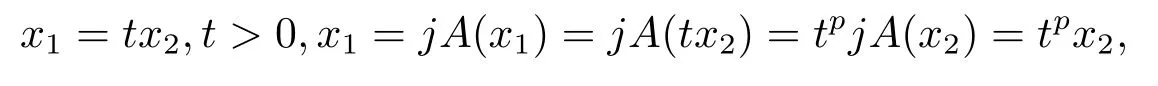
则可以推出t=1,即是x1=x2.

注3在这里取P=P∗,此时在这里的线性增算子定义j=I为恒等算子,此时只需要讨论A:P0→P0,这个结果在文献[1]中可以查阅.

若应用注3里面的条件,就会有下面例子的成立.

例3设非线性积分方程其中0＜p＜1,f(x,y)在G×G非负连续且表示Rn中某有界闭区域,那么非线性积分方程在G上具有唯一的恒正连续解.

当知道P和P∗是一个体锥,假设A:是p正齐次的,0＜p＜1,并且是增的,得出A在P1上是一个Hilbert投影距离连续算子.

事实上,假定0＜p＜1,∀x,y∈P1,由A的增正p齐次性知

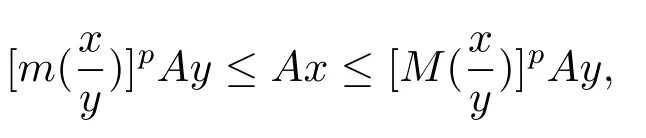
则

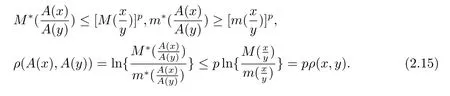
若∀x,y∈P1,ρ(x,y)→0,则ρ(Ax,Ay)→0,即是A在P1上Hilbert投影距离连续.显然Hilbert投影距离连续并不能推出依范数连续.

首先思考当Hilbert投影距离连续时要满足什么条件就可推出依范数连续,反之也是否能成立,下面定理就是所要讨论的结果.

定理2.6设E是实Banach空间,P和P∗是一个体锥,范数分别关于P和P∗单调的,映像A:若A在P1上Hilbert投影距离连续,则它是依范数连续.

证任意取xn,x0∈P1,使得又因由于范数关于P单调的,则

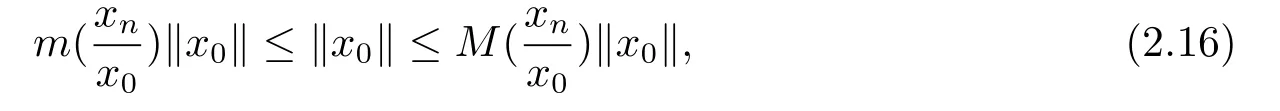
即是

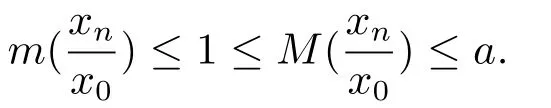
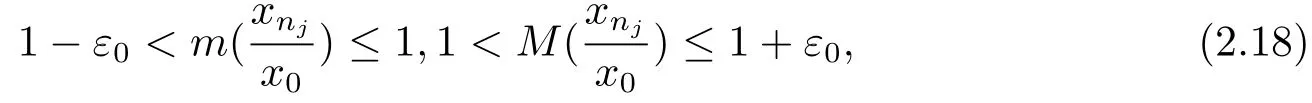
故当n＞N时,恒有

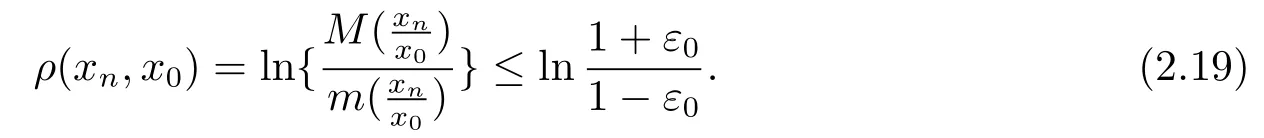
由任意的ε,可以知道由假设映像A:是Hilbert投影距离连续,对上面的ρ(xn,x0)→0,则ρ(Axn,Ax0)→0.当若对有由于范数关于P∗单调的,则

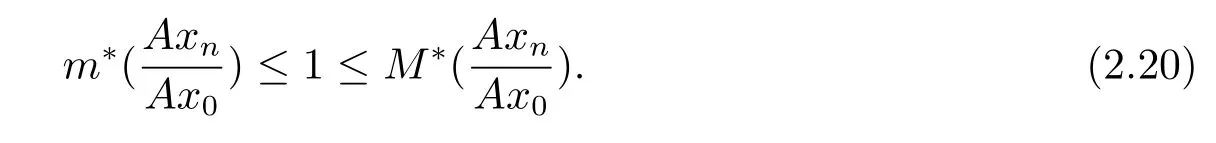
那么

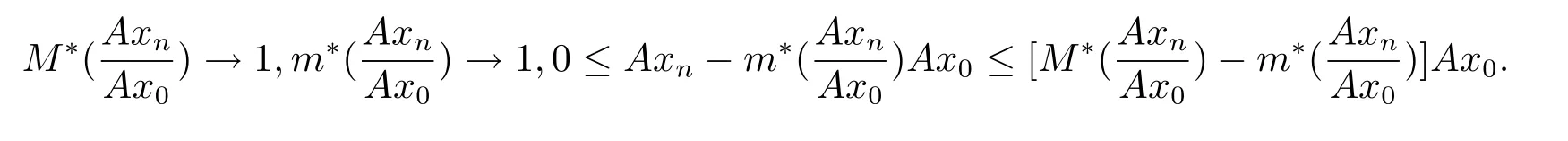
故

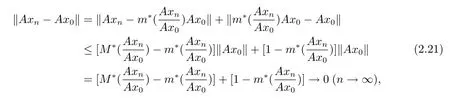
故A在P1上依范数连续.

定理2.7设E是实Banach空间,P和P∗是一个体锥,范数分别关于P和P∗单调的,映像A:若A在P1上是依范数连续,则它是Hilbert投影距离连续.

证若对取xn,x0∈P1使得ρ(xn,x0)→0,根据定理2.6的证明可以知道‖xn−x0‖→0,由假设A:是依范数连续,故接下来同样按定理2.6类似证明可以得出ρ(Axn,Ax0)→0.

注4由定理2.6,定理2.7可以知道当P和P∗是一个体锥,范数关于P和P∗单调时,可以得出映像A:是Hilbert投影距离连续与依范数连续等价.

参考文献

[1]郭大均.非线性泛函分析(第3版)[M].北京:高等教育出版社,2015.

[2]Deimling K.Nonlinear functional analysis[M].Berlin:Springer Press,1985.

[3]Bauer F L.An elementary proof of the Hopf inequality for positive operators[J].Numer.Math.,1965,17:331–337.

[4]Conway J B.A course in functional analysis(2nd ed.)[M].New York:Springer Press,1990.

[5]Chen Y Q,Cho Y J.Monotone type operators in nonre fl exive Banach space[J].Fixed Point Theory Appl.,2014,2014:119.

[6]梁展东.Hilbert投影距离与范数的关系[J].系统科学与数学,1988,8(1):88–91.

[7]Browder F E.Degree of mapping for nonlinear mappings of monotone type[J].Proc.Nat.Acad.Sci.USA,1983,80:1771–1773.

[8]魏利,刘元星.Banach空间中m−d增生映射零点的强弱收敛定理[J].数学杂志,2016,36(3):573–583.

[9]崔玉军,邹玉梅.非线性算子的歧点[J].数学杂志,2011,31(3):476–480.

PROBLEMS OF DUAL CONE MAPPING

ZHANG Chuang-liang
(College of Applied Mathematics,Guangdong University of Technology,Guangzhou 510520,China)

In this paper,we study some nonlinear problems of dual cone mapping.By using topological degree theory and partial order methods,we get the results of the acute angle principle,Debrunner-Flor inequality and fixed point theorem for dual cone mapping.Some results in the document are improved and extended.

dual cone mapping;acute angle principle;Debrunner-Flor inequality; fixed point

47H05;47H07

O177.91

A

0255-7797(2017)06-1245-08

2016-09-27接收日期:2017-04-19

国家自然科学基金资助(11601093).

张创亮(1992–),男,广东梅州,硕士,主要研究方向:非线性泛函分析.