基于SUE模型的区域交通配流问题

吴兴宇，刘 雅，王陈炜，王志勇

·创新创业技术——数学建模·

基于SUE模型的区域交通配流问题

吴兴宇，刘 雅，王陈炜，王志勇

(电子科技大学 数学建模实验中心，四川 成都 611731)

该文引入Akamatsu提出的SUE改进模型，用以计算一定交通总流量下分配到各个路段的道路流量。出于对不同类型小区的考虑，对交通配流模型的参数进行了改进。针对增加的交叉路口对车速的影响，对最终的流量计算和速度计算公式进行了修正。使用修正后的交通配流模型，采用泊松分布模拟闲期数据和二项分布模拟高峰期数据，对 “日”字形、“田”字形和 “花纹形”3种类型的小区进行道路流量的求解。仿真结果表明，不同的小区结构会导致不同的开放效果，如 “田”字形小区开放造成新开道路的拥堵，使得 “田”字形小区没有开放的必要。

SUE模型； 交通流； 模拟退火算法； 小区开放

根据国务院最新发布的关于推广街区制的意见，小区逐步开放成为一个时下社会讨论的热门话题。开放小区有利有弊，好处在于可以缓解当下大中型城市普遍存在的交通拥堵问题，利于改善道路通行能力、优化路网结构等[1]。而开放小区也存在一些弊端，如小区的安全问题、开放小区会导致干路车辆增多、影响通行速度等。与此同时，在开放小区政策的实施中，需要考虑诸多因素，如小区的面积、位置、外部及内部道路状况等[2-3]。

为了对小区开放问题进行科学合理的决策，本文将从以下3个方面通过建立数学模型并仿真计算，探讨小区开放的合理性问题。

1)提出评价指标体系，评价小区开放对周边道路通行的影响；

2)建立描述车辆通行的数学模型，对小区周围道路交通情况进行仿真；

3)分析不同类型的小区，用仿真结果说明其开放对道路通行的影响。

1 道路通行影响的评价指标

为了评价小区开放对周边道路通行的影响，我们建立了小区周边路况的评价指标体系，该体系包括道路通行饱和系数与路网密度两个指标。前者分析的是每条道路的具体情况，反映了每条道路车流量负载的饱和程度；后者分析的是整个道路网体系，反映了小区所在区域道路网铺设的密集程度。

1.1 道路通行饱和系数

道路通行饱和系数是指道路实际通行车辆(通行车辆实际值)与道路最大通行能力(通行车辆理论值)之间的比值，反映了每条道路车流量负载的饱和程度。道路单位时间通行量指的是某一条道路的路口位置截面在单位时间(一个小时内)的范围内通过的车辆数。此指标刻画了道路的畅通程度，表征某一条确定道路对车辆的输送水平。

首先计算道路的理论通行能力，理论通行能力的求解公式如下[4]:

式中，N表示通行能力，veh/h；v表示行车速度，m/s；V表示各道路标准行车速度，km/h；L表示车头间距，m，由车长、司机反应时间的行驶距离、制动距离差和安全距离共同决定，其计算方法为:

式中，l1表示汽车长度；vt表示汽车司机在反应时间内汽车行驶的距离；v表示车速；t表示反应时间，通常取值为1～1.8 s；l2表示车辆间的安全间距，可取2～5 m；s表示刹车后的制动距离，其计算公式为:

式中，K2表示后车刹车安全系数，K1表示前车刹车安全系数，两者之差通常取0.67；ψ表示轮胎与路面间的附着系数，通常取0.2～0.5；f表示滚动阻力系数，通常取0.02；i表示道路纵坡，上坡取正号，下坡取负号。

因此，道路通行饱和系数，即为通行量的实际值与理论值之比的计算公式为:

式中，N/N′表示道路的单位时间通行量。

1.2 路网密度

路网密度包括道路网密度和干道网密度，是度量某已确定区域道路网结构的一个参数。道路网密度指的是区域道路总长度与区域用地总面积之比(km/km2)；干道网密度指的是区域主次干道总长与区域用地总面积之比 (km/km2)。

根据道路网密度和干道网密度的定义可知，两个系数的计算公式为:

式中，δ和δg分别表示道路网密度和干道网密度，S表示所分析的区域 (小区所在区域)的建成面积，Li和Lj分别表示区域所有道路和区域主干道。

2 交通流分配模型的建立

2.1 BPR函数

在交通规划四阶段的交通分配阶段，要对交通流量进行分配，就要考虑到某一路段的时间阻抗。对于路段行驶时间的修正，可以根据行驶时间和路段交通量之间的关系，即路阻函数确定。最为常见的路阻函数是美国联邦公路局函数(BPR函数):

式中，ij表示从路段i到路段j，也可以理解为从路段i的路口节点到路段j的路口节点之间的所有通行关系；tij表示路段ij上的走行时间(s)，也即路阻抗函数的主体；αij表示在ij路段上的自由流走行时间(s)；fij表示路段ij上的流量(veh/h)；βij表示在ij路段上的延误参数，其计算公式为[5]:

式中，δ取0.15，γ取4；Vij和Cij的比值表示理想状况下最大服务量和基本通行能力之比。

2.2 基于SUE的交通流分配模型

以上述改进的BPR函数为基础，下面将建立交通流的分配问题，用以研究小区周边道路的交通流在不同时间的车流量情况及小区开放以后车流量在新道路上的分配演变。

定义网路G＝(N，A)，其中，N、A分别为节点和路段集合，O、D分别为起点和终点集合。其中，o表示任意起始节点，d表示任意终止节点，xji表示路段(i，j)∈A的流量，xoij表示由某一起点O流入路段(i，j)的流量，qod表示起点和终点o、d之间的交通需求。

Akamatsu对传统的基于Logit的SUE模型的熵项进行了分解，得到基于路段变量的SUE模型[6-7]，该模型以所求解的地区各个路段的交通需求量为基础，即可为一个交通网路中各个路段合理分配交通流，其模型公式为:

式中，约束条件的第一个公式表示任意路段增加的通行流量等于该路段实际需求流量，第二个公式限制了每一个路段对其他路段输送的流量为正值。目标函数中的Z为Akamatsu在文献[7]中提出的一个优化目标，在该目标达到最小的时候即可得到最合理的交通流分配结果。公式中tij(f)为BPR函数，其所对应的积分公式在实际计算中是一个简单的二次函数。δok和δdk为开关函数，当k＝o、d时，δok或 δdk＝1； 否则， 等于 0。 HL(xo)和 HN(xo)由下列公式计算:

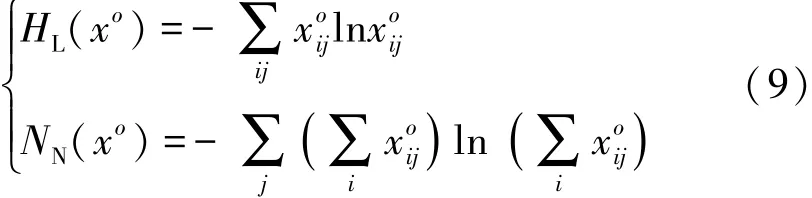
由于SUE模型是求解理想的道路情况，并没有考虑道路的最大通行能力，在现实世界中，不会出现道路上的车流达到甚至高于道路设计容量的情况，当出现此类情况时，道路是被 “过度使用”，相应的其他道路本该分配到的流量会减少，这种情况，对于规划者做出科学合理的分析是不利的。所以需要在模型中加入容量约束，以优化分配结果。并且考虑到拥堵至一定情形时，用户不会继续驶入，所以加入容忍系数的概念。因此，有约束条件如下:

式中，ρij表示路段ij的容忍系数，因为通行饱和度在0.85以上时会体现出道路拥堵现象，故建议取值为0.85～0.9。

2.3 用交通流量估计平均车速

通过上述模型求解而得到的每一路段交通量，我们可以代入经典的速度流量模型求解出路段的平均速度。速度流量模型在HCM[8-9]中使用，其求解公式为:

式中，vf表示畅行车速，即车流密度趋于0时车辆畅行无阻时的空间平均车速，kj表示阻塞密度，为车流密集到车辆无法移动时的密度。

3 交通流分配模型的改进

小区开放以后，将会有若干条道路加入该区域的交通网，新道路与原主干道之间的连接处，由于其功能和位置上的特殊性，将会影响主干道上的车流速度。穿行小区的道路，考虑到小区住户的安全性问题，必然会限制车速而使得平均车速小于干道的平均速度，并且车流在支路向干路汇集的时候，将会因为交通信号灯、转弯减速等原因而降低行车速度，从而对干路的车速产生影响。分析种种原因，都会产生时间上的延迟。本文中采用交叉口平均延误计算方法[10]，其公式为:

式中，T表示信号周期长度，s；tg为有效率绿灯时间，s；x表示车道组V/C或饱和度，V/C指在理想条件下，最大服务交通量与基本通行能力之比。

这一延迟将会减小道路的流量和通行速度，减小的比例通过理想车速通行道路的时间和交叉口延迟时间的关系来确定。流量和通行速度的公式为:

式中， x′ij和 v′ij路段的道路流量和通行速度， xij和 vij表示修正前ij路段的道路流量和通行速度，lij/vij表示未修正时通行道路的时间[11-12]。

4 仿真结果

4.1 “日”字形开放格局

图1 “日”字形和 “田”字形开放格局示意图

如图1(a)所示，为广州市某小区群的地图。图中主干路已经使用黑线表示，将开放的小区支路用红线表示。从道路结构和小区结构的角度考虑，开放后的格局可以等效的看成一个 “日”字形结构，下面对其开放前后的参数进行计算，并对开放可行性进行分析，如表1所示。

表1 “日”字形开放格局计算结果

1)从交通流量的变化情况来看，该路段交通流量基本流向新开路段EF，交通流量较大的AB和CD路段，其压力得到明显的缓解，运输压力较小的BC、AD路段较开放前的交通流量也有所下降；

2)从车流速度的变化情况来看，各路段车流速度均增大，但AB和CD道路受到新开路段EF交叉路口的小车速影响，增长不明显；

3)从饱和系数的变化情况来看，开放前处于拥堵水平的AB、CD路段在开放后均下降为正常水平，其余路段也有明显的下降趋势，可见开放EF路段对道路的交通流量的分担作用明显。

综上分析，在车流总量为5 992 veh/h的前提下，这里的 “日”字形小区有开放的必要性，有助于缓解部分路段的拥堵问题。

4.2 “田”字形开放格局

如图1(b)所示，为广州市某小区群的地图，其开放后的格局等效为 “田”字形结构，下面对其开放前后的参数和指标进行计算，并对开放可行性进行分析，如表2所示。

表2 “田”字形开放格局计算结果

1)从交通流量的变化情况来看，该路段最大交通能力相差不大，其交通流量的差异主要源自于交通需求量的差异，在开放前后，主干路的交通流量都显著减少，并且流向了EG和HF，然而，由于道路EG的道路通行能力较低，开放后使得交通流量接近饱和；

2)从车流速度的变化情况来看，各路段车流速度均增大，但是新开路段EG的车速过小，可能出现拥堵情况；

3)从饱和系数的变化情况来看，开放前处于拥堵水平的AB、CD路段在开放后均下降为正常水平，其余路段也有明显的下降趋势。然而，新开路段EG处于拥堵水平，不利于缓解交通压力。

综上分析，在总车流量为4 645 veh/h的前提下，这里的 “田”字形小区中，道路EG没有开放的必要性，考虑到不开放EG会使原本由EG分担的流量流向HF，而HF在当前状态也不在畅通状态下，很可能会导致较为拥堵的情况出现，因此，这里的道路没有开放的必要，主要原因在于新开路段的通行能力太小。

4.3 花纹形开放格局

图2 花纹型开放格局示意图

如图2所示，为我们构造的一个小区道路图，开放后的格局可以等效的看成一个花纹形结构，下面对其开放前后的参数进行计算，并对开放可行性进行分析，如表3所示。

1)从交通流量的变化情况来看，该路段交通流量基本流向新开路段，原本交通流量较大的AB和AD路段，其运输压力得到明显缓解，运输压力较小的路段较开放前的交通流量也有所下降；

2)从车流速度的变化情况来看，各路段车流速度基本增大但幅度不明显，其原因在于道路交叉路口的复杂性使得车速受到明显影响，即使在交通流量明显减弱的情况下，车速提高仍不明显，甚至下降；

3)从饱和系数的变化情况来看，开放前处于拥堵水平的AB、AD路段在开放后均下降为正常水平，其余路段也有明显的下降趋势，可见开放4个路段对道路的交通流量的分担作用明显。

综上分析，在总车流量为3 840 veh/h的前提下，这里的花纹形小区有开放的必要性，有助于缓解部分路段的拥堵问题，但是由于新增路口汇集到主干路，这一位置的复杂性影响了小区开放的交通实效。

5 结束语

本文选取了合适的指标体系分析并评价小区开放对道路通行的影响，在此基础上建立了基于SUE模型的区域交通配流模型，并分析了不同类型的小区开放前后对周边道路通行的影响。通过数据结果不难发现，不同的小区开放后的效果是不一样的，部分小区会对区域的交通压力有所缓解，而另一些小区则可能会产生负面影响，因此，在实际决策中，决策者应该根据小区周围的道路及其对应的车流量，结合早晚高峰的拥堵情况，应用本文模型进行仿真，在开放或不开放中做出恰当的选择。

[1]SHANKAR V，MANNERIINGF.Modeling the endogeneity oflane-mean speeds and lane-speed deviations:a structuralequations approach[J].Transportation Research Part A Policy＆ Practice，1998，32(5):311-322.

[2]CASTILLO JM，BENITEZ F G.On the functional form of thespeed-density relation-ship-II:empirical investigation[J].Transportation Research Part B Methodological，1995，29(5):373-389.

[3]WU N.A new approach for modeling of fundamentaldiagrams[J].Transportation Research Part A Policy＆ Practice，2002，36(10):867-884.

[4]李冬梅，李文权.道路通行能力的计算方法[J].河南大学学报(自然版)，2002，32(2):24-27.

[5]郑远，杜豫川，孙立军.美国联邦公路局路阻函数探讨[J].交通与运输(学术版)，2007(1):24-26.

[6]AKAMATSU T.Decomposition of path choice entropy in general transport network[J].Transportation Science，1997，24(1):58-62.

[7]AKAMATSU T.Decomposition of path choice entropy in general transport network[J].Transportation Science，1997，24(1):58-62.

[8]WASHINGTON D.Highway capacity manual[J].Special Report， 2000， 1(1):5-7.

[9]IBRAHIM A T，HALL F L.Effect of adverse weather conditions on speed-flow-occupancy relationships[J].Transportation Research， 1994， 2(5):34-56.

[10]任福田，刘晓明，宋建.交通工程学[M].北京:人民交通出版社，2008.

[11]景春光，王殿海.典型交叉口混合交通冲突分析与处理方法[J].土木工程学报，2004，37(6):97-100.

[12]王进，唐忠华，陆化普.车辆折算系数研究[J].土木工程学报，2004，37(12):97-102.

Regional Traffic Assignment Problem Based on SUE Model

WU Xingyu， LIU Ya， WANG Chenwei， WANG Zhiyong
(Mathematical Modeling Experiment Center， University of Electronic Science and technology of China， Chengdu 611731， China)

This paper introduces the SUE improved model proposed by Akamatsu to calculate the road traffic allocated to each section under certain traffic flow.For the consideration of different types of distracts，we improved the parameters of traffic distribution model.The final flow calculation and velocity calculation formula are modified for the effect of the increased intersections on the vehicle speed.Using the modified traffic distribution model， the Poisson distribution was used to simulate the idle data， and the binomial distribution was to simulate the peak flow data.The road traffic was solved in three types distracts of“Ri”， “Tian” (Chinese word)and“Pattern” .The simulation results show that different community structure will lead to different open effects， for example， “Tian”structure community causes the new road congestion，which makes the filed structure community is not necessary to open.

SUE model； traffic flow； simulated annealing algorithm； community open

U412

A

10.3969/j.issn.1672-4550.2017.05.001

2017-04-07；修改日期:2017-06-07

国家自然科学基金(11301058)；中央高校基本业务费(ZYGX2015J103)。

吴兴宇(1996-)，男，本科生，计算机科学与技术专业。

王志勇(1980-)，男，博士，副教授，主要从事随机微分方程数值解方面的研究，zhywang＠uestc.edu.cn