深水多波束声呐测深数据精度评估

张国堙，陶春辉，王奡，3，邓显明，何拥华

(1.国家海洋局第二海洋研究所，浙江 杭州 310012；2.国家海洋局海底科学重点实验室，浙江 杭州 310012；3.中国地质大学(武汉) 地球物理与空间信息学院，湖北 武汉 430074)

深水多波束声呐测深数据精度评估

张国堙1，2，陶春辉1，2，王奡1，2，3，邓显明1，2，何拥华1，2

(1.国家海洋局第二海洋研究所，浙江 杭州 310012；2.国家海洋局海底科学重点实验室，浙江 杭州 310012；3.中国地质大学(武汉) 地球物理与空间信息学院，湖北 武汉 430074)

多波束测深精度评估是水深测量质量控制的重要方面，静态精度评估与交叉测线动态精度评估能够从不同角度表征测深精度，估计测量样本的综合误差。在实际调查作业过程中，由于缺少水深真值，在进行精度估计时缺少可操作性。本文利用Kongsberg EM120型深水多波束系统的测深数据，基于某一区域的重复测量数据，应用中央波束的水深数据进行静态精度分析；通过引入网格化方法，进行动态水深精度评估分析，并通过偏差分析揭示测量样本的误差分布特征。结果表明，中央波束水深数据静态精度评估与基于网格化方法的动态精度评估具有实际可操作性，其结果能够有效估计测深的综合误差；重复测量数据的偏差分析能够有效展示误差的分布特征。

多波束声呐；精度评估；误差分析

1 引言

海洋水深测量是进行科学研究、资源勘查以及大陆架划界等的基础性工作，多波束声呐是目前开展大面积水深测量的主要手段，也是国际海道测量组织(International Hydrographic Organization， IHO)规定的在高级别水深测量中必须采用的技术[1]。多波束声呐获得的水深值包含了多种因素带来的测量误差，其测量值只能无限逼近真值，但不等于水深真值，对测量值进行精度评估是进行水深测量质量控制的重要手段。测量精度是表征测量误差的指标，应用精度表征测量值与真实值之间的偏差，具体描述测深的误差，表征水深真值的范围，对于水深测量的质量控制具有重要意义。

精度是对误差的估计，多波束声呐是由多个传感器构成的组合测量系统，测量误差来源于系统的多个方面，其水深测量精度的评估包含了各方面误差的综合影响。目前，尚未有比多波束测深系统更高数量级精度的测深设备诞生，即难以使用另一种专门的更高精度的测量器具来评估多波束系统的水深测量精度；另外，在水下建立高精度的测量控制点比较困难，因此，对多波束声呐测深的绝对精度评估难以实现[2]。国际海道测量组织为了规范测量数据具有足够精度，根据不同的测量等级，制定了相应的精度容限要求。我国在《海洋调查规范：海底地形地貌调查》(GB/T 12763.10-2007)中，要求多波束测深作业须布置垂直于主测线的检查测线，利用冗余数据进行数据质量控制，具体开展数据精度评估，可利用定点法、重复测线法、交叉测线法和相邻测区拼接的重叠区的重合点水深数据进行比对[3]。在行业标准《海洋多波束测量技术规程》(DZ/T 0292-2016)中，使用均方根误差(Root Mean Square Error， RMSE)计算水深测量准确度，分别对定点测量、平行测线以及交叉测线的准确度计算作了相关规定[4]。目前，海洋水深测量的技术指标存在较大的模糊性，对实际测量作业没有全面的参考意义[5]。多波束测深的误差分析与精度评估一直受到学者们的关注，朱庆和李德仁[6]系统分析了多波束测深数据的误差来源，并开展了相关的误差改正处理模型，以保证测深系统必要的精度；李家彪等[7]探讨了多波束测深的精度影响因素，并提出了控制精度改正的措施；吴自银等[8]分析了不同误差对测量精度的影响并进行了综合校正；陈非凡[9]提出了一种多波束测深动态测量误差评估方法，应用了相对误差的指标开展了分析；李宜龙等[10]针对描述精度的数理统计指标进行了分析；吴英姿等[11]对交叉测线重叠区域的数据从不同层面进行了统计分析处理；吴超等[12]基于IHO规范的不确定度指标分析了多波束测深数据的质量评估方法，讨论了各分量精度对测量结果的影响；高君等[13]通过设计具体的检定系统，进行了精度评估试验；马延霞[14]从具体理论上对精度评估进行分析，开展模拟仿真研究，讨论多波束测深的相对精度和绝对精度的系统精度评估方法；杨广义[15]针对基于多波束测深数据建立的海底数字地形模型，开展精度评估研究，优选地形建模算法；唐秋华等[16]应用不同的多波束测深系统进行测深精度比较分析，基于均方根误差开展内符合与外符合精度评估研究；肖波等[17]应用均方根误差，分别针对定点与重复测量区域进行了精度评估研究；黄辰虎等[18]针对不同的误差源，建立了质量评价指标；总之，国内对多波束测深误差的来源以及改正方法进行了深入研究并有较为完善的方法，在精度评估方面开展了多层次的探讨，较多地使用均方根误差作为精度指标进行分析研究[16-17]，但并未形成完善统一的方法。国外学者也使用均方根误差表征精度，并且具体针对不同波束范围内的测深精度进行了评估[19]；对多波束声呐测量的水平定位与垂直测深精度进行联合评估[20]；较早对多波束测深的误差来源进行了深入研究，并推导了总传播误差[21]；应用船舶在动力定位状态下，保持艏向不变，采集多波束静态水深数据，对比分析不同性能指标的运动传感器与深度误差的相关性[22]；通过与单波束测深数据进行比对分析，探讨多波束测深的绝对偏差，并且比较边缘波束与中央波束的测量精度[23]；基于实际测深数据进行了精度评估分析，并与IHO规范作比较研究[24]；基于IHO规范中的不确定度评估指标，在实际数据质量评估中开展相关的应用研究[25]；对除导航定位、运动传感器以及声速剖面等辅助传感器之外，针对声学测量技术本身的误差评估开展了研究[26]；利用多次重复测量数据，针对水平定位误差与深度测量误差开展了研究[27]。国际与国内均发布了较多的多波束水深测量相关规范以及相关精度评估方法研究，但是对于多波束测量成果精度评估尚未形成一个统一的精度评估模型，并且，大部分测量规范强调了均方根误差的计算，但是对于如何利用均方根误差没有给出进一步的详细说明[28]。目前，通过对仪器本身的多次测量结果进行统计分析是评估其精度的主要手段，即相对精度评估。相对精度评估包含静态精度评估与动态精度评估，静态精度评估即对多波束系统在固定点作业的测深数据进行精度评估，动态精度评估即对多波束系统在动态扫测作业的测深数据进行精度评估。

多波束测深系统最大的特点是其一次测量能够获得上百个测点，多个测点对应不同位置的地形，针对定点静态精度评估，本文应用测量船在开启动力定位时，船舶最大限度保持静态时所采集的多波束水深数据，通过统计分析，获得静态作业状态下的定点测量精度；对于动态测量数据，选取同一区域交叉测线数据，应用相同参数进行网格化处理，获得同一位置的两次测量数据，进行系统动态精度评估。同时，基于IHO测量规范，针对动态测量数据，计算相应测量等级的误差容限，与动态精度评估结果比较，评价测量等级。

2 多波束测深系统的误差来源与测深精度评估指标

2.1 多波束测深系统原理

多波束测深系统的基本原理，是通过同时获得的多个波束在海水中的旅行时和到达角，结合声速剖面，应用斯涅耳法则进行声线跟踪，计算波束脚印在船体坐标系下的水深，再应用实时三维姿态数据和全球导航卫星系统的定位数据，把船体坐标系下的水深点转换到地理坐标系下，最终获得波束脚印对应的水深及其地理坐标。多波束声呐系统一次发射接收声脉冲可以形成上百个波束，即可获得地理坐标系下的上百个水深数据，极大地提高了水深测量的作业效率。在水深的计算过程中，多个传感器参与其中，误差也伴随在整个测量过程中。具体涉及了换能器的安装、回波信号的检测、姿态数据的融合、声速剖面的计算、不同坐标系之间的转换，所有这些过程都将对测深结果引入不同程度的误差。

2.2 多波束测深系统的误差

多波束测深的误差可以分为系统误差和随机误差，系统误差通过各种校正方法进行补偿消除；对于随机误差，其伴随整个测量过程，通过精度评估评定其大小，确定测量水深的偏差范围，进而估计水深的真值。系统误差与系统的各个单元相关，多波束系统的声学换能器阵安装误差会对水深测量结果产生影响，由于实际安装无法与设计的位置精确一致，造成实际船体坐标系与设计坐标系存在偏差，运动传感器的安装误差也会对测量结果产生影响，针对声学换能器和运动传感器安装产生的误差，在多波束系统作业时，一般会先采用参数校准的方式，测得船体坐标系在3个方向(横摇、纵摇以及艏摇)的偏差，通过实时补偿或者数据后处理，消除声学换能器和运动传感器安装带来的误差；潮位和换能器吃水误差也会导致水深误差，潮位误差与潮位测量和计算方法有关，而换能器吃水误差除了静态吃水测量误差外，还有动态吃水带来的误差，原则上，在水深大于200 m的海域进行水深测量时，不考虑潮位变化，不需要进行潮位改正[3]；声速剖面是进行声线跟踪的重要参数，其会影响波束脚印的水平位置和测点水深，严重的声速剖面误差会引起真实海底的弯曲，声速剖面误差对测深精度影响最大，通过温盐深仪或者抛弃式温深计进行实际声速剖面测量，用于声线跟踪，获得真实的波束脚印位置。这些误差是相对固定的，属于系统性误差。还有一些在实时测量中由于信号检测以及作业环境引入的随机误差，多波束测量系统通过振幅检测与相位检测两种方式对回波信号进行处理，在平坦海底的条件下，相位检测可以使得入射角计算误差达到0.05°，在近似垂直入射情况下，振幅检测可以使得射程计算误差达到约1～2个脉冲波长，该误差会随着入射角的增加而增加，这两项误差均影响水深测量中波束脚印的水平位置与水深，但总体来说对多波束测量精度影响不大[29]。

多波束测深系统的不同类型的误差有对应的处理方法。对于系统误差，通过参数校准、吃水改正、声速剖面校正等方法进行消除[30]，水深数据经过对系统误差处理改正后，理论上应该仅存在随机误差并达到较好的精度；对于随机误差，由于其无规律性，仅能通过对测深数据的精度评估评价其误差大小。而对于测量中的错误，也称为粗差，经过数据后处理过程的滤波进行消除。事实上，系统参数校正和姿态补偿并不完全，各辅助参数的测量以及上述各项改正模型也存在误差，这些误差对水深数据的影响呈现系统性，并没有彻底消除，不同种类的误差对测深数据精度的影响程度不一致，但是系统误差已经较小，而粗差也经后处理剔除。随机误差受船舶和环境噪声等外界因素影响，呈现无规律性，无法通过系统校正补偿或者数据后处理改正进行消除，是精度评估的主要对象。测深数据在经过精细处理后，已经消除了系统误差与粗差，系统的综合误差中，主要部分可以认为是随机误差，因此，综合误差近似服从高斯分布。

2.3 水深精度的评估指标

精度是对综合测量误差的估计，误差是表征测量值与真实值之间的偏差，真值是客观存在的，但无法精确测得，测量值仅能无限逼近真值，通过精度描述测量值与真值的偏离程度，从而获得真值的范围。通过对多波束测深数据的精度评估，可以描述测量水深与真实水深的偏差，评价测量数据的可信度。精度的度量指标一般采用偏差、标准差和均方根误差等评估。偏差是观测值的数学期望与真值之间的差别，反映的是观测量的精确度；标准差是表示观测值与其数学期望的差别，反映的是观测值的精密度；均方根误差是观测值与真值之间的差别，反映的是观测量的精确度。均方根误差是使用较为广泛的精度模型，它从整体意义上描述了水深测量值与真值的离散程度，其真正价值在于能提供真值可能存在的范围[31]。国际海道测量组织的误差估计要求具有95%的置信度，本文选择95%置信度的均方根误差作为精度评估指标。水深真值是一个客观存在的值，但是其又是不可知的，通常，利用多次测量的数学期望即算术平均值近似地作为真值，测量的次数越多，数学期望就越逼近真值。

多波束测深精度评估分为绝对精度评估与相对精度评估。绝对评估即采用另外一种水深测量设备进行精度评估，测深仪是一种高精度的水深测量设备，可应用测深仪衡量多波束系统的测深精度。具体方法是，在同一水域同时应用多波束声呐与测深仪进行测量，然后对两种测量设备的结果进行偏差评估，以测深仪的数据为基准，对多波束的测深结果进行精度评估，与测深仪比对进行绝对精度评估，这种方法存在一些固有缺陷，测深仪仅仅能够测得正下方的水深数据，仅能对多波束声呐的正下方数据进行比对，无法对多波束的全覆盖测量数据进行全面的评估，另一方面，测深仪与多波束声呐的测深精度处于同一量级，难以真正进行绝对精度评估。由于尚无更高量级精度的全覆盖测深设备，对多波束的测深数据需通过对其自身测量数据进行统计分析，即进行相对精度评估。相对精度评估是应用多波束系统本身的重复测深数据进行相对的精度评估，具体包含两种方式，一种是定点静态精度评估，采用船舶在定点状态下，例如开启船舶动力定位系统的情况下，对经过后处理的测深数据进行精度评估；另一种是往返或交叉测线数据的精度评估，对交叉点的重复测深数据进行统计分析。

静态精度评估是在多波束测深系统静止的条件下考核其对同一位置测量深度的误差，其本质是一种系统稳定性测试，用来评价声呐系统本身的测量精度，但其无法暴露系统的多种误差源；动态精度评估方法利用不同测线的多次测量数据进行统计分析，可以表征系统的综合误差；根据误差理论，两种精度评估方法分别从系统稳定性和自符合性方面评估系统测深精度，是检验多波束测深系统精度是否符合海道测量标准的有效方法，可有效评估测量结果[11]。本文分别采用静态精度评估和交叉测线精度评估两种方法对Kongsberg EM120型多波束声呐系统采集的测深数据进行精度评估，揭示误差的分布与量级，表征水深真值的可能存在区间。

3 Kongsberg EM120深水多波束系统测深精度评估

3.1 系统概况与数据来源

EM120多波束声呐是挪威Konsberg公司生产的全海深多波束测深系统。其工作主频为12 kHz，最大ping率为5 Hz，测深范围为20～12 000 m，最大发射扇面开角为150°，一次发射接收可以形成191个波束，波束角1°×1°，工作模式为等距作业模式或者等角模式。系统的标称精度(RMS，95%置信度)为：在0°～±45°覆盖区域内，精度为0.2%倍水深；在±60°覆盖区域内，精度为0.3%倍水深；在60°～70°与-60°～-70°覆盖区域内，精度为0.5%倍水深[32]。

本文的数据来源于中国大洋调查航次，在多波束测量作业时，工作模式为等距模式，扇面开角为120°，因此本文中数据对应的系统标称精度为0.3%倍水深(95%置信度)。在系统作业前，进行了参数校正工作，把获得的横摇偏差、纵摇偏差以及艏摇偏差引入系统的测深计算中，消除了系统安装误差，由于系统采用了秒脉冲信号同步，无需进行延时校准。在获得多波束原始数据后，采用实测的声速剖面数据，对数据进行精细后处理，剔除了粗差，获得有效的水深数据，本文进行精度评估的对象即是已经过系统安装误差改正和粗差滤波，主要包含随机误差的水深数据，其误差近似服从高斯分布。

3.2 静态精度评估方法

静态精度评估是对系统在定点作业状况下，采集的数据进行统计分析。由于海洋环境的影响，船舶无法保持绝对静止状态，本文采用2014年调查船在南海作业时，船舶在开启动力定位情况下，对船舶在定点作业时采集的数据进行分析。船舶作业时，动力定位的定位点选取为船尾部，因此，船艏并非静态，而是持续往复偏转，多波束系统的波束稳定单元为保持波束脚印与航迹垂直，会依据艏向参数进行波束偏转，在静态作业时，这样就造成中央波束脚印位置保持近似不变，而边缘波束脚印旋转(图1a)，边缘波束的测量对象在不断变化，不具备统计分析的条件，中央波束近似保持指向海底同一位置，故本文提取中央波束数据进行统计分析。

船舶保持在固定位置连续测量，对中央波束的水深测量结果进行分析统计。在误差理论中，符合同一测量条件下，对同一对象多次重复测量的误差统计条件，可以采用常规误差统计分析理论。本文选用1 h内采集的多波束数据，共发射与接收1 517ping，即采集获得1 517个中央波束数据(图1b)，采用均方根误差对该中央波束数据进行精度评估。

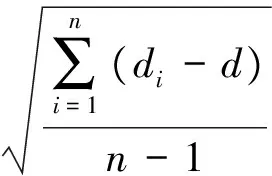
(1)

式中，σ为均方根差；di为每一ping测得的水深值；d为所有水深值的平均值即数学期望，用来指代水深真值；n为测深数据的个数。经计算，2σ=5.528 0(95%置信度)。

如果用相对误差δ来表示，则有

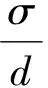
(2)

得到，δ=0.46%。

系统在中央镜像区域的标称精度为0.2%倍水深，该静态数据的样本统计结果显示，其实际探测精度低于系统标称精度。

3.3 交叉测线精度评估方法

交叉测线对海底同一区域进行不同方向的测量，对两次测量的水深数据进行统计分析，可以描述系统的自符合性，获得系统全覆盖测量的测深精度。本文选取的数据为南北向与东西向的两条交叉测线，对重叠区域的测深数据进行精度评估(图2)。

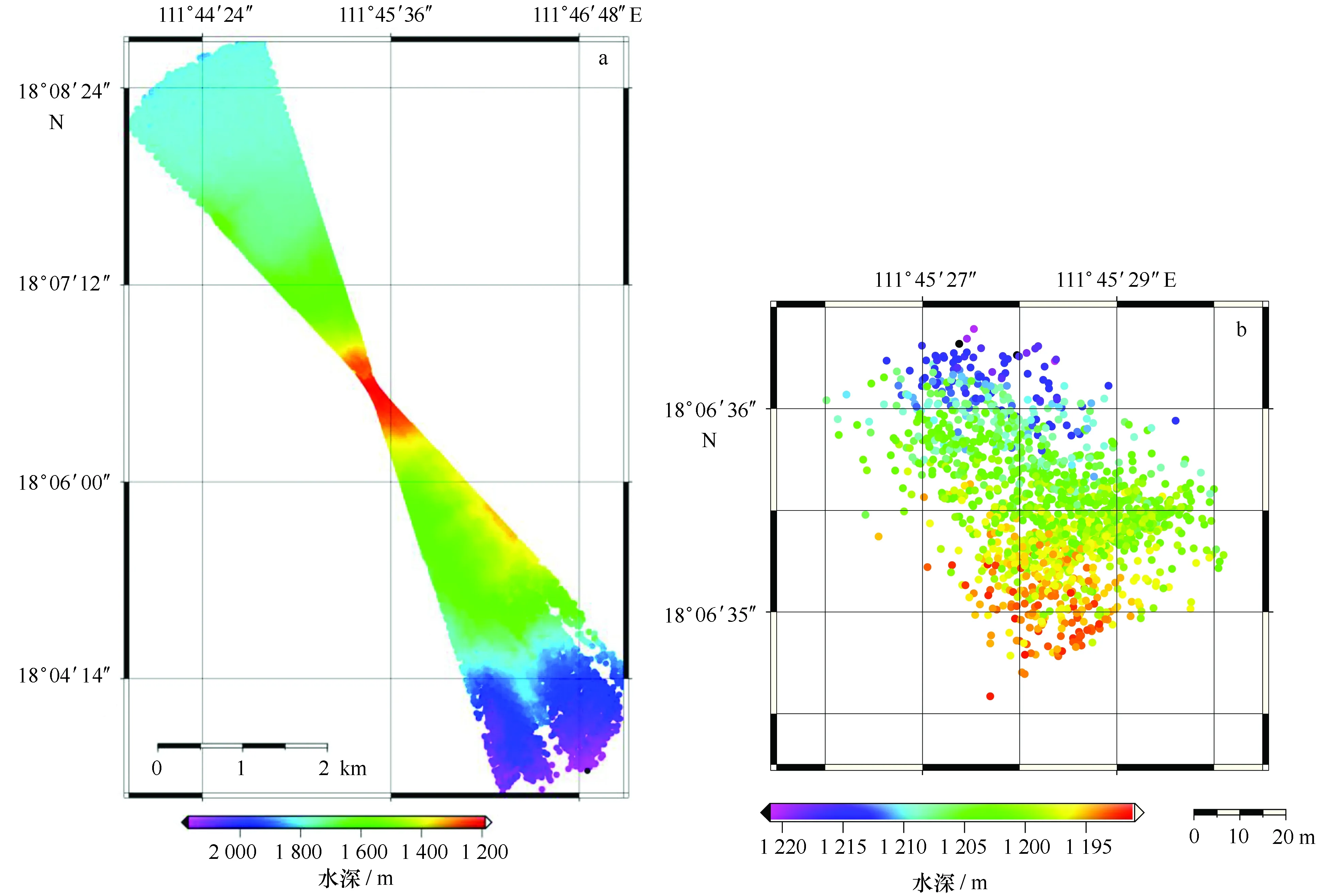
图1 1小时各个波束静态数据(a)和中央波束数据(共1 517个点)(b)Fig.1 Beam bathymetry data in one hour (a)，and central beam bathymetry data in one hour (b)

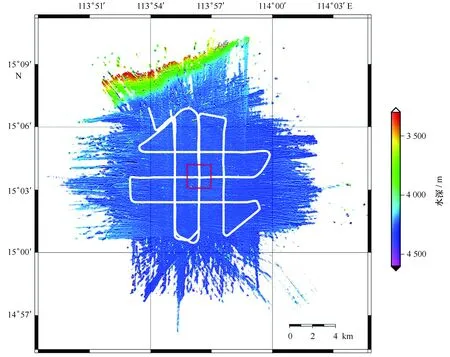
图2 交叉测线区域地形图(红框内为评估数据)Fig.2 Topographic map of the survey line (evaluation data in the red box)

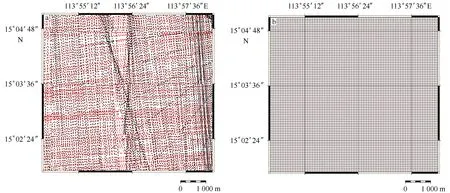
图3 选定重叠区域的水深点(a)和经过网格化处理的水深数据点(b)Fig.3 Bathymetry data of the study area(a)， and grid bathymetry data of the study area(b)

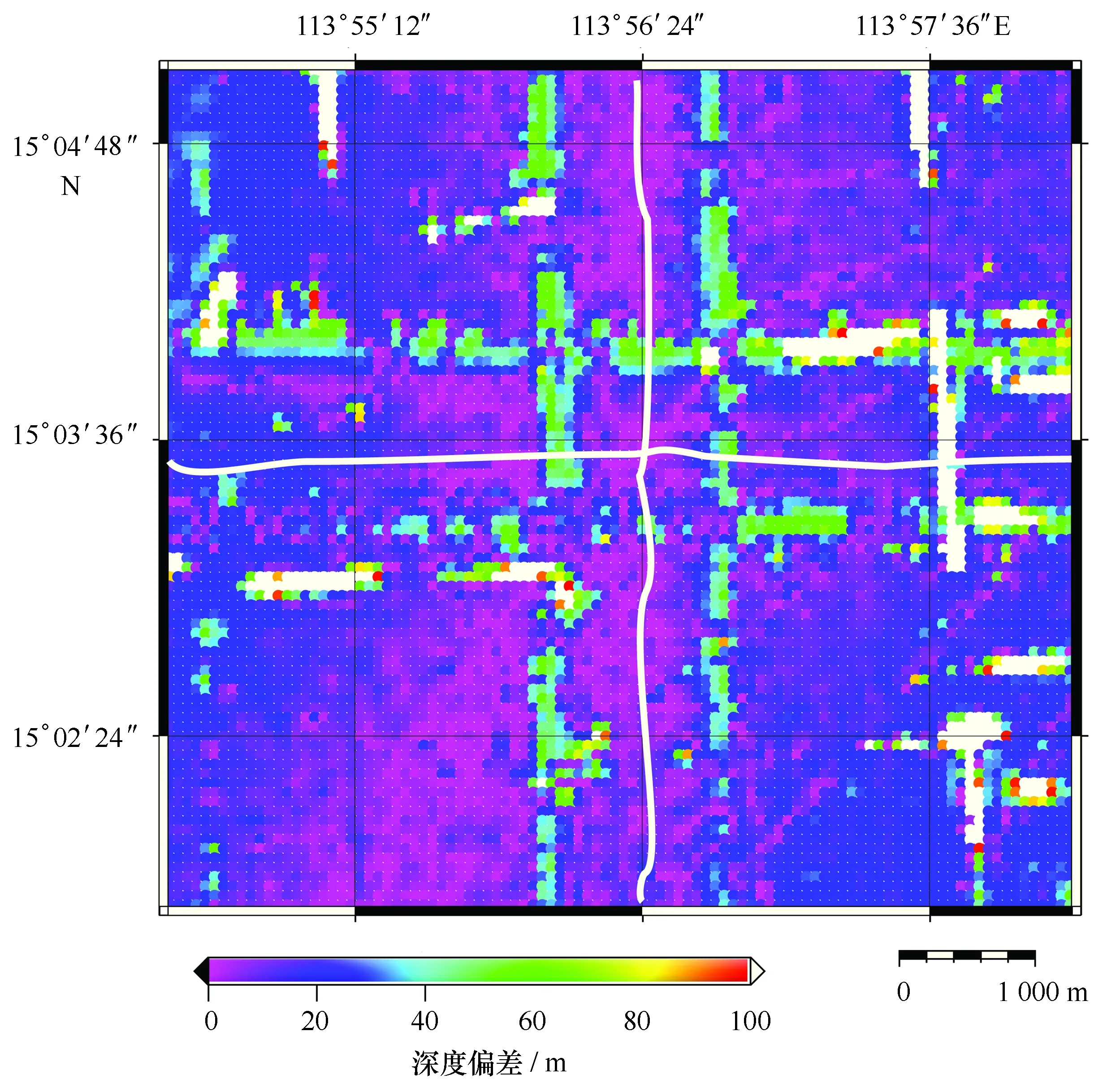
图4 往返测量重叠区域的水深数据偏差(白色线为两条交叉测线)Fig.4 Difference between the two survey line (the two cross survey lines in white colour)

测区海底较为平坦，对该区域的交叉测线数据进行精细后处理，消除了粗差。为了便于与系统指标进行对比，选取发射扇面开角-60°～60°区域数据进行统计分析，重叠区域的水深点见图3a，其中，红色点为南北向测线数据，黑色点为东西向测线数据。由于两条测线的波束脚印地理位置并不一致，为了使得数据统计分析结果可靠，对原始的水深数据进行网格化处理，获得同一地理位置的两次测量水深值。原始数据中，波束脚印之间的距离约为100 m，采用100 m网格间距对数据网格化，网格化后的数据见图3b。

利用均方根误差进行计算：

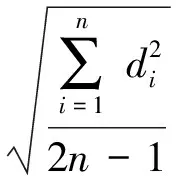
(3)

式中，σ为均方根差；di为两次测深值的偏差；n为一条测线的测深数据个数。经计算，得2σ=35.974(95%置信度)，相对误差δ=0.84%。

计算的样本精度低于系统的标称精度。为了直观表现数据误差的分布，对两条测深数据的偏差进行分析(图4)，结果表明，在中央波束两侧，数据偏差较大，边缘探测误差应该是精度降低的主要原因。该误差一直出现在探测结果中，呈现系统性，在数据后处理中，基于地形相关性认为该水深数据具有合理性，不认为其是粗差，数据后处理时无法消除。通过对交叉数据进行处理，重叠区域的水深偏差可以展现出误差分布，有助于判读误差来源。

4 结果

系统标称的精度，是系统在理想的作业工况条件下才可达到的，是系统精度指标的上限。在实际作业环境中，由于各方面的限制，测深精度一般难以达到系统的标称精度，本文的样本数据精度略低于系统标称精度。国际海道测量组织为了适应当今测深技术的发展，更加有效的描述不同测量目的的适用测深精度，对精度要求制定了国际化标准，并给出了不同测量等级对应的精度要求，即规定了不同测量等级对应要求的精度下限。

IHO S-44标准对各个测量等级的精度要求提出了一套统计指标，即各测量等级的精度容限为：

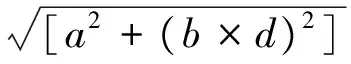
(4)

式中，a为深度常差，即所有常量误差的总和；b×d为深度相关误差，即所有深度相关误差的总和；b为深度相关误差因子；d为深度。针对本文中的测量区

域，各个等级的精度要求(95%置信度)见表1。本文中的d为交叉测线重叠区域深度数据的平均值。

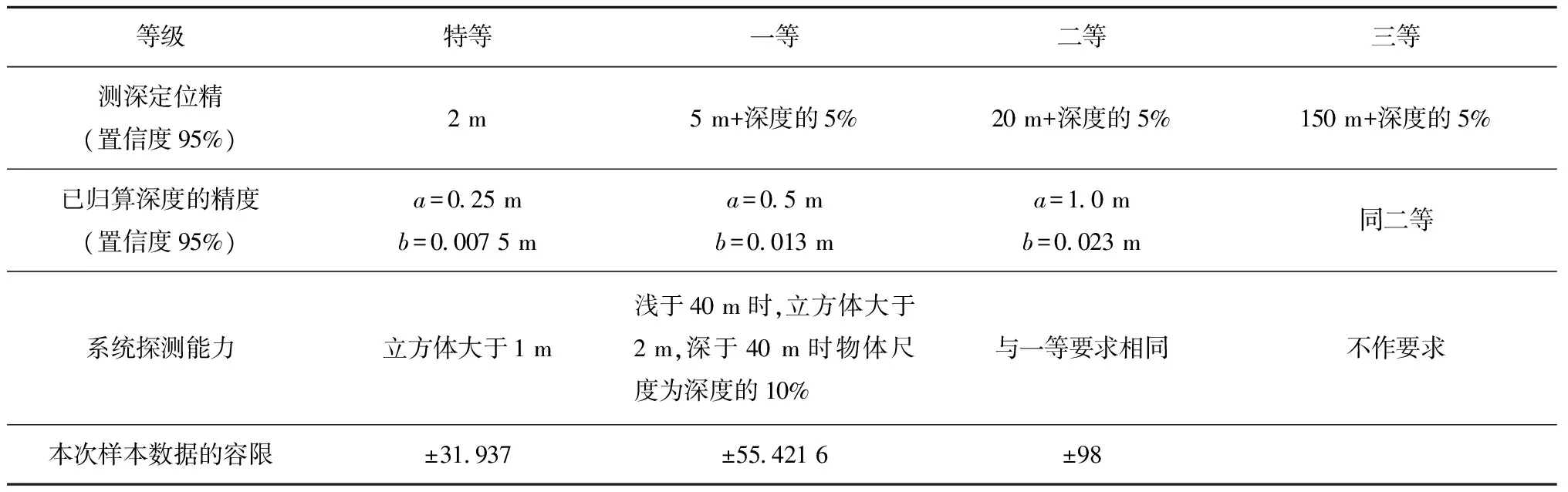
表1 IHO海道测量规范测量最低标准概要

结果表明，本文的样本数据精度优于IHO-S44要求的一等测量标准的精度容限，测量结果满足一等测量标准。

5 结语

通过系统校准，可以有效消除系统安装误差；而通过精度评估与偏差分析，能够估计随机误差的量值，并揭示随机误差分布，系统校准与精度评估都是为获得水深真值服务，互为补充。在多波束水深测量作业时，从系统参数校准和精度评估两个方面对多波束测深质量进行控制，可以保证测深的可靠性，提高数据质量。静态精度评估和交叉测线动态精度评估为多波束测深数据的误差估计提供了有效的表征方法，静态精度评估可以表征测量样本的稳定性，而针对交叉测线的测深重叠区域，基于网格化方法进行动态精度评估具有实际可操作性，其结果可以表征测量样本的自符合性。交叉测线的重叠区域的数据偏差统计分析可以具体的展现误差量值与分布特征，有利于进行针对性的测深质量控制。

[1] International Hydrographic Organization. IHO Standards for Hydrographic Surveys Special Publication N44[S]. 2008．

[2] Dix M, Abd-Elrahman A, Dewitt B, et al. Accuracy evaluation of terrestrial LiDAR and multi-beam sonar systems mounted on a survey vessel[J]. Journal of Surveying Engineering, 2011, 138(4): 203-213．

[3] 国家质量技术监督局. 中华人民共和国国家标准GB 17378.2-2007 海洋调查规范第10部分:海底地形地貌调查[S]. 2007．

The State Bureau of Quality and Technical Supervision. GB 17378.2-2007 Specification for oceanographic survey—Part 10 Submarine topography and geomorphology[S]. 2007．

[4] 国土资源部. DZ/T 0292-2016 海洋多波束水深测量技术规程[S]. 2016．

Ministry of Land and Resources of the Peoples’s Republic of China. DZ/T 0292-2016 Technical regulations for application of marine multi-beam bathymetric survey[S]. 2016.

[5] 梁志诚, 黄文骞, 魏帅, 等. 多波束测量的精度控制与规范指标[J]. 测绘工程, 2016, 25(2): 57-60．

Liang Zhicheng, Huang Wenqian, Wei Shuai, et al. Precision control and standard indexes of multi-beam surveying[J]. Engineering of Surveying and Mapping, 2016, 25(2): 57-60．

[6] 朱庆, 李德仁. 多波束测深数据的误差分析与处理[J]. 武汉测绘科技大学学报, 1998, 21(1): 1-4．

Zhu Qing, Li Deren. Error analysis and processing of multi-beam soundings[J]. Journal of Wuhan Technical University of Surveying and Mapping, 1998, 21(1): 1-4．

[7] 李家彪, 郑玉龙, 王小波, 等. 多波束测深及影响精度的主要因素[J]. 海洋测绘, 2001(1): 26-32．

Li Jiabiao, Zheng Yulong, Wang Xiaobo, et al. Multi-beam sounding and the main factors affecting the depth accuracy[J]. Hydrographic Surveying and Charting, 2001(1):26-32．

[8] 吴自银, 金翔龙, 郑玉龙, 等. 多波束测深边缘波束误差的综合校正[J]. 海洋学报, 2005, 27(4): 88-94．

Wu Ziyin, Jin Xianglong, Zheng Yulong, et al. Integrated error correction of multi-beam marginal sounding beam[J]. Haiyang Xuebao, 2005, 27(4): 88-94．

[9] 陈非凡. 多波束条带测深仪的动态测量误差评估[J]. 海洋技术, 1999, 18(1): 42-45．

Chen Feifan. Estimation of dynamic measuring error for multi-beam swath bathymeter[J]. Ocean Technology, 1999, 18(1): 42-45．

[10] 李宜龙, 殷晓冬, 张立华, 等. 交叉检查在多波束测深精度评估和误差分析中的应用[J]. 海洋技术, 2006, 25(1): 119-123．

Li Yilong, Yin Xiaodong, Zhang Lihua, et al. The application of crosscheck in multi-beam accuracy evaluation and error analysis[J]. Ocean Technology, 2006, 25(1):119-123．

[11] 吴英姿, 徐新盛, 乔力争. 多波束测深系统的精度评估方法研究[J]. 海洋技术, 2003, 22(3):65-69．

Wu Yingzi, Xu Xinsheng, Qiao Lizheng. The evaluation method of the precision of the multi-beam bathymetric system[J]. Ocean Technology, 2003, 22(3):65-69．

[12] 吴超, 殷晓冬, 张立华, 等. 基于不确定度的多波束测深数据质量评估方法[J]. 海洋测绘, 2009, 29(5):11-14．

Wu Chao, Yin Xiaodong, Zhang Lihua, et al. The method of quality estimation in multi-beam sounding data based on uncertainy[J]. Hydrographic Surveying and Charting, 2009, 29(5):11-14．

[13] 高君, 肖付民, 裴文斌, 等. 多波束测深精度检定方法[J]. 测绘科学技术学报, 2012, 29(3): 179-182．

Gao Jun, Xiao Fumin, Pei Wenbin, et al. Calibrating the depth accuracy of multi-beam sounder[J]. Journal of Geomatics Science and Technology, 2012, 29(3):179-182．

[14] 马延霞. 多波束条带测深系统测深精度评估方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2007．

Ma Yanxia. A study on surveying accuracy of estimation in multi-beam sounding system[D]. Harbin: Harbin Engineering University, 2007．

[15] 杨广义. 基于多波束测深数据的海底地形建模技术及精度评估研究[D]. 郑州：解放军信息工程大学, 2010．

Yang Guangyi. Research on benthal terrain modeling technology and precision evaluaion base on multi-beam data[D]. Zhengzhou: PLA Information Engineering University, 2010．

[16] 唐秋华, 陈义兰, 路波, 等. EM1002S与GeoSwath多波束声呐系统测深精度比较分析[J]. 海岸工程, 2013, 32(4): 56-64．

Tang Qiuhua, Chen Yilan, Lu Bo, et al. Comparison of sounding accuracy between multi-beam sonar systems EM1002S and GeoSwath[J]. Coastal Engineering, 2013, 23(4):56-64．

[17] 肖波, 盛堰, 刘胜旋. 多波束测深质量评价方法分析[J]. 海洋测绘, 2013, 33(3): 56-58．

Xiao Bo, Sheng Yan, Liu Shengxuan, et al. Method for multi-beam echosounding quality evaluation[J]. Hydrographic Surveying and Charting, 2013, 33(3):56-58．

[18] 黄辰虎, 陆秀平, 欧阳永忠, 等. 多波束水深测量误差源分析与成果质量评定[J]. 海洋测绘, 2014, 34(2): 1-6．

Huang Chenhu, Lu Xiuping, Ouyang Yongzhong, et al. Analysis of error source and quality assessment about multi-beam sounding product[J]. Hydrographic Surveying and Charting, 2014, 34(2):1-6．

[19] Maleika W. Development of a method for the estimation of multibeam echosounder measurement accuracy[J]. Przeglad Elektrotechniczny, 2012, 88(10):205-208.

[20] Ernstsen V B, Noormets R, Hebbeln D, et al. Precision of high-resolution multi-beam echo sounding coupled with high-accuracy positioning in a shallow water coastal environment[J]. Geo-Marine Letters, 2006, 26(3): 141-149．

[21] Hare R. Depth and position error budgets for mulitbeam echosounding[J]. The International Hydrographic Review, 1995, 72(2):37-69．

[22] de Moustier C. Field evaluation of sounding accuracy in deep water multi-beam swath bathymetry[C]// Oceans 94 Oceans Engineering for Today’s Technology and Tomorrow’s Preservation’ Proceedings, 2001, 3：1761-1765．

[23] Tonchia H. Evaluation of a deep water wide swath echo sounder for hydrographic surveys[C]//Oceans 94 Oceans Engineering for Today’s Technology and Tomorrow’s Preservation’ Proceedings, 1994, 3：225-230．

[24] Eeg J. On the estimation of standard deviations in multi-beam soundings[J]. The International Hydrographic Review, 1996, 73(2):39-51．

[25] Hare R, Eakins B, Amante C. Modelling bathymetric uncertainty[J]. The International Hydrographic Review, 2011,12(6):31-42．

[26] Lurton X, Augustin J. A measurement quality factor for swath bathymetry sounders[J]. IEEE Journal of Oceanic Engineering, 2010, 35(4): 852-862．

[27] Ernstsen V B, Noormets R, Hebbeln D, et al. Precision of high-resolution multi-beam echo sounding coupled with high-accuracy positioning in a shallow water coastal environment[J]. Geo-Marine Letters, 2006, 26(3): 141-149．

[28] 刘胜旋, 张瑶, 马金凤, 等. 多波束测深成果精度评估方法探讨[J]. 海洋测绘, 2016, 36(5): 36-39．

Liu Shengxuan, Zhang Yao, Ma Jinfeng, et al. Accuracy assessment of multi-beam echosounding data[J]. Hydrographic Surveying and Charting, 2016, 36(5):36-39.

[29] 李家彪. 多波束勘测原理技术与方法[M]. 北京: 海洋出版社, 1999．

Li Jiabiao. Multi-beam Sounding Principles Survey Technologies and Data Processing Methods[M]. Beijing: China Ocean Press, 1999．

[30] 刘胜旋, 关永贤. 多波束系统的参数误差判断及校正[J]. 海洋测绘, 2002, 22(1): 33-37．

Liu Shengxuan, Guan Yongxian, The determination and calibration for multi-beam system parameters[J]. Hydrographic Surveying and Charting, 2002, 22(1):33-37．

[31] 张云端, 禄丰年. 数字高程模型DEM精度研究[J]. 测绘与空间地理信息, 2007, 30(3): 120-123．

Zhang Yunduan, Lu Fengnian. Research on precision of digital elevation models[J]. Geomatics & Spatial Information Technology, 2007, 30(3):120-123．

[32] Kongsberg. EM120 multi-beam echo sounder product description[R]. Kongsberg Maritime AS, Norway, 2005.

Accuracy evaluation of multibeam echo sounder bathymetry data

Zhang Guoyin1，2， Tao Chunhui1，2， Wang Ao1，2，3， Deng Xianming1，2， He Yonghua1，2

(1.SecondInstituteofOceanography，StateOceanicAdministration，Hangzhou310012，China; 2.KeyLaboratorySubmarineGeosciences，StateOceanicAdministration，Hangzhou310012，China; 3.InstituteofGeophysicsandGeomatics，ChinaUniverstiyofGeosciences，Wuhan430074，China)

Bathymetry accuracy evaluation of multibeam echo sounder is an important aspect of water depth measurement quality control. It is an effective method using the static data accuracy evaluation and cross line coverage data accuracy evaluation to estimate the depth samples error. In the actual investigation of the water depth， there is no data of the true water depth， so it is difficult to make statistics of the depth error. The depth data collected by Kongsberg EM120 is used to analysis， the static measurement statistics is calculated using the central beam data， then a grid method is applied to make statistics using the cross line coverage depth data. In addition， the distribution of the sample data total error is showed by the cross line coverage depth deviation. In conclusion， it is an effective way to using the statistics central beam data and the cross line coverage depth data for the water depth accuracy evaluation of multibeam echo sounder．

multibeam echo sounder; accuracy evaluation; error analysis

P733.23

A

0253-4193(2017)11-0106-09

张国堙， 陶春辉， 王奡， 等. 深水多波束声呐测深数据精度评估[J]. 海洋学报， 2017， 39(11):106-114，

10.3969/j.issn.0253-4193.2017.11.010

Zhang Guoyin， Tao Chunhui， Wang Ao， et al. Accuracy evaluation of multibeam echo sounder bathymetry data[J]. Haiyang Xuebao， 2017， 39(11):106-114， doi：10.3969/j.issn.0253-4193.2017.11.010

2016-10-27；

2017-06-26。

浙江省自然科学基金项目(LQ16D060008)；国家科技支撑计划项目(2014BAB14B01)。

张国堙(1984—)，男，山西省朔州市人，工程师，从事海底声学探测技术及应用研究。E-mail：zgysir@126.com