有限断层模型在2015年9月16日智利Mw8.3级地震海啸数值模拟中的应用与评估

闪迪,王培涛,3*,任智源,原野,3,赵联大,3,范婷婷,王宗辰

(1.国家海洋环境预报中心,北京 100081;2.国家海洋局海啸预警中心,北京 100081;3.国家海洋环境预报中心 海洋灾害预报技术研究国家海洋局重点实验室,北京 100081)

有限断层模型在2015年9月16日智利Mw8.3级地震海啸数值模拟中的应用与评估

闪迪1,2,王培涛1,2,3*,任智源1,2,原野1,2,3,赵联大1,2,3,范婷婷1,2,王宗辰1,2

(1.国家海洋环境预报中心,北京 100081;2.国家海洋局海啸预警中心,北京 100081;3.国家海洋环境预报中心 海洋灾害预报技术研究国家海洋局重点实验室,北京 100081)

2015年9月16日22时54分(当地时间)智利中部近岸发生Mw8.3级地震，震源深度25 km。同时，强震的破裂区长200 km，宽100 km，随之产生了中等强度的越洋海啸。海啸影响了智利沿岸近700 km的区域，局部地区监测到近5 m的海啸波幅和超过13 m的海啸爬坡高度。太平洋区域的40多个海啸浮标及200多个近岸潮位观测站详细记录了此次海啸的越洋传播过程，为详细研究此次海啸近场及远场传播及演化规律提供了珍贵的数据。本文选择有限断层模型和自适应网格海啸数值模型建立了既可以兼顾越洋海啸的计算效率又可以实现近场海啸精细化模拟的高分辨率海啸模型。模拟对比分析了海啸的越洋传播特征，结果表明采用所建立的模型可以较好地再现远场及近场海啸特征，特别是对近场海啸的模拟结果非常理想。表明有限断层可以较好地约束近场、特别是局部区域的破裂特征，可为海啸预警提供更加精确的震源信息，结合高分辨率的海啸数值预报模式实现海啸传播特征的精细化预报。本文结合观测数据与数值模拟结果初步分析了海啸波的频散特征及其对模型结果的影响。同时对观测中典型的海啸波特征进行的简要的总结。谱分析结果表明海啸波的能量主要分布在10～50 min周期域内。这些波特征提取是现行海啸预警信息中未涉及，但又十分重要的预警参数。进一步对这些波动特征的详细研究将为海啸预警信息及预警产品的完善提供技术支撑。

有限断层；数值模拟；地震海啸；海啸浮标；自适应网格

1 引言

近10多年来重大海啸灾害呈高发态势，全球范围内平均每年均有破坏性海啸事件发生，远高于20世纪每6年一次的频率，据统计，海啸灾害已造成245 622人死亡，129 658栋房屋受损，直接经济损失超过2 500亿美元。由此可见，海啸灾害已成为世界上最严重的海洋灾害之一，严重威胁着全球沿海居民生命财产安全。为了尽可能避免或降低未来海啸事件对人类造成的灾难，沿海国家及地区政府和科研团体应尽快完善本区域的海啸预警系统与监测网络的建设，并加强本区域的海啸灾害风险评估及区划技术的研发[1-4]。

在经历了2004年印度洋大海啸、2010年智利大海啸、2011年日本东北大海啸等重大海啸事件之后，各沿海国家逐步提高了应对海啸灾害的关注度，相继建立了适合本区域的海啸预警系统，初步具备了应对越洋海啸和区域海啸的能力，但有效的应对近场海啸的能力仍存在较大不足[5]。近年来，随着实时海啸监测技术、快速震源机制解反演技术的发展，为近场海啸预警系统的完善提供了有力的技术支撑[6-9]。

准确刻画海啸源破裂过程或能量特征已成为现代海啸预警技术的核心部分[10]。目前，大部分海啸预警系统为了满足快速预警的需求，主要基于对短周期地震波的分析来获取地震参数信息和同震形变场[11]进行海啸定量预警。由于短周期地震波无法携带完整的地震能量释放信息，经常导致地震规模被低估；同样，各项同性均一滑动场模型刻画地震破裂形变场分布精度较低，对近场海啸评估结果影响较大[12]。因此对于近场海啸预警则需要更精确的海啸源支持。

目前，随着科学观测技术的提高，越来越多的海啸监测记录和地震探测数据被应用于同震位移场的重构和反演计算。利用海啸浮标数据或实时地震数据反演的有限断层解可以描述详细的地震破裂特征，这种模型称为有限断层模型(Finite Fault Solution Model)。该模型将整个断层面剖分为多个相等面积的子断层，每个子断层具有独立的局部震源机制解，并根据断层的破裂速度以及子断层的破裂时间构建随时间变化的动态破裂过程。Wei等[13]指出了基于海啸浮标反演的有限断层模型在刻画海啸传播特征方面更为准确；景惠敏等[14]利用海啸模拟结果和近场观测数据对有限断层模型的精度进行了验证；Yamazaki等[15]利用有限断层模型很好的模拟了2011年日本东北地震海啸近场传播特征及陆架共振效应；王培涛等[16]分析了有限断层模型与均一滑动场模型对海啸产生、传播、淹没特征的影响及各自的误差。综上研究对于有限断层模型在模拟海啸传播特征方面起到了推动作用。

本文基于有限断层模型和高精度有限体积水动力模型模拟分析了2015年9月16日智利Mw8.3级地震海啸越洋传播特征，评估分析了有限断层模型对本次地震海啸数值预报的影响，为今后海啸预警、海啸灾害风险评估及区划在运用有限断层模型进行数值模拟研究具有借鉴意义。

2 2015年9月16日智利Mw8.3级地震海啸事件概述

由于纳斯卡板块每年以6.5～7 cm的速度向美洲板块俯冲，导致南美洲的西海岸一直处于地震频发地带，1960年发生在智利南部的9.5级强震是有史以来记录到的最大地震，其破裂长度超过900 km，最大滑移量超过40 m[17-18]。2015年9月16日22时55分(北京时间17日6时55分)位于纳斯卡板块和南美洲板块之间的南美洲俯冲带发生8.3级地震。据美国地质调查局(USGS)，震中位置距智利科金博大区伊亚佩尔市以西46 km，震中位于31.6°S，71.7°W，震源深度25 km。Okuwaki等[19]通过动态波形反演方法分析了本次地震的破裂过程，认为破裂的最大滑移量集中在震源位置西北72 km处；Ye等[20]利用W震相分析了震源参数，地震矩的范围为3.7×1021～2.7×1021N·m，最大滑移量在7～10 m之间。本次地震引发了泛太平洋范围的海啸，远场虽未有人员伤亡的报道，但在近场本次地震海啸共造成至少15人死亡，1人失踪，14人受伤，2 305间民房损毁，10 044间民房受到不同程度的毁坏，直接经济损失高达6亿美元。

震后数分钟内，海啸袭击了智利近岸区域。地震发生40 min后，32402 DART浮标(距离震中583 km)率先记录到海啸波，高度为0.1 m，之后海啸波袭击了整个智利沿岸，其中科金博港口潮位站(COQUIMBO)监测到本次事件最大波高，高度为4.75 m。科金博市大部分地区被海水淹没，对港口、渔场以及城镇造成了严重的破坏[21]。据报道，在震源附近海啸波爬高接近10 m，疏散沿岸近一百万居民。

近5年来，智利沿岸海域发生了3次大规模的地震事件，均引发了太平洋范围的海啸，同一俯冲带内接连发生如此规模的逆冲型地震，大大提高了该区域海啸危险性及对该地区海啸灾害的关注度。2010年2月27日智利南部发生8.8级地震并引发海啸，事件共造成525人死亡，其中124人死于地震海啸[22]。事后智利政府升级海啸预警系统，提高公众对海啸灾害的认知程度和逃生技能。2014年4月1日智利伊基克发生了8.2级地震，海啸预警能力和居民防灾减灾意识的提高大大降低了地震海啸的伤亡率。由此可见，纳斯卡板块和南美洲板块频繁的相互作用，致使智利沿岸呈地震海啸频发区和重灾区。定量评估该区域海啸源对海啸数值预报的影响对于应对该区域的地震海啸具有重大现实意义。

3 精细化地震海啸数值模型的建立

海啸数值预报模型是探索海啸生成机制、评估海啸灾害和建立实时海啸预警系统的重要工具和技术手段；一个完善的海啸预警系统必须能够快速、准确的给出海啸到达近岸的时间、海啸在近岸的波幅以及海啸淹没的范围，这些信息是建立海啸撤离方案，进行海啸防灾减灾最主要的依据；而这些最基本预警信息的获得都无疑需要直接或间接的通过海啸数值预报技术来实现。地震海啸数值模型应涵盖海啸的整个物理过程的生命周期，主要包括3个阶段：海啸的产生、传播及淹没。

3.1 海啸源模型

断层模型直接关系到海啸波在大洋中的传播及海啸与近岸的相互作用，海啸源的适用性对海啸模型模拟结果显得尤为重要。目前海啸源的反演技术主要有直接通过海啸波幅信号反演和基于大地测量和地震数据数据反演的方法[23]。前者是利用直接测量的海啸波幅信号反演海平面形变场；后者是根据GPS数据和地震数据估计同震位移场。传统同震位移场是通过地震矩和震源机制方法推测同震位移场分布特征，转化成海啸产生阶段自由表面的初始边界条件。

实时地震波形数据反演的有限断层解可以快速刻画断层滑移量分布，本文引用USGS有限断层模型。该有限断层模型子断层单元长度为20 km，宽度为14 km，破裂面长度为640 km，宽度为168 km，走向角为4°，倾向19°，最大滑移量为8.04 m(表1)，利用26个远震宽频P波波形数据、11个宽频SH波波形数据和42个长周期面波波形数据进行反演计算，并与历史地震的滑移场分布进行对比，其主要能量释放集中在地震破裂的30～70 s。

表1 2015年智利地震海啸有限断层模型参数

续表1

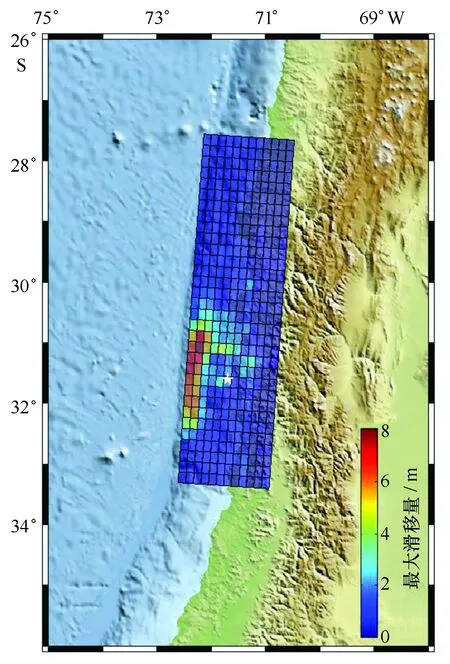
图1 USGS有限断层同震滑移量分布Fig.1 Slip distributions obtainedusing the inversions of the teleseismic by USGS

如前所述，断层模型计算的海啸初始位移场，它直接关系到海啸波在大洋中的传播及海啸与近岸的相互作用，是模拟海啸波传播的重要因素之一，根据Kajiura假设，水面变动与地震引起的瞬时断层错动的同时或数秒后发生的前提下，我们将获得的震源参数(表1)和同震位移场分布(图1)，利用Okada基于弹性错位理论的断层模型计算了海啸传播所需的初始位移场(图2)。从海啸源的形态特征我们可以看出，其形变场能量主要沿着纳斯卡板块和南美洲板块之间的俯冲带分布，呈平均具有3 m，长约200 km NNE向带状高能分布特征。另外，与均一滑动场模型计算的规则结果相比较，有限断层模型计算的海表面形变场具有更细致的局部特征。

图2 有限断层模型计算的海底位移引起的海表形变场分布Fig.2 Sea surface deformation derived from finite fault solutions model

3.2 海啸数值模型的建立

作为海啸预警、科学研究和风险评估的核心工具，海啸数值模型发展至今能够较为准确的重现海啸产生、传播和淹没的整个过程。目前国际上有许多优秀的海啸数值模式，例如基于不考虑物理频散效应的非线性浅水方程(NSWE)的COMCOT[24]、MOST[25]和Geoclaw[26]等，以及考虑频散项的Boussinesq方程或类Boussinesq方程的Funwave-TVD[27]、Neowave[28]等。

本文利用GeoClaw数学模型作为此次数值模拟的模型，该模型是由美国华盛顿大学应用数学系George D L和LeVeque R L基于波浪追逐原理和自适应网格加密技术研究开发的。该模型根据越洋海啸的传播特征，考虑了海啸波在近岸传播的非线性作用、底摩擦和科氏力效应，根据追踪波幅变化确定是否加密计算，对海啸波影响小的区域进行粗网格分辨率计算，当到达近岸时波幅增大，模型会自动加密，提高计算分辨率。其主要优点在于解决了高分辨率和计算效率之间的矛盾，提高了运行效率。

模型的控制方程为：

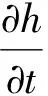
(1)

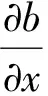
(2)

(3)

(4)

(5)

式中,g为重力加速度；h为总水深；u和v分别为x和y方向的深度平均流速；t为时间；f为科氏力系数；b为海底表面水位；τx和τy分别为x和y方向底摩擦项，其中n为曼宁系数。

相对于海啸源特征和海啸数值模式精度，影响海啸数值模型的计算精度的重要因素是水深及地形数据的分辨率[29]，研究区域内不同质量的地形水深数据，必然会导致模拟精度在一定程度上的下降。本文的模拟计算范围是65°S～65°N，115°E～65°W，基本涵盖了太平洋及其边缘海范围。考虑大洋中海啸波长的尺度为数百千米，故大洋中采用5′网格分辨率计算，可以提高计算效率，地理信息数据来自ETOPO1(https://www.ngdc.noaa.gov/mgg/global/global.html)。当海啸波传播到近岸区域后，水体波动特性因受到地形影响而改变，ETOPO系列水深分辨率在模拟港口海底高程的精细模型中还不够精确。因此，在智利近岸沿海区域补充了SRTM3数据，其分辨率为100 m左右，通过插值得到计算模型中每个网格点上的具体高程值，用来修正SRTM3数据预插值数据结果，水深数据融合GEOBCO_08数据获得。计算过程中通过自适应网格加密计算，最高网格分辨率可达30 m，根据波浪特征追踪加密判断的标准为1 cm。同时，海啸传播到近岸后，底摩擦效应远比粗网格计算时显著，模型中曼宁系数为0.025。本文选取了20个海啸浮标和14个近岸海啸监测站(图3)，利用前文有限断层海啸源作为初始条件，对智利地震海啸在远场和近场的传播特征进行了数值模拟，通过对海啸传播数值模拟结果的有效性检验，从而也实现了对本文选用的有限断层模型的评估释用，为地震参数的合理性与适用性提供了一种有效的校正方法。

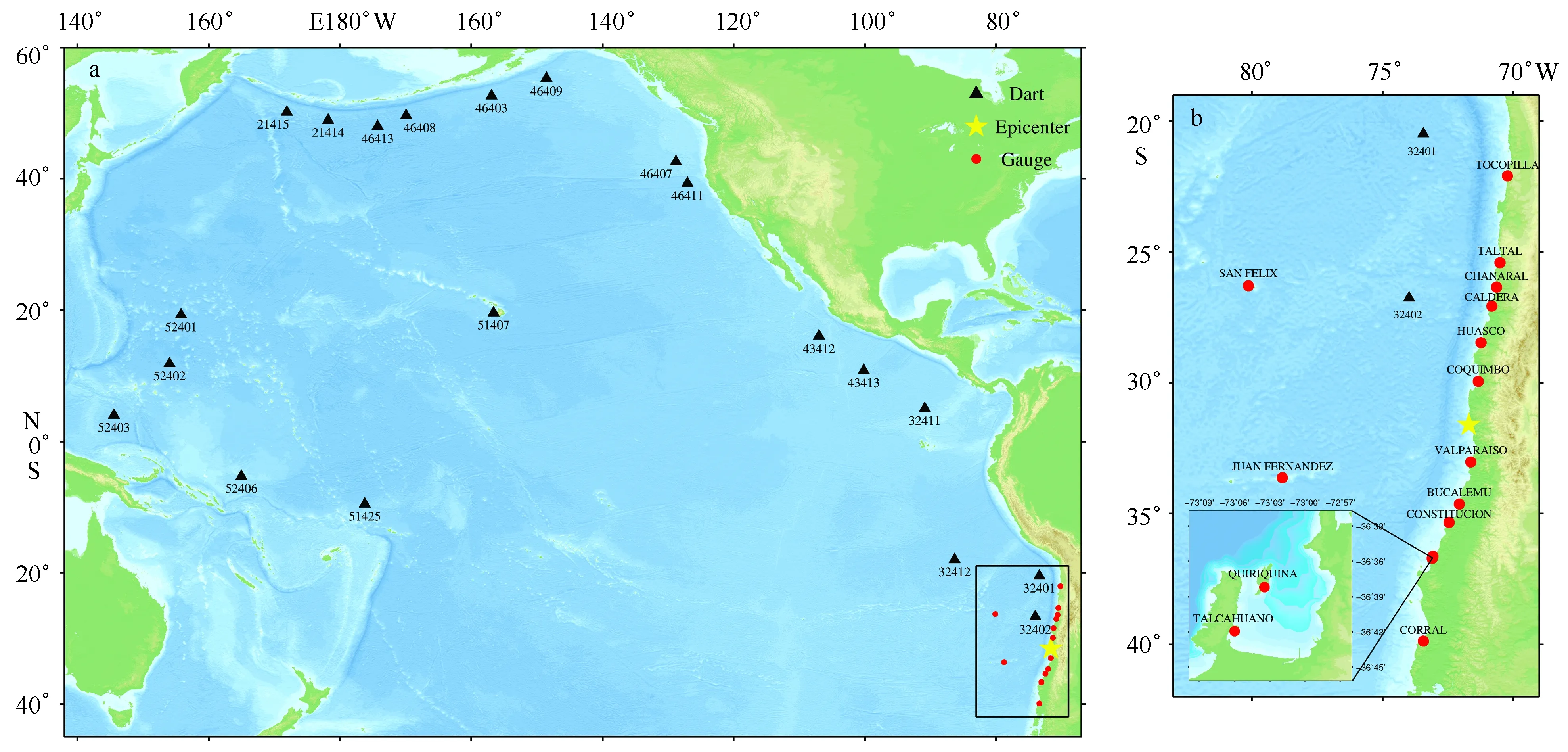
图3 深海浮标(a)及近岸监测站(b)位置示意图Fig.3 The location of DART buoys(a) and coastal tide-gauge stations(b)

4 2015年智利地震海啸数值模拟

2015年9月16日22时55分(北京时间17日6点55分)智利中部近岸(31.6°S，71.7°W)发生8.3级地震，震源深度为25 km，并引发了泛太平洋范围的海啸。除了海啸近场的智利沿岸潮位观测系统外，海啸还被布放在太平洋的数十个海啸浮标及太平洋沿岸国家数百个高分辨率、高质量的数字化海平面监测仪器所记录。这些宝贵的数据无疑是我们校正模型、检验海啸远场及近岸的传播特征的前提。

4.1 远场海啸波模拟

地震发生后引发了泛太平洋范围的海啸。海啸

浮标是海啸预警系统监测体系的重要组成部分，是目前在大洋中监测海啸最为有效的手段。通过浮标数据不仅可以准确的刻画海啸在大洋中的传播特征，还可以反演海啸源参数信息。海啸浮标提供了3种采样间隔，分别为15 s，1 min和15 min，当遇到海啸事件后，浮标由常态的15 min采样间隔转变为15 s，持续几分钟后，变为1 min并维持到事件结束。因此原始浮标数据会出现时间上不连续或重复的现象。本文选取了20个DART浮标数据用来分析深海及远场海啸波的传播特征(表2)，其中32402浮标距震源位置最近，距震源583 km，记录的最大波高接近10 cm。

表2 海啸浮标特征参数

续表2

图4 有限断层模型条件下海啸浮标波幅时间序列模拟对比Fig.4 Comparisons of observed and simulated time series based on the finite fault solution models at DART buoys

图4为数值计算得到的20个浮标站点位置的传播序列和实测数据的对比。从图4中不难发现位于近场的32402、32401、32412及32411浮标由于距离源较近，且周边没有局地变化强烈的地形干扰，海啸信号表现出了典型的海啸瞬态脉冲的波形，海啸的首波即为最大波幅。海啸波特征主要受控于海啸源参数特征。数值模拟海啸波到时及最大波幅与观测吻合良好。在接近震源长轴方向上的43412、43413、46411及46407海啸浮标除43412外，海啸波首波波幅即为最大海啸波幅特征，考虑43412可能有反射波影响，最大波幅出现在首波后的50 min后。相比近场的浮标站而言，后相波开始出现较大波幅的振荡现象。尽管如此，数值模拟对首波的模拟还是较为理性的。由于模型所采用的地形资料与实际间的误差，出现了最大8 min的位相误差，但相对于海啸传播时间而言这个误差可以忽略。与前类似，在稍偏离长轴方向的46409、46408、46413和46403浮标信号主要受长波及陆地边界反射影响影响，出现波幅较大的振荡特征，但海啸波能量基本出现在首波。模拟的首波波幅有些低估。位相频移程度随着传播距离的增加没有显著变化，进一步说明在该方向上的短波成分并不占优。在与断层走向垂直的方向上即海啸能量的主传播方向，也就是震源短轴方向海啸频移现象随着传播距离的增加而加强，考虑在该方向上的海啸波主要是震源短轴的短波产生的频散效应。受传播路径上岛链、海底山脉等地形特征的折射与散射影响，海啸波幅最大能量均未出现在海啸首波位置，而是在首波后的数个周期内。如前所述，这种延迟要比海啸的越洋传播时间小两个量级，可以忽略。将频移进行人为的订正后，得到在能量主传播方向上首波波幅的模拟结果较为理想。

综合海啸能量传播的各条路径上的观测数据不难看出该海啸在深海传播过程中，首先到达的是海啸的减水过程，这是该次海啸的一个主要特征，遗憾的是我们的模型没有捕捉到这细微的波结构特征。考虑可能的原因是海啸源的边缘处应该存在显著的水位下降区域。同时，模型对首波后的短波成分的刻画并不理想，考虑主要由于用于计算传播过程的地形精度不够高、物理模型中没有考虑物理的频散效应和海底形变与海面位移的转换机制并不清楚等因素所致。

由于数值模拟过程中没有考虑到海啸波的频散、海水的压缩性和海啸波的弹性变化，导致观测数据与模拟结果相比延迟3～20 min。为此本文根据这一典型现象，研究了首波延迟时间与海啸传播距离即浮标位置距离震源远近。图5可以定性的给出首波延迟与海啸传播距离的线性正相关关系，但是在某些方向上，特别是与断层走向垂直的方向上海啸的延迟会更显著。

图5 海啸波延时与距离震源关系Fig.5 The arrival time delays of the observed waveforms relative to the simulated ones versus the distances from the source

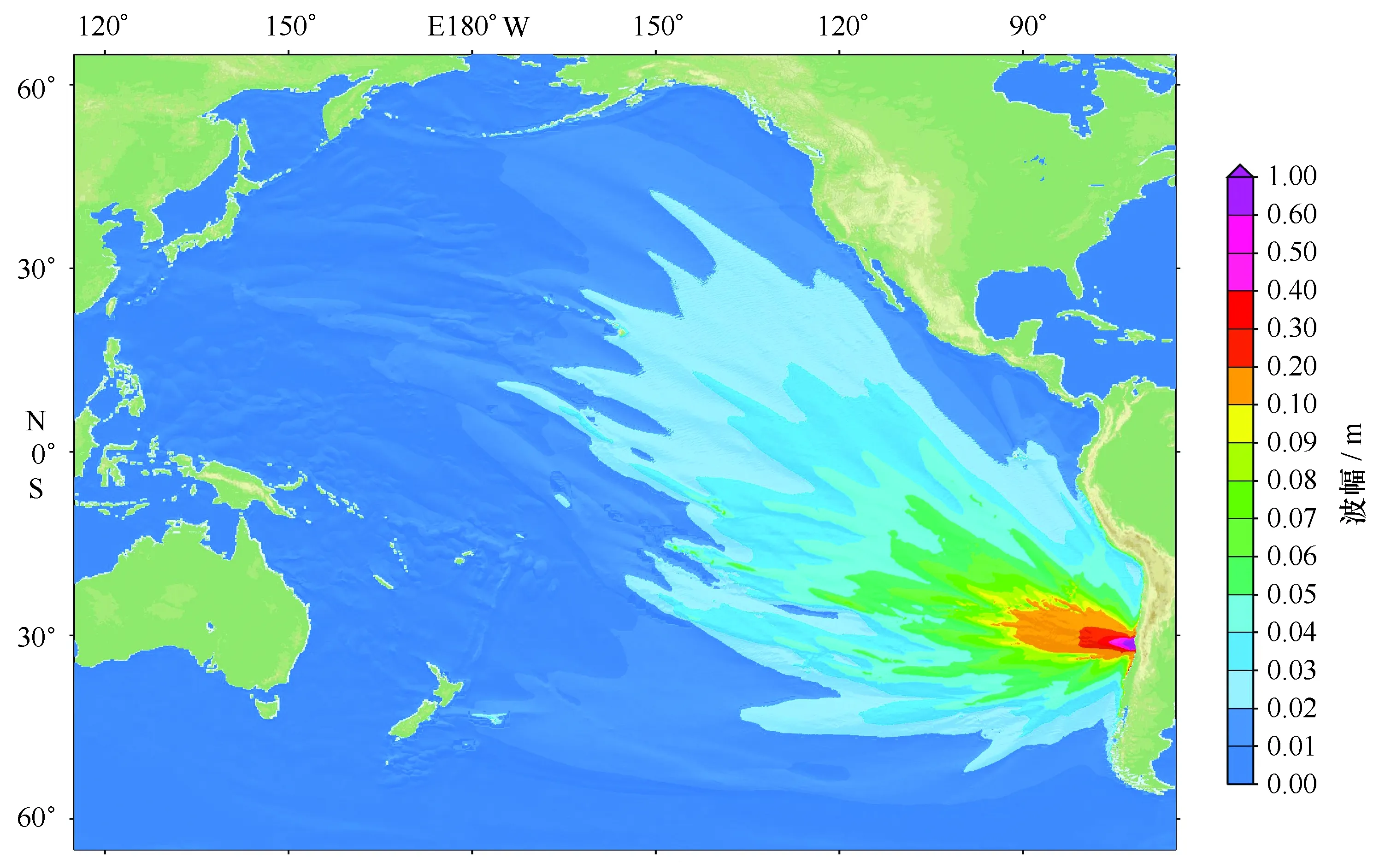
图6 有限断层模型模拟的最大海啸波幅分布Fig.6 Maximum tsunami wave amplitude obtained using the finite fault model

图7 有限断层模型条件下近岸监测站海啸波幅时间序列模拟对比Fig.7 Comparisons of observed and simulated time series based on the finite fault solution models at coastal tide-gauge stations

图8 近岸监测站海啸波观测数据小波分析Fig.8 Wacelet analysis for the coastal tide-gauge stations records

从海啸最大波幅分布(图6)来看，本次海啸波的主要能量传播方向为西北方向，另外北西北和南西南两个方向为海啸波能的次传播方向。这种海啸能量分布特征主要受断层走向的影响，其次远场海啸能量的走向还与特定的地形有关。例如当海岭的走向与海啸波传播的方向相近时，洋中脊和环绕大陆的陆架区对海啸波的传播方向具有导向作用，除了可以将波动导向更远的地方外，还可以捕捉海啸能量，使得这些地区的海啸维持长时间的振荡[30]。由此可见，海底地形决定了海啸波在大洋中的波能量流方向，其主要的能量流聚集在主要的海岭处，并以带状分布。

4.2 近场海啸波观测与模拟

强震发生半个小时后，观测资料显示智利北部港口科金博，海啸波高达4.75 m，科金博港是本次地震海啸事件受影响最重的地方之一。随后4 h内，海啸波袭击了智利沿岸700 km范围的沿岸地区。数个沿岸的港湾地区出现了较严重的淹没现象，最大海啸爬坡高度超过13 m，海啸上水距离近800 m。与深水远场不同的是在近场近岸观测数据中(图7)，并没有发现先导波到达的负增水现象。观测数据表明，当海啸先导波到达后，在很长时间范围内海啸波在持续震荡，并且震荡过程中海啸波幅往往大于先导波。这种现象并非是海啸源初始特征所决定的，这主要是由于受到波波相互作用及局地地形和近岸特征所影响。

地震发生半小时后，海啸波抵达近岸，除了受海啸源分布特征影响外，地形与海啸的相互作用也是影响海啸传播的原因之一[30-31]。图7是数值计算得到的时间序列与潮位站实测数据的对比图。从对比结果可以看出模式计算得到的海啸先导波的相位和波幅与实际数据相吻合，此外模型基本可以准确刻画近场海啸波第一个波序列中的前3～5个波形。说明了有限断层模型在刻画近场海啸波特征方面是可信的，特别是震源短轴控制的海啸波特征模拟方面较传统的震源机制解有较明显的改善。尽管如此，对比大多数潮位站的记录和模拟结果发现，虽然首波和最大波幅模拟较为理想，但不够精确的近岸地形资料，可能导致尾波的拟合都不是很理想。由于近岸特定地形作用下长期振荡的存在，对海啸预警工作而言，除了针对首波到时、首波波幅外，也不能忽略最大波特征及尾波的存在，因此更加精确的地形、考虑更全面物理过程的海啸数值模型对海啸模拟尤为重要。

本文对近岸监测站海啸波观测数据进行了小波分析，从分析结果(图8)来看，大部分站点的小波波能主要分布在10～50 min周期域内。相比于远场，近岸海啸波主频波谱分布更广，除受复杂地形影响外，还在于海啸源特征的复杂性。如VALPARAISO，BUCALEMU，COQUIMBO，HUASCO监测点，距震源位置较近，海啸波受源的影响较大，波能量分布广泛。距震源较远的CALDERA、CHANARAL监测点记录到的波能量较为固定。分析TALCAHUANO、QUIRIQUINA、CORRAL站点表明，海啸波除包含本次事件的主要波能外，波能还集中在100～130 min周期域内，可能原因是受特殊地形影响海啸波激发了陆架固有周期的震荡[32]，而后相互作用所致。

5 结论

海底强震发生后，各机构或研究团体会陆续发布各种的描述与表征地震断层破裂特征的模型。在这些模型中，选择恰当的震源破裂模型，一直都是海啸数值预报技术研究的关键问题。本文通过选择能够刻画地震破裂局部特征的有限断层模型模拟分析了2016年智利Mw8.3级地震海啸在近场、远场的传播特征。避免了采用传统点源震源机制解估算海啸源尺度所带来的海啸强度的不确定性误差。将有限断层破裂模型与高精度、高分辨率自适应加密技术的海啸数值预报模型相结合，实现了远场大洋的高效及近岸区域的高分辨率快速计算。对比结果表明，本文采用的计算与组合策略可以较好的刻画海啸的越洋传播，特别对近岸海啸的波特给出了非常合理的刻画。

通过对远场观测数据的模拟对比分析，进一步验证了海啸波在大洋中的频散特性。这种频散特征会随着海啸传播时间而增强。同时也分析了数值模拟结果频移特征是与海啸的频散有关的，这种特征与海啸传播的方向有紧密的联系。此外，在该例中一个显著的负增水波谷首先到达现象在远场的多个观测站中出现，同样的现象在近场近岸站点没有发生，而在有些近岸站点最大波幅有延迟到达的现象，针对这些现象可能的原因有待于进一步的研究。

[1] Synolakis C E, Okal E, Bernard E N. The megatsunami of December 26, 2004[J]. Bridge, 2005, 35: 26-35.

[2] Geist E L, Titov V V, Synolakis C E. Tsunami:Wave of change[J]. Scientific American, 2006, 294(1): 56-65.

[3] Titov V V. Tsunami Forecasting, in the Sea[M]. Cambridge: Harvard University Press, 2009: 371-400.

[4] Tang L J, Titov V V, Chamberlin C D. Development, testing, and applications of site-sepcific tsunami inundation models for real-time forecasting[J]. Journal of Geophysical Research, 2009, 114(C12): 43-47.

[5] 王培涛, 于福江, 赵联大, 等. 2011年3月11日日本地震海啸越洋传播及对中国影响的数值分析[J]. 地球物理学报, 2012, 55(9): 3088-3096.

Wang Peitao, Yu Fujiang, Zhao Lianda, et al. Numerical analysis of tsunami propagating generated by the JapanMw9.0 earthquake on May. 11 in 2011 and its impact on China coasts[J]. Chinese Journal of Geophysics, 2012, 55(9): 3088-3096.

[6] Baba T, Hirata K, Kaneda Y. Tsunami magnitude determined from ocean bottom pressure gauge data around Japan[J]. Geophysical Research Letters, 2004, 31(8): 239-261.

[7] Takayama H. Statistical relationship between tsunami maximum amplitudes of offshore and coastal stations[J]. Papers in Meteorology Geophysics, 2008, 59: 83-95.

[8] Tang L J, Titov V V, Bernard E N, et al. Direct energy estimation of the 2011 japan tsunami using deep-ocean pressure measurements[J]. Journal of Geophysical Research Atmospheres, 2012, 117(C8): 72-82.

[9] Wang D L, Becker N C, Walsh D, et al. Real-time forecasting of the April 11,2012 Sumatra tsunami[J]. Geophysical Research Letters, 2012, 39(L19601): 1-6.

[10] Wei Y, Titov V V, Newman A V, et al. Near-field hazard assessment of March 11, 2011 Japan Tsunami sources inferred from different methods[J]. Oceans, 2011, 8(5): 1-9.

[11] Tsushima H, Kenji H, Hayashi Y, et al. Near-field tsunami forecasting using offshore tsunami data from the 2011 off the Pacific coast of Tohoku Earthquake[J]. Earth Planets Space, 2012, 63: 821-826.

[12] Ergin U. Comparison of the seafloor displacement from uniform and non-uniform slip model on tsunami simulation of the 2011 Tohoku-Oki earthquake[J]. Journal of Asian Earth Sciences, 2013, 62: 568-585.

[13] Wei Y, Newman A V, Hayes G P, et al. Tsunami forecast by joint inversion of real-time tsunami waveforms and seismic or GPS Data: application to the Tohoku 2011 tsunami[J]. Pure and Applied Geophysics, 2014, 171(12): 3281-3305.

[14] 景惠敏, 张怀, 吴忠良, 等. 利用海啸数值模拟结果进行海底地震有限断层模型验证[J]. 地震, 2013, 33(4): 207-213.

Jin Huimin, Zhang Huai, Wu Zhongliang, et al. Tsunami constraints on finite fault models:the March 11, 2011 Tohoku earthquake[J]. Earthquake, 2013, 33(4):207-213.

[15] Yamazaki Y, Cheung K F, Lay T. Modeling of the 2011 Tohoku near-field tsunami from finite-fault inversion of seismic waves[J]. Bulletin of the Seismological Society of America, 2013, 103(2B): 1444-1455.

[16] 王培涛, 于福江, 原野, 等. 海底地震有限断层破裂模型对近场海啸数值预报的影响[J]. 地球物理学报, 2016, 59(3): 1030-1045.

Wang Peitao, Yu Fujiang, Yuan Ye, et al. Research on the effects of the finite fault rupture models of submarine earthquakes for numerical forecasting of near-field tsunami[J]. Chinese Journal of Geophysics, 2016, 59(3): 1030-1045.

[17] Moreno M, Rosenau M, Oncken O. 2010 Maule earthquake slip correlates with pre-seismic locking of Andean subduction zone[J]. Nature, 2010, 467(7312): 198-202.

[18] Barrientos S E, Ward S N. The 1960 Chile earthquake: inversion for slip distribution from surface deformation[J]. Geophysical Journal International, 1990, 103(3): 589-598.

[19] Ryo Okuwaki, Yuji Yagi, Aránguiz R, et al. Rupture process during the 2015 Illapel, Chile Earthquake zigzag-along-dip rupture[J]. Pure and Applied Geophysics, 2016, 173(4): 1011-1020.

[20] Ye Lingling, Lay T, Kanamori H, et al. Rapidly estimated seismic source parameters for the 16 September 2015 Illapel, ChileMw8.3 Earthquake[J]. Pure and Applied Geophysics, 2016, 173(2): 321-332.

[21] Bonnefoy P, Romero S. In Chile, earthquake forces one million to evacuate[N]. The New York Times, 2015-09-17.

[22] Fritz H M, Petroff C M., Catalán P A. The Chile tsunami of 27 February 2010: Field survey and modeling[J]. Pure and Applied Geophys, 2014, 168(11): 1989-2010.

[23] 王培涛, 于福江, 范婷婷, 等. 海啸波传播的线性和非线性特征及近海陆架效应影响的数值研究[J]. 海洋学报, 2014, 36(5): 18-29.

Wang Peitao, Yu Fujiang, Fan Tingting, et al. Numerical study on the linear/nonlinear characteristics and the impacts of continental shelf effects of the tsunami waves propagating[J]. Haiyang Xuebao, 2014, 36(5): 18-29.

[24] Wang X M, Liu L F. An explicit finite difference model for simulating weakly nonlinear and weakly dispersive waves over slowly varying water depth[J]. Coastal Engineering, 2011, 58(2): 173-183.

[25] Titov V V, González F I. Implementation and Testing of the Method of Splitting Tsunami(MOST) Model[M]. Seattle: Pacific Marine environmental Laboratory Press, 1997: 1-11.

[26] George D L, LeVeque R J. Finite volume methods and adaptive refinement for global tsunami propagation and local inundation[J]. Science of Tsunami Hazards, 2006, 24(5): 2255-2263.

[27] Shi F Y, Kirby J T, Tehranirad B. Tsunami benchmark results for spherical coordinate version of FUNWAVE-TVD (Version 1.1)[R]. Newark: Center for Applied Coastal Research, University of Delaware, 2012.

[28] Yamazaki Y, Cheung K F, Kowalik Z. Depth-integrated non-hydrostatic model with grid nesting for tsunami generation,propagation, and run-up[J]. International Jourmal for Numerical Methods in Fluids, 2011, 67(12): 2081-2107.

[29] Macinnes B T, Gusman A R, Leveque R J, et al. Comparison of earthquake source models for the 2011 Tohoku-oki event using tsunami simulations and near field observations[J]. Bulletin of the Seismological Society of America, 2013, 103(2B): 1256-1274.

[30] Titov V, Rabinovich A B, Mofjeld H O, et al. The global reach of the 26 December 2004 Sumatra tsunami[J]. Science, 2005, 309(5743): 2045-2048.

[31] Zheng Jinhai, Xiong Mengjie, Wang Gang. Trapping mechanism of submerged ridge on trans-oceanic tsunami propagtion[J]. China Ocean Engineering, 2016, 30(2): 271-282.

[32] Yamazaki Y, Cheung K F. Shelf resonance and impact of near-field generated by 2010 Chile earthquake[J]. Geophysical Research Letters, 2011, 38(12): 564-570.

Application and evaluation of the 16 September 2015 Illapel, Chile Mw8.3 earthquake finite fault rupture model from numerical simulation

Shan Di1,2, Wang Peitao1,2,3, Ren Zhiyuan1,2, Yuan Ye1,2,3, Zhao Lianda1,2,3, Fan Tingting1,2, Wang Zongchen1,2

(1.NationalMarineEnvironmentalForecastingCenter,Beijing100081,China；2.TsunamiWarningCenter,StateOceanicAdministration,Beijing100081,China；3.KeyLaboratoryofResearchonMarineHazardsForecasting,NationalMarineEnvironmentalForecastingCenter,StateOceanicAdministration,Beijing100081,China)

On September 16, 2015, at 19:54 (local time) a magnitudeMw8.3 earthquake took place off the coast of central Chile, focal depth of 25 km. Meanwhile, the earthquake with rupture zone 200 km long and 100 km wide triggered moderate intensity teletsunami. The tsunami impacted approximately 700 km of the coast of Chile, some areas tsunami reached amplitudes near 5 m and tsunami run-up exceeded 13 m. Tsunami waves were subsequently recorded by more than 40 Deep-ocean Assessment and Reporting of Tsunami (DART) buoys in the Pacific Ocean and more than 200 tide gauges throughout the Pacific Ocean, a rich supply of data which study the tsunami propagation scenarios in near-filed and deep-water. This paper used the finite fault models and adaptive refinement algorithms to build a well computational efficiency and high resolution numerical tsunami model. We analyzed the teletsunami propagation characteristics. The results show that by using the established model can well reproduce the far-field and near-field tsunami process, especially on the near-field the simulation results fit well with the observational data. It indicates that the finite fault model can better depict the near-field, especially the rupture characteristics and provide more accurate source information. The fine prediction of tsunami propagation characteristics can be achieved by the finite fault model and high resolution numerical tsunami model. In this paper, using the observation data and simulation results, analyzed the frequency dispersion of the tsunami wave and its influence on the model. Meanwhile, carried out a brief summary of the typical characteristics of the tsunami wave. The wavelet analysis show that the tsunami energy is concentrated in the period band of around 10-50 min. These wave characteristics are not involved in the current tsunami warning information, but they are very important parameters. Further research on these characteristics will provide technical support for the improvement of tsunami warning information and warning products.

finite fault; numerical simulation; earthquake tsunami; tsunami buoys; adaptive refinement algorithms

P731.25

A

0253-4193(2017)11-0049-12

闪迪, 王培涛, 任智源, 等. 有限断层模型在2015年9月16日智利Mw8.3级地震海啸数值模拟中的应用与评估[J]. 海洋学报, 2017, 39(11):49-60,

10.3969/j.issn.0253-4193.2017.11.005

Shan Di, Wang Peitao, Ren Zhiyuan, et al. Application and evaluation of the 16 September 2015 Illapel, ChileMw8.3 earthquake finite fault rupture model from numerical simulation[J]. Haiyang Xuebao, 2017, 39(11):49-60, doi:10.3969/j.issn.0253-4193.2017.11.005

2016-08-04；

2017-05-04。

海洋公益性行业科研专项项目(201405026，201205034，201305031)。

闪迪(1987—)，男，北京市人，助理工程师，主要从事海洋灾害预警技术研究。E-mail:shandi@nmefc.gov.cn

*通信作者：王培涛(1981—)，男，副研究员，研究方向为海洋灾害预警技术及河口与海岸动力学。E-mail:wpt@nmefc.gov.cn