港湾共振研究综述
王岗,高俊亮,王培涛,郑金海*,董国海
(1.河海大学 海岸灾害及防护教育部重点实验室,江苏 南京 210098;2.江苏科技大学 船舶与海洋工程学院, 江苏 镇江 212003;3.国家海洋环境预报中心,北京 100081;4.河海大学 港口海岸与近海工程学院,江苏 南京 210098;5.大连理工大学 海岸和近海工程国家重点实验室, 辽宁 大连 116023)
港湾共振研究综述
王岗1,4,高俊亮2,王培涛3,郑金海1,4*,董国海5
(1.河海大学 海岸灾害及防护教育部重点实验室,江苏 南京 210098;2.江苏科技大学 船舶与海洋工程学院, 江苏 镇江 212003;3.国家海洋环境预报中心,北京 100081;4.河海大学 港口海岸与近海工程学院,江苏 南京 210098;5.大连理工大学 海岸和近海工程国家重点实验室, 辽宁 大连 116023)
港湾共振是指当外海长周期入射波浪与港湾固有周期接近时出现的大幅波动现象,它对当地的水体动力过程、船舶运动及水灾害防护与评估具有重要意义。本文分别从其共振机理、激发因素及模拟方法上回顾了国内外的主要研究成果。特别针对我国的港湾共振情况,详细介绍了典型港湾共振事件的发生特点及其产生机理。最后结合我国海岸特征及现有研究进展提出相应的研究展望,以使其得到进一步的发展和完善。
港湾共振;湖震;水波共振;波浪理论
1 引言
共振是指系统在特定周期作用下、相比其他周期以更大幅度运动的情形,而这些特定周期称之为共振周期。该现象在声学中也称之为“共鸣”,指的是物体因共振而发声的现象,如两个频率相同的音叉靠近,其中一个振动发声时,另一个也会发声。在电学中,振荡电路的共振现象称为“谐振”。港湾共振与之相似,指的是当半封闭港湾受到外力的作用,并且外力作用的周期和港湾的本征周期(也称共振周期)一致时,港湾中的水体就会发生剧烈的振荡现象,即称之为港湾共振(Harbor resonance/Harbor oscillations/Seiches)。港湾的共振周期与共振模态是港湾固有属性,由其几何形状和地形决定,通常在数分钟至数小时之间。
港湾共振可使停靠在码头和泊位的舰船产生大幅晃动,影响港口的正常装卸作业,甚至导致系船绳索断裂,致使舰船之间碰撞及船和码头建筑物碰撞,严重时还会导致舰船事故。周期较长的港湾共振会在口门处形成相当强的水流,威胁出入港口舰船的通航安全,甚至可能导致船翻人亡的灾难性事故。港湾共振还会使港底泥土流失或堆积,造成港底地势变异,久而久之,水工建筑物的根基也会被冲毁。此外,港湾共振可在短时间内引起港内水位的骤然升降,导致码头或低凹地区被淹,威胁着沿海居民的安全。如1979年3月31日日本五岛列岛的玉之浦因水位突然升高致使3名年迈的妇女溺亡[1]。
由于港湾共振所带来的巨大危害,从20世纪初就有学者开始对其展开了研究。Wilson[2]和Miles[3]曾在20世纪70年代总结了这一研究领域的进展情况;Rabinovich[4]总结了截至2009年这一领域所取得的成就。本文将从与之不同的角度阐述港湾共振的产生机制、诱发因素及其危害,在尽量避免与以上综述雷同的基础上,呈现这一领域的最新进展,特别是随着全球气候变化导致的极端海洋灾害频发,越来越多的学者投入至这一领域所取得丰硕成果。本文将分别从其产生机理、理论方法、激发因素与模拟方法上分别综述这一领域所取得的研究成果,特别总结了我国港湾共振事件的研究进展,在此基础上提出了本领域的展望。
2 共振机理
港湾共振的研究始于流体驻波的研究。早在1828年,VonderMühll[5]给出了基于长波理论常水深矩形内的驻波解。如图1所示,波浪从矩形的一边垂直传出,传至另一边后被边界反射回来又传回至起始位置,形成一个所谓的“回路”。此“回路”的长度与波长达到一定关系,便形成所谓的共振现象。类似的现象同样出现在圆形水域内,任意通过圆心的波浪路径都形成类似的“回路”。利用这一性质,郑金海等[6]和张弛等[7]分别给出了正五边形和正六边形水域内水波共振周期与水深及几何尺寸间的关系。实际上,利用该关系可以给出任意形状水域内水波共振周期。王岗等[8]通过坐标变换将线性长波方程转换为基于椭圆坐标系的水波运动方程,并采用分离变量法分别得到马丢方程描述的极角方向运动方程和拓展型马丢方程描述的径向运动方程,推导出椭圆形水域内波浪共振的解析解。该研究在长短半轴相等的情况下又可以退化为圆形水域内的水波共振问题。以上封闭水域内波浪共振和与外海联通港湾有着本质区别,它们更适合描述在内陆湖泊中的共振现象(有的文献称之为湖震,英文为seiches)。李裕澈等[9]认为1597年10月6日在我国东部地区出现的广泛湖震与珲春-汪清深地震有关。据报道,2008年汶川地震期间在东南亚的湖泊中出现剧烈水体运动现象,作者认为该次地震必然引起过国内某些湖泊出现类似的现象,只是缺乏详实观测资料佐证而已。
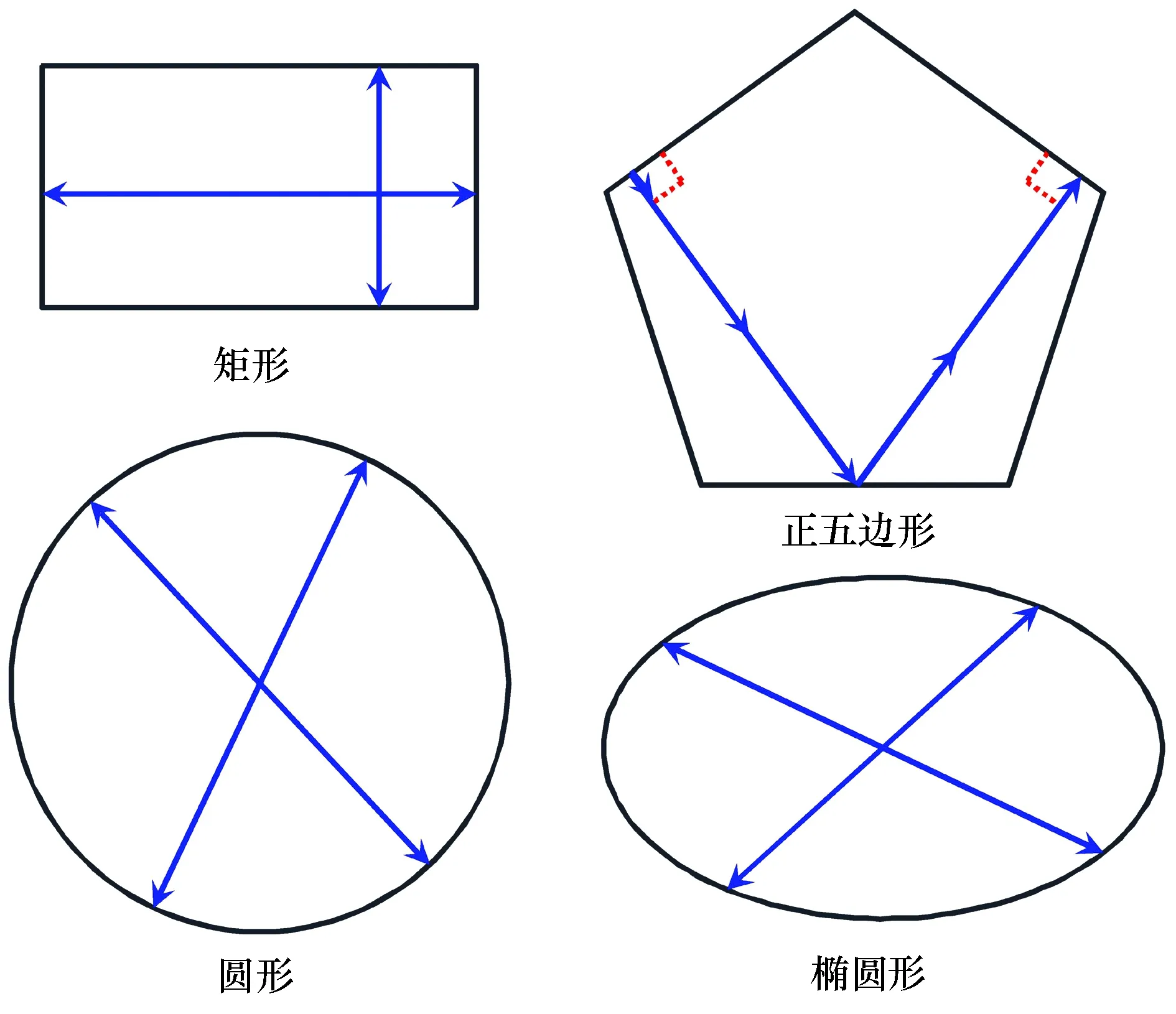
图1 矩形、正五边形、圆形及椭圆形内波浪传播示意图Fig.1 Wave propagation within rectangular, regular pentagon,circle and ellipse
港湾共振通常发生于形状较为规则,口门较窄、封闭性较好的港湾,这是由于长周期波浪具有较强的穿透性,可以绕过掩护结构作用于港湾内。如图2所示,外海传至某一狭长矩形港湾时,经过港内边壁反射的波浪在经过港湾口门处,由于水域突然变阔,部分波浪又被反射回来,使得部分波浪能量被限制在港湾内。此外,在港湾口门处,还存在着辐射波向外海散射能量。对于狭长矩形港湾,假定2b远小于入射波长,所以此时港内只存在纵向振荡,研究问题简化为沿x轴的一维波动。大多数的港湾,其水深都远小于港湾振荡对应的波长。在此情况下,波动基本上是水平的,垂直变化很小。因此,可以利用浅水方程研究这一问题。此时港湾内的波动可以表示为
(1)
在外域(外海),总的波浪场由入射波、被岸线反射回来的反射波以及港湾出口处辐射出来的波浪组成。假设入射波波幅为a0,垂直于岸线进入港湾。外海的整个波浪场可以表示为
(2)

在出口x=0,|y|≤b处,每一点(x′=0,y′)均可认为是一个辐射点源,其辐射的波浪可表示为
(3)
这里r2=(x-x′)2+(y-y′)2,H0(1)(kr)是第一类0阶Hankel函数,参数Q(y′)为港湾出口处的源汇强度系数。整个外域辐射波可以由沿出口边界上分布的所有点源辐射波线性叠加得到
′.
(4)
内外域自由水面及其导数在出口x=0处连续,有
(5)
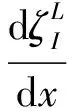
(6)
当kr≪1时,H0(1)(kr)有渐近式
(7)
式中,γ=1.781 072 4…,是Euler常数的指数。式(7)代入式(6)得
-Aksink(x+L)
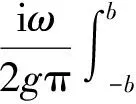
(x→0+, |y| (8) 注意到x→0+时,有 (9) 将式(9)代入式(8)后,得 (10) 可见,在b很小时,源汇强度Q是与y和y′无关的常数。 (11) 即 (12) 对上式右侧中的包含Hankel函数项应用近似式(7),得到 (13) 将式(13)和式(10)代入式(12),可得 (14) 式(14)表明港内波动与外海入射波要素及港湾长度与水深密切相关,虚数i表示二者存在相位差。通常将港内波幅与2倍的外海入射波幅的比值称为放大因子,即 (15) 图2 水波传入港湾示意图Fig.2 Wave propagation into the harbor 图3 港湾放大因子R随kL的变化(b/L=0.1)Fig.3 Amplification coefficient versus kL (b/L=0.1) 图3所示为狭长矩形港湾的放大因子随入射波波数变化情况。当入射波与港湾平面几何尺度和港内地形情况满足一定关系时(即达到共振条件时),港内波高出现极大值,在同一港湾,有多个极大值出现的情况。通常,对于最小波数对应的极大值情形称为第一模态,或者基本模态,它是实际港湾中最常见,通常也是能量最大的模态。对应于第二、三小波数对应的极大值出现的情形,分别称为第二模态、第三模态,以此类推。 港湾共振的研究早在第二次世界大战就已经开始了。为了安全有效地运输军用物资和人员,一些重要港口都开始监测港内外水面波动,并结合气象资料实施预报[10]。为了深入了解这些共振的产生机理,早期的学者从不同的波浪理论上描述这一现象。Miles和Munk[11]讨论了直接与外海相连的矩形港湾共振问题,并引用了辐射阻尼的概念,即波浪进入港口后,口门处产生向外辐射的波浪带走港内部分能量使得港内波高减小。辐射阻尼的概念在港湾共振研究中产生了深远影响,后来的许多理论研究都引用了该方法。但是他们的结果导致波浪进入开口较小的港湾后被捕获在港内而无法传播出去,得到口门越小共振越大的结论,即“港湾佯谬”。这一现象同样出现于公式(15),当港湾特别窄时,即b→0时,放大因子区域无穷大,这显然与实际相悖。这一结果在当时引起了很大争议,激发了更多的学者研究港湾共振这一现象。LeMehaute[12]认为这一佯谬与流体力学中的D′Alembert佯谬有相似之处,因为港口变窄时摩擦带来的波能耗散越来越重要,如果在方程中引入黏性能量耗散则可以避免这样的结果。Ippen和Goda[13]采用傅里叶变换的方法求解了与外海相连的矩形港口内的共振问题。Carrier等[14]在研究通过狭长河道与外海相连的港口内水波共振问题时发现,河道的有限长度所产生的效应定性等同于口门宽度的缩小。Mei和Ünlüata[15]通过分析两个连通港口内的共振现象研究了外港对内港的庇护效应,发现在某些条件下外港不仅不能减缓内港的共振反而有加剧的效果。Yu[16]研究发现如果在港口的上游有河流流入能明显削弱港湾共振。Miles[17]将流体的速度和压力类比为电压和电流,将港湾共振这一流体力学问题等效为电磁学问题。该方法不仅能研究任意形状的港口,还可以通过电阻元件考虑实际流体的能量耗散,且通过电路实验可以模拟真实港湾的共振问题。这些早期的研究主要关注于港内外水深相同的情况,由Wilson[2]和Miles[3]在他们的综述中做了详细的总结和评论。虽然这些早期的研究大多分析形状规则的常水深港湾共振问题,很少能直接应用于实际工程中,但是它们对认识港湾共振的机理有着重要的意义。 近期,Wang等[18]从理论上研究了变水深矩形港口内纵向(沿港口方向)共振问题、分析了地形对其影响,并指出由于折射效应在变水深港口内存在着类似边缘驻波的横向共振。其后又相继给出了港内地形为双曲余弦形式[19]和指数型地形[20]港湾内纵向及横向共振理论。这些变水深港湾横向振荡的能量主要局限于港湾后部水深较浅区域。对于模态(n,m)的横向共振,在离岸方向有m条平行于岸线方向的波节线,在沿岸方向有n条垂直于岸线方向的波节线(图4)。 诱发港湾共振的动力因素是多种多样的,包括波群(次重力波)、海啸、海洋内波、边缘波、剪切流及气象长波等。由于港湾共振的周期较长,普通的风浪和涌浪很难直接引起长周期的共振,而它们所组成的波群(或者是通过非线性相互作用产生的次重力波)周期却在30~300 s之间,处于港口的共振周期范围。Bowers[21]、Mei与Agnon[22]和Wu与Liu[23]先后通过不同的数学方法证明波群及约束于其中的次重力波可以在非线性作用下引起长周期港湾共振,Girolamo[24]通过模型实验验证了这一结论。Okihiro与Guza[25]研究夏威夷的Barbers Point港时发现,外海次重力波能量仅为全部能量的1%,而港内次重力波能量达75%,他们认为是次重力波在港内的共振导致了这一现象。 由水下地震、火山爆发或水下塌陷和滑坡等地壳运动引起的海啸可以激发港湾共振早已得到了证实。海啸的英文Tsunami就是直接从日语音译而来的,表示“港内波浪”的意思。这是由于日本是一个经常遭受海啸侵袭的国家,一些产生于太平洋中部或南、北美洲的海啸横穿整个大洋到达日本,虽然经过如此长距离的传播能量基本耗散殆尽,但是在某些港湾依然会激发很大的共振。1994年11月3日美国阿拉斯加Skagway港东侧一段长250 m的在建码头崩坍入水引起局部海啸,使得港内出现最大波高超过2 m、周期约为3 min的共振,造成约2000万的经济损失并导致一名港口工人的身亡[26]。1995年10月9日在距离墨西哥Manzanillo港25 km处的西海岸发生了8级地震,地震引发的海啸在10~12 min后传入港内,引起该港口及其潟湖内出现周期为36 min、最大波高达2 m持续了近24 h的共振[27]。2004年12月26日印尼苏门答腊特大海啸历时2 h传入距离震源1 700 km的斯里兰卡Colombo港,引起当地出现周期约为75 min,最大波高为3.87 m持续数十天的波动,并历时14 h传入距离震源5 000 km的澳大利亚Bunbury港引起当地出现最大波高为1.75 m的共振[28]。海底地震或滑坡等激发的冲击波通常包括具有孤立波特性的波浪成分和具有色散波特性的波浪成分。Dong等[29]通过模型试验研究发现只有孤立波特性的波浪成分在港湾振荡中起着重要作用,而具有色散波特性的波浪成分没有在港湾内被捕获和放大。此外,王培涛等[30]通过模拟2011年日本东北地震海啸激发大洗町、希洛及陶兰加等港口内的共振现象,发现半封闭港湾使得海啸波被明显放大,且在港口附近出现明显的水平涡并伴随激流现象(图5)。他们认为目前的海啸预警仅关注于海啸的波高是明显不够的,应该考虑其在海湾内的共振放大效应以及相应的激流问题。 图4 波数对应的前4个横向振荡模态波幅空间分布Fig.4 Spatial structure in the harbor for the first four modes 图5 2011年日本东北地震海啸引起大洗町和希洛港区附近的涡流特征Fig.5 Eddy current within CHO and Hilo harbor during 2011 Tohoku earthquake tsunami 大尺度的港湾共振(周期为O(100 min))与外海上空气团的移动和大气压力波动有关。我国东海出现台风时,日本志布志港(Port of Shibushi)会出现周期为数分钟的振荡。这些振荡使得停泊在其内的游艇发生相同周期的大幅晃动[31]。产生于北海的暖湿气团引起该区域风速和气压的波动,随之产生向海岸传播的长周期波浪,最终引起荷兰鹿特丹港出现周期约为90 min的振荡现象[32]。阿曼的萨拉拉港(Port of Salalah),世界上最大的集装箱转运码头之一,在夏季风到来时会发生港内自由水面剧烈晃动现象,影响港内舰船泊稳并降低了港口的货物转运效率[33]。西班牙的Ciutadella港每年夏季都会出现振幅为1 m左右的港湾振荡现象。2006年6月15日出现了振幅为5 m左右的港湾振荡,导致停泊其内的多艘船只受损。此外,在Menorca岛上Platja Gran港与Ciutadella港相邻,两个港内的振荡不仅受自身几何形状及地形的影响,彼此间还相互影响[34]。 产生于两层密度不同的流体中的大洋内波传播到近岸,可引起附近港口内的共振。由于这些内波随着季节变化,因其激发的港湾共振也呈季节性变化。斯里兰卡的Trincomalee湾在春秋季存在周期为42 min左右的较大振动,这些共振呈现出每周两次的周期变化,研究表明它们是由与当地潮汐相关的内波引起的[35]。边缘波是指由于折射作用而被俘获在岸线附近的波浪,一些学者认为近岸波浪中80%以上为边缘波。由于这些波浪平行于岸线传播,很容易引起沿岸开口的港口内的共振。如台湾东海岸的花莲港,每当台风来袭港内都会出现大幅的振荡。通过现场观测、模型实验及数值模拟表明台风引起的波浪由于地形折射作用在近岸形成边缘波,这些边缘波传入港内形成港湾共振[36]。此外,如空气吹过风琴而引起其管内空气共振一样,流速较强的流经过口门也可引起港内共振。Fabrikant[37]从不稳定性理论分析证明了剪切流也能激发港湾振荡。 研究港湾共振的产生机理及激发动力不仅拓展了学术界对该现象的认知,也为如何消弱或避免其危害提供理论基础。通常引起港湾共振的都是周期较长的波浪,具有极强的穿透力,并且波速较大,在水平方向上水的流动性很大,具有相当大的能量。港湾共振最常见也是最主要的危害是对停泊在其内船舶的影响。杨宪章[38]以毛里塔尼亚友谊港为例,研究改善系泊状态的方法。外海周期为78 s、最大波高仅为0.1 m的波浪就可以引起该港内万吨级货轮1.4 m的横摇及1.15 m的纵荡。研究表明传统的防浪手段如减小防波堤某高程以上的孔隙率、码头下加挡浪板、码头下悬挂缓冲重块以及改变系缆状态等都达不到很好的效果。如1994年9月18日的“9424号”台风引起Tomakomai港外出现3 m以上的大浪,由于防波堤的掩护港内的波浪不超过0.5 m。然而停泊在码头的“E.P.”运煤船却出现了振幅达4.5 m周期约为150 s的纵摇,导致数跟缆绳断裂。事后研究发现150 s正是该港的共振周期,也即船舶与港湾发生了共振[39]。位于加利福尼亚洲西南沿海San Pedro湾内的Port of Long Beach一直存在着长周期的共振波浪,特别是从1992年后J泊位作为马士基航运线的货柜码头后,经常出现油轮达3 m以上、周期为数分钟的纵荡。为了深入研究该区域的港湾共振现象,当局聘请了包括Robert Dean,C. C. Mei和Frederic Raichlen等著名的波浪专家组成技术委员会研究这一现象。通常,一艘马士基S级集装箱船(6000 TEU)的纵摇周期为100 s,长滩港J泊位的主要共振周期为130 s左右,正好与船舶的周期接近,所以引起大幅晃动。后来通过在港区外增建防波堤,使得该泊位的共振周期转移到170 s,大大改善了该处的泊稳情况[40]。当然,历史上也不乏失败的例子。如南非开普敦桌湾港的Duncan码头、Victoria码头和Alfred码头存在着周期在1~8 s的共振,引起其内泊船的大幅晃动并导致港池口门出现激流影响通航安全。为了改善港内泊稳情况,在港外增建了防波堤。结果适得其反,防波堤与岸线组成新的共振系统,由于该系统的共振周期与港湾的共振周期非常接近,进一步加剧了该港的水波共振情况[41]。 通常评估港湾共振危害时都将外海波浪在港内共振时放大因子最大的共振模态为最危险共振,在港口的设计及运行中优先关注。Bellotti[42]以意大利Rome游艇码头为例研究发现不同的共振模态在由静止到振幅最大的响应过程历时是不同的,有些放大因子特别大的共振模态其响应时间也特别久,考虑到外海激发动力通常不会持续如此漫长的时间,他建议更应该关注那些响应时间较短的共振模态。Dong等[43]的研究也证实了Bellotti的结论,且进一步发现一旦港湾共振产生后,即使没有外海能量输入,它们也能持续很久,因此还建议关注那些耗散较慢的共振模态。 为了验证港湾共振的产生机理及其诱发因素,许多学者进行了模型试验。室内造波机产生的波浪传到模型港后有部分能量会被反射回来,影响模型试验的造波精度,需要在波浪水槽或港池中的港湾共振试验采用考虑波浪二次反射的主动吸收反射波的造波技术[44]。因此有的试验在模型港外布置有效的消波措施防止二次反射[11, 24]。 尽管物理模型试验是大家公认最为可信的研究方法,然而受试验条件和技术的限制,目前还很难直接模拟各种气象因素引起的港湾共振。此外,一些海啸、边缘波及次重力波引起的港湾共振也需要采取各种处理措施,往往成本很高且需花费大量的时间。因此,许多学者建立各种不同的数值模型来研究这一现象。早期学者多使用Helmholtz方程(常水深情况下)和缓坡方程(缓变水深情况下)建立数值模型。Hwang和Tuck[45]基于对一个奇异积分方程的数值求解,解决了对于任意形状、常水深港口的港湾共振问题。随后,Lee[46]通过使用边界元方法对Helmholtz方程进行求解,也对任意形状、常水深港池共振问题进行了研究。Lee和Raichlen[47]对这一计算程序进行了进一步的优化,考虑了多港池联结的港口共振问题。Olsen和Huang[48]随后提出了一个数值方法来确定任意形状、变水深港池的共振反应。Berkhoff[49]提出了综合考虑波浪折射-绕射的二维缓坡方程,学者们建立了相应的有限单元数值模型,可以高效方便地应用于各种形状和地形条件下的港湾共振问题[50-51]。由于这些数值模型的简单性和可靠性,它们已被广泛地使用于确定新建港口平面规划和已建港口改扩建方案过程中。Helmholtz方程和缓坡方程均属于线性方程,无法准确模拟波浪在传播过程中不同频率波浪在非线性相互作用下的能量传递过程,因此也无法准确模拟次重力波激发的港湾共振现象以及港内的高次谐波问题。 Peregrine[52]推导了考虑波浪传播过程中非线性相互作用经典Boussinesq方程。然而该方程仅适用于弱非线性弱色散性浅水波,即水深小于波长1/5的范围,无法满足实际工程的需要。为了扩大其适用范围,对经典Boussinesq方程的改进主要是从两方面着手:一是在推导过程中保留更多高阶项,如Madsen和Schaffer[53]、Gobbi等[54]、Zou和Fang[55]和Ataie-Ashtiani和Najiafi Jilani[56]都提出了一系列精确到四阶频散精度的高阶Boussinesq方程以及Lynett和Liu[57]采用两层水体的流速从Euler方程推导出达到同样精度的Boussinesq方程,特别是Madsen等[58]采用自由表面边界条件作为时间演化方程,利用势函数满足的Laplace方程的解析解形式建立了自由表面边界速度和底面边界速度之间的关系,推导了几乎不受水深限制的Boussinesq波浪模型;另一个方法是在经典方程中人为引入一些色散项用于改进方程的色散精度,如Madsen等[59]与Nwogu[60]。这些改进都使得方程的精度得到了不同程度的提高,扩大了它们的应用范围。 这些基于各类Boussinesq方程的波浪模型有些是专门为研究港湾共振开发的[44, 61],而有些模型虽然不是专门为此开发的,但它们依旧可以很好地应用于港湾共振中[62-63]。特别是基于高阶Boussinesq方程的一些模型,如采用曲线坐标和交错网格离散的有差分模型FUNWAVE[64]以及各类采用有限三角形网格的有限元模型[44, 61-62],它们不仅能很好地适应各种复杂边界条件,且能很好地模拟港湾共振的非线性过程。Wang等[65]建立了一个能模拟底床运动产生波浪及波浪传播变形的Boussinesq模型,并用该模型模拟了港内底床运动引起的港湾振荡现象。其研究表明小区域的底床运动引起明显的横向振荡,而纵向振荡很小,而这些横向振荡对运动底床的位置较敏感。运动底床的速度和幅值仅影响港湾振荡的幅值,而不改变港湾振荡中出现的模态成分。Wang等[66]采用FUNWAVE2.0研究了变水深港湾内横向共振的激发原理。他们的研究表明当外海波浪垂直进入变水深港湾时,在一定条件下,发生同频共振和次谐频共振现象,即当入射波的频率与横向共振频率的相同或两倍时可以激发大幅度的横向共振。Dong等[67]采用FUNWAVE2.0模拟了波群引起的狭长矩形港湾内的非线性共振现象,并提出一个港内低频波浪分离方法,分析了港湾处于第一共振模态下锁相长波和自由长波的波幅以及它们相对成分随着短波波长的变化。随后,Gao等[68]在此基础上,进一步研究了港湾处于最低的4个共振模态下入射短波的波长和波幅对港内锁相长波和自由长波的波幅以及它们的相对成分的影响。Gao等[68]使用完全非线性Boussinesq模型FUNWAVE-TVD对N波诱发的瞬变港湾共振进行了模拟,并使用正交模态分解法研究了入射N波波幅的变化和入射N波类型的不同对港内相对波能分布的影响。 由于激发港湾共振的入射波均为长波,传统的长波方程及缓坡方程均可以很好地模拟这一现象,特别是由于这些方程简单易于编程,对于快速评估港湾内的共振周期及相应模态的能量分布较为实用。然而受限于长波方程未考虑波浪的频散性而缓坡方程不能很好地刻画波浪非线性及在剧烈地形过程中的变化,这些模型在精确反演港湾共振中的非线性能量传递以及波浪在陡变地形上的传播过程均有较大误差。Boussinesq模型考虑了波浪的非线性和频散性,可以很好地模拟外海波浪的传播演化及其激发港内共振现象,然而受水深限制,仍然不能考虑波浪在外海深水过程。虽然学者们已经相应提出了可以适用于深水的高阶方程,但这些方程涉及到高阶空间导数,需要复杂的数值求解方式,不仅计算效率低,且数值稳定性较差。 我国夏季为热带低气压控制易受台风侵袭,冬季受西伯利亚冷空气影响北方易出现大风天气,一些港口均会出现振幅较大的共振。由于港湾共振的周期通常远大于风浪和涌浪并小于天文潮,且实测的结果又往往与天文潮叠加在一起,所以有的研究也称之为假潮。这种大幅共振叠加在高、低潮上,引起水位的急骤升降,伴随而来的是流速的急骤变化,形成沿岸渔民常说的“妖流”。如黄海北部的小长山岛[69]和渤海的龙口港[70]均观测到周期为数分钟、振幅可达1 m以上的共振。这些港湾共振事件表明其发生与大气扰动有着密切联系[71]。通常,这些大气扰动包括局地气压和风的突变、台风、雷暴等。我国龙口发现过水位变化幅度达2.93 m的假潮,超过1 m的假潮更是多次发现[70, 72-74]。研究表明这些大幅共振是由龙口港特殊地理环境、港湾及附近大范围海域骤猛的向港爆发性大风尤其强雷暴大风涌水在港内骤然积聚和海水惯性振荡的综合结果。此外,大连的老虎滩[75]同样发现了与大气扰动有关的共振事件。虽然港湾共振与大气扰动有很高的相关性,但是研究表明它们之间的直接耦合共振是不可能的,因为二者的尺度和频率往往不同;通过数值模拟及理论分析表明大气扰动通过外海表面波作为中间机制引起港口内的水波共振[71,74]。 此外,尽管有第一岛链和宽广的大陆架的保护,我国台湾、浙江及福建仍可能受越洋海啸的影响。而中国南部海区域位于环太平洋地震带的边缘,同时面临马尼拉海沟及比邻的环太平洋地震带潜在海啸源的威胁,是国际公认的潜在海啸高风险区。如1992年1月4-5日,我国海南省西南部海域发生最大震级仅3.7级的弱地震群。受其影响榆林湾验潮站记录到波高0.78 m、周期约30 min的海啸波,并引起榆林港内潮水急涨急落(最大流速达1 m/s),导致渔船走锚搁浅或相互磕碰,造成了较大损失[76]。由此可见,对于特定的港湾,地震震级并非控制海啸波高的主要因素,海啸激发的局地共振振幅往往数倍于海啸本身。Yamazaki和Cheung[77]发现2010年智利海啸由于地形俘获效应使得在南美大陆架上形成周期在35 min至129 min之间的陆架波,它们激发了Bay of Concepcin内的第一模态共振,这些陆架波及湾内的共振最终又激发了Talcahuano Harbor的共振,使其在地震发生3 h后出现巨大水体波动现象。本文作者王培涛研究太平洋海啸对我国沿海的影响时发现海啸在我国东海大陆架也会产生周期约为120 min的陆架波,而这些长周期波浪激发的港湾共振必将数倍地放大海啸波能量,对当地产生巨大危害。本文不完全统计了近年来我国沿海发生过共振现象的港湾(图6),其中内陆湖泊表示在此处发生过湖震现象。由图可见,从北向南、包括台湾在内,我国所有沿海省份都有发生共振的港口存在。这仅是作者从已有文献的统计结果,相信依然有很多港湾发生过类似的事件,只是缺乏报道佐证而已。 随着对港湾共振认识的逐渐深入及其对港内船舶安全、港工建设、滩涂开发以及人们的日常涉海活动等带来很大的危害,越来越多的专家学者投入到这一领域。实践证明,对于受长周期波浪影响的海域,如果在港口的设计和建造中对长周期波的特性认识不足,一旦港口建成,再想大幅度减小或消除港湾共振的影响,就非常困难。其主要原因是实际港口地形及形状复杂、外海动力要素各异,很难有统一普适的抑制方法。此外,由于实际情况限制,发生港湾共振的港口通过延长防波堤等措施减弱其危害,费用高昂有时甚至无法实施。因此,在港口的建造之初就考虑港湾共振的影响,并在设计和施工中采取有效的措施防止其发生是最佳选择。特别是对于存在众多港池的港口,各个港池存在其固有周期,综合考虑这些港池共振影响的港口规划设计具有重要意义。近年随着我国承接到越来越多的海外项目,如毛利塔尼塔、斯里兰卡以及韩国等地的港口工程中,均涉及到周期为数十秒的长波问题。虽然目前我国的水文规范中并未考虑到这些长周期波浪的影响,但随着越来越多的工程问题出现,未来的规范中必然要考虑港湾共振的影响。 图6 我国沿海发生过共振现象的港湾Fig.6 Harbor resonance within China 由于港湾共振直接威胁着港内泊船的稳定性,而港内系泊船的缆绳与船舶之间也组成一个共振系统,因此船舶-缆绳系统与港湾的耦合共振一直是本领域的研究热点与难点问题。综合考虑不同荷载情况的船舶及不同锚泊系统受港湾共振的影响,以及港湾共振对通航安全影响,具有重要的应用价值。此外,港湾共振对不同荷载LNG船舶内液舱晃荡的影响也是这一领域的新方向。 对于港湾共振的本质机理研究,从Miles和Munk[11]基于辐射阻尼给出完整的常水深狭长港湾内共振理论后,研究主要基于该思想的进一步完善,直至最近Wang等[18-20]提出受折射作用而在变水深港湾内存在横向共振的现象,丰富了港湾共振理论。实际港湾内的共振不仅受内部地形及形状决定还受外海地形及岸线形状的影响。在一切特殊地形情况下,港外存在的边缘波或陆架波,这些沿岸线传播的能量进一步传入港内引起长波共振。从理论上探讨外海地形对港湾共振的影响是目前港湾共振理论的热点问题。此外,一些港口建于海湾之内,长波不仅在港内存在共振,在海湾也可以激发湾内共振,综合考虑湾与港的耦合共振现象同样具有重要的意义。此外,随着全球海岛资源的开发,一些过去鲜有开发的岛屿上也陆续建设了港口。这些海岛突兀于海洋之中,地形变化剧烈,基于其潟湖所建立的港口掩护较差,综合研究这些海岛港口内的水波共振对于海岛开发具有重要意义。 此外,如前文所示,海啸及气旋过境所伴随的长周期波浪极易在近岸地区激发共振,而目前的海啸与台风灾害预警预报往往忽略了其可以进一步激发局地共振所带来的“放大”效应,极大地低估了这类波浪的危害。因此,在海洋灾害的评估与预报中,结合当地海域地形及海岸资料考虑其进一步激发港湾共振的影响,对于海洋灾害评估及预警预报有着重要意义。 目前,日本已把港湾共振的观测和预报纳入了正常的业务工作,每月正式出版沿岸港口发生共振的时间、周期和振幅等。针对Ciutadella港经常发生共振事件,自1984年以来西班牙国家气象局巴利阿里气象中心就开始利用实时的气象资料对该地区的港湾共振进行预报并向公众发布。他们成功预报了2006年6月15日发生的特大港湾共振事件并提前一天将消息发布给公众,所以当时有多艘游艇毁坏但未造成人员伤亡。虽然我国有众多港口发生过类似的港湾共振事件,但是目前的研究与认识明显不足。历次的海岸资源调查也均未涉及长波共振情况,因此目前我国哪些地区及港口易发生港湾共振事件还不清楚,亟需全面系统的开展实际调查。针对典型港湾,明确其激发因素及共振特征,在此基础上建立相应的预警预报系统,是未来亟需解决的问题与研究方向。 虽然基于长波方程、缓坡方程及Boussinesq方程的数值模型均很成熟,且有众多开源模型,但是由于其理论局限及数值效率的影响,仍无法精确模拟波浪在外海的产生、长距离演化及其进一步激发港内共振的复杂非线性过程。随着计算机效率的提高,学者们提出了直接求解Navier-Stokes方程或欧拉方程的非静压模型[78]。该模型舍弃了高精度捕获波浪自由界面的传统方法,假设自由界面是空间一一映射关系,建立三维数值模型。由于其控制方程空间导数不超过二阶,易于求解,且数值稳定,特别是目前基于多CPU并行或基于显卡GPU并行模型的开发,极大地拓展了其适用范围,将是港湾共振的理想数值模型。 [1] 李培顺, 曹丛华, 王爱莲, 等. 黄、渤海沿岸港湾的假潮及成因探讨[J]. 海洋预报, 2003, 20(4): 5-13. Li Peishun, Cao Conghua, Wang Ailian, et al. Investigation of seiche and its formation causes in harbors along shore of Yellow Sea-Bohai Sea[J]. Marine Forecasts, 2003, 20(4): 5-13. [2] Wilson B W. Seiches[C]//Advances in Hydroscience. New York: Academic Press, 1972: 1-94. [3] Miles J W. Harbor Seiching[J]. Annual Review of Fluid Mechanics, 2003,6(6): 17-33. [4] Rabinovich A B. Seiches and Harbor Oscillations[M]//Handbook of Coastal and Ocean Engineering. New Jersey: World Scientific, 2010: 193-236. [5] VonderMühll K. Uber die bewegung tropfbarer Flüssigkeiten in Gefässen[J]. Mathematische Annalen,1928, 27(4):575-600. [6] 郑金海, 董文凯, 徐龙辉, 等. 正五边形港湾内的水波共振[J]. 河海大学学报(自然科学版), 2014, 42(3): 262-266. Zheng Jinhai, Dong Wenkai, Xu Longhui, et al. Oscillations within a regular pentagon-shaped harbor[J]. Journal of Hohai University:Natural Sciences, 2014, 42(3): 262-266. [7] 张弛, 吴善翔, 王岗, 等. 正六边形及其扩展形状港湾内的水波共振[J]. 计算力学学报, 2015, 32(3): 372-377. Zhang Chi, Wu Shanxiang, Wang Gang, et al. Oscillations within a regular hexagon andits extensional shapes[J]. Chinese Journal of Computational Mechanics, 2015, 32(3): 372-377. [8] 王岗, 郑金海, 徐龙辉, 等. 椭圆形港湾内水波共振的解析解[J]. 工程力学, 2014, 31(4): 252-256. Gang Wang, Zheng Jinhai, Xu Longhui, et al. An analytical solution for oscillations within an elliptical harbor[J]. Engineering Mechanics, 2014, 31(4): 252-256. [9] 李裕澈, 时振梁, 曹学锋. 1597年10月6日“珲春—汪清深震区”M≥8地震触发的湖震和火山喷发[J]. 地震学报, 2012, 34(4): 557-570. Li Yuche, Shi Zhenliang, Cao Xuefeng. The seiches and volcanic eruption triggered by the 6 October 1597 earthquake with M≥8 in the “Hunchun-Wangqing, Northesatern China, deep-focus seismic zone”[J]. Acta Seismologica Sinica, 2012, 34(4): 557-570. [10] Vanoni V A, Carr J H. Harbor Surging[C]//Proceedings of First Conference on Coastal Engineering, Long Beach. 1950: 60-68. [11] Miles J, Munk W. Harbor paradox[J]. Journal of Waterways and Harbors Division, 1961, 87: 111-130. [12] LeMehaute B. Theory of wave agitation in a Harbor[J]. Journal of the Hydraulics Division, 1961, 87:31-50. [13] Ippen A T, Goda Y. Wave induced oscillations in harbors: the solution for a rectangular harbor connected to the open sea[R]. Massachusetts Inst of Tech Cambridge Hydrodynamics Lab,1963. [14] Carrier G F, Shaw R P, Miyata M. Channel effects in harbor resonance[J]. Journal of Engineering Mechanics, 1971, 97:1703-1716. [15] Mei C C, Ünlüata Ü. Resonant scattering by a harbor with two coupled basins[J]. Journal of Engineering Mathematics, 1976, 10(4): 333-353. [16] Yu X P. Oscillations in a coupled bay-river system.1. Analytic solution[J]. Coastal Engineering, 1996, 28(1/4): 147-164. [17] Miles J W. Resonant response of harbours: an equivalent-circuit analysis[J]. Journal of Fluid Mechanics, 1971, 46(2): 241-265. [18] Wang G, Dong G H, Perlin M, et al. An analytic investigation of oscillations within a harbor of constant slope[J]. Ocean Engineering, 2011, 38(2): 479-486. [19] Wang Gang, Zheng Jinhai, Liang Qiuhua, et al. Analytical solutions for oscillations in a harbor with a hyperbolic-cosine squared bottom[J]. Ocean Engineering, 2014, 83(2): 16-23. [20] Wang Gang, Zheng Jinhai, Liang Qiuhua, et al. Theoretical analysis of harbor resonance in harbor with an exponential bottom profile[J]. China Ocean Engineering, 2015, 29(6): 821-834. [21] Bowers E C. Harbor resonance due to set-down beneath wave groups[J]. Journal of Fluid Mechanics, 1977, 79(1): 71-92. [22] Mei C C, Agnon Y. Long-period oscillations in a harbour induced by incident short waves[J]. Journal of Fluid Mechanics, 1989, 208: 595-608. [23] Wu J K, Liu P L F. Harbour excitations by incident wave groups[J]. Journal of Fluid Mechanics, 1990, 217: 595-613. [24] Girolamo P D. An experiment on harbour resonance induced by incident regular waves and irregular short waves[J]. Coastal Engineering, 1996, 27(1/2): 47-66. [25] Okihiro M, Guza R T. Observations of seiche forcing and amplification in three small harbors[J]. Journal of Waterway Port Coastal and Ocean Engineering, 1996, 122(5): 232-238. [26] Kulikov E A, Rabinovich A B, Thomson R E, et al. The landslide tsunami of November 3, 1994, Skagway Harbor, Alaska[J]. Journal of Geophysical Research: Oceans, 1996, 101: 6609-6615. [27] Carbajal N, Galicia-Pérez M A. Earthquake-induced helmholz resonance in Manzanillo Lagoon, Mexico[J]. Revista Mexicana de Física, 2002, 48: 192-196. [28] Pattiaratchi C B, Wijeratne E M. Tide gauge observations of 2004-2007 Indian Ocean tsunamis from Sri Lanka and Western Australia[J]. Pure and Applied Geophysics, 2009, 166: 233-258. [29] Dong Guohai, Wang Gang, Ma Xiaozhou, et al. Harbor resonance induced by subaerial landslide-generated impact waves [J]. Ocean Engineering, 2010, 37: 927-934. [30] 王培涛, 闪迪, 王岗, 等. 日本东北Mw9.0地震海啸在港池及邻近区域诱发的涡流危险性计算与评估分析[J]. 地球物理学报, 2016, 59(11): 4162-4177. Wang Peitao, Shan Di, Wang Gang, et al. Modelling and assessment of tsunami-induced vortex flows hazards from the 2011MW9.0 Tohoku-oki earthquake in harbors and adjacent area[J]. Chinese Journal of Geophysics, 2016, 59(11): 4162-4177. [31] Uzaki K I, MatsunagaN, Nishii Y, et al. Field observations and numerical simulations of harbor oscilations due to long period waves[C]//Proceedings of the 29th international conference on coastal engineering, Portugal. 2004: 1264-1276. [32] de Jong M P C, Battjes J A. Seiche characteristics of Rotterdam harbour[J]. Coastal Engineering, 2004, 51(5/6): 373-386. [33] Carr C M, Yavary M, Yavary M. Wave agitation studies for port expansion—Salalah, Oman[C]//Port Development in the Changing World. 2004, 136: 1-10. [34] Marcos M, Liu P L F, Monserrat S. Nonlinear resonant coupling between two adjacent bays[J]. Journal of Geophysical Research Oceans, 2004, 109: C05008. [35] Wijeratne E M S, Woodworth P L, Pugh D T. Meteorological and internal wave forcing of seiches along the Sri Lanka coast[J]. Journal of Geophysical Research Oceans, 2010, 115: C03014. [36] Chen G Y, Chien C C, Su C H, et al. Resonance induced by edge waves in Hua-Lien Harbor[J]. Journal of Oceanography, 2004, 60: 1035-1043. [37] Fabrikant A L. Harbour oscillations generated by shear flow[J]. Journal of Fluid Mechanics, 1995, 282: 203-217. [38] 杨宪章. 长周期波的特性及对系泊船舶动态特性的影响[J]. 港口工程, 1989(6): 37-43. Yang Xianzhang. The characteristics of long period wave and the influence on the dynamic characteristics of mooring ship[J]. Harbour Engineering, 1989(6): 37-43. [39] Van Der Molen W, Monardez P, Van Dongeren A P. Numerical simulation of long-period waves and ship motions in Tomakomai port, Japan[J]. Coastal Engineering Journal, 2006, 48(1): 59-79. [40] Briggs M J, Dykstra D, Baldwin T. Modeling of harbor resonance in port of long beach[C]//International Conference on Civil Engineering in the Oceans, American Society of Civil Engineers, Baltimore. 2006: 479-493. [41] Darbyshire M. Long waves on the coast of the Cape Peninsula[J]. Deutsche Hydrographische Zeitschirift, 1963, 16(4): 167-185. [42] Bellotti G. Transient response of harbours to long waves under resonance conditions[J]. Coastal Engineering, 2007, 54: 680-693. [43] Dong Guohai, Wang Gang, Ma Xiaozhou, et al. Numerical study of transient nonlinear harbor resonance[J]. Science China-Technological Sciences, 2010, 53(2): 558-565. [44] Losada I J, Gonzalez-Ondina J, Diaz-Hernandez G, et al. Numerical modeling of nonlinear resonance of semi-enclosed water bodies: Description and experimental validation[J]. Coastal Engineering, 2008, 55(1): 21-34. [45] Hwang L S, Tuck E O. On the oscillations of harbours of arbitrary shape[J]. Journal of Fluid Mechanics, 1970, 42(3): 447-464. [46] Lee J J. Wave-induced oscillations in harbours of arbitrary geometry[J]. Journal of Fluid Mechanics, 1971, 45(2): 375-394. [47] Lee J J, Raichlen F. Wave induced oscillations in harbors with connected basins[R]. California Institute of Technology, Pasadena, CA., 1971. [48] Olsen K, Huang L S. Oscillations in a bay of arbitrary shape and variable depth[J]. Journal of Geophysical Research, 1971, 76(21): 5048-5064. [49] Berkhoff J C W. Computation of combined refraction diffraction[C]//Proceedings of the 13th International Conference on Coastal Engineering. 1972: 471-490. [50] 邹志利. 水波理论及其应用[M]. 北京: 科学出版社, 2005. Zou Zhili. Water Wave Theories and Their Applications[M]. Bejing: Science Press, 2005. [51] Panchang V, Chen W, Xu B, et al. Exterior bathymetric effects in Elliptic Harbor wave models[J]. Journal of Waterway Port Coastal and Ocean Engineering, 2000, 126(2): 71-78. [52] Peregrine D H. Long waves on a beach[J]. Journal of Fluid Mechanic, 1967, 27: 815-827. [53] Madsen P A, Schaffer H A. Higher-order Boussinesq-type equations for surface gravity waves: derivation and analysis[J]. Philosophical Transactions of the Royal Society of London Series A-Mathematical Physical and Engineering Sciences, 1998, 356: 3123-3181. [54] Gobbi M F, Kirby J T, Wei G. A fully nonlinear Boussinesq model for surface waves. Part 2. Extension to O(kh)(4)[J]. Journal of Fluid Mechanics, 2000, 405: 181-210. [55] Zou Z L, Fang K Z. Alternative forms of the higher-order Boussinesq equations: Derivations and validations[J]. Coastal Engineering, 2008, 55(6): 506-521. [56] Ataie-Ashtiani B, Najafi Jilani A. A higher-order Boussinesq-type model with moving bottom boundary: applications to submarine landslide tsunami waves[J]. International Journal for Numerical Methods in Fluids, 2007, 53(6): 1019-1048. [57] Lynett P, Liu P L F. A two-layer approach to wave modelling[C]//Proceedings of The Royal Society of London A: Mathematical, Physical and Engineering Sciences. The Royal Society, 2004, 460: 2637-2669. [58] Madsen P A, Bingham H B, Liu H. A new Boussinesq method for fully nonlinear waves from shallow to deep water[J]. Journal of Fluid Mechanics, 2002, 462: 1-30. [59] Madsen P A, Murray R, Sørensen O R. A new form of the Boussinesq equations with improved linear dispersion characteristics. Part 2. A slowly-varying bathymetry[J]. Coastal Engineering, 1991, 15(4): 371-388. [60] Nwogu O. Alternative form of Boussinesq equations for nearshore wave propagation[J]. Journal of Waterway Port Coastal and Ocean Engineering, 1993, 119: 618-638. [61] Woo S B, Liu P L F. Finite-element model for modified Boussinesq equations. Ⅱ: Applications to nonlinear harbor oscillations[J]. Journal of Waterway Port Coastal and Ocean Engineering, 2004, 130: 17-28. [62] Walkley M, Berzins M. A finite element method for the two-dimensional extended Boussinesq equations[J]. International Journal for Numerical Methods in Fluids, 2002, 39(10): 865-885. [63] Kirby J T. Boussinesq models and applications to nearshore wave propagation, surf zone processes and wave-induced currents[M]//Advances in Coastal Modeling. Elsevier, 2003: 1-41. [64] Kirby J T, Long W, Shi F. Funwave 2.0 fully nonlinear boussinesq wave model on curvilinear coordinates[R]. Newark: Center for Applied Coastal Research Dept. of Civil & Environmental Engineering, University of Delaware, 2003. [65] Wang G, Dong G H, Perlin M, et al. Numerical investigation of oscillations within a harbor of constant slope induced by seafloor movements[J]. Ocean Engineering, 2011, 38(17/18): 2151-2161. [66] Wang Gang, Zheng Jinhai, Maa J P Y, et al. Numerical experiments on transverse oscillations induced by normal-incident waves in a rectangular harbor of constant slope[J]. Ocean Engineering, 2013, 57(2): 1-10. [67] Dong G H, Gao J L, Ma X Z, et al. Numerical study of low-frequency waves during harbor resonance[J]. Ocean Engineering, 2013, 68(8): 38-46. [68] Gao Junliang, Ji Chunyan, Gaidai O, et al. Numerical study of infragravity waves amplification during harbor resonance[J]. Ocean Engineering, 2016, 116: 90-100. [69] 李坤平, 陈则实. 小长山港内港湾假潮变化的基本特征[J]. 黄渤海海洋, 1999, 17(3): 10-15. Ling Kunping, Chen Zeshi. Statistical characteristics of variations in seiches in Xiao Changshan Harbour[J]. Journal of Oceanography of Huanghai & Bohai Seas, 1999, 17(3): 10-15. [70] 王兴铸, 李坤平, 余宙文. 龙口港内港湾振动的概要特征[J]. 海洋湖沼通报, 1986(2): 1-5. Wang Xingchou, Ling Kunping, Yu Zhouwen. Statistical characteristics of seiches in Longkou harbour[J]. Transactions of Oceanology and Limnology, 1986(2): 1-5. [71] 夏综万, 林少奕, 王永信, 等. 南海北部沿岸海洋站的假潮[J]. 海洋与湖沼, 2002, 33(1): 8-14. Xia Zongwan, Lin Shaoyi, Wang Yongxin, et al. Seiches at the coastal stations along the north coast of south China sea[J]. Oceanologia et Limnologia Sinica, 2002, 33(1): 8-14. [72] 李培顺, 曹丛华, 江崇波, 等, 龙口港的假潮及成因探讨[J]. 海洋通报, 2003, 22(5): 1-8. Li Peishun, Cao Chonghua, Jiang Congbo, et al. Discussion on the seiche in the Longkou harbour and its causes of formation[J]. Marine Science Bulletin, 2003, 22(5):1-8. [73] 刘赞沛, 陈则实, 宋万先, 等. 龙口港湾大振幅假潮的成因分析[J]. 海洋学报, 2001, 23(1): 120-126. Liu Zanpei, Chen Zeshi, Song Wanxian, et al. A cause giving rise to large amplitude seiches in the Longkou Bay[J]. Haiyang Xuebao, 2001, 23(1): 120-126. [74] 王钟桾. 龙口湾大振幅假潮形成的数值模拟[J]. 黄渤海海洋, 2000, 18(3): 7-13. Wang Zhongjun. The numerical modelling of seiches of large amplitude in Longkou Bay[J]. Journal of Oceanography of Huanghai & Bohai Seas, 2000, 18(3): 7-13. [75] 刘赞沛, 陈则实, 邹娥梅, 等, 大连老虎滩澳的大振幅假潮[J]. 海洋学报, 2000, 22(2): 125-131. Liu Zanpei, Chen Zeshi, Zou Emei, et al. Seiches of large amplitude in the inlet of the Laohutan beach Dailian city [J]. Haiyang Xuebao, 2000, 22(2): 125-131. [76] 于福江, 原野, 赵联大, 等. 2010年2月27日智利8.8级地震海啸对我国影响分析[J]. 科学通报, 2000, 56(3): 239-246. Yu Fujiang, Yuan Ye, Zhao Lianda, et al. Evaluation of potential hazards from teletsunami in China: Tidal observations of a teletsunami generated by the Chile 8.8Mw earthquake[J]. Chinese Science Bulletin, 2000, 56(3): 239-246. [77] Yamazaki Y, Cheung K F. Shelf resonance and impact of near-field tsunami generated by the 2010 Chile earthquake[J]. Geophysical Research Letters, 2011, 38(12):564-570. [78] 王岗, 郑金海. 非静压模波浪模型新理论[C]//第十七届中国海洋(岸)工程学术讨论会论文集. 北京: 海洋出版社, 2015: 763-772. Wang Gang, Zheng Jinhai. A new theory of non-static die-wave model[C]//Proceedings of the 17th Symposium on Chinese Ocean (Coastal) Engineering. Beijing: China Ocean Press, 2015: 763-772. Review on harbor resonance Wang Gang1,4, Gao Junliang2, Wang Peitao3, Zheng Jinhai1,4, Dong Guohai5 (1.KeyLaboratoryofCoastalDisasterandDefence,MinistryofEducation,HohaiUniversity,Nanjing210098,China; 2.SchoolofNavalArchitecture&OceanEngineering,JiangsuUniversityofScienceandTechnology,Zhenjiang212003,China; 3.NationalMarineEnvironmentalForecastingCenter,Beijing100081,China; 4.CollegeofHarborCoastalandOffshoreEngineering,HohaiUniversity,Nanjing210098,China; 5.StateKeyLaboratoryofCoastalandOffshoreEngineering,DalianUniversityofTechnology,Dalian116023,China) Harbor resonance is phenomenon that large oscillations within the harbor are forced at one or more of its natural frequencies. It is crucial in the locally coastal hydrodynamics and ship navigation, and further affect the protection and evaluation of water disaster. This paper presents an overview of harbor resonance and seiches, including resonance mechanism, external forcing and simulation methods. Several typical events in China have been detailed, especially for their resonance characteristics and generation mechanisms. Finally, several prospects are put forward based on the coastal characteristics and current research foundation. harbor resonance; seiches; wave resonance; water wave theory TV139.2 A 0253-4193(2017)11-0001-13 王岗,高俊亮,王培涛, 等. 港湾共振研究综述[J]. 海洋学报, 2017, 39(11): 1-13, 10.3969/j.issn.0253-4193.2017.11.001 Wang Gang, Gao Junliang, Wang Peitao, et al. Review on harbor resonance[J]. Haiyang Xuebao, 2017, 39(11):1-13, doi:10.3969/j.issn.0253-4193.2017.11.001 2016-10-12; 2017-02-20。 国家重点研发计划(2017YFC1404205);国家自然科学基金面上项目(51579090);国家自然科学基金杰出青年科学基金项目(51425901);国家自然科学基金青年项目(51609108,51209081)。 王岗(1982—),男,河北省张家口市人,博士,主要从事港湾共振、水波模拟及海啸与洪水风险评估研究。E-mail:gangwang@hhu.edu.cn *通信作者:郑金海,教授,主要从事河口海岸动力学基础理论与模拟方法研究。E-mail:jhzheng@hhu.edu.cn
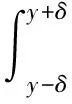

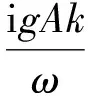

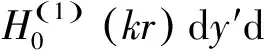



3 激发因素


4 模拟方法
5 我国的港湾共振
6 展望


