SWAN模型中不同风拖曳力系数对风浪模拟的影响

丁磊，于博

(1.天津科技大学 海洋与环境学院，天津 300457；2.天津市海洋环境与修复技术工程中心，天津 300457)

SWAN模型中不同风拖曳力系数对风浪模拟的影响

丁磊1，2，于博1

(1.天津科技大学 海洋与环境学院，天津 300457；2.天津市海洋环境与修复技术工程中心，天津 300457)

本文以荷兰哈灵水道海域为实验区域，通过敏感性实验，研究了在14 m/s、31.5 m/s和50 m/s(分别代表一般大风、强热带风暴和强台风的极端条件)定常风速下SWAN模型中不同风拖曳力系数对风浪模拟的影响程度。结果表明，对于近岸浅水区域(水深小于20 m)，风拖曳力系数计算方案的选择对有效波高影响较小，而且当风速增加到一定程度后，波浪破碎成为影响波高值的主要因素；对于深水区域(水深大于30 m)，一般大风条件下风拖曳力系数计算方案的选择对有效波高影响仍然较小，随着风速的继续增大，风拖曳力系数计算方案的选择对有效波高的影响逐渐显著。对于平均周期，风拖曳力系数计算方案的选择和风速的改变对其影响均较小，而由水深变浅导致的波浪破碎对其影响较为显著。根据敏感性实验结果，本文对SWAN模型中风拖曳力系数计算方案的选择做出如下建议：计算近岸浅水区域风浪场或深水区域一般大风条件风浪场时，其风拖曳力系数可以直接采用模型默认选项；而对于深水区域更大风速条件，可首先采用模型默认选项试算，然后结合当地海域实测波浪资料进行修正。

风拖曳力系数；SWAN模型；风浪模拟；有效波高；平均周期

1 引言

作为第三代风浪模型的代表，SWAN模型在理论研究和工程实践中得到了越来越广泛的应用[1-5]。风是驱动海面波浪最重要的动力因子，模型中风能输入对于波浪成长的影响是通过式(1)来实现的。

(1)

式中，τa为风应力；ρa为空气密度；CD是风拖曳力系数；U*和U10分别是摩阻风速和距海面10 m处风速。由此可见，风拖曳力系数是决定波浪计算精度的关键参数之一。当前，风拖曳力系数有多种参数化方案，但大多表示成关于U10的一次函数形式[6]。其中较为常用的计算方案有：Garratt[7]给出的式(2)、Large和Pond[8]给出的式(3)(以下简称LP)以及Wu[9]给出的式(4)(以下简称WU)。

CD=(0.75+0.067U10)×10-3，

(2)

(3)

(4)

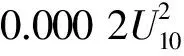
同时，也有学者采用关于U10的单个二次函数来表示风拖曳力系数的变化，得到通式：

(5)

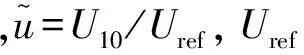
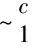
(6)

在这些风拖曳力系数计算方案中，最新SWAN模型(41.10)提供了3种选择：WU、FIT和SWELL。同时，也可以在WU的基础上增加上限值，SWAN模型用户手册[18]中推荐该值为2.5×10-3(以下简称WU-cap 2.5)。图1显示了SWAN模型采用的各风拖曳力系数随风速的变化过程，其中WU-cap 2.0是借鉴Huang等[19]的工作，将WU的上限值调整为2.0×10-3。另外，由于SWELL中系数的取值与波浪方向分布的宽度σθ相关，这里仅给出σθ≤30°或σθ≥80°条件下风拖曳力系数的变化。可见，各计算方案间的变化趋势差异较为明显，尤其是在风速超过一定数值之后。例如，FIT相比于WU在风速超过32.6 m/s时减小超过30%。因此，比较SWAN模型中不同风拖曳力系数对风浪模拟的影响效果对于提高模型的计算精度具有重要的科学意义和应用价值。Huang等[19]研究了WU、WU-cap 2.5、WU-cap 2.0、LP-cap 2.115和LP OEY对飓风条件下SWAN模型模拟的影响效果，结果显示WU和WU-cap 2.5会高估深水有效波高，建议使用WU-cap 2.0或者LP OEY。除此之外，仍然缺乏对SWELL和取代WU成为新版本SWAN模型默认选项FIT的系统性比较。因此，本文将对SWAN模型(41.10)中的WU、WU-cap 2.0、WU-cap 2.5、FIT和SWELL的影响效果进行比较，为今后SWAN模型使用过程中风拖曳力系数计算方案的选择提供参考。

图1 风拖曳力系数变化过程Fig.1 Variation of wind drag coefficients

2 模型配置与验证

图3显示了SWAN模型结果与实测数据的比较结果，图中分别比较了有效波高和平均周期。两者总体上符合较好，特别是模型很好地反映了波浪向岸传播过程中经过浅滩发生破碎前后有效波高的变化，从而验证了SWAN模型对实验区域的适用性。

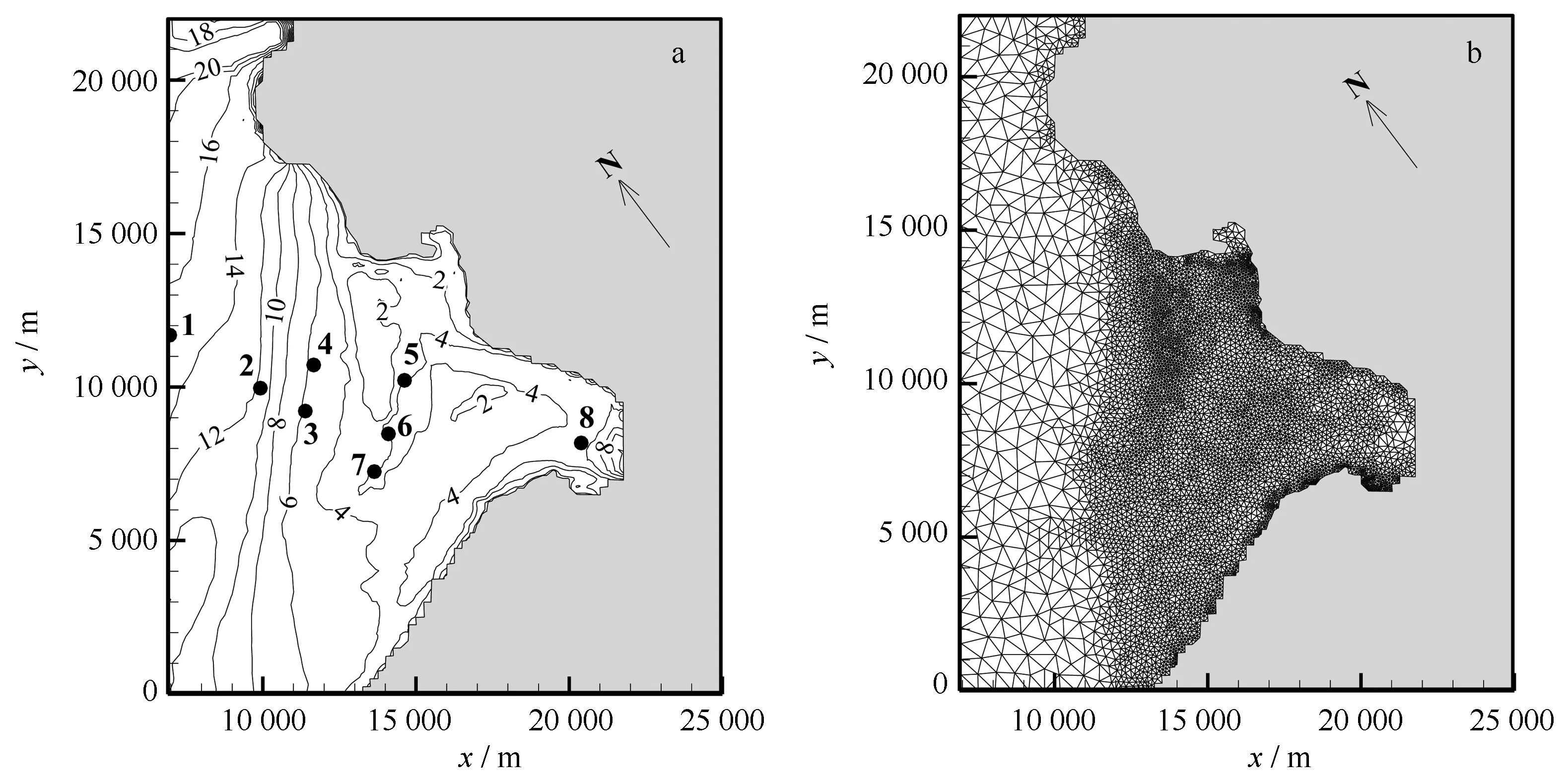
图2 实验区域地形(a)及网格分布(b)Fig.2 Bathymetry (a) and grid (b) of experimental area

图3 有效波高(a)与平均周期(b)的实测值和计算值比较Fig.3 Observed and computed significant wave height (a) and mean wave period (b)

3 结果与讨论

在实验区域内改变风速、风拖曳力系数计算方案和水深3个参数，利用SWAN模型进行敏感性实验，确定不同风速下各风拖曳力系数对波浪模拟的影响效果。

关于典型风速，首先选择与模型验证相同的风速，即14 m/s(以下简称V14)；其次选择FIT计算方案中风拖曳力系数达到最大值时对应的风速31.5 m/s(以下简称V31.5)；最后选择极端风速50 m/s(以下简称V50)，如图1所示，此时各计算方案间差别显著。以上所选风速可以分别代表一般大风、强热带风暴和强台风的极端条件。

由图2可知，大部分实验区域水深较小，波浪易发生破碎，可能出现在较高风速作用下无法达到其应产生的波高情况，从而无法真正体现不同风拖曳力系数对波浪模拟的影响效果。因此，这里除了考虑L1.7的情形之外，还包括将模型原水深统一增加10 m(以下简称L10)的条件，以减小波浪破碎的影响，此时实验区域的最大水深接近30 m。

表1给出了敏感性实验参数设置，其中L1.7V14WU对应上述模型验证部分。需要说明的是，除了L1.7V14WU，无法确定其他敏感性实验开边界处的真实波浪条件，为了保证参数改变的唯一性，这里均采用L1.7V14WU的波浪边界条件。

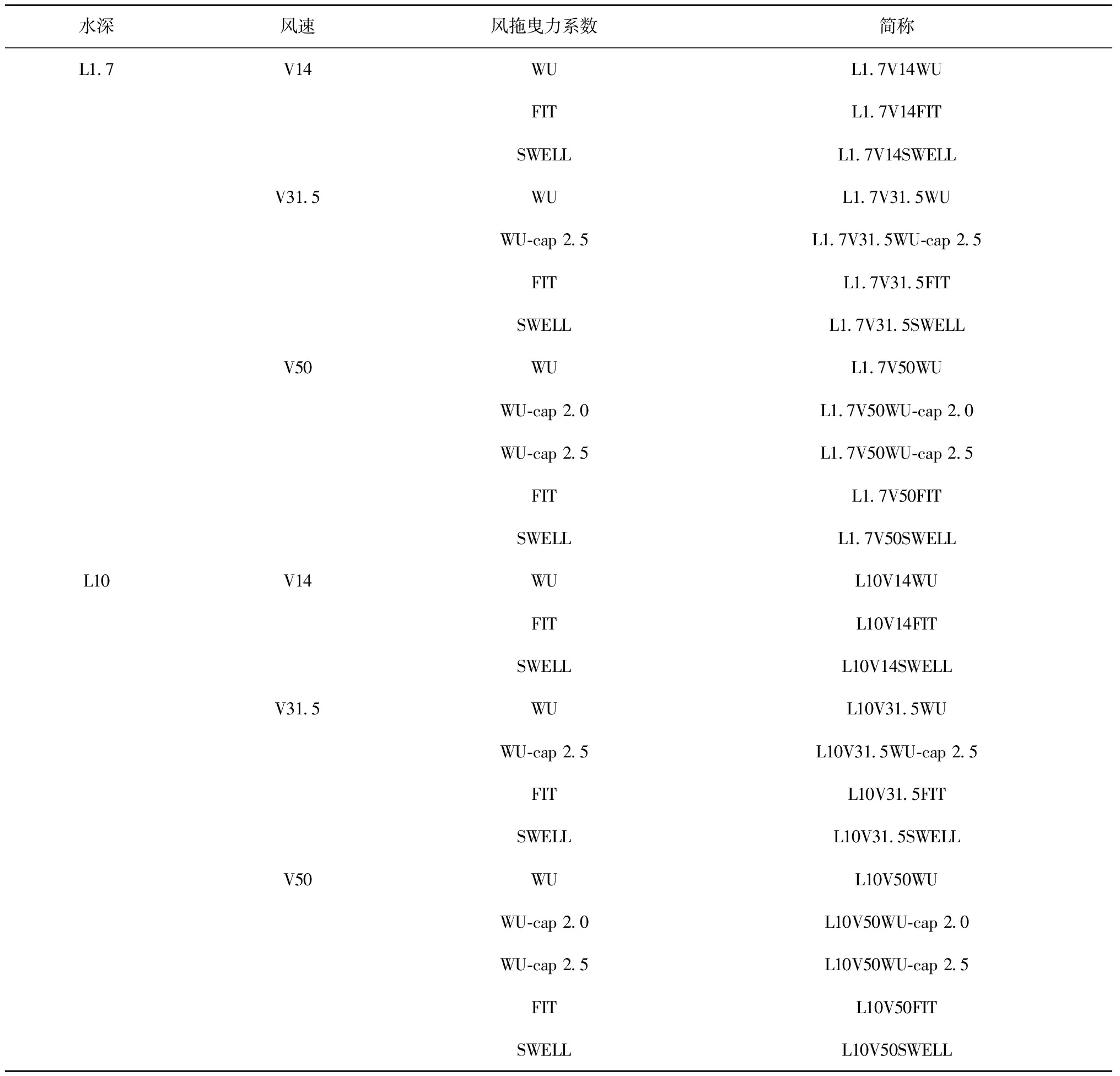
表1 敏感性实验参数设置

3.1 对有效波高的影响

在L1.7V14条件下，由图1可知，此时采用WU、WU-cap 2.0和WU-cap 2.5得到的风拖曳力系数是相等的，因此仅需比较WU、FIT和SWELL之间的差别，结果见图4a。由于风拖曳力系数相差很小，采用三者模拟的有效波高相差也很小。

在L1.7V31.5条件下，由于WU-cap 2.0和FIT得到的值非常接近，因此需要对WU、WU-cap 2.5、FIT和SWELL进行比较。图4c显示了相应的结果，四者差别仍然较小。同时随着风速的增大，各观测站处的有效波高除1号站受边界条件制约保持不变外，其余较L1.7V14均有所增大，特别是2号和8号站，其有效波高增大幅度均超过0.70 m。

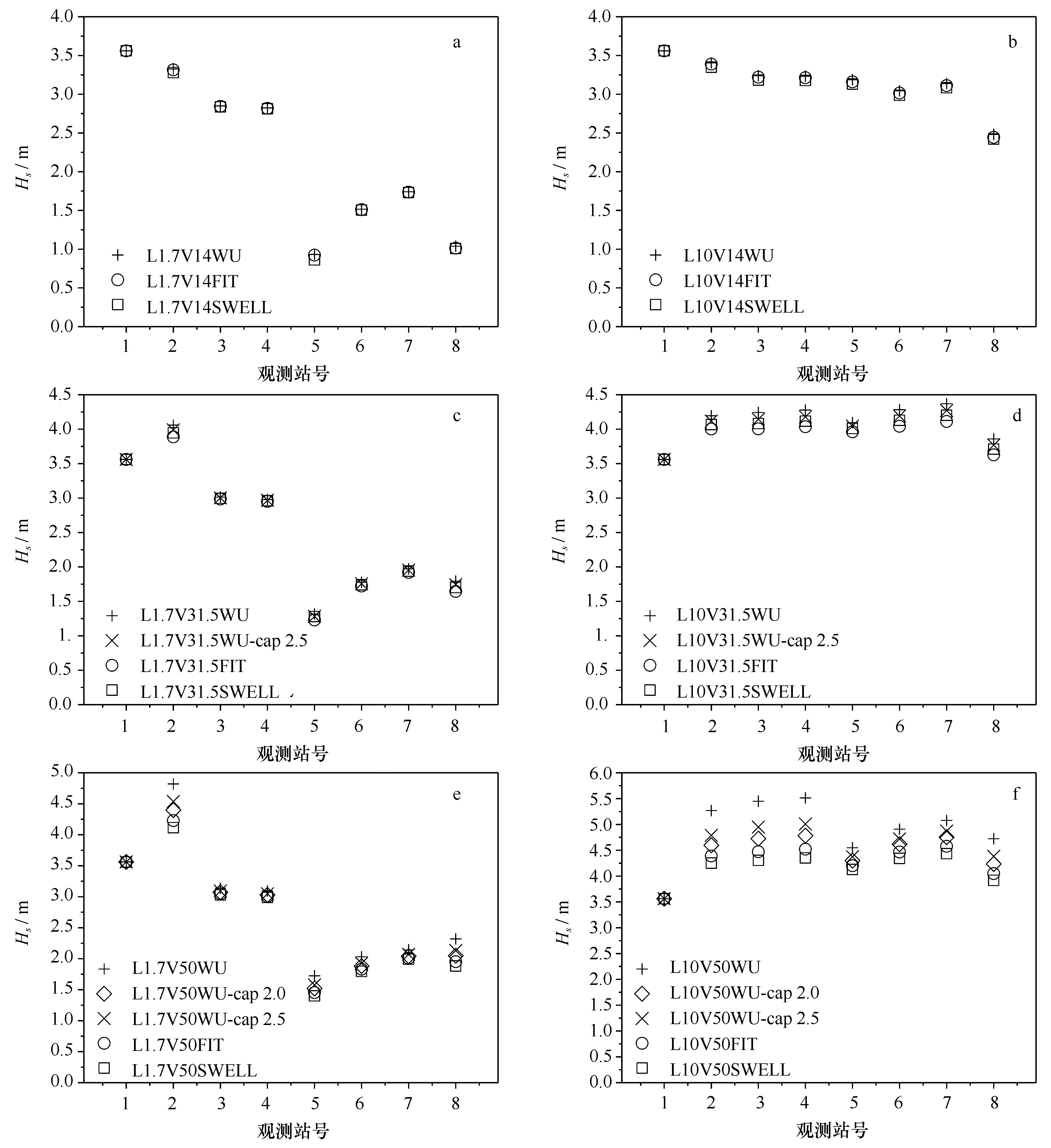
图4 敏感性实验中各观测站有效波高比较Fig.4 Significant wave height at observation stations in sensitivity experiments

在L1.7V50条件下，需要比较WU、WU-cap 2.0、WU-cap 2.5、FIT和SWELL的影响效果。如图4e所示，由以上五者计算得到的有效波高在2号、5号和8号站差别较为明显，其有效波高差值的最大值(WU和SWELL对应结果之差)分别为0.71 m、0.32 m和0.44 m。图5a和图5b分别给出了采用WU计算得到的实验区域有效波高及其与采用SWELL计算得到有效波高的差值分布，两者在水深较大处的差别在0.50 m以上，而在水深较浅处差别则降低至0.10 m左右，浅滩附近更是小于0.05 m。同时，与L1.7V31.5相比，如图4和图5c(以WU的结果为代表)所示，水深较浅处的各观测站有效波高变化较小，特别是浅滩附近的3号和4号站，其有效波高几乎未发生变化，这主要是水深变浅导致波浪破碎的结果。尽管风速值继续增大，但由于波浪破碎耗能的影响，在当地水深条件下不能产生与该风速对应的波高值，而只能是波浪破碎后的波高值。即当风速增加到一定程度后，波浪破碎成为影响波高值的主要因素。

图5 实验区域有效波高(m)及其差值(m)分布Fig.5 Distributions of significant wave height and (m) their difference (m) in experimental areaa.L1.7V50WU；b.L1.7V50WU-L1.7V50SWELL；c.L1.7V50WU-L1.7V31.5WUa.L1.7V50WU；b.L1.7V50WU-L1.7V50SWELL；c.L1.7V50WU-L1.7V31.5WU

水深统一增加后，在L10V14条件下，如图4b所示，SWAN模型采用各风拖曳力系数计算得到的有效波高都十分接近。与L1.7V14相比，除受边界条件影响的1号站外，其余观测站处的有效波高均有所增大，且5～8号站有效波高增大幅度大于2～4号站，特别是紧邻浅滩后侧的5号站，其有效波高增大超过2 m，说明水深增加10 m后，浅滩及波浪破碎的影响减弱。

在L10V31.5条件下，如图4d所示，同一观测站不同风拖曳力系数对应的有效波高的差异开始显现，有效波高差值的最大值为0.26 m。与L10V14对应结果相比，随着风速的增大，除1号站外，其余各观测站处有效波高均有所增大，且5～8号站的有效波高值与2～4号站有效波高的差距进一步缩小。

在L10V50条件下，如图4f所示，采用不同风拖曳力系数计算得到的有效波高差异增大，在部分观测站(2～4号站)采用WU和SWELL模拟得到的有效波高相差均超过1 m。图6a和图6b分别给出了采用WU计算得到的实验区域有效波高及其与采用SWELL计算得到有效波高的差值分布。与图5b相比，原水深较浅处经过加深后，波浪破碎的影响减弱，使得该部分区域有效波高差值大多显著提高至0.50 m以上，即使原浅滩位置的有效波高差异也增加至0.30 m左右。为了具体显示波浪破碎的影响区域，图6c给出了L10V50WU和L1.7V50WU条件下实验区域有效波高的差值分布。图中有效波高的差异向岸逐渐增大，结合图2a中试验区域的地形可见，10 m等深线以浅区域差别在0.5 m以上，原浅滩位置处更是超过3.0 m。综上所述，当采用SWAN模型计算台风风速量级以上风场作用下水深大于30 m的深水区域波浪场时，由于本文缺乏实验区域对应条件下的实测波浪资料，对于风拖曳力系数计算方案的选择，借鉴已有文献[16,19]研究结果，建议首先采用模型默认选项试算，然后结合当地海域实测波浪资料进行修正。

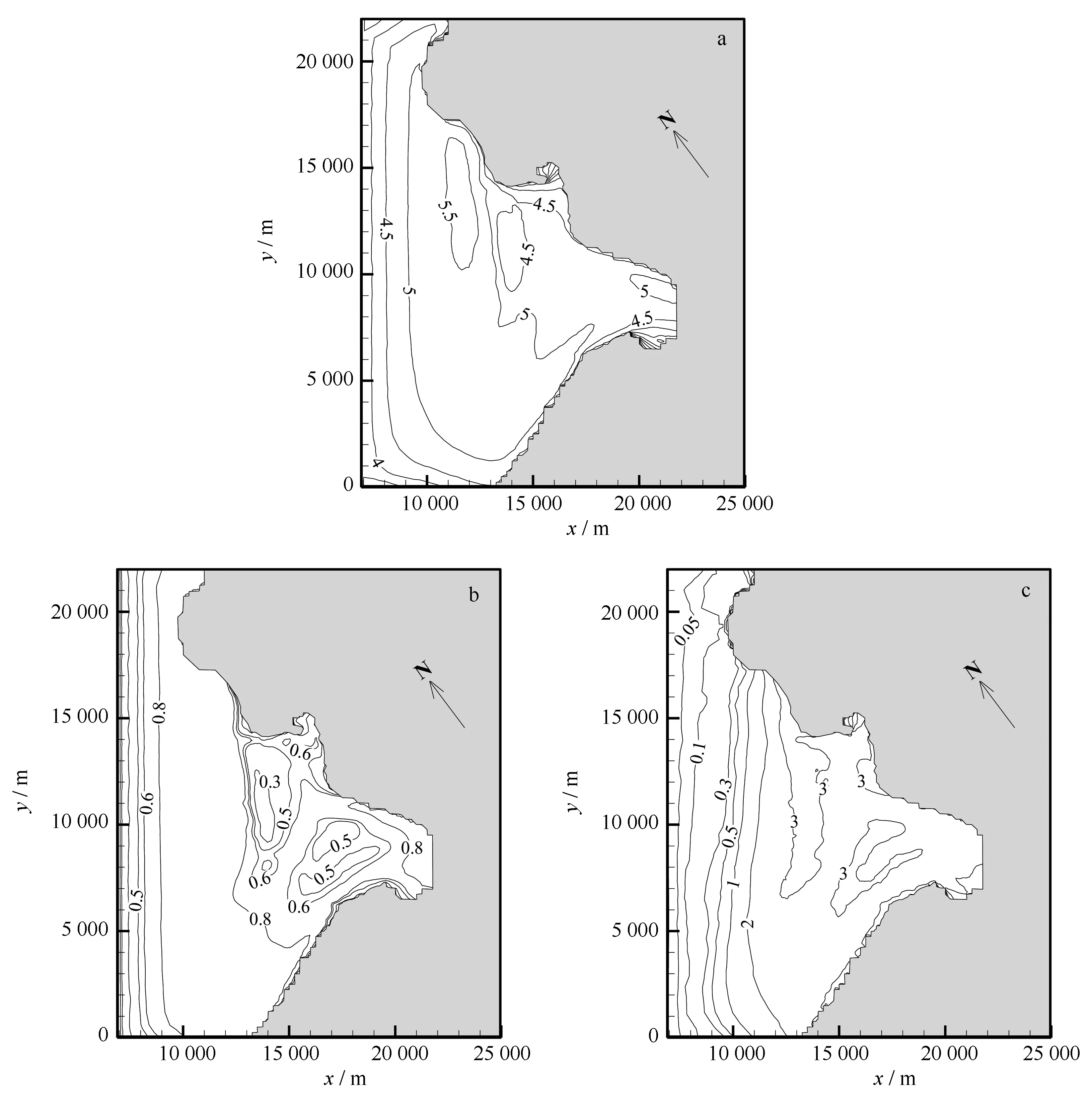
图6 实验区域有效波高(m)及其差值(m)分布Fig.6 Distributions of significant wave height (m) and their difference (m) in experimental areaa.L10V50WU；b.L10V50WU-L10V50SWELL；c.L10V50WU-L1.7V50WUa.L10V50WU；b.L10V50WU-L10V50SWELL；c.L10V50WU-L1.7V50WU

3.2 对平均周期的影响

在上文分析不同风拖曳力系数对有效波高影响基础上，这里将就其对平均周期的影响进行讨论。图7显示了L1.7V50和L10V50条件下各观测站平均周期的比较。从中可见，在同一水深下，各观测站处的平均周期对风拖曳力系数计算方案的选择并不敏感。水深增加后，即由L1.7变为L10，平均周期对风拖曳力系数计算方案的选择仍不敏感。需要说明的是，L1.7V14、L10V14、L1.7V31.5和L10V31.5条件下平均周期的变化情况与之类似，这里不再赘述。同时，在同一风拖曳力系数计算方案和风速条件下，随着水深的增加，原水深较浅处的平均周期相应增大，特别是5号站，平均周期的增加值超过3 s。图8a和图8b分别给出了L1.7V50WU和L10V50WU条件下实验区域平均周期分布。在实验区域天然水深条件下，如图8a所示，波浪的平均周期由水深较大处向水深较小处传播过程中逐渐减小，由水深变浅导致的波浪破碎对平均周期的影响较为显著。随着实验区域水深的统一增大，如图8b所示，波浪破碎的影响减小，各处的平均周期则趋于一致。

图7 敏感性实验中各观测站平均周期比较Fig.7 Mean wave period at observation stations in sensitivity experiments

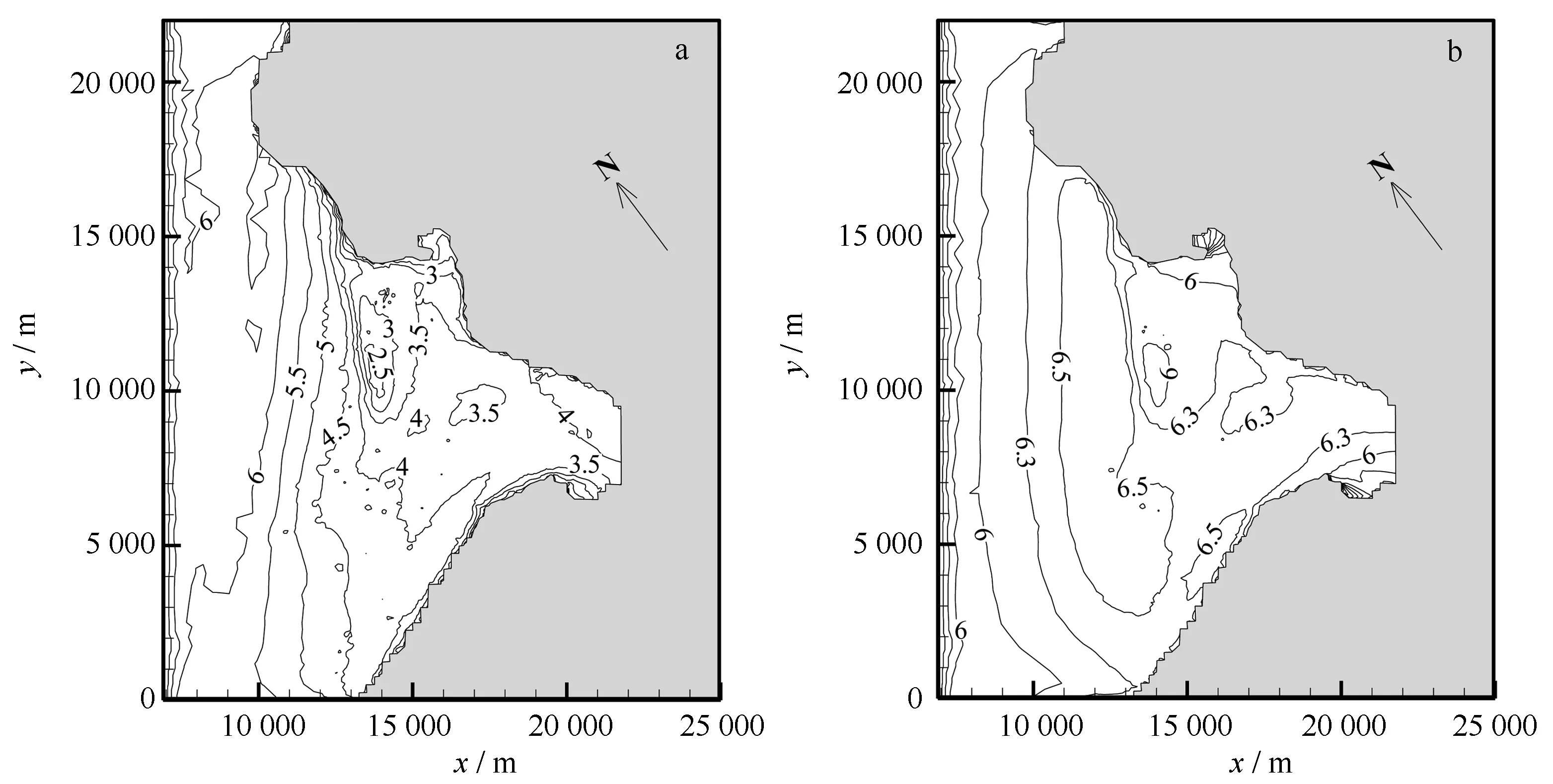
图8 实验区域平均周期(s)分布(a.L1.7V50WU；b.L10V50WU)Fig.8 Distributions of mean wave period (s) in experimental area(a.L1.7V50WU；b.L10V50WU)

4 结论

本文采用SWAN模型，选取模型中WU、WU-cap 2.0、WU-cap 2.5、FIT和SWELL 5个风拖曳力系数计算方案，以荷兰哈灵水道海域作为实验区域进行敏感性实验，研究在14 m/s、31.5 m/s、50 m/s的定常风速下各风拖曳力系数对波浪模拟的影响效果。本文从对有效波高和平均周期的影响两个方面进行分析，得到如下结论：

(1)对于近岸浅水区域(水深小于20 m)，风拖曳力系数计算方案的选择对有效波高影响较小，而且当风速增加到一定程度后，波浪破碎成为影响波高值的主要因素；对于深水区域(水深大于30 m)，一般大风条件下风拖曳力系数计算方案的选择对有效波高影响仍然较小，随着风速的继续增大，风拖曳力系数计算方案的选择对有效波高的影响逐渐显著。

(2)风拖曳力系数计算方案的选择和风速的改变对平均周期影响均较小，而由水深变浅导致的波浪破碎对其影响较为显著。

根据以上敏感性实验结果，本文建议使用SWAN模型计算近岸浅水区域风浪场或深水区域一般大风条件风浪场时，其风拖曳力系数可以直接采用模型默认选项；而对于深水区域更大风速条件，可首先采用模型默认选项试算，然后结合当地海域实测波浪资料进行修正。因此，当采用SWAN模型自嵌套方式模拟风浪从深水向浅水传播过程时，可首先确定外层模型在深水风浪计算时采用的风拖曳力系数计算方案，之后的内层模型可沿用外层模型的选择。

[1] 徐福敏, 张长宽, 陶建峰. 浅水波浪数值模型SWAN的原理及应用综述[J]. 水科学进展, 2004, 15(4):538-542.

Xu Fumin, Zhang Changkuan, Tao Jianfeng. Mechanism and application of a third generation wave model SWAN for shallow water[J]. Advances in Water Science, 2004, 15(4):538-542.

[2] 杨德周, 尹宝树, 徐艳青, 等. SWAN浅水波浪模式在渤海的应用研究——Phillips线性增长比例系数的改进[J]. 水科学进展, 2005, 16(5):710-714.

Yang Dezhou, Yin Baoshu, Xu Yanqing, et al. Application of the SWAN wave model to Bohai Sea: Improvement of Phillips linear growth term[J]. Advances in Water Science, 2005, 16(5):710-714.

[3] 夏波, 张庆河, 杨华. 水动力时空变化对近岸风浪演化的影响——以渤海湾西南岸为例[J]. 海洋通报, 2006, 25(5):1-8.

Xia Bo, Zhang Qinghe, Yang Hua. Influence of hydrodynamic factors on nearshore wind waves—the southwest coast of the Bohai Bay as an example[J]. Marine Scicence Bulletin, 2006, 25(5):1-8.

[4] 贾晓, 潘军宁, Niclasen B. SWAN模型风能输入项的改进与验证[J]. 河海大学学报, 2010, 38(5):585-591.

Jia Xiao, Pan Junning, Niclasen B. Improvement and validation of wind energy input in SWAN model[J]. Journal of Hohai University, 2010, 38(5):585-591.

[5] 宋伟伟, 陈国平, 严士常, 等. 基于台风浪后报模型的外海重现期波浪要素分析[J]. 水运工程, 2013(1):51-54.

Song Weiwei, Chen Guoping, Yan Shichang, et al. Wave parameters analysis of different return period in the open sea with a hindcast model of typhoon waves[J]. Port & Waterway Engineering, 2013(1):51-54.

[6] 罗蒋梅, 潘静, 杨支中. 海面风应力拖曳系数参数化方案对风暴潮数值模拟的影响[J]. 海洋预报, 2011, 28(3):15-19.

Luo Jiangmei, Pan Jing, Yang Zhizhong. Impact of the parameterization scheme about sea surface wind stress drag coefficients on numerical simulation of strom surge[J]. Marine Forcasts, 2011, 28(3):15-19.

[7] Garratt J R. Review of drag coefficients over oceans and continents[J]. Monthly Weather Review, 1977, 105:915-929.

[8] Large W G, Pond S. Open ocean momentum flux measurements in moderate to strong winds[J]. Journal of Physical Oceanography, 1981, 11(3):324-336.

[9] Wu J. Wind-stress coefficients over sea surface from breeze to hurricane[J]. Journal of Geophysical Research, 1982, 87(C12):9704-9706.

[10] Jarosz E, Mitchell D A, Wang D W, et al. Bottom-up determination of air-sea momentum exchange under a major tropical cyclone[J]. Science, 2007, 315(5819):1707-1709.

[11] Peng S, Li Y. A parabolic model of drag coefficient for storm surge simulation in the South China Sea[J]. Scientific Reports, 2015, 5:1-6.

[12] Weisberg R H, Zheng L. Hurricane storm surge simulations comparing three-dimensional with two-dimensional formulations based on an Ivan-like storm over the Tampa Bay, Florida region[J]. Journal of Geophysical Research, 2008, 113(C12):C12001.

[13] Oey L Y, Ezer T, Wang D P, et al. Loop current warming by Hurricane Wilma[J]. Geophysical Research Letters, 2006, 33(8):L08613.

[14] Powell M D, Vickery P J, Reinhold T A. Reduced drag coefficient for high wind speeds in tropical cyclones[J]. Nature, 2003, 422(6929):279-283.

[15] Zhao Zhongkuo, Liu Chunhua, Li Qi, et al. Typhoon air-sea drag coefficient in coastal regions[J]. Journal of Geophysical Research, 2015, 120(2):716-727.

[16] Zijlema M, van Vledder G P, Holthuijsen L H. Bottom friction and wind drag for wave models[J]. Coastal Engineering, 2012, 65:19-26.

[17] Holthuijsen L H, Powell M D, Pietrzak J D. Wind and waves in extreme hurricanes[J]. Journal of Geophysical Research, 2012, 117(C9):C09003.

[18] The SWAN team. SWAN user manual[D]. Delft: Delft University of Technology, 2016.

[19] Huang Y, Weisberg R H, Zheng L, et al. Gulf of Mexico hurricane wave simulations using SWAN: Bulk formula-based drag coefficient sensitivity for Hurricane Ike[J]. Journal of Geophysical Research, 2013, 118(8):3916-3938.

[20] Ris R C, Holthuijsen L H, Booij N. A third-generation wave model for coastal regions 2. Verification[J]. Journal of Geophysical Research, 1999, 104(C4):7667-7681.

Impact of wind drag coefficients on wave simulation using SWAN model

Ding Lei1，2, Yu Bo1

(1.CollegeofMarineandEnvironmentalSciences,TianjinUniversityofScience&Technology,Tianjin300457,China；2.TianjinMarineEnvironmentalProtectionandRestorationTechnologyEngineeringCenter,Tianjing300457,China)

Impact of wind drag coefficients in SWAN model on wave simulation was studied in the paper. Sensitivity experiments were conducted under wind speed 14 m/s, 31.5 m/s and 50 m/s (representing the conditions of strong wind, strong tropical storm and strong typhoon, respectively). Haringvliet in Holland was chosen as experimental area. Results show that in shallow water (shallower than 20 m), the wind drag coefficient has little effect on significant wave height. When the wind speed reaches a certain speed, wave breaking becomes a major factor affecting the significant wave height. In deep water (deeper than 30 m), the effect of wind drag coefficients on significant wave height is still small in condition of strong wind. As the wind speed increases further, the influence of wind drag coefficients on significant wave height becomes obvious gradually. The wind drag coefficient and wind speed have little influence on mean wave period whereas the wave breaking affects it significantly. According to the results of sensitivity experiments, choice of wind drag coefficients in SWAN model is suggested as follows. When the wind waves in shallow water are simulated, the default wind drag coefficient in SWAN can be directly used. As for deep water case, the default wind drag coefficient can be applied in condition of strong wind. When the wind speed is higher, the default wind drag coefficient can be tested firstly, and then it can be modified in terms of the field data if needed.

wind drag coefficient; SWAN model; wave simulation; significant wave height; mean wave period

P731.22

A

0253-4193(2017)11-0014-10

丁磊,于博. SWAN模型中不同风拖曳力系数对风浪模拟的影响[J]. 海洋学报, 2017, 39(11):14-23,

10.3969/j.issn.0253-4193.2017.11.002

Ding Lei, Yu Bo. Impact of wind drag coefficients on wave simulation using SWAN model[J]. Haiyang Xuebao, 2017, 39(11):14-23, doi:10.3969/j.issn.0253-4193.2017.11.002

2016-11-08；

2017-03-14。

国家自然科学基金项目(41276016)；国家科技支撑计划资助项目(2010BAC68B04)；天津科技大学科学研究基金资助项目(20130113)。

丁磊(1983—)，男，天津市人，博士，主要从事近海水动力及泥沙运动规律研究。E-mail：leiding2012@tust.edu.cn