“境趣共生”，帮助学生走向思维的远方

江苏如皋市白蒲小学 郭建军

“境趣共生”，帮助学生走向思维的远方

江苏如皋市白蒲小学 郭建军

数学课堂是一个愉悦、和谐的情感场，也是师生智慧碰撞的思维竞技场。数学活动在充满趣味的情境中，历经独立解答—交流分享—质疑互补—总结反思四个过程。数学课堂中的教师，应始终以同伴或朋友的身份与学生共同成长，引导学生不断地发现问题、提出问题、分析问题，进而能轻松地解决问题，帮助学生走向思维的远方。

境趣共生 独立解答 交流分享 质疑互补

曾有心理学家指出：小学生思维的基本特点是从以具体形象思维为主要形式逐步过渡到以抽象逻辑思维为主要形式。这种抽象逻辑思维在很大程度上，仍然是直接与学生的感性经验相联系的，具有很大成分的具体形象性。

本次的活动课上，留给学生们的一道题是近日引起众多教师热议的关于“啤酒”的数学题。题目是这样的：啤酒2元1瓶，两个空瓶可以换一瓶啤酒，四个瓶盖也可以换一瓶啤酒。现在有10元，最多能喝多少瓶？本节课的活动过程分四部分：独立解答—交流分享—质疑互补—总结反思。

一、独立思考后，交流分享

课前，充分了解学生，在尊重学生学习兴趣和认知出发点的基础上，将本题做成了店主和买家的一个对话情境，让各组成员根据情境，自己先独立审题，每个人从不同的角度去分析。独立思考之后，每一个学生都会有自己个性的发现，在小组交流分享环节中，让学生在小组内先发表自己的意见，把不能达成一致的观点都保留着，留作全班反馈时，成员之间进行质疑，再相互补充。笔者在此列举两个小组的交流片段。

[奋斗组]

奋斗组里有两种不同的意见，小文同学认为能喝15瓶，小米同学认为能喝20瓶。

小文用语言描述：10元钱可以买5瓶酒，（1）喝完5瓶酒，会有5个酒瓶和5个瓶盖，用其中的4个瓶盖子换1瓶酒，4个酒瓶换2瓶酒；还剩下1个瓶盖加上1个酒瓶；（2）喝完3瓶酒，会有3个瓶盖和3个酒瓶，加上前面剩下的1个瓶盖和1个酒瓶，就是4个瓶盖和4个酒瓶。4个瓶盖换1瓶酒，4个酒瓶换2瓶酒；（3）喝完3瓶酒，还剩下3个瓶盖和3个酒瓶，2个酒瓶换1瓶酒，喝完1瓶酒，会有1个酒瓶和一个瓶盖，3个瓶盖+1个酒瓶+1个瓶盖+1个酒瓶=4个瓶盖+2个酒瓶，4个瓶盖换1瓶酒，2个酒瓶换1瓶酒；（4）喝完2瓶酒，会有2个瓶盖和2个酒瓶，2个酒瓶换1瓶酒，喝完1瓶酒，剩下2个瓶盖+1个瓶盖+1个酒瓶=3个瓶盖+1个酒瓶。这样一共可以喝到：5+1+2+1+2+1+1+1+1=15（瓶），还剩下3个瓶盖和1个酒瓶没法换了。

小米同学则不认同只能喝15瓶，他的思路是这样的：前面和小文的思考是一样的，但还可以把她的解法继续，10元钱，在喝到15瓶酒以后，剩下1个酒瓶和3个瓶盖。再赊5瓶酒，喝完之后剩下5个酒瓶和5个瓶盖，再加上开始剩下的1个酒瓶和3个瓶盖，正好有6个酒瓶和8个瓶盖，正好是5瓶酒的金额。这样就可以喝上15+5=20（瓶）酒了。

[团结组]

团结组的小荟用画图的方式，呈现了这两种方法如下图：

（1）可以喝15瓶

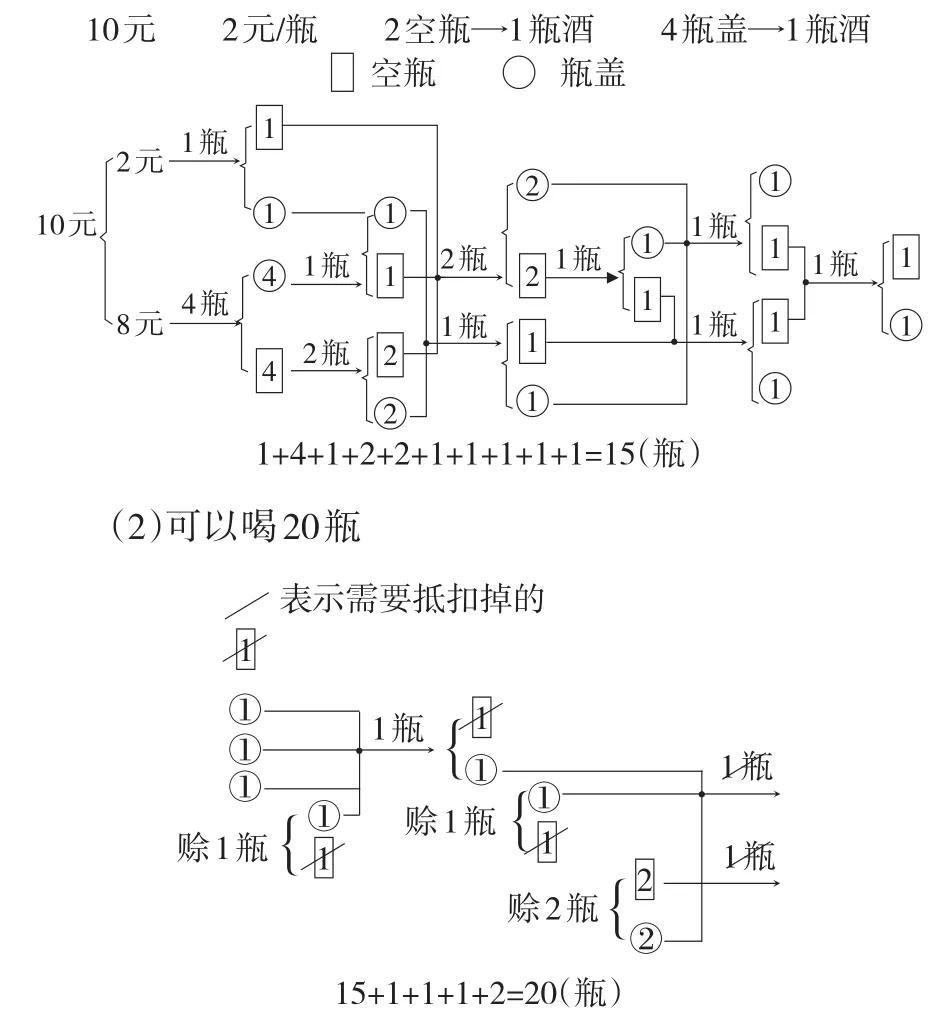
通过图示，小荟清晰地向全班描述着她的思路：“其实，这道题的答案我认为可以说成是‘最多喝15瓶’，也可以说成是‘最多喝16瓶’，也可以说成是‘最多喝17瓶’，也可以说成是‘最多喝18瓶’，也可以说成是‘最多喝19瓶’，也可以说成是‘最多喝20瓶’，这是在各种不同的情况下解出的答案。”原来大家已经几乎统一的答案又一下子被放开了，教室里再一次沸腾了，都期待着小荟把她放开的答案解释清楚。

二、拓展延伸后，总结反思

接着，讲台交给了小荟，同学们都静静地边看她的图示，边听她讲解着：“不管我们做出的哪一种答案，从15瓶到20瓶的答案，都可以进行解释。从图示上我们可以看出，在店主不允许赊账的情况下，我们最多只能喝15瓶，剩下的一个酒瓶和3个瓶盖不可以再换了；在允许赊账的情况下，我们还要看店主的情况，在图中看一看，他如果允许赊1瓶，那我们可以喝到16瓶，剩下4个瓶盖，再换一瓶，可以喝到17瓶，剩下1个酒瓶和一个瓶盖；如果他允许继续赊下去，我们可以继续喝，他不允许赊了就停止，但最多我们可以喝到20瓶。”

学生们的思路打开了，不再拘泥于一种答案了。在大家认同的时候，又有学生用其他方法解答。努力组的小晓同学给出了这样的解题思路：根据“啤酒2元1瓶，两个空瓶可以换一瓶啤酒，四个瓶盖也可以换一瓶啤酒”这几条数学信息，可以知道，“1个空瓶为1元，1个瓶盖为0.5元”，这样推算一下，一份纯啤酒就是0.5元了，题中要求最多能喝多少瓶啤酒？其实就是要计算出能喝多少份纯啤酒？用10÷0.5=20（瓶）就可以直接计算出可以喝到20瓶啤酒了。一直学习奥数的小丁同学，给出了这样的方程组：设一瓶酒的价值是x元，一个酒瓶的价值y元，瓶盖的价值z元。根据题意可以列出：x+y+ z=2，2y=2，4z=2，解得x=0.5，y=1，z=0.5，10÷0.5=20，最多可喝20瓶啤酒。

在现实生活中，我们很清楚地知道十块钱不可能喝到二十瓶酒。两个空瓶或四个瓶盖也不可能换到一瓶酒，要在这种特定的情境中，才存在这样的数学问题。在笔者看来，数学课堂应该是一个愉悦、和谐的情感场，也是学生们智慧碰撞的思维竞技场。课堂的每一分钟学生们都在享受着学习的过程。数学课堂中的教师，应当始终以同伴或朋友的身份与学生共同成长，引导学生不断地发现问题、提出问题、分析问题，进而能轻松地解决问题，帮助学生走向思维的远方。

1.注重独立思考，合作交流

曾有古人说：“独学无友，则孤陋寡闻。”因此，当下的合作学习能最大限度地促进学生们彼此间的成长。在本节数学活动课中，第一环节的独立思考之后的交流分享，学生先根据自己的思考，在自己的小组内相互讨论交流，探索出不同的解题思路和方法。在这一过程中，小组内进行激烈的争论，一方要说服另一方，组内成员的发言可以激起其他同学产生广泛的联想，通过互相补充、互相提示，学生的思维产生了碰撞，激发了彼此对数学内容的深化理解，同时思维得到了扩展，达成了小组内的暂时协同，无法统一的说法，留作第二环节中的全班同学质疑互补。

每个小组的代表在对其他同学的思路进行分析思考，做出自己的判断的过程中，自己对数学的理解更加丰富、全面。在相互沟通、相互质疑的过程中，学生不仅掌握了知识，合作能力、思维能力也得到了提高。

2.关注策略多样，结果开放

呈现在学生面前的数学问题，要能留给他们足够的思维空间，解决问题的方法、答案不要是唯一的，要具备开放性和多样性，让不同的学生在研究的过程中有不同的收获。每一个学生在研究中都有自己个性的想法，也会在与其他同学交流的过程中产生新的思考，如在解决“啤酒”问题的过程中，学生们进行了多元化的思考和表达，团结组的小荟运用简单的符号帮助自己进行分析，奋斗组的小文运用简单的文字描述进行记录，小米运用了假设的策略，其他同学运用了画图策略，无论运用什么方法解决问题。答案的得出并不唯一，正如团结组的小荟所说，“不管我们做出的哪一种答案，从15瓶到20瓶的答案，都可以进行解释……”本题重在培养学生们思考的多样性，也许有些学生对数学的理解是不太成熟的，但他们的理解往往都是个性的，合乎常理的。我们就是要珍视这些个性的资源，创造机会鼓励他们用自己的方式表达他们对题意的理解，引导他们用不同的策略解题，加深他们对数学的理解。

在数学教学过程中,学生思维能力的激发与培养尤为重要。在基于学生的经验、学生自身高度的基础上，教师应巧妙设计利于学生思维发展的趣味性的探索问题，引导他们不断超越自己，不断获得新的进步、新的成长，感受数学思维的美，从而催生数学学习的真正发生。