基于随机共振理论对2FSK信号输出误码率的研究
王 硕,王辅忠,尚金红,张光璐
(天津工业大学 理学院,天津 300387)
基于随机共振理论对2FSK信号输出误码率的研究
王 硕,王辅忠,尚金红,张光璐
(天津工业大学 理学院,天津 300387)
2FSK信号常用于进行中低速数据传输,但在强噪声背景下2FSK信号接收产生的误码率较高,基于以上问题提出了一种基于随机共振理论降低2FSK信号相干接收误码率的新方法。根据随机共振原理建立了非线性系统模型,进行数值实验研究,并与传统降低误码率的解调方法进行对比。实验数据显示,系统输入信噪比在-14.3~0 dB时,输出的误码率会呈现大幅度的降低,其中系统输入信噪比在-6.5 dB时,相比于传统模型误码率下降了14.3%,同时输出的频谱载波幅值是传统方法的2.07倍,系统输出信号的准确率得到大幅提升。
随机共振; 误码率; 2FSK信号; 非线性双稳系统; 信噪比
数字信号在传输过程中,衰变改变了信号的电压, 致使信号在传输中遭到破坏,产生误码[1],较高的误码率会影响信号传送的准确性。传统的解调方法是通过采用差错控制技术或最佳匹配滤波器等方法减小系统输出的误码率。例如:加入差错控制编码的正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)系统[2],当系统输入信噪比在10~15 dB时,系统输出误码率可以控制在10-3以内,达到比较理想的信号质量。但是传统方法对系统的输出环境要求较高,一般要在信噪比大于0 dB的环境下误码率才会有明显的降低,在信噪比小于0 dB的强噪声环境下,系统输出的误码率仍然维持在一个较高的水平上。
1981年,为了解释第四冰川世纪问题,Benzi等[3]提出了随机共振(Stochastic Resonance, SR)的概念。该概念的提出为在强噪声条件下的信号检测提供了一种新思路,克服了传统方法中将噪声作为干扰项的局限性。随后随机共振在应用方面研究引起了人们的普遍关注,从国内外的研究结果可以看到,随机共振在疾病的治疗[4]、语音信号处理[5]、神经网络[6]等各个方面都有很大的研究进展。但以上的研究内容大多集中在模拟信号领域,而随机共振理论在数字信号处理领域的研究还较少。
2FSK(Binary Frequency-Shift Keying)信号利用载波频率传送数字信号,符号“1”对应载频,符号“0”对应载频的已调波形[7],他们之间的改变是瞬间完成的。相比较于2ASK、2PSK信号,2FSK信号转换速度快、波形好、稳定度高、抗噪声与抗衰减性能较好且易于实现[8],使其在中低速数据传输中得到了最早而且也是最广泛的应用。本文选取2FSK信号,利用随机共振理论[9],分析在输入信噪比小于0 dB的强噪声条件下,随机共振系统对系统输出误码率的影响,并在时域、频域、系统输出误码率三个方面分析研究了随机共振方法相较于传统方法的优势。
1 2FSK信号随机共振模型及原理
非线性双稳系统的动力学方程可用Langevin 方程[10-12]表示
dx/dt=ax(t)-bx3(t)+s(t)+n(t)
(1)
式中:a、b为非线性双稳系数,通常取a=1,b=1;n(t)是强度为D的加性高斯白噪声;s(t)为2FSK信号,振幅为A。在一个码元的持续时间Ts内,发送端产生的2FSK信号可表示为
(2)
其中,
(3)
(4)
取信道传输系数为K,令α=AK,在(0,Ts)时间内,接收端的输入合成波形yi(t)为
(5)
即
(6)
2FSK信号传统同步检测法系统[13]和随进共振法系统模型分别如图1(a)、图1(b)所示。
2 2FSK信号随机共振系统输出理论误码率
设信道输出信号的采样时间为Δt,并以其进行一阶保持采样,则Δt时间内信号和噪声可表示为

(a) 同步检测法系统模型

(b) 随机共振法系统模型图1 2FSK信号接收模型Fig.1 The 2FSK signal’s reception model si(nΔt)+ni(nΔt),i=1,2,…,n=1,2,…
(7)
代入式(1)得
dx/dt=ax(t)-bx3(t)+si(nΔt)+ni(nΔt),(n-1)Δt≤t (8) 在一个码元的时间间隔内,系统输出的信号在相干解调之后的采样值为常数,设其为S,则S=±A,代入式(8)中得 dx/dt=ax(t)-bx3(t)+S+ni(nΔt) (9) 将式(8)做以下变换 (10) 则 (11) 式(11)中ξ(t)为归一化后的噪声,〈ξ(t)ξ(0)〉=2δ(t),其噪声强度不发生变化,通过调节系统的参数可使系统发生随机共振现象。该式表征的非线性系统模型所输出的概率密度函数f(y,t)=ρ(y,t),此函数满足Fokker-Planck方程[14] ∂2ρ(y,t)/∂y2 (12) 上支路 (13) 下支路 (14) 其中, (15) (16) C0则由概率密度归一化条件所得到。 当x1(t)的抽样值x1 (17) (18) 同理可得,判决器应输出“0”错判为“1”的概率 (19) pe=p(1)p(0|1)+p(0)p(1|0) (20) 3.1时域、频域分析 将图1(a)、图1(b)两模型中分别输入幅度A=0.3,输入信噪比为-9 dB的信号,其中图1(b)模型输入经过我们前期研究结果[15]自适应系统得到的模型最佳参数a=0.6,b=0.69。 图2为两种模型分别输出的时域图。在图2(a)中传统模型输出的信号受到噪声的严重干扰,波形被噪声完全淹没;在图2(b)随机共振法系统模型中输出的信号时域图形成较为明显的近似周期信号。这表明2FSK信号和噪声信号在通过随机共振系统的过程中发生了随机共振现象,根据随机共振理论可知,信号通过随机共振系统时,部分噪声能量被信号吸收,从而使信号能量得到增强,消除了部分噪声对信号的干扰作用。 图3(a)、图3(b)显示了2FSK信号在分别通过图1(a)、图1(b)两种模型后输出的频谱图。图3(a)中2FSK信号的载波频谱幅峰值为10 183.41,图3(b)中2FSK信号的载波频谱幅峰值为21 148.29,由此看出随机共振非线性双稳态模型比传统模型输出的载波频谱幅峰值高2.07倍,说明随机共振非线性双稳态系统较传统模型可以更加准确的检测载波信号频率。 3.2误码率分析 利用MATLAB对图1中两种模型进行仿真模拟实验。载波信号频率fc=0.01 Hz,系统输入信噪比变化范围为-15~5 dB,由于信号在经过信道以后会产生一定程度的衰减,故在仿真模拟试验中,2FSK信号的幅度选择小于1的0.2、0.3、0.4、0.5四种幅度,选择500个码元进行数值实验,二进制基带信号码元周期T=100 s。 (a) 通过图1(a)模型的时域波形 (b) 通过图1(b)模型的时域波形图2 2FSK信号通过图1(a)、图1(b)模型的时域波形图Fig.2 The 2FSK signal’s time domain graph when it through the model of Fig.1(a) and Fig.1 (b) (a) 通过图1(a)模型的频谱图 (b) 通过图1(b)模型的频谱图图3 2FSK信号通过图1(a)、图1(b)模型的频谱图Fig.3 The 2FSK signal’s time spectrum graph when it through the model of Fig.1(a) and Fig.1 (b) 图4中分别显示出随机共振法系统模型的输出误码率和同步检测法系统模型的输出误码率曲线以及理论误码率曲线。从图4中可以看出传统模型的输出误码率曲线和理论误码率曲线十分相近,系统的误码率随着信噪比的增加而减小。当系统输入的信噪比在-15~-14.3 dB时,随机共振非线性系统输出的误码率明显小于传统系统的误码率,但是下降的幅度不大。当系统输入信噪比在-14.3~-6.9 dB时,随机共振法系统模型输出的误码率曲线斜率明显大于传统系统模型,误码率下降非常明显,此结果表明在强噪声背景下,利用随机共振方法接受2FSK信号获得信息的准确程度优于使用传统方法。在输入信噪比在-6.9~0 dB时,系统输出的误码率曲线下降幅度趋于平滑,当系统输入信噪比在0 dB附近时系统输出的误码率超过传统方式所输出的误码率。在输入信噪比大于0 dB之后,系统输出误码率曲线接近于直线,曲率基本保持不变,而传统模型的误码率仍在不断的减小,系统输出的误码率最终小于随机共振非线性双稳系统所输出的误码率。 (a) A=0.2 N=500 (b) A=0.3 N=500 (c) A=0.4 N=500 (d) A=0.5 N=500图4 随机共振非线性系统模型、传统模型输出误码率与理论值比较Fig.4 Comparison of output bit error rate between the stochastic resonance of nonlinear system and the traditional model 图5显示了在A=0.2、A=0.3、A=0.4、A=0.5四种不同情况下系统输出误码率的比较。由图5可知,当系统输入的信噪比在-15~-1.9 dB时,由于系统同时受到噪声与周期信号的共同影响,其中周期信号将随机共振双稳态系统势阱间切换引入周期性变化[16],从而有效的对噪声所引起的切换进行协调与同步,使输入信号与输出信号的频率达到相同。当系统输入的信噪比相同时,系统发生的随机共振所吸收的噪声能量随着信号幅度的减小而增加,从而推断出当系统发生随机共振现象越明显,系统所输出的误码率就越低。图5中在不同幅度条件下,通过模拟仿真实验得到的四条误码率曲线的变化趋势基本一致,可以说明图1(b)的随机共振系统稳定可靠性较高。 图5 不同信号幅值下的误码率变化曲线(f=0.01 Hz, N=500)Fig.5 Change of the bit error rate under different signal amplitude along with SNR (f=0.01 Hz,N=500) 本文基于随机共振原理建立了系统模型,实现了系统在输入2FSK信号时的随机共振现象。在系统输入信噪比为-15~5 dB时,通过时域、频域和系统输出误码三个方面与传统模型进行了对比研究,发现随机共振模型相较传统模型有着很大的优越性。实验数据显示:系统输入信噪比在-14.3~0 dB时,随机共振系统输出的误码率较传统同步检测法系统有大幅度的降低,其中系统输入信噪比在-6.5 dB时,相比于传统模型误码率下降了14.3%,同时输出的频谱载波幅值是传统方法的2.07倍,系统输出信号的准确率得到大幅提升。表明本文所提出的系统在强噪声背景下可以更加准确的检测出载波信号。 [1] 李宝国.探讨SDH光纤传输系统误码问题[J]. 工业B,2015 (9):158. LI Baoguo. Discusses the issue of SDH optical fiber transmission system error[J]. Industrial B, 2015 (9):158. [2] 李晶, 侯思祖.OFDM误码率性能分析与研究[J].微计算机信息, 2006, 22(3): 261-264. LI Jing, HOU Sizu. Analysis and study of performance of OFDM ber[J]. Microcomputer Information, 2006, 22(3):261-264. [3] BENZI R, PARISI G, STUEM A. A theory of stochastic resonance in climatic change[J]. SIAM Journal on Applied Mathematics, 1983, 43(3): 565-578. [4] 余毅震,史俊霞,吴汉荣.功能性磁共振成像在高级认知功能研究中的应用[J].中国社会医学杂志, 2006, 23(3): 153-156. YU Yizhen, SHI Junxia, WU Hanrong. Application of functional magnetic resonance imaging on the research of cognitive function[J]. Chinese Journal of Social Medicine,2006,23(3):153-156. [5] 刘磊,范铁生,王银斌,等.基于信号包络分析的并行微弱信号检测算法[J].计算机应用, 2012, 32(8): 2133-2136. LIU Lei, FAN Tiesheng, WANG Yinbin, et al.Parallel weak signal detection algorithm based on envelope analysis[J]. Journal of Computer Applications, 2012, 32(8): 2133-2136. [6] 于海涛,王江,刘晨,等.耦合小世界神经网络的随机共振[J].物理学报,2012,61(6):68702. YU Haitao,WANG Jiang,LIU Chen, et al.Stochastic resonance in coupled small-world neural networks[J].Acta Physica Sinica, 2012,61(6):68702. [7] 毛炜,金荣洪,李家强,等.基于HHT变换的时频分析法及其在2FSK系统解调中的应用[J].电子与信息学报,2006,28(12):2318-2322. MAO Wei, JIN Ronghong, LI Jiaqiang, et al.Time-frequency analysis method based on HHT and its application in 2FSK demodulation systems[J]. Journal of Electronics & Information Technology, 2006,28(12):2318-2322. [8] 毕红博.基于混沌振子FSK微弱信号检测方法的研究[D].河北:华北电力大学,2008. [9] HARI V N, ANAND G V, PREMKUMAR A B. Stochastic resonance phenomenon in an underdamped bistable system driven by weak asymmetric dichotomous noise[J].Signal Processing, 2012, 92: 1745-1757. [10] ZOU H L, ZHENG L Q, LIU C J. Detecting parameters of high frequency signals with frequency modulation stochastic resonance[C]∥2013 6th International Congress on Image and Signal Processing. [S.l.]: CISP, 2013: 1090-1095. [11] 夏均忠,刘远宏,马宗坡,等.基于调制随机共振的微弱信号检测研究[J].振动与冲击, 2012,31(3):132-135. XIA Junzhong, LIU Yuanhong, MA Zongpo, et al. Weak signal detection basing on modulated stochastic resonance[J]. Journal of Vibration and Shock, 2012, 31(3):132-135. [12] ZHANG G L, WANG F Z. Research of stochastic resonance in cascaded bistable system[J]. Journal of Computational and Theoretical Nanoscience, 2009, 6(3): 676-681. [13] 徐艺文,陈忠辉,李雷,等.基于DFT的2FSK信号解调自适应门限同步检测算法[J].四川大学学报(工程科学版),2011,43(1):169-173. XU Yiwen, CHEN Zhonghui, LI Lei, et al. Adaptive threshold synchronous-detection algorithm for 2FSK signal demodulation based on DFT[J]. Journal of Sichuan University( Engineering Science ), 2011,43(1):169-173. [14] RISKEN H. The fokker-planck equation[M]. New York:Springer, 1983: 63-65. [15] GAO Y, WANG F. Adaptive cascaded-bistable stochastic resonance system research and design[J]. Journal of Computational and Theoretical Nanoscience, 2013, 10(2): 318-322. [16] 陈敏,胡茑庆,秦国军,等.参数调节随机共振在机械系统早期故障检测中的应用[J].机械工程学报,2009,45(4):131-135. CHEN Min, HU Niaoqing, QIN Guojun, et al. Application of parameter-tuning stochastic resonance for detecting early mechanical faults[J]. Journal of Mechanical Engineering, 2009,45(4):131-135. 2FSKsignaloutputerror-rateinfluencedbyanonlinearstochasticresonancesystem WANG Shuo, WANG Fuzhong, SHANG Jinhong, ZHANG Guanglu (School of Science, Tianjin Polytechnic University, Tianjin 300387, China) 2FSK signals are often used for low speed data transmissions. But, in the case of strong noise, 2FSK signals may receive higher error rate. A novel method for decreasing the coherent reception error rate of binary phase shift keying signals based on the stochastic resonance theory was introduced to get the enhanced reception of 2FSK signals under noisy environment. The model was built in accordance with the stochastic resonance theory and put into use by utilizing MATLAB. Compared with the traditional demodulation, method, a great reduction in the signal to noise ratio(SNR) was obtained from -14.3-0 dB. The error rate is decreased by 14.3%. Meanwhile, the spectrum amplitude of the outputting carrier wave is 2.07 times that by using the previous method. stochastic resonance; bit error rate; 2FSK signal; nonlinear bistable system; signal to noise ratio O324; TN914.3 A 10.13465/j.cnki.jvs.2017.19.002 国家自然科学基金资助项目(61271011) 2016-05-13 修改稿收到日期:2016-07-19 王硕 男,硕士生,1989年生 王辅忠 男,教授,1960年生



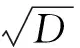
3 实验数据分析









4 结 论

