钢管束组合剪力墙变形性能研究及有限元分析

陈志华，姜玉挺，张晓萌，杨强跃，李文斌，胡立黎，李 杰

(1. 天津大学 水利工程仿真与安全国家重点实验室，天津 300072；2. 天津大学 建筑工程学院，天津 300072；3. 杭萧钢构股份有限公司，杭州 310003)

钢管束组合剪力墙变形性能研究及有限元分析

陈志华1,2，姜玉挺2，张晓萌2，杨强跃3，李文斌3，胡立黎3，李 杰2

(1. 天津大学 水利工程仿真与安全国家重点实验室，天津 300072；2. 天津大学 建筑工程学院，天津 300072；3. 杭萧钢构股份有限公司，杭州 310003)

提出一种新型钢板剪力墙结构-钢管束组合剪力墙。对7组钢管束组合剪力墙在往复荷载作用下的性能进行试验研究，分析其滞回曲线及骨架曲线，并对墙体变形能力及钢板应变性能进行了分析，研究墙体在不同阶段破坏形态。同时以该试验为基础，采用ABAQUS有限元软件分析钢管束组合剪力墙的力学性能。研究结果表明,钢管束组合剪力墙具有较高的承载力和良好的抗震性能，滞回曲线饱满。对不同钢管束截面，钢板厚度，剪跨比以及是否布置栓钉等参数进行了分析，对比其受力模式。通过试验现象、应力应变分析及有限元分析可以看出，试件最终破坏多为墙体下部出现钢板受压屈曲或受拉撕裂及混凝土压溃。

钢管束组合剪力墙；试验研究；变形分析；破坏形态；有限元分析

钢板-混凝土组合剪力墙与传统混凝土结构相比是一种承载力高、延性好、耗能能力强的新型墙体结构，组合剪力墙结构充分利用钢材和混凝土材料的特点，施工方便,相对经济，并且墙体厚度小，有效增加建筑使用空间，整体自重轻，减小结构整体自重，可以被广泛使用于高层结构住宅当中。目前组合钢板剪力墙主要分两种形式，内置钢板组合剪力墙及外包钢板-双钢板组合剪力墙。Wright等[1-2]对双压型钢板内填混凝土组合剪力墙的轴压和抗剪性能进行了研究，并提出相关的设计方法。吕西林等[3]，Zhao等[4]分别对内置钢板的剪力墙结构进行了抗震性能研究。Link等[5-6]对内设加劲肋的双钢板组合剪力墙开展了试验研究，验证了其良好的抗震性能。聂建国等[7-8]分别进行了多组双钢板混凝上组合剪力墙及外包多腔钢板-高强混凝土组合剪力墙上拟静力抗震性能试验，研究了该类结构的受力机理，及良好的延性和耗能能力，变形能力。纪晓东等[9]进行了一种钢管-双层钢板-混凝土组合剪力墙的实验研究，研究了其抗震性能，并提出承载力计算公式。

钢板剪力墙在目前的结构体系中，多作为抗侧力构件承担水平荷载，且大多钢板剪力墙因钢板厚度较厚，用钢量过高，很难广泛推广应用于普通高层建筑中，同时由于构造复杂、加工困难、造价偏高、难以实现装配化[10]。本文提出的钢管束组合剪力墙为采用薄壁钢管的新型剪力墙，将作为主要承重与抗侧力构件广泛用于高层建筑中，建筑结构体系主要由钢管束组合剪力墙与H型钢梁组成，其具有节省用钢量、施工方便快捷、装配化程度高、经济性能良好等一系列优点。对新型钢管束组合剪力墙进行了1∶1足尺模型的滞回性能试验研究[11]，研究了该种形式剪力墙的破坏机制、承载能力、滞回性能和变形特性，考察了不同轴压比、剪跨比、不同截面尺寸的U型钢以及是否布置栓钉等参数对剪力墙受力性能的影响。以7组钢管束组合剪力墙试验为基础，建立了有限元模型，与试验结果进行了对比分析。

1 试验概况

1.1试验设计

试验设计了7个钢管束组合剪力墙足尺模型,编号为YZQ1-YZQ7。按照实际工程1∶1足尺试件进行研究，墙体高度为2 700 mm，长度由 1 324～1 924 mm，宽度130 mm，剪跨比由1.51～2.09。钢管束组合剪力墙由120 mm×130 mm，160 mm×130 mm，200 mm×130 mm等不同截面U型钢连接而成，连接方式为焊接，内填混凝土。

其典型截面如图1所示，所有的试件均采用相同材料的钢材和混凝土，试验主要变化参数为轴压比、U型钢长度和厚度、钢板剪力墙长度以及是否布置栓钉。试件1～试件7的基本构造一样，为U型钢通过对接焊接连接而成，中心处由一块钢板焊接连接，U型钢中间填充混凝土，U型钢侧面开45 mm×80 mm椭圆孔，方便每个U型钢之间的混凝土流通。墙体钢板通过等强熔透焊与60 mm厚的底板及40 mm厚的顶板连接，为了防止焊缝在试验过程中出现破坏，剪力墙底部周圈焊一圈50 mm高4 mm厚的钢板，增强连接性能，在试件顶部及底部分别设置基础梁及加载梁，底板及顶板通过足够的高强螺栓与基础梁和加载梁相连，主要设计参数见表1。

表1 各试件参数Tab.1 Parameters of test specimens

1.2材料性能

试件浇筑的同时,制作6块150 mm×150 mm×150 mm立方体试块，并与试件同条件养护，试验当天进行测试，得到实测混凝土立方体抗压强度:fcu=47.11 MPa。钢板依照GB/T 228—2002《金属材料室温拉伸试验方法》的规定取样加工，量测其屈服强度fy，抗拉强度fu。钢材材性3 mm钢板屈服强度424 MPa极限强度498 MPa；4 mm钢板屈服强度433 MPa极限强度504 MPa；5 mm钢板屈服强度419 MPa极限强度538 MPa。以上材料强度值均为各试件强度平均值。

1.3实验装置及加载方式

加载装置采用20 000 kN重型结构多功能空间加载装置。该装置竖向加载能力20 000 kN，水平加载能力3 500 kN，竖向荷载通过竖向千斤顶施加，水平荷载通过两个液压伺服加载装置施加。基础梁通过锚梁、地锚螺栓锚固于试验台座。加载梁通过丝杠、端板与水平千斤顶端面相连。试件顶部放置加载梁，将千斤顶轴压力均匀传到端柱和中间墙体,加载装置如图2所示。

试验时先按轴压比的要求施加竖向荷载，保持恒定。然后进行水平低周反复加载。水平荷载加载过程采用力-位移混合控制法：试件在弹性阶段按照力控制分为3级加载，每级荷载循环一次，当到达预测的屈服荷载后进行位移控制。屈服后采用位移逐级加载，构件1、构件2以屈服荷载的1倍位移加载，每级荷载循环两次；其余构件以屈服荷载的0.5倍位移加载，每级荷载循环两次。当试件不能维持施加的轴压力或水平力下降到峰值水平力的85%以下时，停止实验[12-13]。

(a)YZQ1、YZQ2立面图(b)1-1剖面图

(c) YZQ1、YZQ2横截面图图1 试件YZQ1、YZQ2几何尺寸及构造详图Fig.1 Demensions and details of YZQ1 and YZQ2

图2 加载装置Fig.2 Test setup

1.4测点布置及量测方案

试验中的量测的主要内容包括试件的竖向荷载、水平荷载，水平位移，相对变形和应变等。YZQ1测点布置如图3所示。顶部加载梁截面中心布置位移计H-1；沿墙体侧面布置位移计H-2～H-4，测量墙端的水平位移；在基础梁上布置 1个水平位移计H-5 和2个竖向位移计V-1、V-2，用以修正基础梁平动、转动对试件位移值的影响；交叉布置位移计H-8、H-9测量试件的剪切变形。此外，在试件中布置20个应变片、20个应变花，用以考察墙体塑性发展规律。测量数据通过电脑自动记录,通过细致的观察和拍照 录像来记录钢板的屈曲、变形和破坏。其余墙体除对个别应变片适当调整，测点及位移计布置与YZQ1基本相同。

(a)(b)

2 试验现象及分析

2.1破坏过程与破坏形态

YZQ1～YZQ7破坏模式及现象大体相同，根据试验现象分析，可将各试件受力全过程分为三个阶段。

(a) 弹性工作阶段

开始加载时，试件无明显的现象，加载过程中出现轻微响声，各试件水平荷载-位移曲线基本呈线性变化，墙体没有任何屈曲现象发生。

(b) 屈服阶段

弹性工作阶段后，试件水平荷载位移曲线出现转折点，位移角到1/150～1/108时，墙体两侧钢管束底部150～200 mm开始出现轻微屈曲，随着水平荷载的增加，屈曲现象出现的区域开始增加，并且更为明显，到达峰值荷载时，受压区角部边起前3根钢管束150～300 mm高度会出现较明显屈曲；敲击钢板，出现明显空响声，表示钢板与混凝土脱离。

(c) 破坏阶段

荷载到达峰值荷载之后，随着位移的增加，荷载开始下降，墙体下部受压区域屈曲现象继续增加，墙体下部钢管束内混凝土逐渐被压溃，墙体下部受拉区域逐渐出现钢板被拉撕裂现象，最终下降到峰值荷载的85%，停止实验。最终试验现象为屈曲继续扩大，最终墙体下部出现成排屈曲，内部混凝土压溃；墙体下部受拉时墙体侧面与正面转角处出现裂口,试验裂口最终贯穿至整个侧面，导致构件失效，试验停止。试件YZQ5、YZQ6最终破坏形态如图4所示，其他墙体类似，限于篇幅，不予给出。3号墙体局部破坏形态如图5所示，可以清晰地看到其破坏形态。

试验结果对比如下：

(1) 墙体YZQ1～YZQ7当中，YZQ1、YZQ3、YZQ4、YZQ6、YZQ7破坏的主要原因为端部钢管束底部侧面钢板被撕裂，导致构件破坏，破坏现象中能看到，试件YZQ2,YZQ5破坏的主要原因为墙体整体出现扭曲，试件水平荷载下降较快，试件破坏，破坏现象中能看到墙体整体扭曲，及大量明显屈曲现象。YZQ6与其他墙体对比，边部钢管束为5 mm厚，中间钢管束为3 mm厚，5 mm厚钢管屈曲现象明显推迟，3 mm钢管在弹性阶段即出现混凝土与钢板脱离现象。

(a)试件YZQ5(b)试件YZQ6

图4 试件YZQ5、YZQ6破坏形态Fig.4 Failure modes of YZQ5 and YZQ6

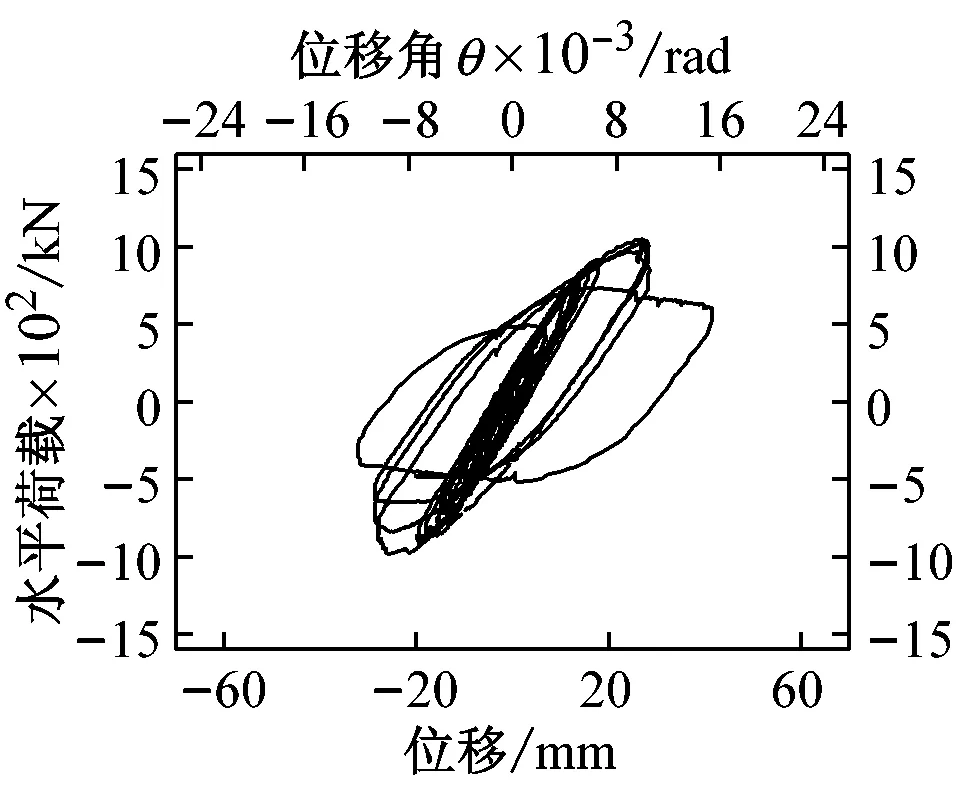
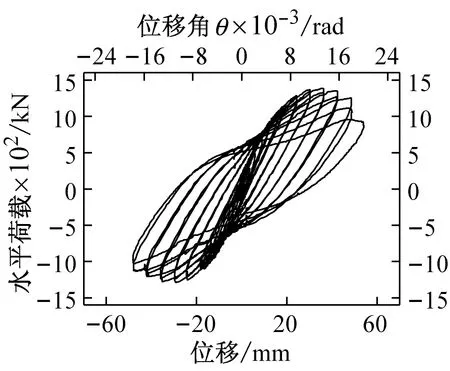
2.2滞回曲线

试件YZQ1～YZQ7的水平力-顶点位移滞回曲线如图6所示。由图可见：加载初期，各试件滞回曲线为一条直线，试件处于弹性阶段；在达到峰值荷载之前，滞回曲线为梭形，曲线饱满，无捏拢现象；试件到达峰值荷载之后，随着混凝土被压碎，钢板屈曲现象增多，最后端部钢管束底部侧面钢板被撕裂，构件失效，试件水平荷载下降缓慢，表现出试件具有良好的延性和变形能力。试件1与试件2对比，试件3与试件4、试件5对比可以判断出，轴压比为0.4时滞回曲线较0.6更为饱满，延性较好。试件2、试件4、试件6、试件7对比可以判断出，对于不同长度的墙体来说，位移角大致在1/83～1/100到达峰值，位移角在1/55～1/45最终失效，不同长度的墙体对构件的延性及位移并无明显影响。构件6的滞回曲线最为饱满，可以判断构件端部U型钢钢板加厚，构件的破坏阶段更为延后，U型钢截面尺寸较小时，墙体整体横向加劲肋更为密集，滞回曲线更为饱满。构件4、构件5对比可以看出，端部钢板布置栓钉，对端部钢板混凝土与钢板协同工作有一定影响，对结构整体影响较小。

(a) YZQ1

(b) YZQ2

(c) YZQ3

(d) YZQ4

(e) YZQ5

(f) YZQ6

(g) YZQ7图6 试件YZQ1～YZQ7顶点水平力-位移滞回曲线Fig.6 Hysteretic curves of YZQ1-YZQ7

2.3骨架曲线

骨架曲线是低周反复荷载作用下滞回曲线的外包络线，由各级加载第一循环的峰值点连接而成，各试件顶点荷载-位移骨架曲线如图7所示，各试件骨架曲线均为倒S形，表明试件的受力过程分弹性、塑性和破坏退化三个阶段。构件1轴压比为0.4，构件2轴压比为0.7，骨架曲线在峰值前非常接近，轴压比增大之后，到达峰值荷载之后，曲线下降较陡，位移显著变小。构件3～构件5中，构件3轴压比为0.4，构件4、构件5轴压比为0.6，同样可以判断轴压比较高时水平荷载到达峰值荷载后曲线下降变陡，变形能力降低。构件4与构件5对比骨架曲线基本重合，栓钉对构件整体影响较小，构件5因加工偏差原因，墙体出现面外整体弯曲，荷载下降较陡。通过构件2、构件4、构件6、构件7对比可以看到，随着墙体整体长度加长,水平荷载相应加大，其中构件6的U型钢截面最小，墙体内部加劲肋布置最为密集，荷载下降段曲线最为平缓。

图7 试件顶点水平力-位移骨架曲线Fig.7 Skeleton curves of test specimens

2.4剪切变形分析

钢板剪力墙结构的变形包括两部分，弯曲变形和剪切变形。因此结构的顶点位移也由两部分组成：由弯曲变形产生和由剪切变形产生。当剪力墙仅在平面内变形时，截面曲率沿高度不发生变化，那么弯曲变形不会使对角线方向发生变化，剪切变形产生的位移可以由式(1)计算，其中各符号的意义如图8所示[14]。

图8 剪切变形计算示意图Fig.8 Calculation diagram of shear deformation

(1)

各试件由剪切变形产生的顶点位移与总顶点位移对应情况如图9所示。图10为剪切变形占总变形比例。由图可见，各变形分量产生的顶点位移与总顶点位移基本呈线性关系，剪切变形产生的顶点位移占顶点总位移的50%左右。

图9 剪切变形-顶点位移曲线Fig.9 Curves of shear deformation-vertex displacement

图10 剪切变形占总变形比例Fig.10 Shear deformation to total deformation ratio

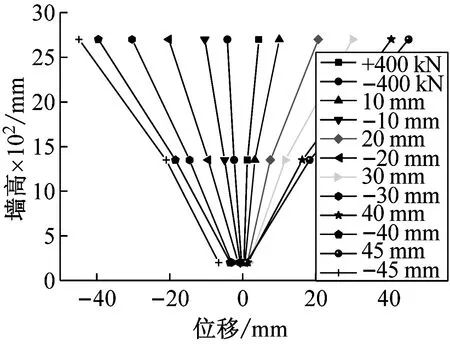
2.5墙体侧向变形

墙体不同高度的位移来考察墙体的竖向变形。在一字墙墙体上中下位置，200 mm高度，1 350 mm高度处，2 700 mm高度处布置位移计，测量墙体(由于试件制作与试验原因，墙体5出现平面外弯曲，其侧向变形不予给出)不同阶段侧向位移，如图11所示。根据试验中所测的数据，可绘制墙体在循环荷载下的相对变形。通过墙体侧向变形曲线可得出墙体加载前期，整体变形呈线性增长，随着位移增大，构件进入塑性变形，墙体上部位移增长较快。

2.6应变分析

在墙体及钢板布置应变花及应变片，测量钢板在试验过程中的应变状况。选取其中有代表性的构件YZQ3，YZQ4对其应变进行分析。钢板应变片布置如图12所示(V为竖向应变片)。

试验全过程，构件YZQ3、YZQ4侧壁一定位置竖向应变曲线如图13所示。

对于150 mm高度应变片来说：荷载加载的弹性阶段前期，即构件进入屈服之前，应变变化呈线性增长；当构件弹性阶段结束时，钢材应变接近或大于屈服应变，进入屈服阶段；随着荷载的增加到峰值荷载，钢板受压时，钢板的竖向压应变迅速增大，这与试验中观察到在试件峰值荷载时，钢板侧面出现较局部屈曲现象相吻合，而与之对应的同样荷载下，钢板受拉时，应力开始较快速增长，但相对于压应变较为缓慢；当水平荷载从峰值荷载开始进行下降时，构件开始因受压屈曲，钢板的竖向应变急剧增大，墙端部钢管边缘的压应变显著大于拉应变，与试验中钢板严重屈曲现象相吻合，这是由于墙底部钢板严重鼓曲及混凝土压溃所致。

(a) YZQ1

(b) YZQ2

(c) YZQ3

(d) YZQ4

(e) YZQ6

(f) YZQ7图11 不同水平位移墙体侧向位移图Fig.11 Lateral displacement of the wall at different horizontal displacement

图12 钢板应变片布置图Fig.12 Arrangement of strain gauge of the steel plate

对于450 mm高度应变片来说，在荷载加载的弹性阶段，应变变化呈线性增长，大多未进入屈服阶段，呈弹性增长，相对于150 mm高度应变片来说,相同荷载下应变明显较小。450 mm高度应变相对150 mm高度应变来说，相同荷载下应变明显较小，进入屈服阶段较晚，说明剪力墙底部首先屈服，随着荷载的继续加大，钢板的屈服逐渐向上延伸。

对于1 250 mm高度应变片来说,荷载-应变曲线始终处于线性变形，大部分钢板均未达到屈服阶段，可以得出：在滞回试验中，大部分钢板在1 250 mm以上区域均未达到屈服。

图14为YZQ3、YZQ4在墙体水平正向加载至不同位移角时墙体竖向应变。

通过墙体3、墙体4对比可得知：纵向应变在150 mm高度处，剪力墙受拉区域(2V、4V、5V)钢管束竖向应变初始时因受轴压比影响，承受压应变。随着位移角增加，水平荷载增大，剪力墙区域逐渐受拉，应变由初始受压应变变为受拉应变，随着位移角增大，应变逐步增大。墙体竖向应变随着距中心位置的增加，呈线性增长。墙体正向区域(6V、7V、8V)号应变，为剪力墙受压区域，初始时受轴压比影响，受到压应变，随着水平荷载的增加，应变逐渐增大，压应变随着距离墙中心的距离成比例上升。纵向应变在450 mm高度处，应变变化方式与在150 mm高度相似，墙体受拉区域，应变随着距离墙体中心距离增加，拉应变逐渐增加。墙体受压区域，随着距离墙体中心距离增加，压应变逐渐增加；构件到达峰值位移角之后，剪力墙两侧钢板束钢板开始进入屈曲，而中间钢板尚处于弹性阶段。

3 有限元分析

3.1有限元分析模型

为充分了解钢管束组合剪力墙的传力机制和应力分布规律，采用ABAQUS有限元软件建立了考虑几何非线性和材料非线性的三维有限元计算模型，对墙体在低周往复荷载作用下的受力性能进行了分析，考虑底部基础梁及上部加载梁对试验结果的影响，有限元模型及网格划分如图15所示。在有限元建模中，墙体的钢板与混凝土均由C3D8R模拟，使用扫略网格划分技术划分网格，钢管与混凝土表面之间的滑移采用有限滑移进行模拟，钢管与顶部盖板及底部基础梁之间采用绑定约束,钢管内部混凝土与顶部盖板及底部基础梁之间采用滑移接触。钢材本构包括弹性段和强化段，其中,强化段的弹性模量取值为0.01Es，Es为钢材的弹性模量。混凝土本构采用混凝土塑性损伤模型进行模拟[15]，混凝土应力应变曲线如图16所示。

(a) YZQ3下部150 mm处应变

(b) YZQ3下部450 mm处应变

(c) YZQ3下部1 250 mm处应变

(d) YZQ4下部150 mm处应变

(e) YZQ4下部450 mm处应变

(f) 1 250 mm处应变图13 YZQ3、YZQ4侧壁竖向应变图Fig.13 Vertical strain of the flank of YZQ3 and YZQ4

(a) YZQ3下部150 mm高度

(b) YZQ3下部450 mm高度

(c) YZQ4下部150 mm高度

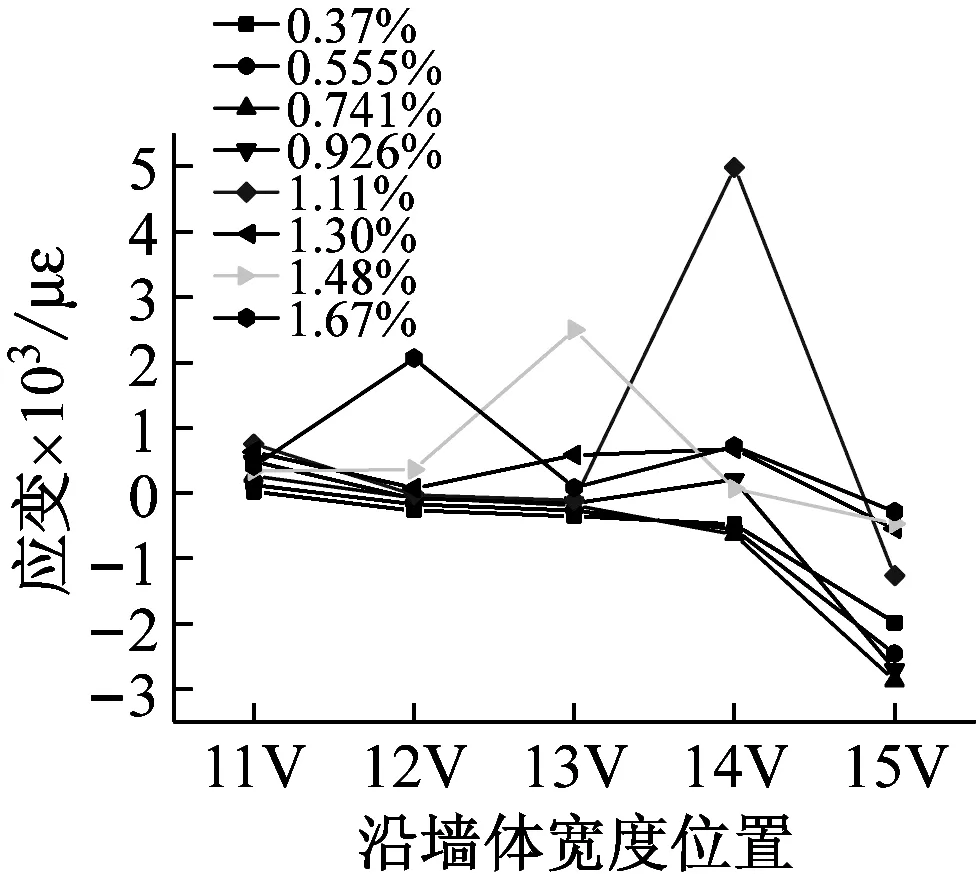
(d) YZQ4下部450 mm高度图14 YZQ3、YZQ4不同位移角墙体竖向应变Fig.14 Vertical strain of the YZQ3 and YZQ4 under different displacement angle

3.2有限元分析结果与试验结果对比

图17为除5号墙体之外(由于构件制作原因与加载偏差，5号墙体发生面外弯曲，不进行有限元拟合)的各试件的滞回曲线的试验结果与有限元分析结果的对比，图18为骨架曲线的对比。从图中可以看出:极限承载力误差在5%～10%左右,可见极限承载力有限元计算值与试验值吻合较好。由于试验过程中钢材初始缺陷、混凝土浇筑质量、后期钢材强化以及累积误差等原因，使得试件的极限承载力有限元计算值与试验值略有偏差。

(a)(b)

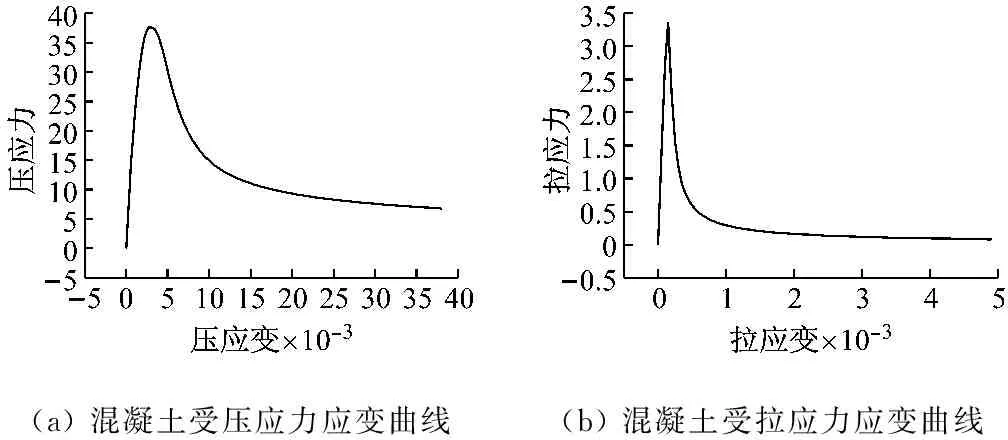
图15 有限元模型及网格划分Fig.15 Finite element model and meshing

3.3工作机理分析

为了研究钢管束组合剪力墙的各部分组件的应力、应变在不同阶段的分布状态和变化发展情况,选取了试验试件YZQ3为研究对象，对其在荷载-位移曲线上的几个特征点时的钢板应力状态进行分析。选取的具有代表性的特征点分别为:钢管束混凝土剪力墙达到屈服时、剪力墙试件达到极限荷载时以及最终破坏时所对应的受力状态，如图19所示。

(a) YZQ1 滞回曲线对比

(b) YZQ2 滞回曲线对比

(c) YZQ3 滞回曲线对比

(d) YZQ4滞回曲线对比

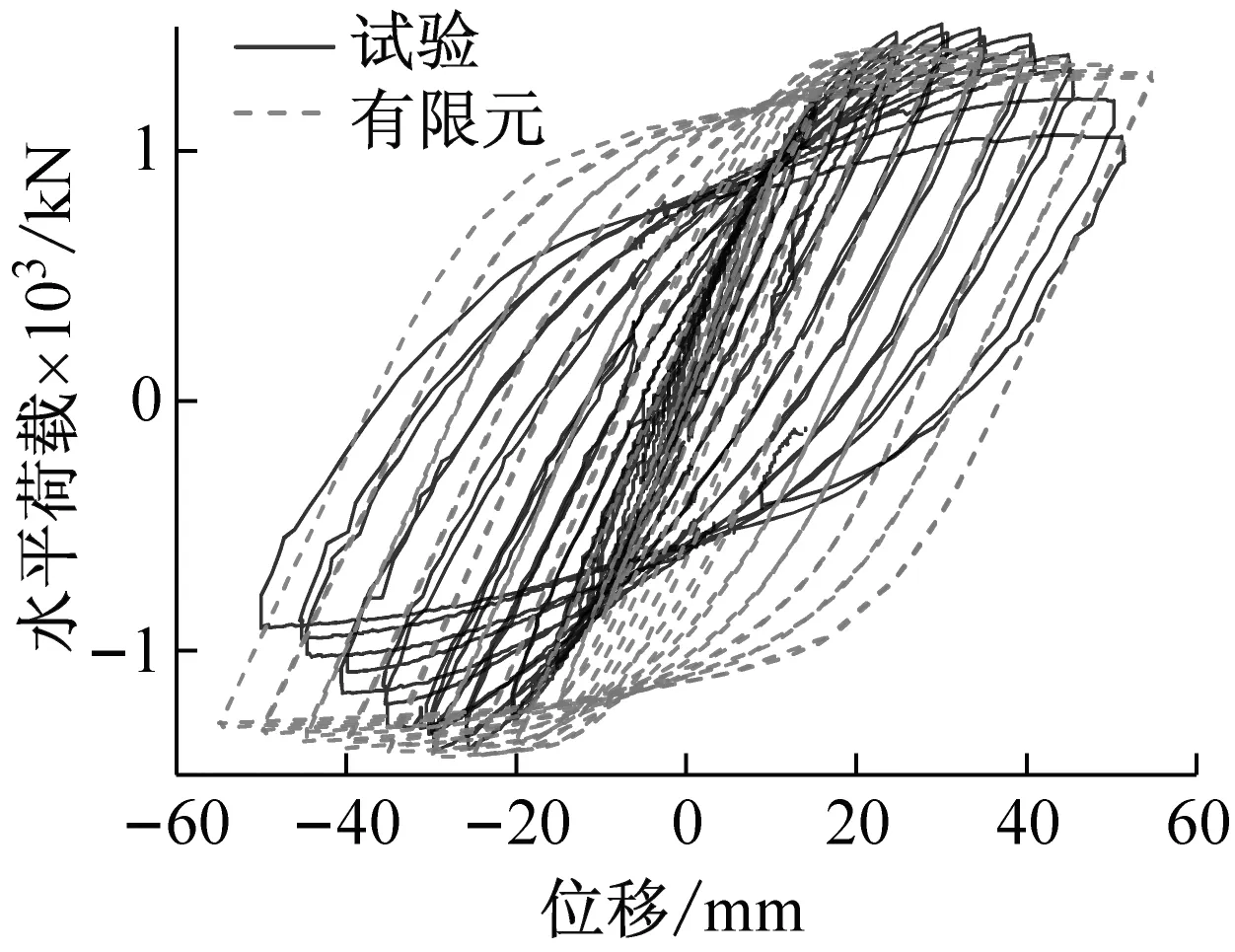
(e) YZQ6滞回曲线对比

(f) YZQ7滞回曲线对比图17 各试件的滞回曲线对比Fig.17 Comparison of hysteretic curves of specimens

(a) YZQ1骨架曲线对比

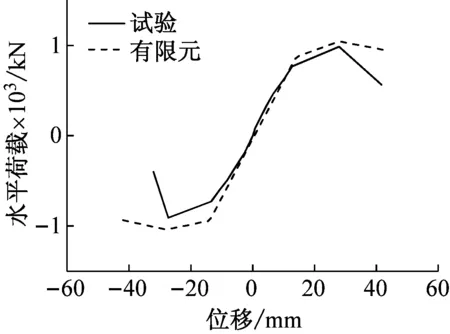
(b) YZQ2骨架曲线对比

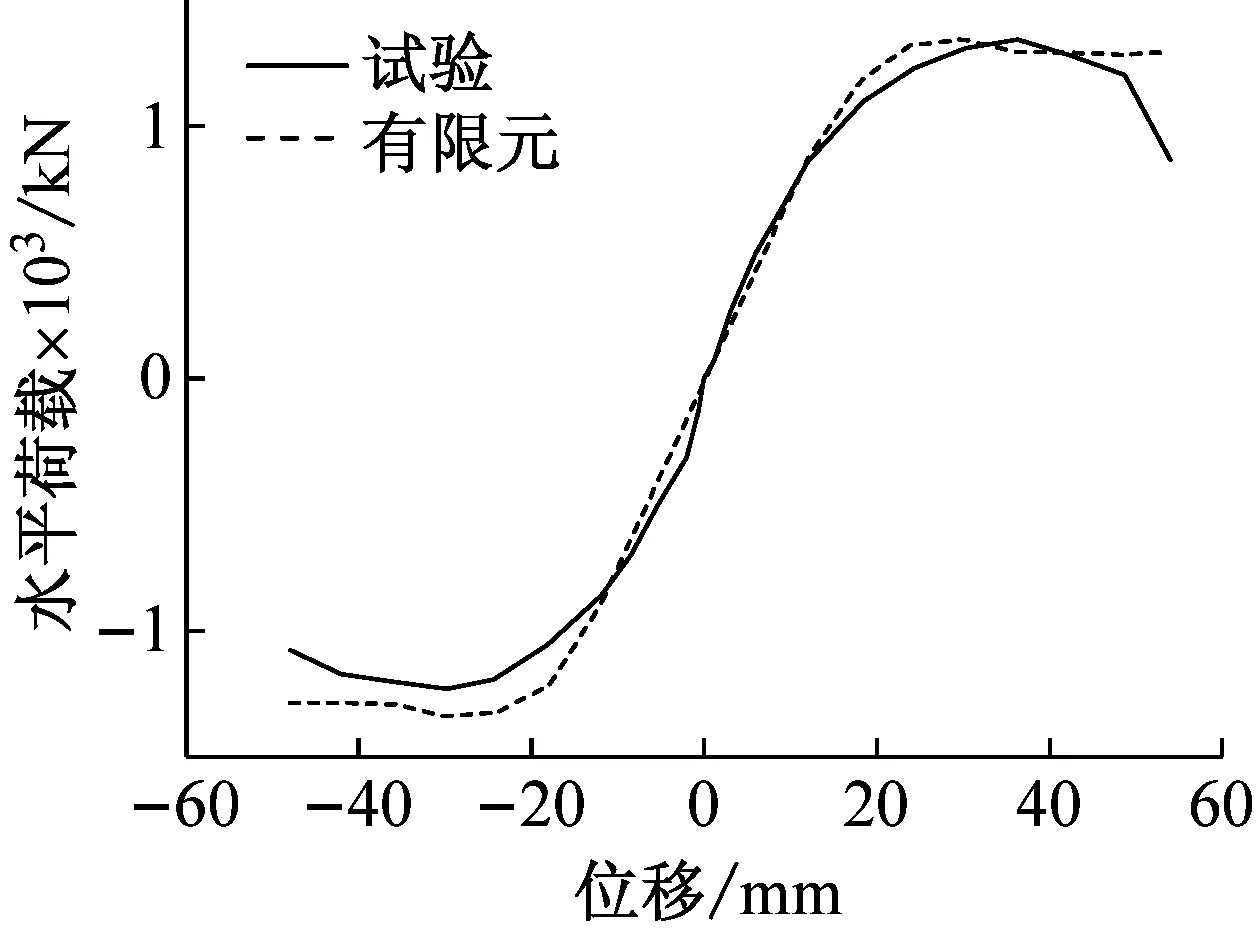
(c) YZQ3骨架曲线对比

(d) YZQ4骨架曲线对比

(e) YZQ6骨架曲线对比

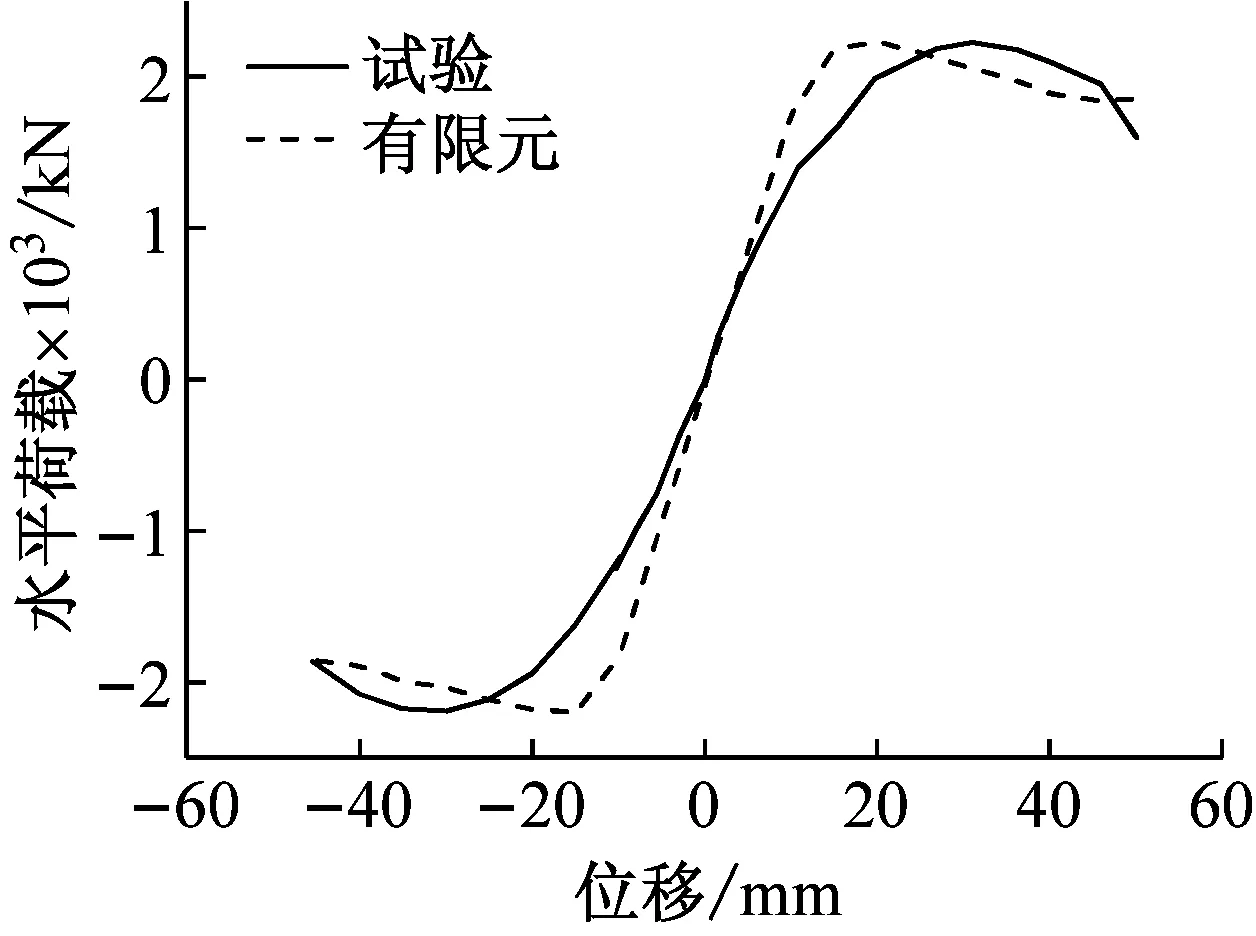
(f) YZQ7骨架曲线对比图18 各试件的骨架曲线对比Fig.18 Comparison of skeleton curves of specimens

(a) 墙体屈服阶段Mises应力云图

(b) 墙体极限荷载阶段Mises应力云图

(c) 墙体破坏荷载阶段Mises应力云图图19 墙体各阶段Mises应力云图Fig.19 Mises stress nephogram of the wallat different stage

可以看出，剪力墙下部钢板从开始屈服阶段到最终破坏阶段，钢板应力显著增大，在屈服阶段，钢管角部出现轻微屈曲。到达峰值荷载阶段，钢板底部的大部分区域已经超过钢板的屈服强度433 MPa，钢管束混凝土剪力墙底部从两侧起大部分钢板进入屈服阶段；与试验中出现的到达峰值荷载时，钢管束混凝土剪力墙，底部两侧钢板开始出现较明显的屈曲的现象可以对应。钢管束混凝土剪力墙到达最终破坏阶段，整个墙体底部钢板的应力进一步增大，下部500 mm以下绝大部分区域钢材强度超过屈服强度，图中可以看出底部钢板出现明显屈曲现象，钢管束混凝土剪力墙两侧钢管束侧边屈曲现象最为明显，表明钢材下部全面进入塑性变形，与试验现象中的，试验加载末期剪力墙底部出现成排屈曲，钢材进入屈服变形相对应；与应变分析中，下部钢板应变超过屈服应变相对应。

4 结 论

(1) 钢管束组合剪力墙具有良好的承载力、滞回曲线饱满，是一种抗震性能优越的剪力墙。

(2) 相同高度钢管束组合剪力墙极限荷载随钢板长度增大而增大，随轴压比增大而减小。

(3) 整个加载过程中，弯曲变形和剪切变形对顶点位移的贡献比例基本保持不变，剪切变形产生的顶点位移约占总顶点位移的50%。

(4) 端部钢管束布置栓钉会局部减小钢管屈曲，端部钢管束钢管壁加厚可延缓钢管屈曲并延缓钢管束端部侧面钢板撕裂现象。

(5) 构件端部U型钢钢板加厚，构件的破坏阶段更为延后，U型钢截面尺寸较小时，墙体整体横向加劲肋更为密集，滞回曲线更为饱满。

(6) 通过试验现象、应力应变分析及有限元分析可以看出，试件最终破坏均为下部钢板屈服，出现钢板受压屈曲或受拉撕裂及混凝土压溃导致破坏，钢板剪力墙上半部分完好，下部钢板大部分屈服。

(7) 墙体有限元模型结果与试验结果拟合较好，为钢管束组合剪力墙参数化分析以及公式推导提供良好基础。

[1] WRIGHT H. The axial load behaviour of composite walling[J]. Journal of Constructional Steel Research, 1998, 45(3): 353-375.

[2] WRIGHT H D, GALLOCHER S C. The behaviour of composite walling under construction and service loading[J]. Journal of Constructional Steel Research, 1995, 35(3): 257-273.

[3] 吕西林，干淳洁，王威. 内置钢板钢筋混凝土剪力墙抗震性能研究[J]. 建筑结构学报，2009，30(5)：89-96.

LÜ Xilin, GAN Chunjie, WANG Wei. Study on seismic behavior of steel plate reinforced concrete shear walls [J].Journal of Building Structures, 2009, 30(5): 89-96.

[4] ZHAO Qiuhong, ASTANEH-ASL A. Cyclic behavior of traditional and innovative composite shear walls[J]. Journal of Structural Engineering, 2004, 130(2): 271-284.

[5] LINK R A, ELWI A E. Composite concrete-steel plate walls: analysis and behavior[J]. Journal of Structural Engineering, 1995, 121(2): 260-271.

[6] EMORI K. Compressive and shear strength of concrete filled steel box wall[J]. Steel Structures, 2002, 68(2): 29-40.

[7] 聂建国，胡红松，李盛勇，等. 方钢管混凝土暗柱内嵌钢板-混凝土组合剪力墙抗震性能试验研究[J]. 建筑结构学报，2011，32(11)：74-81.

NIE Jianguo, HU Hongsong, LI Shengyong，et al. Experimental study on seismic behavior of steel plate reinforced concrete composite shear walls withsquare CFST concealed columns[J]. Journal of Building Structures, 2011, 32(11): 74-81.

[8] 聂建国，卜凡民，樊建生. 低剪跨比双钢板-混凝土组合剪力墙抗震性能试验研究[J]. 建筑结构学报，2011，32(11)：74-81.

NIE Jianguo, BU Fanmin, FAN Jiansheng. Experimental research on seismic behavior of low shear-span ratio composite shear wall with double steel plates and infill concrete[J]. Journal of Building Structures, 2011, 32(11): 74-81.

[9] 纪晓东，蒋飞明，钱稼茹，等. 钢管-双层钢板-混凝土组合剪力墙抗震性能试验研究[J]. 建筑结构学报，2013，34(6)：75-83.

JI Xiaodong, JIANG Feiming,QIAN Jiaru，et al.Experimental study on seismic behavior of steel tube-double steel plate-concrete composite shear walls[J]. Journal of Building Structures, 2013, 34(6): 75-83.

[10] 牟在根，张福建，李黎明. 两边连接竖向加劲式钢板剪力墙简化模型[J]. 天津大学学报(自然科学与工程技术版)，2014，35(11)：1631-1635.

MOU Zaigen, ZHANG Fujian,LI Liming.Simplified model for two-side constraint steel plate shear wall(SPSW)with vertical stiffeners [J]. Journal of Tianjin University(Science and Technology),2014,35(11):1631-1635.

[11] ZHANG Xiaomeng, QIN Ying, CHEN Zhihua.Experimental seismic behavior of innovative composite shear walls [J].Journal of Constructional Steel Research, 2016, 116: 218-232.

[12] 李忠献. 工程结构试验理论与技术[M].天津：天津大学出版社，2004.

[13] 杨亚彬，曹万林. CFST边框内藏桁架高剪力墙抗震试验与有限元分析[J]. 振动与冲击，2014，33(11)：107-113.

YANG Yabin, CAO Wanlin.Seismic testing and finite element analysis of shear wall with CFST columns and concealed trusses[J]. Journal of Vibration and Shock,2014,33(11):107-113.

[14] BEYER K, DAZIO A, PRIESTLEY M J N. Shear deformations of slender reinforced concrete walls under seismic loading[J]. ACI Structure Journal, 2012, 109(1): 127-12.

[15] 韩林海，陶忠，王文达. 现代组合结构和混合结构—试验、理论和方法[M].北京：科学出版社，2009.

Deformationpropertyandfiniteelementanalysisofanewtypeofsteeltubebundlecompositeshearwalls

CHEN Zhihua1,2，JIANG Yuting2，ZHANG Xiaomeng2，YANG Qiangyue3，LI Wenbin3，HU Lili3，LI Jie2

(1. State Key Laboratory of Hydraulic Engineering Simulation and Safety，Tianjin University，Tianjin 300072，China；2. School of Civil Engineering，Tianjin University，Tianjin 300072，China；3. Hangxiao Steel Structure Co., Ltd., Hangzhou 310003, China)

A new type of steel plate shear walls-steel tube bundle composite shear walls was proposed. Seven steel tube bundle composite shear walls were tested under cycle load, and their hysteretic curves and skeleton curves were analyzed. The deformation property and strain performance of walls as well as their failure modes under different stages were discussed. Based on the experiments, the mechanical property of the composite shear walls was simulated by using the software ABAQUS. The results show that the steel tube bundle composite shear walls have high bearing capacity and good seismic performance. In order to compare their bearing mode, the effects of different parameters including the section of steel tube bundle, the thickness of steel plate, the shear span ratio and the condition whether the stud was decorated were analyzed. The experimental phenomenon, stress-strain analysis and finite element simulation show that the eventual damage of the specimens usually comes from the compression buckling or tension tear of the steel plate and the concrete crushing at the lower part of the walls.

steel tube bundle composite shear wall; experimental study; deformation analysis; failure mode; finite element analysis

TU398

A

10.13465/j.cnki.jvs.2017.19.006

国家自然科学基金(61272264)

2016-01-05 修改稿收到日期：2017-07-21

陈志华 男，博士，教授，博士生导师，1966年生

张晓萌 男，博士生，1983年生