整车气动声学风洞的冷却与加热系统

高艳芳，李田田，陈 力，庞加斌

（同济大学 汽车学院 同济大学上海市地面交通工具风洞中心，上海 201804）

整车气动声学风洞的冷却与加热系统

高艳芳，李田田，陈 力，庞加斌

（同济大学 汽车学院 同济大学上海市地面交通工具风洞中心，上海 201804）

整车气动声学风洞是汽车空气动力学和声学设计及性能开发的关键试验设施，对增强自主研发能力必不可少。风洞冷却与加热系统是保证试验准确性的必要设施。为了优化设计风洞冷却与加热系统，以同济大学气动声学风洞为实例，根据风洞结构特点对热边界层进行分类，更为准确地计算了冷却与加热系统的冷热负荷，建立了气动声学风洞的热力学模型。初步分析显示，风洞冷却与加热系统可通过优化设计，降低系统的安装功率，达到节能降耗的目的。

气动声学风洞；冷却与加热系统；负荷计算；热力学模型；优化设计

随着汽车工业的发展，消费者对汽车性能的要求越来越高，空气动力学和风噪声性能的研发也越来越受到国内企业的重视，风洞已经成为国内汽车行业必不可少的试验设施。

整车气动声学风洞主要用于模拟车辆在实际道路上的运动学条件，准确测量汽车受到的气动力和风噪声水平。通过对比分析，在造型设计、工程成本、燃油经济性、动力性和舒适性的综合要求之间寻找最佳设计方案，涉及汽车设计、零部件开发、汽车制造和运行全过程。

引用格式：

1929年起风洞开始用于汽车试验[1]，1970～1980年之间气动声学风洞开始出现[2]，至今相关试验技术已发展成熟。现有气动声学风洞喷口尺寸约为25 m2，最高风速在200～300 km/h之间，当风洞风速为160 km/h时，背景噪声水平约60 ～ 70 dBA[3]。

现代汽车的开发周期不断缩短，成本控制严格，技术要求持续提高，对汽车风洞试验质量的要求也逐渐提高，需要保证风洞模拟环境的稳定性及试验设备的可靠性。对于封闭的回流式风洞，连续运行使风洞流道温度逐渐升高，同时夏季高温和冬季低温也会使流道温度不稳定。

气流温度不稳定对风洞试验的影响有：（1）仪器设备的工作温度波动，使测试精度或工作状态不稳定。（2）温度变化影响试验数据准确性。（3）试验对象的材料因温度变化而变化，如油泥模型、密封件隔声性能。因此，整车气动声学风洞需要冷却与加热系统，保证内部气流温度稳定在一定范围内，不受试验连续运行和季节变化的影响。

整车风洞尺寸大，能耗大，相对应的冷却与加热系统功率也大，设备投资成本与系统运行维护成本高。气动声学风洞在结构和材料上与一般建筑不同，冷却与加热系统冷热负荷计算方式也应不同。此外，风洞实际试验过程具有明显的间断性运行特点，这与传统的设计准则要求（考虑风机连续运行）偏离很大。若按照风洞实际试验过程设计冷却与加热系统，理论上可降低系统设备投资，减小运行维护成本。

本研究以同济大学气动声学风洞为典型实例，根据风洞结构进行热边界分类，建立风洞传热热力学模型，计算风洞冷热负荷。然后，将风洞冷却与加热实际所需功率与系统设计功率相对比，验证了通过对热边界分类计算风洞冷热负荷，对冷却与加热系统进行优化，降低风洞成本的可行性。

1 同济大学气动声学风洞冷却与加热系统

1.1 同济大学气动声学风洞结构

同济气动声学风洞为回流式结构，可减小所需风机功率，并有助于控制流道气流温度，降低风洞背景噪声[4]。风洞结构主要可分为收缩段（喷口）、试验段、扩散段、转角段、连接段、稳流段等。同济大学气动声学风洞结构如图1所示。

图1 同济大学气动声学风洞结构图

同济大学气动声学风洞喷口尺寸为27 m2，最高风速为250 km/h，在风速160 km/h时，风洞背景噪声仅为61 dBA，是世界最安静的风洞之一。风洞配备五带路面模拟系统与边界层控制系统，可准确模拟真实汽车行驶状态的流场。风洞流道内装有热交换器，与空调机组协作可将气流温度控制在20～30 ℃。作为中国第一座汽车整车风洞，同济风洞对中国汽车工业的自主研发做出了重要贡献。

1.2 风洞冷却与加热系统特点

在气动声学风洞试验中，需要试验环境温度保持在一定范围内，从而保证试验准确性。同济大学气动声学风洞冷却与加热系统可分为用于制冷的流道换热器系统和用于加热的空调机组系统。

风洞冷却和加热系统与典型建筑或房间空调系统相比，不同之处主要在于[5]：

（1）气动声学风洞的多段式结构与房间整体式结构差别较大，负荷计算有所不同。

（2）风洞冷却和加热系统运行与试验过程同步，间歇性工作。

（3）风洞冷却和加热系统响应快，要求环境温度在短时间内达到并处于稳定状态。

（4）风洞内大功率风机对冷、热负荷量有较大影响。

（5）同济大学风洞为回流式风洞，温度不受外界影响，湿度对风洞气动和声学测试影响不大，可忽略。

1.3 同济大学风洞冷却系统

同济大学风洞冷却是通过流道中的翅片管式热交换器实现的[6]。流道换热器冷却效率高，且能产生较为均匀的温度场，被很多风洞采用。换热器由制冷机组提供冷却液，风洞内高温气体通过换热器时，与低温液体发生热量交换，气体温度降低，空气在流道内循环时，温度得到控制，如图2所示。

1.4 同济大学风洞加热系统

同济大学风洞加热与新风系统，如图3所示。通过控制阀门的开关，可实现新风模式与回风模式 的转化。新风模式下空调机组对风洞进行通风换气，保证流道气体的洁净；回风模式下气体在回路中循环，空调机组对气流进行加热，使流道温度达到试验要求。

图2 同济气动声学风洞冷却系统-流道热交换器系统

图3 同济大学气动声学风洞加热系统-空调机组

2 同济大学生气动声学风洞传热模型

2.1 负荷计算

风洞冷却与加热系统工作分为升（降）温过程和温度维持过程。因此，冷却与加热系统负荷主要包括风洞升（降）温负荷、风洞墙体传热和风洞内部热源散热3部分。

2.1.1 风洞墙体传热

同济大学气动声学风洞为回流式结构，在试验段、第一扩散段、风扇等位置处覆盖有消声板、喷口和风机为钢结构，外墙材料主要为混凝土。进行热负荷计算时，根据热边界类型分类，见表1。将风洞墙体与外界传热过程假设为通过平壁的稳态导热，不同边界类型传热如图4所示。

多层平壁传热过程热流量计算如下：

式中：h1为强迫对流系数，W/(m2·K)；h2为自然对流系数，W/(m2·K)；λ为材料热导率，W/(m·K)；为材料厚度，m；A为传热边界面积，m2；tf1为风洞流道温度，K；tf2为风洞外界环境温度，K；n为传热边界层数。

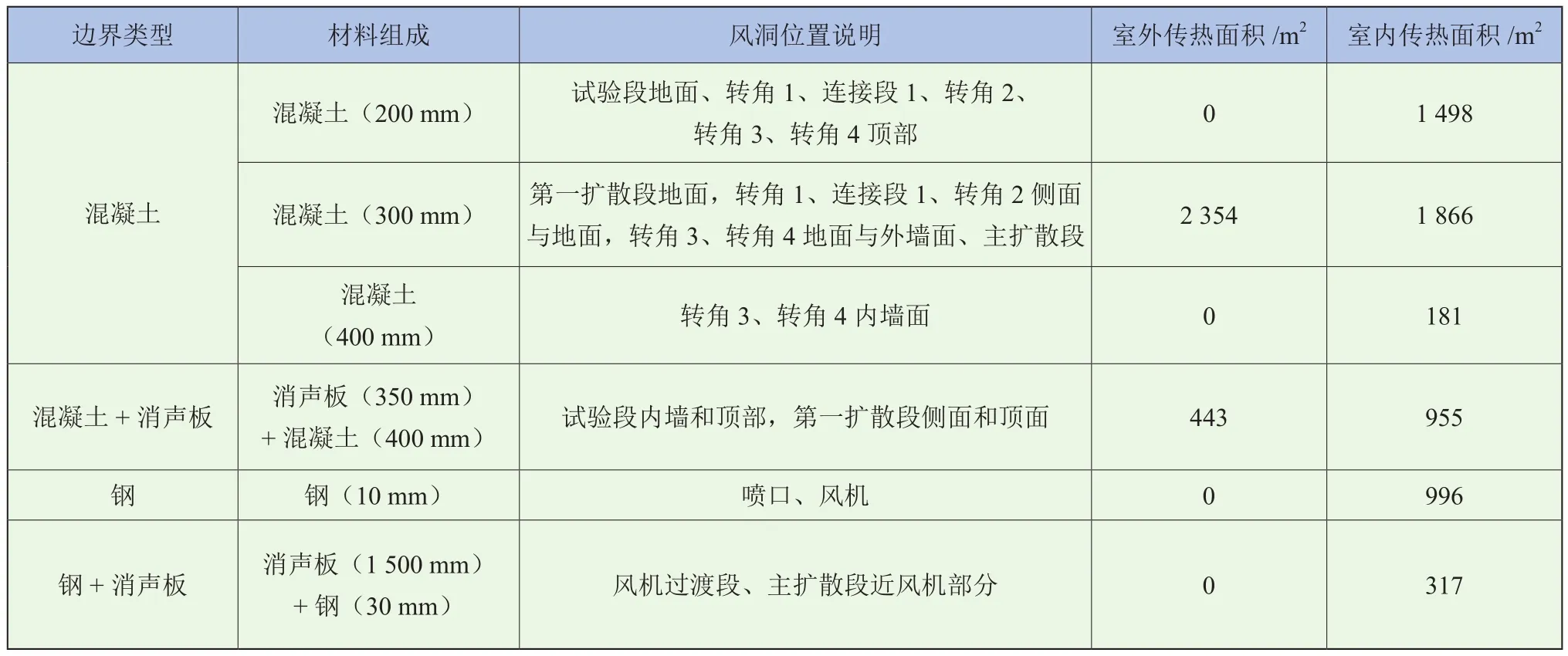
表1 风洞热边界分类表

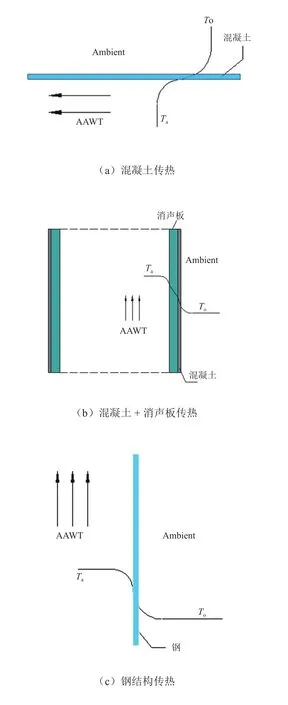
图4 不同边界类型传热示意图

对风洞4种边界类型传热热流量进行计算并叠加，即可得到整个风洞的传热热流量。

式中：Φ为热流量，W。

2.1.2 风洞内部热源散热

风洞内部热源主要是风机。风机做功绝大部分用于克服气流在流道内的压力损失，最终转化为气流内能，使风洞温度升高。

同济风洞风机设计功率为4×106W，最大风速250 km/h，不同风速V下风机做功转化成气体的热量为：

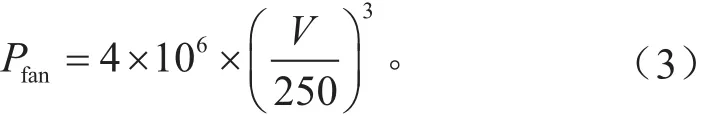
式中：Pfan为风机散热功率，W。

2.1.3 风洞升（降）温负荷

夏季风洞内部温度过高需要降温，冬季风洞内部温度过低需要升温。风洞内部气体加热（降温）到指定温度所需的能量即为风洞升（降）温负荷。这一过程所需热量计算公式为：

式中：Cp为空气的定压比热容，J/(kg·K)；m为流道内部所有空气质量，kg；Δt为温度变化值。

限定升（降）温所需的时间T，则有风洞升（降）温所需功率：

2.2 传热数学模型

风洞与外界传热受外界环境温度变化影响。春秋季时，风洞内外温差不大，忽略外部传热，且不考虑升（降）温过程，冷却负荷仅考虑风机做功Pfan；夏季时，风洞外界温度高，降温过程冷却负荷要考虑风洞降温做功Pcooling、风机做功Pfan和外界传热Φin，温度维持过程需考虑风机做功Pfan和外界传热Φin；冬季时，风洞外界温度低，但风机是内部热源，升温过程加热负荷要考虑风洞升温做功Pheating，风洞对外传热Φout，温度维持过程需考虑风机做功Pfan和风洞对外传热Φout。

春秋季冷却系统所需功率：

夏季降温过程冷却系统所需功率：

夏季温度维持过程冷却系统所需功率：

冬季升温过程加热系统所需功率：

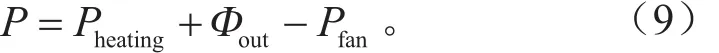
冬季温度维持过程加热系统所需功率：

2.3 参数取值及初步计算结果

2.3.1 风洞墙体传热计算

由式（1）可知，计算风洞传热热流量需要知道各边界的导热率，以及强迫对流和自然对流的换热系数。

混凝土结构热导率为1.2 W/(m·K)，消声材料热导率为0.052 W/(m·K)，钢结构热导率为50.2 W/(m·K)[7]。

假设风洞流道内部与壁面传热过程为常壁温外掠平板紊流平均传热[8]，则有：

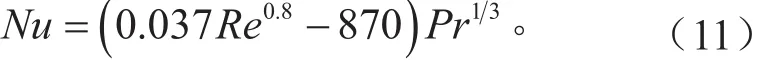
式中：Re为雷诺数；Pr为普朗特数，其适用范围为0.6≤Pr≤60，5×105≤Pr≤108。

假设风洞外壁与外界传热过程为自然对流传热，根据章熙民和朱彤提出的公式有[8]：

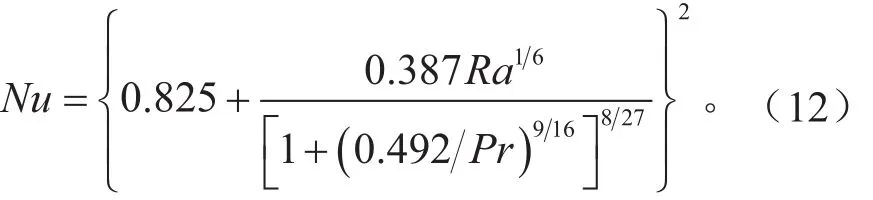
式中：Nu为努塞尔数；瑞利准则Ra = Gr⋅ Pr，格拉晓夫准则为运动粘度；体积膨胀系数α=，单位1/K。

努赛尔数与对流换热系数关系为：

式中：h为对流换热系数，W/(m2·K)；l为平板特征长度，m；λ为热导率，W/(m·K)。

同济大学气动声学风洞常用试验风速为120～160 km/h，计算时选取风速160 km/h。假设上海夏季外界温度为40 ℃，冬季外界温度为-10 ℃，风洞流道温度需要保持在25 ℃。不同定性温度下的空气属性可查看参考文献[8]附录2，再根据式（11）～（13），按照风洞结构类型计算自然对流和强迫对流换热系数，见表2。

表2 自然对流和强迫对流换热系数计算 单位：W/(m2·K)

由表2可知，风洞不同结构处的强迫对流换热系数差异较大，这是由于不同结构处气流速度是不同的。而不同结构处自然对流换热系数差异较小，取平均值可获得室外风洞外壁自然对流换热系数h2夏季时为3.20 W/(m2·K)，冬季时为4.44 W/(m2·K)。根据风洞建筑结构特点，假设室内的风洞外壁自然对流换热系数值为室外的一半。

表3为按式（1）和式（2）计算得到的风洞不同类型边界传热热流量和总传热热流量。在风洞内部保持25 ℃，夏季外界环境温度为40 ℃，冬季外界环境为-10 ℃，试验风速为160 km/h时，夏季外界对风洞传热量为：

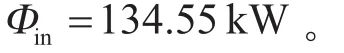
冬季风洞对外传热量：

表3 风洞传热热流量 单位：W

2.3.2 风机散热计算

由式（3）可知，在最大试验风速为250 km/h时，风机持续运行散热功率为4 000 kW。而在试验过程中风机间歇性运行，实际散热功率较小。根据同济大学风洞的试验纪录，可将气动声学风洞试验分为高铁试验、雷诺数试验、造型优化试验三种典型试验工况，计算三种试验工况下风机的最大散热量，继而确定冷却与加热系统功率。若风洞试验存在极限工况（高风速长时间运行），冷却系统功率不足时，冷却系统中的蓄冷罐发挥作用，控制气流温度。在试验过程中，冷冻机组持续运行, 多余制冷量存储在蓄冷罐中，以保证风机间歇运行冷却能量的需求，控制气流温度。风机散热量计算过程如下。

2.3.2.1 高铁工况

高铁工况所需风速为250 km/h，试验时间3 min，工况准备时间10 min，如图5所示。由计算可知，风机散热平均功率为

图5 高铁工况示意图

2.3.2.2 雷诺数及偏角扫略工况

雷诺数及偏角扫略工况风机处于持续运行状态，雷诺数扫略时风机在每个风速下稳定3 min，偏角扫略时风速稳定不变，天平改变偏角，如图6所示。由计算可知，风机散热平均功率为Pfan.avg=722. 1kW 。

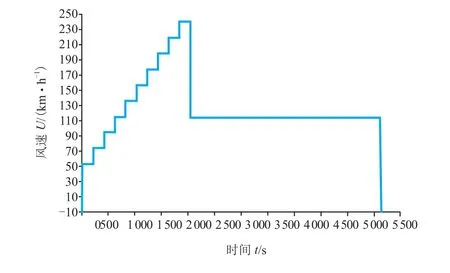
图6 雷诺数及偏角扫略工况

2.3.2.3 造型优化工况

造型优化工况风速140 km/h，试验时间3 min，工况准备时间10 min，如图7所示。由计算可知，风机散热平均功率为Pfan.avg= 156. 0 k W 。

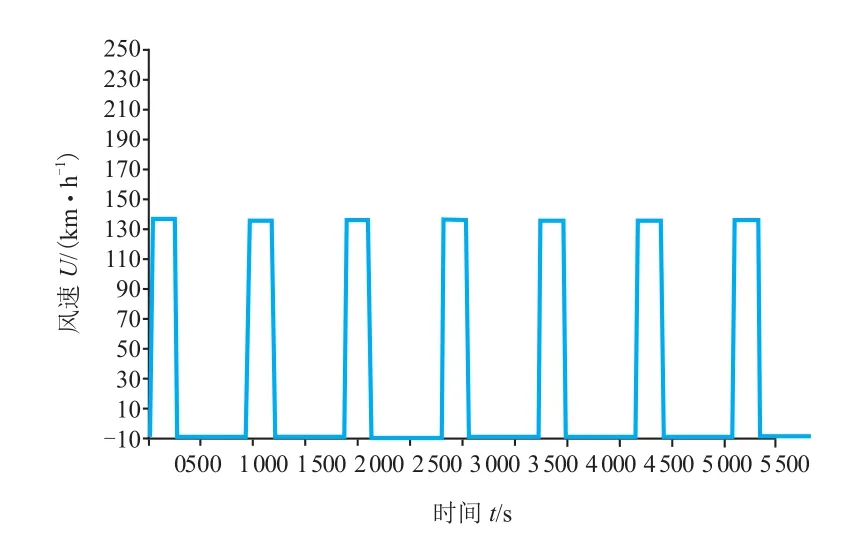
图7 造型优化工况

由分析可知，实际试验过程中平均风机散热功率仅为风机最大功率的21.6%，选取Pfan= 864. 6kW为风机散热功率。

2.3.3 风洞升（降）温计算

风洞内部流道体积V=23 590 m3，假设夏季风洞内部温度需要从40 ℃降至25 ℃，冬季风洞温度需要从-10 ℃升至25 ℃，限定升降温时间T=0.25 h，根据式（4）和式（5）可以得到夏季风洞降温所需冷却功率：

冬季风洞升温所需加热功率：

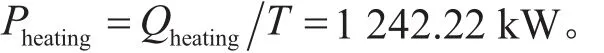
2.3.4 风洞冷却和加热系统负荷计算

风洞冷却和加热系统负荷按照式（6）～（10）计算。

春秋季冷却系统所需功率：

夏季降温过程冷却系统所需功率：

夏季温度维持冷却系统所需功率：

冬季升温过程加热系统所需功率：

冬季温度维持加热系统所需功率：

通过比较可知，风洞冷却和加热系统所需最大冷却功率不足1 500 kW ，所需最大加热功率约为1 400 kW ，且冬季试验过程中还需冷却系统工作。

3 结论

本文对风洞冷却和加热系统做了简单介绍。在风洞与外界传热问题上，对风洞各段表面进行热边界层分类，分别计算不同边界层状态下的传热速率。针对风机散热功率计算，提出了较为准确的计算风洞冷热负荷的方法。

经过初步计算，风洞实际所需冷却系统功率不足1 500 kW，加热系统功率约为1 400 kW，而风洞原设计冷却系统功率为4 200 kW，可对冷却和加热系统进行优化设计，降低设备投资及维护成本。

本文中的风洞冷热负荷计算方法对未来风洞冷却和加热系统设计也有一定的参考价值。

参考文献（References）：

[1]ESPER A H. Early Wind Tunnel Testing at Ford [C]//SAE National Automobile Week，Detroit，1960：3-5.

[2]VANGORDON C L，WALTER J. Overview of Wind Tunnel Testing for Automotive Development [C]//SAE Technical Papers，2008-28-0007，2008：4-8.

[3]TADAKUMA K，SUGIYAMA T，MAEDA K，et al.Development of Full-Scale Wind Tunnel for Enhancement of Vehicle Aerodynamic and Aero-Acoustic Performance[C]//SAE Technical Papers，2014-01-0598，2014：6-13.

[4]艾伦·波普，约翰J·哈珀. 低速风洞试验[M]. 彭锡铭，严俊仁，石佑伦，等，译. 北京：国防工业出版社，1977：35-49.POPE A，HARPER J. Low-speed Wind Tunnel Testing[M]. PENG Ximing，YAN Junren，SHI Youlun，et al，Translate.Beijing：National Defence Industry Press，1978：35-49. (in Chinese)

[5]赵兰萍，王振亚，庞加斌. 汽车整车环境模拟(气候)风洞 [C]//上海制冷学会学术年会论文集，上海，2005：2-3.ZHAO Lanping，WANG Zhenya，PANG Jiabin.Automotive Climatic Wind Tunnel [C]//Shanghai Refrigeration Learn Academic Essays，Shanghai，2005：2-3.(in Chinese)

[6]李启良. 气动一声学风洞热交换器的数值模拟与试验研究 [D]. 上海：同济大学，2007：15-16.LI Qiliang. Numerical Simulation and Experimental Study on Heat Exchanger of Aero-Acoustic Wind Tunnel [D].Shanghai：Tongji University，2007：15-16.(in Chinese)

[7]弗兰克·P·英克鲁佩勒，大卫·P·德维特，狄奥多尔·L·伯格曼，等. 传热与传质基本原理 [M]. 葛新石，叶宏，译. 北京：化学工业出版社，2007：572-573.INCROPERA F P，DEWITT D P，BERGMAN T L，et al. Fundamentals of Heat and Mass Transfer [M]. GE Xinshi，YE Hong，Translate. Beijing：Chemical Industry Press，2007：572-573.(in Chinese)

[8]章熙民，朱彤. 传热学[M]. 北京：中国建筑工业出版社，2014：163-167.ZHANG Ximin，ZHU Tong. Heat Transfer Theory [M].Beijing：China Architecture & Building Press，2014：163-167.(in Chinese)

Full-scale Aero-acoustic Wind Tunnel Cooling and Heating Systems

GAO Yanfang，LI Tiantian，CHEN Li，PANG Jiabin
（Shanghai Automotive Wind Tunnel Center，The School of Automobile Studies，Tongji University，Shanghai 201804，China）

The full-scale automotive aero-acoustic wind tunnel is one of the vital test facilities for vehicle aerodynamics and acoustics design and performance development. It's indispensable for increasing the capability of self-brand research and development. The wind tunnel cooling and heating system is necessary to ensure the accuracy of the testing. In order to optimize the design of wind cooling and heating system, this paper classified the thermal boundary layers, calculated the cooling-heating load, and developed the thermodynamic model on the basis of the aero-acoustic wind tunnel at Tongji University. The preliminary study shows the optimized design can reduce energy consumption of the wind tunnel cooling and heating system.

aero-acoustic wind tunnel；cooling and heating system；load calculation；thermodynamic model；optimal design

V211.74

A

10.3969/j.issn.2095-1469.2017.05.09

2017-03-29 改稿日期：2017-04-28

高艳芳，李田田，陈力，等. 整车气动声学风洞的冷却与加热系统 [J].汽车工程学报，2017，7(5)：374-381.

GAO Yanfang，LI Tiantian，CHEN Li，et al. Full-scale Aero-acoustic Wind Tunnel Cooling and Heating Systems [J]. Chinese Journal of Automotive Engineering，2017，7(5)：374-381. (in Chinese)

作者介绍

责任作者：高艳芳（1991-），女，河南周口人。硕士研究生，主要研究方向为车身与空气动力学。

Tel：18817366541

E-mail：gaoyanfangabc@163.com

庞加斌（1970-），男，湖北随州人。博士，教授级高级工程师，主要研究方向为车身与空气动力学。

Tel：021-69589109

E-mail：pang@tongji.edu.cn