带Poisson跳随机资本系统数值解的稳定性

郑来运

(宁夏大学 机械工程学院， 银川 750021)

带Poisson跳随机资本系统数值解的稳定性

郑来运

(宁夏大学 机械工程学院， 银川 750021)

随机资本系统；数值解；Poisson 跳；稳定性

考虑如下带Poisson跳的役龄相关随机资本系统：

(1)

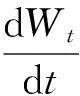
对于役龄相关的确定性资本系统(不含随机扰动项)，研究者们曾进行了大量的研究。例如Feichtinge等[1]建立了确定性役龄相关投资系统并给出了最优控制的必要条件，发展了一种带有技术进步的役龄相关资本积累模型[2]；Goetz[3]研究了工厂资本替换决策中的投资回报决策和最优控制问题。带Poisson跳役龄相关随机资本系统(1)是确定性资本系统[4]的扩展，它将随机环境噪声的影响考虑到模型中，能较好地描述动力系统中结构的突然变化等[5]，从而使模型更符合实际，近年来受到了广泛关注。事实上，一般很难或无法获得该系统的解析解，因此，研究者们更加关注随机微分方程数值解的研究[4,6-17]。例如，Li等[6]讨论了具有Markovian调制的随机时滞微分方程数值解的收敛性和稳定性；Pang等[7]研究了年龄相关随机种群系统数值解的指数稳定性；Wang等[8]研究了带 Poisson 跳和 Markovian调制的随机时滞微分方程数值解的收敛性，并讨论了带Poisson跳年龄相关随机种群系统半隐式Euler数值解的收敛性[9]；Rathinasamy[10]讨论了具有Markovian调制的年龄相关随机种群系统分裂步数值方法的收敛性；Ding等[11]研究了随机微分方程分裂步方法的收敛性和稳定性；Cui等[12]分析了带时滞和Poisson跳的随机中立偏微分方程的指数稳定性。最近，徐丽丽[13]对几类带Poisson跳的非线性随机延迟微分方程数值算法的稳定性进行了分析；张启敏等[14-16]研究了具有扩散的年龄相关随机种群系统数值解的指数稳定性、一类带随机跳系数的役龄相关随机资本系统数值解的收敛性，以及具有Markovian调制的随机年龄结构种群系统半驯服Euler法的指数稳定性。本文主要讨论给定条件下带Poisson跳的役龄相关随机资本系统Euler数值逼近解的指数稳定性。

1 预备知识和Euler逼近

这里V′=H-1([0,A])是V的对偶空间；|·|和‖·‖分别表示V和V′中的范数；〈·,·〉表示V与V′之间的对偶积；(·,·)表示H中的数量积；K是一个实可分Hilbert空间。算子B∈L(K,H)是所有K到H的有界线性算子空间，‖B‖2为Hilbert-Schmidt 范数，即

定义1 若(Ω,F,{Ft},P)为随机基，Wt是一个 Wiener过程。设随机变量K0满足E|K0|2<∞，若Kt满足条件：

1)Kt是一个Ft-可测随机变量；

3)Kt满足方程：

(2)

(3)

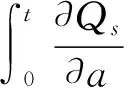
(4)

其中Zt为阶梯函数，定义为

假定役龄相关随机资本系统(1)满足如下条件：

① (Lipschitz条件)存在常数M>0，对任意x,y∈H,有|f(t,y)-f(t,x)|∨g(t,y)-g(t,x)2∨|h(t,y)-h(t,x)|≤M|y-x|;

④f(t,0)=0,h(t,0)=0,g(t,0)=0,t∈[0,T]。由文献[17]可证明：若上述条件成立，则系统(1)在(a,t)∈Q上存在唯一解K(a,t)。

2 相关引理

本小节给出用于证明主要结论的相关引理。

引理1 若条件① ～ ④成立，则存在常数C1>0(C1与Q0和T有关)，使得

(5)

该引理的证明与文献[18]的方法类似，这里不做赘述。

引理3 若条件①～ ④成立，则存在常数C2，使

(6)

证明：对任意的t∈[0,T]，存在正整数m，使得t∈[mh,(m+1)h)，有

于是，

应用Cauchy-Schwarz不等式和条件①、②和④，有

应用条件①和④及Burkholder-Davis-Cundy不等式，得

和

由此可得式(6)，且

证毕。

3 数值解的稳定性

由引理1～3，可证明在给定条件①～ ④下，带Poisson跳的役龄相关随机资本系统的数值解具有如下定理成立。

定理1 若条件①～ ④成立，则对任意的T，存在常数C5(依赖于T但与h无关)，使

(7)

证明：对由式(1)和式(4)，有

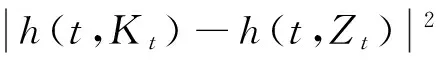
(1+λ)M2|Kt-Zt|2dt+2(Kt-Qt,(g(t,Kt)-g(t,Zt))dWt)+

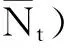
于是，对∀t∈[0,T]，有

应用Burkholder-Davis-Gundy不等式，得

及

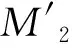
所以

由引理3可得

应用Gronwall 不等式，有

其中：

再由引理1可得

证毕。

由引理1～3及定理1，容易推得下述定理2成立。

定理2 若条件①～④成立，则方程(1)的Euler数值方法在均方意义下是指数稳定的。

4 结束语

本文讨论了一种带Poisson跳的役龄相关随机资本系统数值解的指数稳定性。分析结果表明在给定条件下，系统(1)的Euler数值逼近解在均方意义下是指数稳定的。

[1] FEICHTINGER G,HARTL R F,KORT P M,et al.Anticipation effects of technological progress on capital accumulation:a vintage capital approach[J].Journal of Economic Theory,2006,126:143-164.

[2] FEICHTINGER G,HARTL R F,KORT P M,et al.Capital accumulation under technological progress and learning:A vintage capital approach[J].European Journal of Operational Research,2006,172:293-310.

[3] GOETZ R U,HRITONENKO N.The optimal economic lifetime of vintage capital in the presence of operating costs,technological progress,and learning[J].Journal of Economic Dynamics Control,2008,32:3032-3053.

[4] ZHANG Q M.Convergence of numerical solutions for a class of stochastic age-dependent capital system with Markovian switching[J].Economic Modelling,2011,28:1195-1201.

[5] MATITON M.Jump Linear Systems in Automatic Control [M].New York:Marcel Dekker,1990.

[6] LI R H,HOU Y M.Convergence and stability of numerical solutions to SDDE with Markovian Switching[J].Applied Mathematics and Computation,2006,175:1080-1091.

[7] PANG W K,LI R H,LIU M.Exponential stability of numerical solutions to stochastic age-dependent population equations[J].Applied Mathematics and Computation,2006,183:152-159.

[8] WANG L S,XUE H.Convergence of numerical solutions to stochastic differential delay equations with Markovian switching and Poisson jump[J].Applied Mathematics and Computation，2007,188:1161-1172.

[9] WANG L S,WANG X J.Convergence of the semi-implicit Euler method for stochastic age-dependent population equations with Poisson jumps[J].Applied Mathematical Modelling,2010,34:2034-2043.

[10] RATHINASAMY A.Split-step-methods for stochastic age-dependent population equations with Markovian switching[J].Nonlinear Analysis:Real World Applications,2012,13:1334-1345.

[11] DING X H,MA Q,ZHANG L.Convergence and stability of the split-step-method for stochastic differential equations[J].Computers & Mathematics with Applications,2010,60:1310-1321.

[12] CUI J,YAN L,SUN X.Exponential stability for neutral stochastic partial differential equations with delays and Poisson jumps[J].Statistics & Probability Letters,2011,81:1970-1977.

[13] 徐丽丽.带Poisson跳的非线性随机延迟微分方程数值算法的稳定性分析[D].黄石：湖北师范大学,2015.

[14] ZHANG Q M.Exponential stability of numerical solutions to a stochastic age-structured population system with diffusion[J].Journal of Computational and Applied Mathematics,2008,220:22-33.

[15] ZHANG Q M,RATHINASAMY A.Convergence of numerical solutions for a class of stochastic age-dependent capital system with random jump magnitudes[J].Applied Mathematics and Computation,2013,219:7297-7305.

[16] 杨洪福,张启敏.具有Markov调制的随机年龄结构种群系统半驯服Euler法的指数稳定性[J].数学年刊A辑(中文版),2016,37:7-88.

[17] ZHANG Q M,LIU W A,NIE Z K.Existence,uniqueness and exponential stability for stochastic age-dependent population[J].Applied Mathematics and Computation,2004,154:183-201.

[18] WANG Z P.Stability of solution to a class of investment system[J].Applied Mathematics and Computation,2009,207:340-345.

(责任编辑何杰玲)

StabilityofNumericalSolutionforStochasticCapitalSystemwithPoissonJumps

ZHENG Laiyun

(School of Mechanical Engineering, Ningxia University, Yinchuan 750021, China)

stochastic capital system; numerical solution; Poisson jump; stability

2017-04-15

宁夏自然科学基金资助项目(NZ14048,NZ16005)；宁夏高校科研项目(NGY16061)

郑来运(1979—)，女，宁夏人，讲师，主要从事运筹学与控制理论的研究，E-mail:zhenglaiyun@126.com。

郑来运.带Poisson跳随机资本系统数值解的稳定性[J].重庆理工大学学报(自然科学)，2017(10):222-228.

formatZHENG Laiyun.Stability of Numerical Solution for Stochastic Capital System with Poisson Jumps[J].Journal of Chongqing University of Technology(Natural Science)，2017(10):222-228.

10.3969/j.issn.1674-8425(z).2017.10.036

O231

A

1674-8425(2017)10-0222-07