响应变量缺失下变系数部分线性模型的参数估计

欧玉莲，袁永生，李 磊

(河海大学 理学院，南京 210098)

响应变量缺失下变系数部分线性模型的参数估计

欧玉莲，袁永生，李 磊

(河海大学 理学院，南京 210098)

基于两步法思想，对响应变量随机缺失下的变系数部分线性模型中的参数进行了估计，并通过模拟证明了改进后的两步法对此类问题的解决是简单有效的。实例分析了矮抗58小麦乳熟期抗倒伏情况。实例分析表明：对于小麦的抗倒伏性研究有一定的指导意义，说明了所提方法的合理性与可行性。

缺失数据；变系数部分线性模型；两步法

1 背景

通常情况下，实验终止、数据遗漏等各种人为及偶然因素均会导致数据缺失，这就使得对于数据缺失的处理变得十分关键。因此，对缺失数据的研究已成为统计学的一个热点问题,并取得了一定的研究成果[1-3]。其中，响应变量缺失的情况更为常见，如杨宜平等[4]考虑响应变量存在缺失时部分线性模型的经验似然推断，给出了参数部分与函数部分的置信域和逐点置信区间。赵培信[5]研究了响应变量缺失下变系数部分线性模型的经验似然估计，有效克服了在纵向数据中构造经验似然比函数面临的困难。赵丽棉等[6]考虑响应变量随机缺失下的变系数部分线性模型，给出了参数分量的置信域，证明了其渐近服从标准卡方分布。

纵观以上研究，关于响应变量随机缺失的变系数部分线性模型的研究大都停留在对模型中参数分量的估计及其性质的讨论，而且在估计参数时对于系数函数部分要求2阶可微，而这在实际生活中往往很难满足。本文放宽了2阶可微这一条件，在条件期望存在时，使用多变量下的两步法，考虑变系数部分线性模型，估计出模型中的参数部分与非参数部分，并通过模拟证明与实例分析，进一步说明了该两步法在此种情况下使用的合理性，有一定的推广意义。

2 估计方法

对于变系数部分线性模型，其一般形式为

Y=XTβ+ZTV(T)+ε

(1)

其中：Y是响应变量；X，Z以及T是协变量；β=(β1,β2, …,βp)T是p×1维的未知参数向量；V(·)=(V1(·),V2(·),…Vq(·))T是q×1维未知函数；ε是随机误差项,且ε与协变量间(X,Z,T)不相关，即E(ε|X,Z,T)=0，其中为了避免维数灾害问题，通常假定T为单变量。

假设{(Yi,Xi,Zi,Ti),i=1,2,…，n}是来自模型(1)的一个不完全随机样本，它们独立同分布。

(2)

这里的{(Xi,Zi,Ti)}是可以观测到的数据集，但Yi是存在随机缺失的。引入关于Yi的缺失指示函数δi，当δi=1时，Yi是可以获取的；δi=0时，Yi是缺失的。在此假定Yi随机缺失，固有

P(δi=1|Yi,Xi,Zi,Ti)=

P(δi=1|Xi,Zi,Ti)=π(Xi,Zi,Ti)

(3)

式(3)暗含在给定Xi,Zi,Ti的情况下，δi与Yi是独立的，即缺失的概率只与能完全观测的部分有关，而与存在缺失的部分无关。该假定是统计分析中常用的，且在实际应用中也是合理的。下面对响应变量缺失的情况进行讨论。

将式(2)左右两边同时乘以示性函数δi，则有

i=1,2,…,n

(4)

类似地，采用两步估计法，取关于Z，T的条件期望，可以得到

E(δiYi|Z=z,T=t)=

E(δiXi|Z=z,T=t)Tβ+

E(δi|Z=z,T=t)ZTV(T),

i=1,2,…,n

(5)

将式(5)左右两边同时除以E(δi|Z=z,T=t)，有

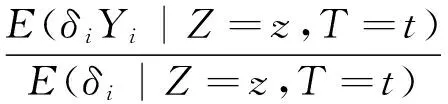
i=1,2,…,n

(6)

对式(6)进行简化，有

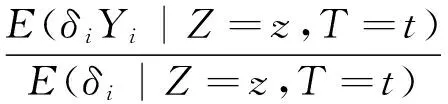
i=1,2,…,n

(7)

从而有

V(T)=V1(T)-V2(T)β

(8)

其中：

V1(T)=(ZZT)-1·Z·g1(Z,T)

V2(T)=(ZZT)-1·Z·g2(Z,T)

(9)

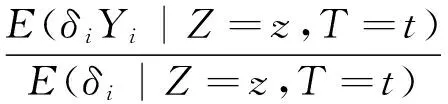
(10)

根据文献[7]可对参数β进行估计，有

(11)

对V1(T)和V2(T)进行估计时，需得到g1(z,t)和g2(z,t)的估计，可考虑使用多变量核函数对其进行估计。因X，Z相互独立，则有Kh1,h2(z,t)=Kh1(z,t)·Kh2(z,t)。

从而有

(12)

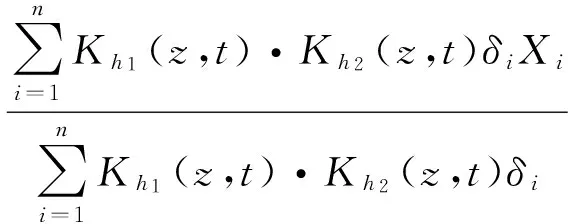
(13)

其中：Khi(·)=K(·/hi)/hi，K(·)为核函数，hi,i=1,2分别对应窗宽。

3 模拟研究

本节通过数据模拟研究所提方法在有限样本下的表现，考虑如下半参数变系数部分线性模型：

Y=3X1+2X2+1.5X3+Z·V(T)+ε

(14)

数据产生如下:

在表1中给出了在两步法下参数β估计的绝对偏差的平均值、标准差及均方误差。

对于参数β的估计，从表1可以得到如下结论：1)对给定的缺失概率，随着样本量的增加，估计量的偏差虽有所波动，但总体趋势在减小，且绝对误差与均方误差都极小；2)对给定样本，随着缺失比例的增加，该估计方法给出的估计量的绝对偏差、标准差和均方误差均有所增加；3)即使是样本个数比较小时，缺失概率有所增加，但参数估计的偏差、标准差以及均方误差都很小，说明该法下估计的参数结果精良。

表1 两步法下参数估计的偏差(Bias)、标准差(SD)和均方误差(MSE)

续表(表1)

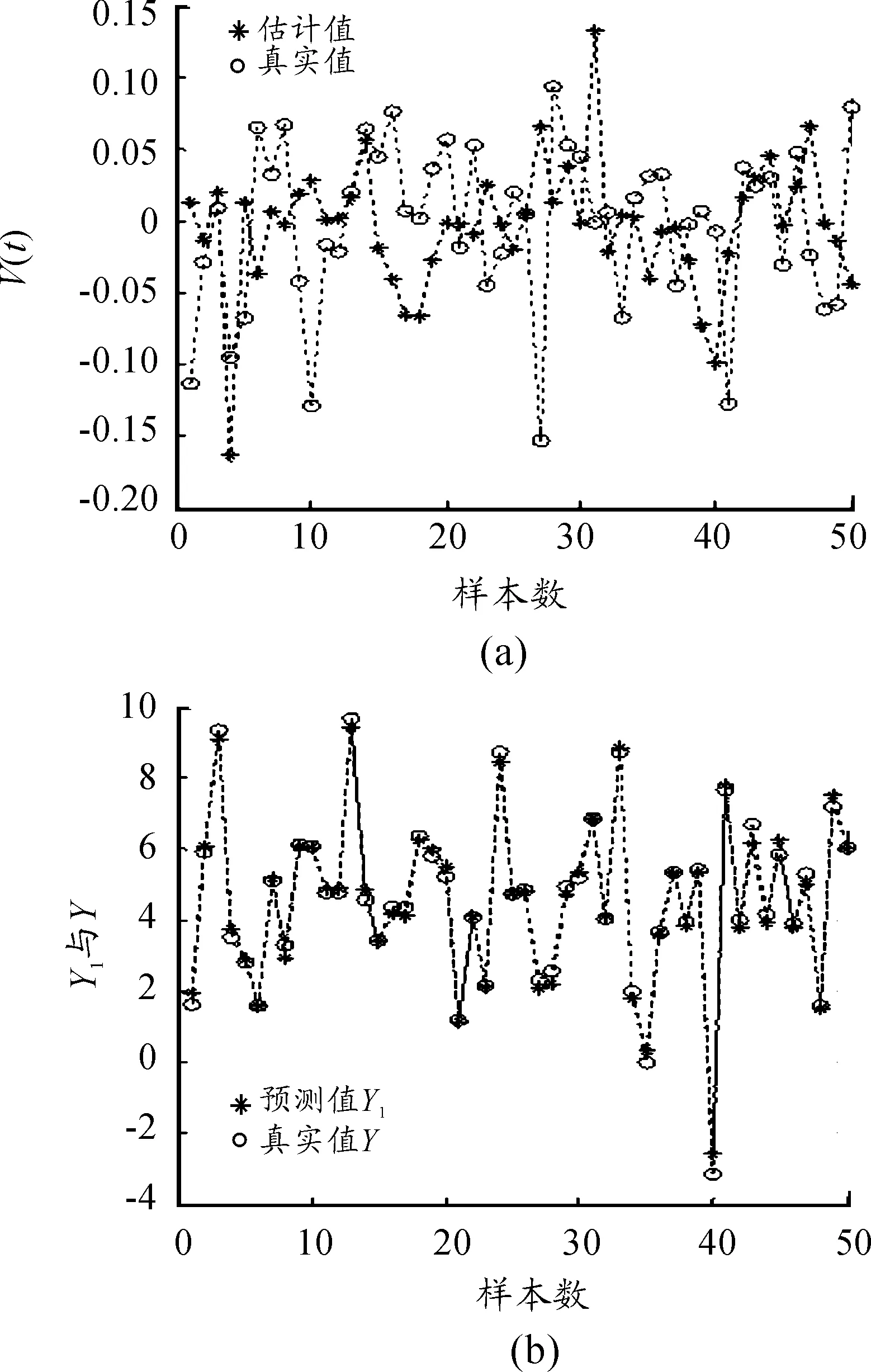
图1 系数函数估计(a)、函数值估计(b)

对于非参数函数部分的估计，从图1(a)可以看出：估计的系数函数与真实函数虽有一定的误差，但除去部分异常点，估计的整体效果良好，误差在±0.2内波动。此外，由图1(b)可以看出：即使非参数部分的估计存在误差，但对函数预测的影响极小，也进一步说明了该种方法的合理性。

4 实例分析

由文献[11]可知：小麦的抗倒伏指数与自身的各指标间可建立一个半参数变系数模型，对于完整数据集假设响应变量存在随机缺失，并利用本文所提的方法做相应的参数估计，结果表明该方法可有效预测小麦的抗倒伏性指数，这对提高小麦的产量研究有一定帮助。

本文选取2007 年矮抗58品种小麦的几个不同时期生理指标作为研究对象，包括小麦各节长度、粗度，单个小麦的重心高度、茎秆壁厚、穗重等对小麦抗倒伏性研究较为重要的指标。具体数据见2011年数学建模中的c题中有关矮抗58 乳熟期数据。因机械强度是衡量小麦抗倒伏性的重要指标,故在此规定机械强度为响应变量，而其他的11个变量均为影响小麦抗倒伏性的重要因素。因其之间具有很强的相关性，因此通过因子分析对其进行降维处理。由spss的输出结果可知，前3个成分的累积贡献率可达76.369%，故在此主成分个数设置为3，取这3个主成分进行分析。通过绘制Y与这3个主成分之间的散点图知，小麦机械强度与第1成分有较为明显的线性关系，而与第2、3 成分没有具体的函数形式，故对影响小麦抗倒伏因素的3个主成分与小麦的机械强度之间建立半参数变系数模型是合理的。

首先，建立模型为Y=Xβ+Z·V(T)+ε。其中：响应变量Y代表小麦机械强度；X代表第1主成分，即F1、Z、T分别代表第2、3主成分(F2,F3)。样本数n=20较小，假定缺失概率为0.1，由模拟中随机产生δ；再使用本文所提到的两步法做参数估计，并利用估计的结果对Y进行预测。

图2 函数预测值

由图2可知：响应变量存在缺失数据情况下的改进两步法估计(*)与完全数据下估计(o)的大部分估计值符合实际情况。对于一些突出的点，可能与源数据存在奇异情况有关，可忽略。以上实例很好地说明了在半参数变系数部分线性模型的协变量缺失数据的情况下，改进的两步法在保证一定的精确度时使用起来更为简单。

5 结束语

基于半参数变系数部分线性模型，考虑了响应变量存在数据缺失的情况，同时放宽对未知函数部分2阶可微的条件限制，使用多变量下的两步法对其中的参数部分及函数部分进行了估计。在保证参数估计精度的前提下，本文算法较以往的方法更为简单，且适用面更广。存在的不足是对未知函数的估计不是很稳定，不过这对最终函数值的预测影响并不大。最后通过模拟验证与实例分析矮抗58小麦乳熟期的机械强度与其自身影响因素的关系，对于今后小麦的抗倒伏性研究有一定的指导意义。采用的实例较好地说明了这种改进两步法的可行性与实用性。

[1] 方匡南，谢邦昌.基于聚类关联规则的缺失数据处理研究[J].统计研究，2011(2)：87-92.

[2] 于力超,金勇进.含非随机缺失数据的面板数据参数估计方法[J].统计研究，2016(1):95-102.

[3] 庞新生.缺失数据处理中相关问题的探讨[J].统计与信息论坛,2004(5):29-32.

[4] 杨宜平,薛留根,程维虎.响应变量存在缺失时部分线性模型的经验似然推断[J].高校应用数学学报A辑,2010(1):43-52.

[5] 赵培信.半参数变系数部分线性模型的统计推断[J].中国科学：数学，2013(7)：635-646.

[6] 赵丽棉,赵培信.响应变量随机缺失下变系数部分线性模型的借补经验似然推断[J].应用数学,2011(2):2.

[7] WANG Q H,LINTON O，HÖDLE W.Semiparametric regression analysis with missing response at random[J].Journal of the American Statistical Association,2004,466:334-345.

[8] 刘远龙.核密度估计中的窗宽选择方法[D].合肥：中国科学技术大学，2013.

[9] WANG Q H,SUN Z H.Estimation in partially linear models with missing responses at random[J].J Multiva-riate Anal,2007,98:1470-1493.

[10] 赵培信,薛留根.响应变量随机缺失下的变系数部分线性模型的经验似然推断[J].工程数学学报,2010(5):771-780.

[11] 刘锋，王利兵，徐振枢.基于半参数变系数部分线性模型的小麦抗倒伏性分析 [J].重庆理工大学学报(自然科学),2013,27(4):121-126.

(责任编辑杨黎丽)

ParameterEstimationforVaryingCoefficientPartiallyLinearModelwithMissingData

OU Yulian, YUAN Yongsheng， LI Lei

(School of Science, Hohai University, Nanjing 210098, China)

The modified two-step method is used to estimate the parametric and nonparametric components and the simulation results show that the improved two-step method is used well to the problem of the absence of response variables in partially linear models. In the end, we analyzed the relationship between the mechanical strength and the other effects of Aikang 58 wheat in the milk stage, which has a certain guiding significance to the research on Lodging resistance of wheat, and it also illustrates the rationality and feasibility of the proposed method.

missing data; semiparametric varying coefficient partially linear model; improved two-step method

2017-02-26

国家自然科学基金资助项目(11201116)

欧玉莲(1993—)，女，硕士研究生，主要从事统计学研究，E-mail: 790547365@qq.com。

欧玉莲，袁永生，李磊.响应变量缺失下变系数部分线性模型的参数估计[J].重庆理工大学学报(自然科学)，2017(10):211-215.

formatOU Yulian,YUAN Yongsheng，LI Lei.Parameter Estimation for Varying Coefficient Partially Linear Model with Missing Data[J].Journal of Chongqing University of Technology(Natural Science)，2017(10):211-215.

10.3969/j.issn.1674-8425(z).2017.10.034

O212.7

A

1674-8425(2017)10-0211-05