热声载荷作用下金属薄壁结构的振动响应与试验验证
沙云东, 王 建, 骆 丽, 赵奉同, 贾秋月
(沈阳航空航天大学 辽宁省航空推进系统先进测试技术重点实验室, 沈阳 110136)
热声载荷作用下金属薄壁结构的振动响应与试验验证
沙云东, 王 建, 骆 丽, 赵奉同, 贾秋月
(沈阳航空航天大学 辽宁省航空推进系统先进测试技术重点实验室, 沈阳 110136)
针对航空航天薄壁结构在热声载荷作用下的非线性振动响应问题,基于声振耦合理论,采用耦合的有限元/边界元法对四边固支高温合金矩形薄壁结构进行了动力学响应计算。重点研究了薄壁结构在行波加载与扩散场加载条件下的振动应力/应变响应规律,讨论了温升对结构振动响应的影响规律,分析了薄壁结构热屈曲(Thermal-buckling)和跳变(Snap-through)响应特性。通过将薄壁结构在不同温度条件下的振动模态以及动态应变响应的仿真结果与热环境下的声激振试验结果进行对比,表明计算的基频量值及随温度的变化关系与试验结果获得较好的一致性,计算的应变响应与试验测试结果量值相当,验证了热声响应计算方法与模型的有效性。该研究提出的金属薄壁结构在热声载荷作用下的非线性振动响应计算方法及分析结论对进一步开展热声疲劳寿命预测及动强度设计提供依据。
金属薄壁结构;热声载荷;非线性振动响应;试验验证
航空航天飞行器具有典型的受热声载荷同时作用的薄壁结构,高温载荷、强噪声载荷和机械力载荷会使结构产生高频振动应力。同时,高温强噪声所引起的大挠度非线性振动响应,使薄壁结构发生过早疲劳失效。为满足高超飞行器、大负荷发动机的结构设计要求,开展热声环境下航空薄壁结构的预研工作显得尤为重要。
为了给航空薄壁结构的热声试验提供大量的参考数据,以提高试验的合理性与可靠性,预先对结构进行仿真计算成为关键。目前用于解决结构非线性响应的解析方法和数值方法主要包含:摄动法、FPK方程法、Von Karman-Herrmann 大挠度板方程、等价线性化方法(EL)、降阶模型法(ROM)、伽辽金法(Galerkin),以及有限元法(FEM)。Lee等[1-3]使用EL法计算了热屈曲板的应力和应变响应。Vaicaitis等[4-5]使用Galerkin法结合Monte Carlo法研究了金属与复合材料结构在随机激励下的非线性响应问题。Lee等[6-8]使用Galerkin法和EL法得到了热声载荷下结构响应统计参数。Mei等[9-10]使用有限元法计算了热声激励下板壳结构的非线性随机响应。同时,针对航空航天薄壁结构热声响应及疲劳问题,国外学者以及研究机构对薄壁板壳,尤其以四边固支矩形薄板为主要试验件做了大量试验研究。NASA Langley研究中心和美国空军Wright-Patterson飞行动力学实验室(AFFDL)[11]为研究热声载荷下薄壁板结构的响应特征,采用行波管对铝板进行了热声试验。Rizzi[12]针对热噪声问题,阐述了动态响应测试方法、高温声疲劳试验方法等。Ng等[13-15]开展了热声载荷作用下四边固支金属板与复材板的非线性响应分析试验,结合单模态方程并获得响应特性规律。Jacobson等[16]为评估适合ASTOVL的复合材料壁板结构,采用行波管,开展了室温和热环境下热噪声试验。Jacobs等[17]采用高温随机疲劳设备和高温行波管研究了陶瓷基复合材料的高温声疲劳性能。
国内沙云东教授所带领的科研团队已经对航空薄壁结构的热声响应与疲劳问题做了大量研究并发表了大量文献[18-23]。例如,在文献[23]中,魏静使用FEM/Galerkin的方法计算四边简支矩形钛合金板在随机激励下的动态响应,分析结构热屈曲现象与非线性跳变响应,并发现热载荷和声载荷对响应非线性特性的影响方式不同:热载荷改变结构刚度特性曲线的形状,屈曲前刚度降低,屈曲后刚度增加;声载荷使得结构工作在刚度曲线的不同区域,强噪声载荷引起的持续跳变使得结构工作在硬化区域,间歇跳变时结构工作在软化区域。
本文在文献[23]的基础上,采用耦合有限元/边界元法[24],对四边固支高温合金矩形薄壁结构进行响应计算,结合结构屈曲与跳变的相关理论研究了声波入射方向、声压级以及温度载荷对结构响应的影响规律,并首次分析了屈曲与跳变状态下应力与应变的响应特性。研究内容对确定合理的疲劳寿命预估模型提供参考,并为高温、强负荷航空航天薄壁结构的动强度设计提供依据。
1 理论基础
1.1 大挠度非线性方程
薄壁结构在强热声载荷下的物理本质已经表现出大挠度强非线性响应。采用Von Karman薄板大挠度理论和Kirchhoff的相关假设,距离中面距离为的任意一点的应变如式(1)所示
(1)
式中:μ,v为中面内位移;w为横向挠度。
对应变位移关系进行微分运算可以得到挠度表示的应变协调方程,如式(2)所示
(2)

(3)
式中:Nx,Ny,Nxy为薄膜力;h为板厚。
将式(3)代入式(2),得到应力函数表示的应变协调方程,如式(4)
(4)
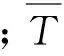

(5)
式中:T(x,y,z)为板上的温度函数分布;θ为板厚的温度梯度。
将应力和对应剪力、薄膜力、弯矩,考虑阻尼力、声载荷、惯性力,对板进行受力分析,可以得到包含温度项的Von Karman大挠度运动方程如式(6)所示

(6)

1.2 边界元法声场控制方程
在声波和固体结构间的交互作用的相关内容中[25],克希霍夫-亥姆霍兹积分方程阐明了某任意物体上表面振动谐运动与周围流体中辐射声压场的关系,它是
(7)

由声波动方程表示的声场控制方程为

(8)
式中:c为声速。设时间步长为eiωt,由声波动方程简化的二维Helmholtz方程为
▽2p+k2p=0
(9)
整个声场内采用边界元法,声场控制方程以矩阵形式表示为
(10)
式中:[H]和[G]为影响矩阵。
其中,ua是边界声场质点位移。将边界条件代入式(10)中,得到边界元法中声场控制方程为
[H]{p}=ρaω2[G]{ua}
(11)
1.3 平板结构动力学控制方程
声压和模态位移之间的关系为
p(x,y,z,t)=Hpactua(t)
(12)
式中:Hpact为声传递函数。声场内任意位置的声压都可由传递函数表示。由边界元法中声场控制方程(10)和方程(11),可以得到一种声传递函数的表达式
{Hpact}=[H-1][G][LT]{-ρaω2}
(13)
施加声载荷谱密度SIN(ω),得到结构模态位移谱密度(Sd(ω))n如下
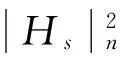
(14)

通过结构表面声质量振动速度等于结构表面振动速度,以考虑声振耦合效应。在频域中将结构有限元与声场边界元的谱密度进行耦合,仅声场边界元的声压谱密度和结构模态位移谱密度为未知量。为了便于表示,可以写为
[CPLG(ω)]{SD(ω)}={SDIN(ω)}
(15)
式(15)中:{SD(ω)}为结构动力学响应谱密度函数;{SDIN(ω)}为外界激励谱密度函数,[CPLG(ω)]为整体耦合矩阵。
式(15)两边乘以[CPLG(ω)]-1,并在频率范围(-ωc<ω<ωc)进行积分,得到

(16)
可以通过简单的梯形近似值法对积分方程(16)进行求解,得到结构模态位移和声场压力谱密度。
2 热声加载仿真计算与分析
仿真计算选用GH188板材,板厚1.5 mm,不同温度下的材料参数如表1所示,边界条件为四边固支,热声载荷加载方式如表2所示。几何模型及危险单元应变提取位置如图1所示。
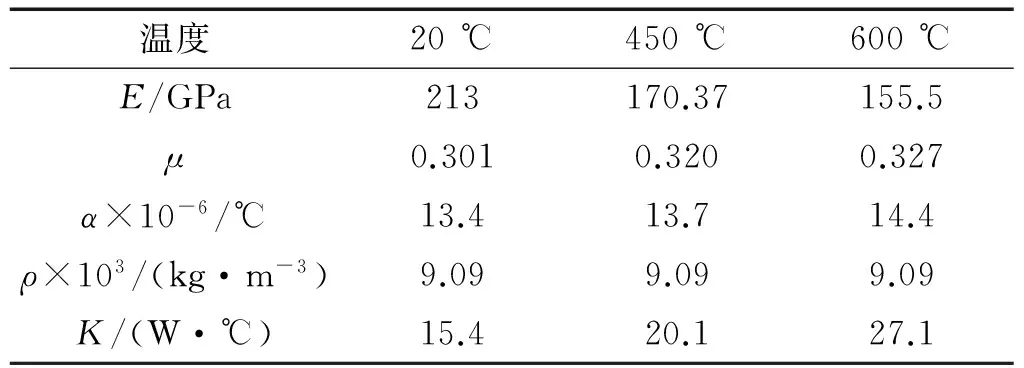
表1 GH188随温度变化的材料参数Tab.1 Material parameters of GH188 in different temperatures

表2 热声载荷加载方式Tab.2 The loading ways of thermal-acoustic
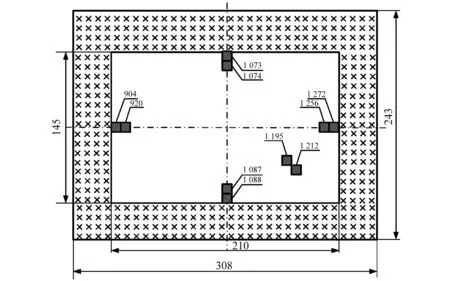
图1 几何模型与应力/应变结果提取单元号Fig.1 The geometry model and unit numbers of stress/strain results extraction
结构在不同温度下的前8阶热模态频率如表3所示。根据结构基频在屈曲前后随温度变化的特征,判断出结构的临界屈曲温度在100 ℃附近。通过仿真计算得出该结构的临界屈曲温度为93.64 ℃。前屈曲时结构处于软化区域,随温度增加刚度降低,基频减小;后屈曲时结构处于硬化区域,随温度增加刚度增加,基频增大。
仿真计算结果表明,温度载荷为50 ℃和100 ℃时结构危险单元为904,温度载荷为150 ℃和200 ℃时结构的危险单元为1 195,温度载荷为250 ℃时结构的危险单元为1 212,如图1所示。将屈曲理论与仿真结果结合分析表明:屈曲前,四边固支薄壁结构的动态响应属于小挠度的线性振动,结构的危险位置一般处于长边/短边中点;屈曲后,大挠度非线性响应使得结构发生失稳,出现局部应力集中,危险点位置随之改变。

表3 四边固支板的前8阶热模态频率Tab.3 The first eight order thermal modal frequencies offour edges clamped plate Hz
2.1 温度与声波入射方向对响应峰值影响规律
当声波入射方向一定且声压级为151 dB时,温度范围为50 ℃~250 ℃,结构产生的振动响应主要集中在结构固有频率附近,尤其在第一阶及低阶共振频率附近具有显著分量,在基频处呈现出最大峰值,如图2所示。
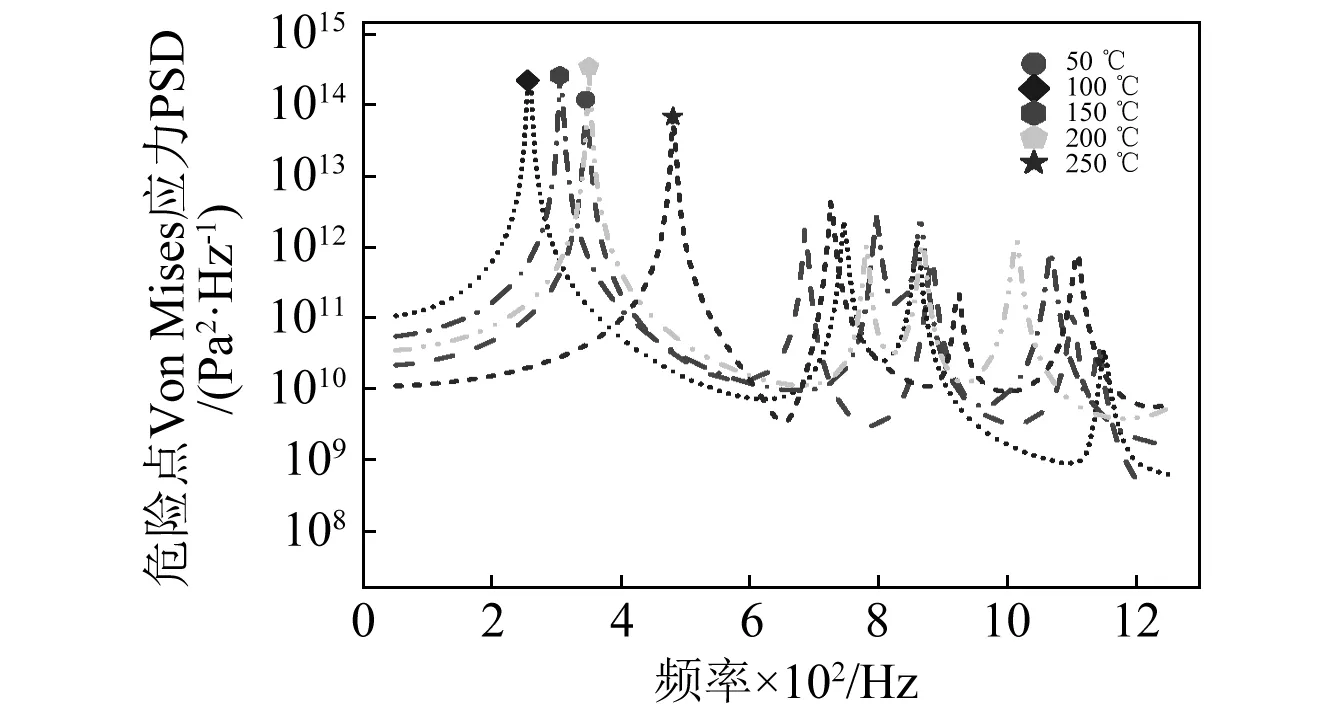
图2 危险位置Von Mises应力PSD随温度变化Fig.2 The Von Mises stress PSD of the dangerous position in different temperatures
分析图2表明:屈曲前结构温度由50 ℃增加到100 ℃时,响应的峰值频率由347 Hz降低到257 Hz,响应峰值由1.2×1014Pa2/Hz增大2.26×1014Pa2/Hz,表明屈曲前结构在高频处出现峰值,随温度的增加,温度所产生的热应力使得结构软化,基频降低,基频处的峰值变大。屈曲后结构温度由100 ℃增加到200 ℃时,此温度段内结构在151 dB作用下声载荷较热载荷强,响应峰值频率由257 Hz增大到350 Hz,响应峰值由2.26×1014Pa2/Hz增大3.56×1014Pa2/Hz,表明屈曲后声压波动载荷占据主导时,结构处于硬化区域,基频升高,基频处的应力响应峰值增大。屈曲后随着结构温度持续的增加由200 ℃增加到250 ℃时,响应峰值频率由350 Hz增大到481 Hz,响应峰值由3.56×1014Pa2/Hz降低到了6.98×1013Pa2/Hz,表明屈曲后随温度继续增加结构处于软化区域,基频处的应力响应峰值减小。
分析图3表明:在温度为100 ℃且声压级为151 dB时,声载荷以具有确定声波入射方向的行波加载,声波与结构之间的交互作用充分,大部分的声能量被结构所吸收,结构的响应明显,一阶响应峰值较大,图中行波加载时结构的响应峰值为2.65×1015Pa2/Hz。当声载荷以具有不确定声波入射方向的扩散场加载时,声波作用到结构以后存在多方向的能量传递,但是在声能量传递过程中分散性加强,故结构的动响应较行波加载弱,图中行波加载时结构的响应峰值为2.26×1014Pa2/Hz。由于声波入射的方向性对结构的响应水平差异明显,基频处响应峰值的数量级不同,故声波入射的方向性在很大程度上决定着结构响应强弱。
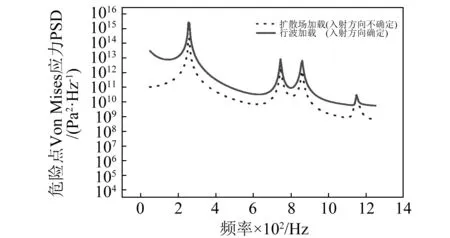
图3 不同声加载方式下危险位置处Von Mises应力PSDFig.3 The Von Mises stress PSD of the dangerous position in different acoustic loading ways
2.2 振动响应随声压级变化规律
研究表明,热声载荷作用下结构在基频处的响应与次阶响应相比要高出约1~3个数量级,结构的响应由一阶响应占据主导,故主要提取结构危险单元在基频处的响应数据以做结构应力/应变响应随声压级变化的规律性分析,后文有关内容的规律性分析与此处类似将不再赘述。
当温度为100 ℃时,研究不同声波入射方向下结构振动响应随声压级变化的规律。由图4和图5研究表明,不同声加载方式下,随声压级增加,结构应力/应变响应的变化趋势一致。148 dB之前,随声压级的增加,结构的应力/应变响应近似线性增加趋势;148 dB以后,热屈曲以及强噪声载荷使得结构呈现大挠度非线性响应,应力/应变响应增幅随声压级增大而增大,且呈抛物线上升趋势。


图4 VonMises应力随声压级变化(a)X向应变随声压级变化趋势(b)Y向应变随声压级变化趋势Fig.4TheVonMisesstresschangeswith图5 不同声加载方式下单向应变值theincreaseofSPLFig.5Unidirectionalstrainunderdifferentacousticloadingways
2.3 应力/应变随温度变化规律
提取结构危险单元在基频处的响应峰值作为分析对象。固定声压级为151 dB不变时,对于两种不同的声波入射方式,结构应力随温度增加都在整体上呈现出先增大后减小的趋势,但是应力响应峰值所对应的温度不同,行波加载与扩散场加载的应力响应峰值所对应温度分别在100 ℃、200 ℃附近,如图6(a)和7(a)所示。表明结构振动的应力响应对声载荷加载方式具有很强的敏感性,特别是声波方向性在很大程度上影响着结构的应力响应强弱。对于具有确定声波入射方向的行波加载,温度载荷为100 ℃时结构在屈曲附近进入跳变区域,应力响应达到最大,如图6(a)所示;而没有确定声波加载方向的扩散场加载时,尽管结构进入了跳变区域,由于声波方向的不确定性导致声能量分散,应力响应峰值发生偏移,在屈曲后的某个温度出现响应的峰值,如图7(a)中结构在200 ℃附近出应力响应峰值。
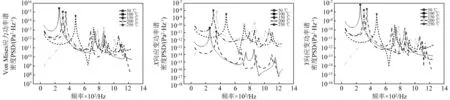
(a)Von Mises应力随温度变化 (b)X向应变随温度变化 (c)Y向应变随温度变化图6 危险单元应力/应变随温度变化趋势(行波加载)Fig.6 The change trend of dangerous unit stress/strain in different temperatures(Progressive wave)
相同声加载方式下,行波加载时,X向和Y向应变都呈现出先增大后减小的趋势,但是X向与Y向应变峰值所对应的温度不同,分别为150 ℃、100 ℃,如图6(b)和(c)所示;这表明行波加载时,结构在屈曲附近的Y向应变远高于X向应变,应力响应主要由Y向应变主导,如图6(a)和(c)所示。扩散场加载时,X向和Y向应变随温度的变化规律不一致,X向应变随温度增加呈现先增大后减小的趋势,Y向应变随温度增加呈现增大-减小-增大-减小的趋势,如图7(b)和(c)所示,这表明扩散场加载时,结构的应变响应对温度更敏感。分析可得,具有确定声波入射方向的行波加载时,结构在屈曲后进入跳变区域会直接激起Y向应变响应作为影响应力响应的主导因素;而没有确定声波入射方向的扩散场加载时,结构的应力响应由不同方向的应变响应共同作用影响。

(a)Von Mises应力随温度变化 (b)X向应变随温度变化 (c)Y向应变随温度变化图7 危险单元应力/应变随温度变化趋势(扩散场加载)Fig.7 The change trend of dangerous unit stress/strain in different temperatures(Diffuse acoustic field)
3 振动响应试验验证
为了对仿真结果与分析结论进行试验验证,针对本文所研究的内容开展了GH188板材构件在热环境下的声激励试验。试验件实际尺寸以及应变片贴片位置如图8所示,测取短边中点X向应变(#1,#3),长边中点Y向应变(#2,#4),试验件现场安装位置与应变片粘贴位置如图9所示。

图8 GH188试验件实际尺寸以及具体的贴片位置Fig.8 Actual size and exact patch location of GH188 test piece

图9 应变片位置以及GH188试验件安装位置Fig.9 Location of strain gauge and the installation location of GH188 test pieces
通过一个口框夹具与双排拧紧螺栓对试验件的四周进行压紧处理,以实现四边固支的约束条件。在将试验件安装在行波管的过程中,要求试验件法线方向与行波加载方向垂直。采用石英灯管布置在试验件的两侧,对其进行双面非对称受热,并在试验件两侧同一位置点处焊接热电偶对试验件表面温度进行监测,如图9所示。在行波管上壁面中心位置安装一个探管式传声器,随机噪声使用高声强噪声试验控制系统进行单点闭环控制,最终实现对试验件的单面受声加载。
热声加载方式如表4所示。试验主要提取试验件在高温、强噪声下的应变响应、加速度响应等数据以分析结构在不同温度下的热模态频率,并为仿真结果的验证分析提供数据支撑。

表4 热声载荷组合Tab.4 The thermal-acoustic loading combinations
分析各个状态下不同贴片位置的应变频谱和加速度频谱,得出构件在不同温度下的一阶共振频率,如表5所示,并将仿真计算的固有频率与试验测得的响应频率进行对比验证,结果表明仿真结果与试验结果具有一致性,如表6所示。同时也验证了结构在屈曲前后基频随温度的变化特征,如图10所示,即屈曲前结构基频随温度升高而减小,例如结构温度由50 ℃增加到100 ℃时,结构基频由347 Hz降低到262 Hz;屈曲后结构基频随温度升高而增大,例如结构温度由150 ℃增加到250 ℃时,结构基频由306 Hz增加到482 Hz。屈曲前测点1位置具有代表性的应变响应频谱,如图11所示。

表5 各测点位置处应变响应的第一阶峰值频率Tab.5 The first order peak frequency of strain response indifferent points Hz

表6 不同温度下GH188试验件一阶固有频率Tab.6 The first-order natural frequency of GH188 test piecesunder different temperatures Hz
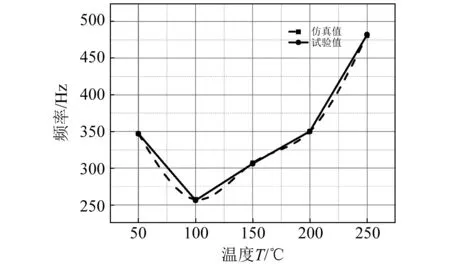
图10 结构响应频率随温度的变化特征Fig.10 The characteristic of structure response frequency with the change of temperature

(a)#1(T=50 ℃,SPL=151 dB)
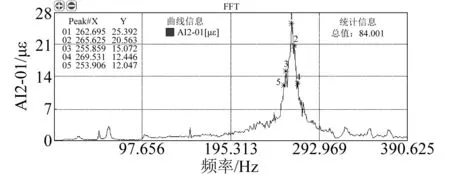
(b)#1(T=100 ℃,SPL=151 dB)图11 试验件应变频域响应结果Fig.11 The strain frequency domain response results
提取长边中点和短边中点的应变结果与试验结果进行对比验证,如表7和表8所示。分析表中数据发现,仿真值与试验值均在一个数量级上,数据吻合性很好。50 ℃时,短边中点试验值和仿真值分别为10.7 με和8.3 με,长边中点的试验值与仿真值分别为13.9 με和12.4 με;100 ℃时,短边中点试验值和仿真值分别为25.4 με和14.9 με,长边中点的试验值与仿真值分别为22.5 με和29.3 με,这表明屈曲前结构处于线性响应阶段,试验值与仿真值表现出高度的一致性。150 ℃时,短边中点试验值和仿真值分别为16.6 με和27.5 με,长边中点的试验值与仿真值分别为26 με和11.1 με,这表明屈曲后大挠度非线性响应使得结构处于非稳定的振动阶段,试验值和仿真值吻合度较屈曲前弱,但是均在一个数量级上。随着屈曲后温度持续增加,在温度为200 ℃与250 ℃时,试验值与仿真值的吻合性再次加强。

表7 短边中点应变仿真值与试验值对比结果Tab.7 The contrast results between simulation value andexperiment value με

表8 长边中点应变仿真值与试验值对比结果Tab.8 The contrast results between simulation value andexperiment value με
4 结 论
(1)采用耦合的有限元/边界元法对四边固支高温合金矩形薄壁结构的热声响应建立了有效的计算方法与模型,计算并确定该结构在不同温度下的危险位置,提取并分析危险位置的响应结果,结果表明该结构的振动响应由基频主导,且声波入射方向性是结构响应的主要影响因素之一。
(2)基于声载荷、声波入射方向性与温度场的变化对结构动力学响应规律的分析,结果表明结构应力/应变响应随声压级增加呈线性增加与大挠度非线性跳变以后的抛物线增加趋势。行波加载时,在温度达到临界屈曲附近时,结构进入跳变区域,应力响应达到最大,会激起某个单向的应变响应作为影响应力响应的主导因素;扩散场加载时,进入跳变区域,应力响应峰值发生偏移,结构单向应变响应对应力响应的作用具有不确定性。
(3)热声试验:验证了仿真中结构一阶固有频率与热声试验中结构一阶响应频率的一致性,且一阶固有频率随温度变化规律相同,结构基频在屈曲前随温度增加而降低,结构基频在屈曲后随温度增加而增大。同时将结构动应变响应的仿真结果与试验结果进行对比,结果表明了仿真计算准确性,验证了四边固支高温合金矩形薄壁结构热声响应计算方法和模型的有效性。
[1] LEE J. Large-amplitude plate vibration in an elevated thermal environment[R]. Flight Dynamics Directorate, Wright Laboratory Wright-Patterson,1992.
[2] LEE J. Displacement and strain histograms of thermally buckled composite plates in random vibration[C]// Structural Dynamics, and Materials Conference and Exhibit, 1996.
[3] LEE J. Displacement and strain statistics of thermally buckled plates[C]// Structural Dynamics, and Materials Conference and Exhibit,1999.
[4] VAICAITIS R. Nonlinear response and sonic fatigue of National Aerospace Space Plane surface panels[J]. Journal of Aircraft, 1994, 31 (1): 10-18.
[5] VAICAITIS R, KAVALLIERATOS P A. Nonlinear response of composite panels to random excitation[C]// Structural Dynamics and Materials Conference,1993.
[6] LEE J. Displacement and strain statistics of thermally buckled plates[C]// Structural Dynamics, and Materials Conference and Exhibit,1999.
[7] LEE J. Displacement and strain histograms of thermally buckled composite plates in random vibration[C]// Structural Dynamics, and Materials Conference and Exhibit, 1996.
[8] LEE J. Large-amplitude plate vibration in an elevated thermal environment [R]. Applied Mechanics Reviews, 1992.
[9] MEI C, DHAINAUT J M, DUAN B, et al. Nonlinear random response of composite panels in an elevated thermal environment [R]. 2000.
[10] DHAINAUT J M, GUO X, MEI C, et al. Nonlinear random response of panels in an elevated thermal-acoustic environment[J]. Journal of Aircraft, 2003, 40(4): 683-691.
[11] NG C F, CLEVENSON S A. High-intensity acoustic tests of a thermally stressed plate[J]. Journal of Aircraft, 1991, 28(4): 275-281.
[12] RIZZI S A. Experimental research activities in dynamic response and sonic fatigue of hypersonic vehicle structures at NASA Langley Research Center[C]// Aerospace Sciences Meeting and Exhibit, 1993.
[13] NG C F. Design guide for predicting nonlinear random response(including snap-through) of buckled plates[M]. Memphis, TN: General Books LLC,2011.
[14] NG C F, WENTZ K R. The prediction and measurement of thermo-acoustic response of plate structures[C]// Structural Dynamics, and Materials Conference,1990.
[15] NG C F. Nonlinear and snap-through responses of curved panels to intense acoustic excitation[J]. Journal of Aircraft, 1989, 26(3): 281-288.
[16] JACOBSON M J. Sonic fatigue of advanced composite panels in thermal environments[J]. Journal of Aircraft, 1983, 20(3): 282-288.
[17] JACOBS J H, GRUENSFELDER C, HEDGECOCK C E. Thermal Acoustic Fatigue of Ceramic Matrix Composite Materials[C]// Structural Dynamics, and Materials Conference,1993.
[18] SHA Y D, GAO Z J, XUE F, et al. Influence of thermal loading on the dynamic response of thin-walled structure under thermo-acoustic loading [J]. Applied Mechanics and Materials, 2011,2/3: 876-881.
[19] SHA Y D, ZHANG Z, ZHAO F T, et al. Estimation of random sonic fatigue life based on peak probability density of Von Mises stress[J]. Advanced Materials Research, 2011,199/200: 913-921.
[20] SHA Y D, LI J Y, GAO Z J. Dynamic response of pre/post buckled thin-walled structure under thermo-acoustic loading[J]. Applied Mechanics and Materials, 2011, 80/81: 536-541.
[21] SHA Y D, GAO Z J, XU F, et al. Influence of thermal loading on the dynamic response of thin-walled structure under thermo-acoustic loading[C]// International Conference on Applied Mechanics, Material and Manufacturing, 2011.
[22] SHA Y D, XU F, GAO Z J. Nonlinear response of carbon-carbon composite panels subjected to thermal-acoustic loadings[J]. Applied Mechanics and Materials, 2012, 117/118/119: 876-881.
[23] 沙云东,魏静,高志军.热声载荷作用下薄壁结构的非线性响应特性[J]. 航空学报, 2013, 34(6): 1336-1346.
SHA Yundong, WEI Jing, GAO Zhijun. Nonlinear characteristics of thin-walled structures under thermo-acoustic loadings [J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(6): 1336-1346.
[24] Pates Carl Stansbbury. Analysis of random structure-acoustic interaction problems using coupled boundary element and finite element methods[D]. Norfolk, VA: Old Dominion University, 1994.
[25] NORTON M P. 工程噪声和振动分析基础[M]. 盛元生, 译. 北京:航空工业出版社,1993.
Vibrationresponsesanalysisandexperimentalverificationofmetallicthin-walledstructurestothermal-acousticloadings
SHA Yundong, WANG Jian, LUO Li, ZHAO Fengtong, JIA Qiuyue
(Liaoning Province Key Laboratory of Advanced Measurement and Test Technology of Aviation Propulsion Systems, Shenyang Aerospace University, Shenyang 110136, China)
For nonlinear vibration response problems of aerospace thin-walled structures under thermal-acoustic excitations, based on the theory of structural-acoustic coupling, the coupled FEM/BEM method was used to calculate dynamic responses of super-alloy thin-wall rectangular plates with four edges clamped. This work mainly focused on the influence of progressive wave and diffused acoustic field on the vibration stress/strain responses of thin-walled structures. the effects of temperature rising on vibration responses of structures were discussed, and the characteristics of thermal-buckling and snap-through of thin-walled structures were analyzed. By comparing simulation results of vibration modals and dynamic strain responses of thin-walled structures in different temperatures with experimental results of thermal-acoustic excitations, it shows that fundamental frequencies and changing trend with the increase of temperature of structures keep a preferable consistency with test results, and strain responses of calculation and experimental results have a good alignment, validating the effectiveness of calculation method and model to thermal-acoustic responses. The calculation method of thin-walled structures nonlinear vibration responses and analysis conclusions presented in this paper provide references to future thermal-acoustic fatigue life prediction and the dynamic strength design of thin-walled structures.
metallic thin-walled structures; thermal-acoustic loads; nonlinear vibration responses; experimental verification
航空基础科学基金资助基金项目(20151554002)
2016-03-09 修改稿收到日期: 2016-09-05
沙云东 男,博士,教授,1966年生
O322
A
10.13465/j.cnki.jvs.2017.20.033

