基于局部偏差的图像分割与偏置场校正模型
黄臣程, 李兆飞
(四川理工学院自动化与信息工程学院,四川自贡643000)
基于局部偏差的图像分割与偏置场校正模型
黄臣程, 李兆飞
(四川理工学院自动化与信息工程学院,四川自贡643000)
利用活动轮廓模型对二维空间上的图像进行分割与偏置场校正,存在对初始曲线的位置敏感、对低对比度图像的分割效果不佳等问题。引入局部偏差矩阵对医学图像数据进行分割与偏置场校正,一方面,通过极小化测量图像与真实图像之间的偏差,使模型能够更加准确地进行分割;另一方面,通过交替迭代的方式计算偏置场,对图像进行校正使得对比度更加合理。对具有不同目标边界形态的合成图像和医学图像进行了实验,结果表明该模型对初始曲线的位置具有较强的鲁棒性,分割结果的准确性和偏置场的修正效果优于其他模型。
图像分割;活动轮廓模型;医学图像;偏置场校正
引言
图像分割是计算机视觉与人工智能中最基本的环节。在医学核磁共振(MR)图像中,由于磁场分布的不均匀性(偏置),导致获得的图像灰度分布不均匀[1]。MR器官图像分割被广泛应用于临床医学诊断。
活动轮廓模型[2](Active Contour Model, ACM)自提出以来受到了很大的关注与研究[3-4]。其主要思想是将图像分割问题转化为求解一个曲线演化方程,并用演化后的曲线表示目标的边缘。ACM通常可以分为两类:基于边界[5-6]和基于区域的模型[7-10]。基于边界的ACM是利用图像的梯度信息来引导曲线朝目标的边界运动,由于利用了梯度信息,这类ACM对含有噪声和弱边界图像的分割效果不佳。基于区域的ACM利用图像目标与背景灰度的统计信息来驱动曲线向目标边缘运动,由于利用了图像的灰度统计信息,其对含有噪声和弱边界的图像分割效果优于基于边界的ACM。
Chan和Vese提出的模型(Chan-Vese, C-V)是经典的基于区域的ACM,但是其通常假设图像中的目标和背景都是具有同质性,即目标和背景的灰度是均匀变化的。对于医学图像而言,图像的灰度通常表现出一定的不均匀性,CV模型对其分割结果不佳。为分割灰度不均匀图像中的目标,Li等[11]提出局部二值化拟合(Local Binary Fitting,LBF)的方法,该方法考虑了图像中每个像素点邻域内的灰度均值情况,引导曲线在图像局部区域内的运动方向,能够很好地分割医学图像中的一些器官。此后,局部化的模型受到了极大的关注与研究[12-15]。
由于医学图像通常含有一定程度的偏置场干扰,需要对图像进行偏置场修正,使得医学图像的目标和背景的灰度分布更加均匀。Li等[16]人利用图像合成模型(Retinex乘性模型)的特点,提出了图像分割与偏置场修正同时进行的活动轮廓模型[17-18],更加有利于医学诊断。但是该方法对初始曲线位置比较敏感,且对灰度差异不大的目标和背景难以得到理想的结果。周震在乘性模型基础上,对图像进行对数变换,将之转化为加性模型[19],亦取得了比较好的分割效果。另外,Zhang等在文献[17-18]基础上提出了基于局部统计的活动轮廓模型[20],该模型利用Bayes公式极大先验概率方法构造相应的模型,考虑图像在局部的方差变化信息,能够提高对图像中目标与背景灰度差异比较小的区域的分割准确性。然而和Li 模型一样,Zhang模型对初始曲线位置也比较敏感,且在具有较小局部方差的区域,会造成计算不稳定,影响分割的准确性和偏置场修正。
上述模型只对单个图像切片进行分割处理,缺乏对切片之间待分割目标的三维空间关联描述,因此,在对三维目标进行分割的时候,不可避免地会带来一定的误差。基于三维医学MR图像数据的处理和分析不仅能够提高分割的可靠性,也能帮助更好地理解医学图像的组织结构信息。
针对二维图像分割模型的缺点,本文提出一种三维医学图像分割与偏置场修正方法,通过引入局部偏差矩阵,度量在图像分割过程中得到的测量值与真实值之间的差异,并通过极小化该度量,使得差异最小化,从而得到较好的图像分割结果和偏置场修正效果。
1 图像分割与偏置场修正模型
1.1 Li模型
在医学MR图像中,由于磁场强度的不均匀分布而使图像受到一定程度的偏置场(灰度不均匀性)影响。为了分割灰度不均匀分布的图像,Li 等考虑了如下的图像合成模型[16]:
I=b·J+n
(1)
其中,I为待测量的图像,b为偏置场(或光照场),J为真实的图像,n为加性噪声。假设真实图像J和偏置场b满足如下两个条件[17-18]:
(A1) 在整个图像区域内,偏置场b是缓慢变化的。
(A2) 真实图像J的灰度在每一个组织(目标)的分类中是接近于常数的,如
为Ω的一个划分)。
利用上面两个假设条件,考虑如下的能量泛函:
(2)
其中,Ωx={y:|y-x|≤ρ}为图像区域中点x的半径为ρ的圆形邻域,Ωx∩Ωi表示由图像的第i个划分Ωi产生的Ωx的划分。Kσ(s)通常选取为具有标准差为σ的截断的Gauss核函数。
由于截断Gauss窗口的引入,Li模型可以在局部考虑图像灰度以及偏置场的分布信息,能够很好地解决强度不均匀性图像的分割问题,同时又能对图像进行偏置场修正。但是,该模型对初始曲线位置比较敏感(图1),且在目标和背景灰度比较接近的地方,容易引导曲线朝着错误的方向演化。ci是加权的全局平均灰度,b是偏置场,它们在模型中交替更新,相互影响,只要ci的计算出现了偏差,b的估计值也会出现偏差,因此Li模型对初始曲线位置的选取比较敏感且对灰度接近的目标和背景容易分割失败。
1.2 Zhang模型
为了克服Li 模型在图像中目标与背景灰度差异比较小的区域的分割准确性,Zhang等[20]通过考虑图像的局部方差,提出了基于灰度分布的活动轮廓模型(简称Zhang模型)。假设图像I(y)在局部区域Ωx∩Ωi上服从Gauss分布:
1,2,...,N
(3)
考虑所有图像区域中的点后,构造一个能量泛函:

(4)
该模型通过对局部区域的方差信息进行收集,能够分割目标与背景灰度比较接近的区域。但是,和Li 模型一样,Zhang模型对初始曲线位置比较敏感,另一方面在具有较小局部方差的区域,可能会造成计算不稳定,而导致分割失败。
2 三维图像分割与偏置场修正模型及实现
在Li模型中,图像的分割与偏置场估计是同时进行的,交替迭代,相互影响。在本文前期的工作中,通过引入局部偏差矩阵来对该模型进行改进[21],以提高模型对医学图像分割和偏置场修正能力。在该工作基础上,本文进一步将前期的工作推广到三维图像,在三维Li模型中引入一个局部偏差三维矩阵数组d,用来修正真实图像体数据和逼近值之间的差异,从而提高分割的准确性和偏置场估计的合理性,进而改善修正图像的视觉效果。对于一个输入图像体数据I(x)(x=(x,y,z)),考虑如下的模型:
I=b·J+d+n
(5)
其中,d为三维偏差数组,描述了图像I与逼近模型b·J在数据局部区域之间的偏差程度。因此在球形区域Ωx可得到局部区域能量泛函:
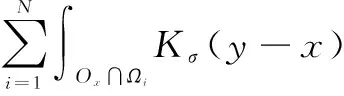
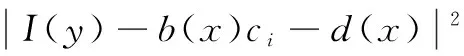
(6)
利用水平集方法[22]表示如下:
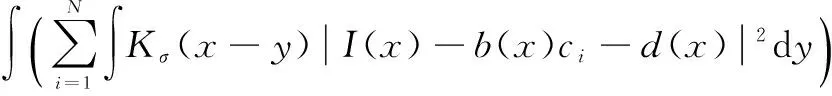
ui(φ(x))dx
(7)
其中,ui(s)为区域Ωi的隶属函数。
为使水平集函数在演化过程中更加光滑,且避免被重新初始化,在模型中加入曲面面积项[8]EL(φ)和一个惩罚项[23]P(φ):
(8)
组成正则化能量如下:

(9)
其中,α,β>0。则能量方程为:
E(b,c,d,φ)=
ui(φ(x))dx+ER(φ)
(10)
固定φ,分别对b,ci(i=1,2,...,N)和d求导,得到极小解:
(11)
在三维空间,活动轮廓演化曲面用水平集函数表示为Γ={(x,y,z)|(x,y,z)∈Ω,φ(x,y,z)=0},用一个或多个水平集函数φ1,φ2,...,φm表示N个三维区域Ωi,i=1,2,...,N的隶属函数Mi:
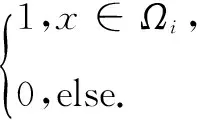
(12)
由隶属函数的定义可以知道,m个水平集函数φ1,φ2,...,φm可以表示N=2m个隶属函数,即N=2m个区域Ω1,Ω2,...,ΩN,将多个水平集函数表示成向量函数的形式Φ=(φ1(x),φ2(x),...,φm(x)),则隶属函数Mi(φ1(x),φ2(x),...,φm(x))可以简化为Mi(Φ)。对于真实图像,主要考虑N=2,3的情况,其他情况可以直接推广。当N=2时,隶属函数为M1(φ)=H(φ)和M2(φ)=1-M1(φ),其中H(φ)为Heaviside函数。当N=3时,隶属函数分别为M1(Φ)=H(φ1)H(φ2),M2(Φ)=H(φ1)(1-H(φ2))和M3(Φ)=1-H(φ1)。
以N=2为例,三维曲面演化方程如下:
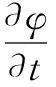
(13)
其中,δε(φ) 为Dirac函数,f1(x)和f2(x)的由如下式子计算:
(14)
用φn表示第t=nΔt时刻的水平集函数值,利用有限差分法,得到式(13)的差分方程:

(15)
对于N=3的情况,可以类似推导。
3 实验结果
本文主要从以下几个方面验证模型的可靠性与准确性:(1)活动轮廓模型对初始位置敏感的问题;(2)对目标与背景灰度差异较小区域的分割效果;(3)对医学MR体数据的分割效果。实验环境基于Windows7 64位平台的Matlab 2011b,硬件条件为Core2 2.4 GHz CPU、4 GB RAM。实验参数如无特殊说明均选取如下:σ=10、ε=1,时间步长Δt=0.1,α=0.1/Δt,β=0.003×255×255。
3.1对初始曲线的鲁棒性
图1给出了三种方法在不同的初始曲线位置时对二维合成图像的分割结果。其中第1列为初始曲线位置,第2列至第4列分别为Li模型、Zhang模型以及本文模型的分割结果、偏置场图像以及偏置校正后的结果。第1行与第4行为三个模型的分割结果,第2行与第5行为经过偏置场校正后的图像,第3行与第6行为三个模型对图像偏置场的估计结果。在二维情况下,当初始曲线位于目标内部时,三个模型得到类似的分割结果,但是本文方法对图像的偏置场校正效果更佳(第2行第4列)。当初始曲线位置包含整个目标的时候,Zhang模型和Li模型的分割结果不是很理想,曲线出现断裂的情况,而本文模型依然能够得到很好的结果(第4列第5行)。图1所示的实验结果表明,本文方法对初始曲线的位置不敏感,对偏置场进行修正的同时可得到较好的分割结果。

图1 三个模型在不同初始曲线位置下的结果
对图1中的合成图像进行叠加得到25层的三维数据。分别用Li模型、Zhang模型和本文的模型对该三维图像进行分割实验。图1第4行的三维分割结果如图2所示,从左至右分别为本文方法、Li模型与Zhang模型的结果。本文模型对初始曲面(初始曲线)的位置具有比较好的鲁棒性,得到的三维分割结果更加准确。

图2 三种方法关于图1第四行结果的三维显示
3.2对低比对图像的分割结果
图3为三个模型对二维强灰度不均匀图像数据中目标(鱼)处理得到的结果比较。可以看出在局部区域内(鱼头部分),目标和背景的灰度几乎一致。第1列至第4列分别为初始曲线位置、图像分割结果,修正后的图像以及偏置场的显示。第1行为Li模型的实验结果,第2行为Zhang模型的实验结果,第3行为本文模型的实验结果。可以看出本文模型与Zhang模型都能得到鱼的轮廓,Li方法对于背景与目标灰度较近的区域分割效果不好,从而影响最终的图像修正。而本文的图像由于考虑了局部偏差,使得演化曲线(曲面)能够很好地处理目标与背景灰度差异不大的区域,且本文的修正图像比其他两个模型具有很好的对比度,能够更加清楚地辨别图中的目标。

图3 三个模型对强灰度不均匀图像的实验结果
3.3三维医学数据的分割结果比较
试验比较了三个模型对181张医学MR序列图像白质的三维分割结果。医学MR序列图像的获取网站为http://www.bic.mni.mcgill.ca/brainweb。为了方便分析与对比,首先对比三个模型对其中两张切片图像的分割结果,如图4所示。图4从上到下分别为原始的MR切片图像(第55、137张)以及其相应白质图。第1列为真实的白质图像,第2列至第4列分别为本文模型、Zhang模型和Li模型的分割结果。可以看出Li模型和Zhang模型在局部均有出现较多的过分割情况,而本文模型能够得到比较好的分割结果。
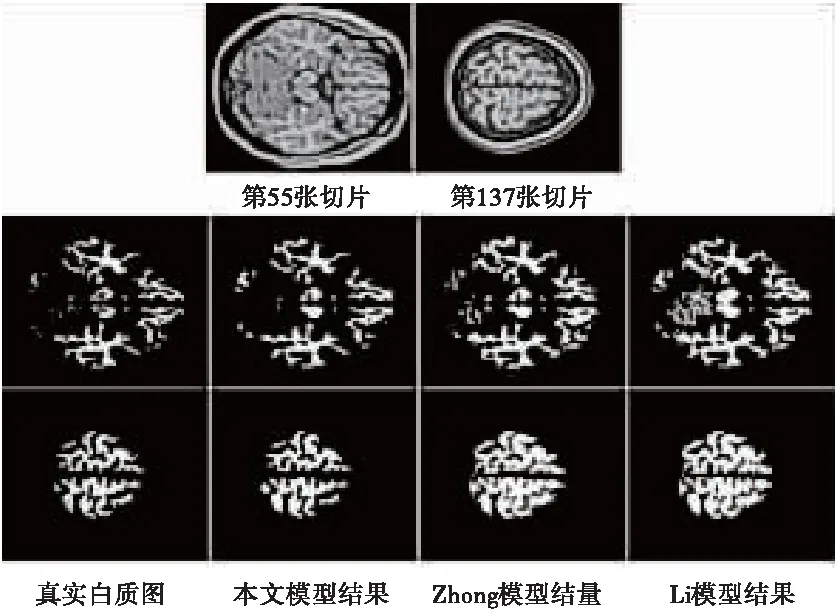
图4 三个模型对第55、137张MR图像的分割结果对比
对181张切片组成的三维数据进行分割,得到两个不同方向的三维显示结果图,如图5所示,第1列为真实白质的显示结果,第2列至第4列分别是Li模型、Zhang模型和本文模型得到的结果。由前节分析可知,本文模型对细节的分割效果优于其它两个模型。如图5所示,本文模型得到的分割结果较其他两个模型更佳。

图5 三个模型对医学MR体数据的分割结果对比
4 结束语
真实图像通常会受到灰度不均匀分布的干扰,现有的图像分割和校正模型中,分割结果的准确性与初始曲面(曲线)的位置紧密相关,同时背景与目标灰度差异较小的区域也会影响图像分割效果,从而影响对图像的校正效果。
本文提出的引入局部偏差数组的模型很好地克服了上述缺点。一方面,通过极小化测量图像与真实图像之间的偏差,使模型能够得到更加准确的进行分割;另一方面,通过交替迭代的方式计算得到的偏置场,通过校正使得图像对比度更加合理。实验表明,这种方法有效地解决了模型对初始位置的敏感性问题,并且能够得到更加准确的分割结果和偏置场修正效果。此方法已经在相关系统中成功应用于三维医学图像的分割与校正。
[1] 田捷.医学影像处理与分析[M].北京:电子工业出版社,2003.
[2] KASS M,WITKIN A,TERZOPOULOS D.Snakes:active contour models[J].International Journal of Computer Vision,1988,1(4):321-331.
[3] CASELLES V,CATTE F,COLL T,et al.A geometric model for active contours in image processing[J].Numerische Mathematik,1993,66(1):1-31.
[4] KICHENASSAMY S,KUMAR A,OLVER P,et al.Gradient flows and geometric active contour models[C]//Proceeding of the 5th International Conference Computer Vision,Cambridge,MA,USA,June 20-23,1995:810-815.
[5] CASELLES V,KIMMEL R,SAPIRO G.Geodesic active contours[J].International Journal of Computer Vision,1997,22(1):61-79.
[6] VASILEVSKIY A,SIDDIQI K.Flux-maximizing geometric flows[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2002,24(12):1565-1578.
[7] TSAI A,YEZZI A,WILLSKY A.Curve evolution implementation of the Mumford-Shah functional for image segmentation,denoising,interpolation,and magni-fication[J].IEEE Transactions on Image Process,2001,10(8):1169-1186.
[8] CHAN T,VESE L.Active contours without edges[J].IEEE Transactions on Image Processing,2001,10(2):266-277.
[9] ZHANG K,ZHANG L,SONG H,et al.Active contours with selective local or global segmentation: a new formulation and level set method[J].Image and Vision Computing,2010,28(4):668-676.
[10] LIU L,ZENG L,LUAN X.3D robust Chan-Vese model for industrial computed tomography volume data segmentation[J].Optics and Lasers in Engineering,2013,51(11):1235-1244.
[11] LI C,KAO C,GORE J,et al.Implicit active contours driven by local binary fitting energy[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition,Minneapolis,MN,USA,June 17-22,2007:1-7.
[12] WANG L,HE L,MISHRA A,et al.Active contours driven by local Gaussian distribution fitting energy[J].Signal Processing,2009,89(12):2435-2447.
[13] DONG F,CHEN Z,WANG J.A new level set method for inhomogeneous image segmentation[J].Image and Vision Computing,2013,31(10):809-822.
[14] LI L,ZENG L,QIU C,et al.Segmentation of computer tomography image using local robust statistics and region-scalable fitting[J].Journal of X-Ray Science and Technology,2012,20(3):255-267.
[15] HUANG C,ZENG L.Robust image segmentation using local robust statistics and correntropy-based K-means clustering[J].Optics and Lasers in Engineering,2015,66:187-203.
[16] LAND E,MCCANN J.Lightness and retinex theory[J].Journal of the Optical Society of America,1971,61(1):1-11.
[17] LI C,HUANG R,DING Z,et al.A variational level set approach to segmentation and bias correction of images with intensity inhomogeneity[J].Med Image Comput Comput Assist Interv,2008,11(2):1083-1091.
[18] LI C,HUANG R,DING Z,et al.A level set method for image segmentation in the presence of intensity inhomogeneities with application to MRI[J].IEEE Transaction on Image Processing,2011,20(7):2007-2016.
[19] 周震.MR图像偏差场校正与分割的研究[D].北京:首都医科大学,2007.
[20] ZHANGK,ZHANG L,LAM K,et al.A local active contour model for image segmentation with intensity inhomogeneity[EB/OLJ].(2013-05-30).https://www.researchgate.net/profile/Kaihua_Zhang4/publication/236965934_A_Local_Active_Contour_Model_for_Image_Segmentation_with_Intensity_Inhomogeneity/links/00b7d53a13847877d2000000/A-Local-Active-Contour-Model-for-Image-Segmentation-with-Intensity-Inhomogeneity.pdf.
[21] HUANG C,ZENG L.An active contour model for the segmentation of images with intensity inhomogeneities and bias field estimation[J].Plos One,2015,10(4):1-24.
[22] OSHER S,FEDKIW R.Level set methods and dynamic implicit surfaces[M].New York: Springer-Verlag, 2002.
[23] LI C,XU C,GUI C,et al.Level set evolution without re-initialization:a new variational formulation[C]//Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition, CVPR 2005,San Diego,CA,USA,June 20-25,2005:430-436.
ActiveContourModelforImageSegmentationandBiasFieldCorrectionBasedonLocalRegionalDifferenceModification
HUANGChencheng,LIZhaofei
(School of Automation and Information Engineering, Sichuan University of Science & Engineering, Zigong 643000, China)
There are some limitations of 2D active contour model for image segmentation and bias field correction such as the sensitivity to initial contours, the unsatisfactory segment result of low contrast image and so on. In this paper, local regional difference for the segmentation and bias field correction of medical images is introduced. For one hand, by minimizing the differences between measured images and true images, more accurate segment results are obtained, for the other hand, the bias field can be calculated by an alternate iterative method, which makes more reasonable for bias field correction of image. Experimental results of our proposed method for some synthetic and medical images with different object show the advantages of our model in terms of robustness to the initial contours, the accuracy of segment results and the results of bias field correction.
image segmentation; active contour; medical image; bias field correction
TP391.41
A
2017-07-20
四川理工学院人才引进项目(2015RC49;2014RC11;2015RC16)
黄臣程(1984-),男,重庆秀山人,博士,主要从事图像处理、偏微分方程等方面的研究,(E-mail)peter1234321@126.com;
李兆飞(1982-),男,副教授,博士,主要从事图像处理和故障诊断与检测等方面的研究,(E-mail)lizhaofei825@163.com
1673-1549(2017)05-0044-07
10.11863/j.suse.2017.05.08

