CNN超混沌系统伪随机序列发生器设计
张琴,林达, 许理
(四川理工学院自动化与信息工程学院, 四川自贡643000)
CNN超混沌系统伪随机序列发生器设计
张琴,林达, 许理
(四川理工学院自动化与信息工程学院, 四川自贡643000)
基于CNN超混沌系统,设计了一种混沌伪随机序列发生器。通过对细胞神经网络系统的理论分析及仿真实验可知,该系统具有复杂的动力学特性,具有初值敏感性、密钥空间大等特点,非常适合作为伪随机序列发生器。基于该系统的发生器能够产生两种不同的序列,一种为二进制序列,另一种为十进制序列,并且通过该发生器产生的伪随机序列具有良好的性能,如序列值的均匀分布性、尖锐的自相关特性和良好的互相关特性。除此之外,利用NIST标准对序列发生器进行性能检验,检验结果表明该序列满足伪随机序列的要求,具有较高的安全性和保密性,具有较好的应用前景。
超混沌;细胞神经网络;伪随机序列发生器
引言
混沌理论在确定性与随机性之间架起了互通的桥梁,是经典力学的一次革命突破[1]。混沌是确定性的非线性动力系统,由于它具有伪随机性、对初值敏感性等特性,使得它非常适合保密通信、信息加密等工程领域[2]。而混沌的应用需要产生混沌信号、混沌序列,而混沌序列的产生需要混沌伪随机序列发生器[3-5]。文献[6]中,Rafik Hamza提出了一种基于陈氏混沌系统的伪随机序列生成算法。文献[7]中,Franois等人提出了一种随机序列产生算法,该随机序列是由混合的三个混沌映射产生的,该序列发生器能够抵抗一些攻击,如差分攻击、穷举攻击。文献[8]中,Hu等人提出了一种基于陈混沌系统的伪随机序列发生器,该系统具有较高的承受攻击的能力。
目前,一些基于混沌系统的加密方案存在一些安全性问题[9-10],主要存在的问题有:密钥空间、算法的构造、一些低维的混沌映射,如文献[11]中提到的一维Logistic映射,在有限精度计算中存在周期退化的问题。事实上,一个复杂的高维混沌映射要比任何低维的混沌映射安全[6],而且复杂的高维混沌系统能提高伪随机序列生成器的安全性。因此,基于高维混沌系统的伪随机序列发生器适合产生密钥流。
1 细胞神经网络(CNN)超混沌系统
细胞神经网络(CNN)的神经元激活函数是非线性函数,因此细胞神经网络是高度非线性动力学系统,四阶CNN系统能够产生超混沌行为。本文所采用的超混沌系统模型为[12]:
(1)
系统(1)的超混沌细胞神经网络的混沌吸引子相图如图1所示,为在Matlab中仿真得到的各个相平面上的混沌吸引子。

图1 超混沌细胞神经网络的吸引子相图
为了能够更直观地看到不同的初值对混沌系统的影响,建立对应值的时间序列图和直方图,如图2~图3所示。图2(a)与图2(b)是x1=1.0对应的时间序列图与直方图;图2(c)与图2(d)是x1=1.0+10-11对应的时间序列图与直方图。图3是x4分别取值4.0与4.0+10-11对应的时间序列图与直方图。从这些图中,可以看出由超混沌细胞神经网络系统直接产生的序列不是均匀分布的。换言之,由超混沌细胞神经网络系统产生的序列不能直接用于图像密码学中,它需要经过适当的量化处理之后才可以使用,常见的量化方法有:二值量化、中间多比特量化等[13-14]。

图2 不同初值时的x1值分布
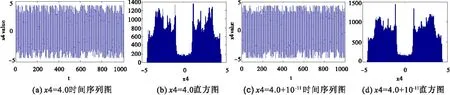
图3 不同初值时x4值分布
2 基于CNN超混沌系统的伪随机序列发生器设计
量化是生成混沌伪随机序列非常重要的一个环节,该环节直接影响生成序列的复杂性和随机性[2]。量化算法的好坏最终会影响到其应用的安全性,随机性是衡量量化算法优劣的主要指标之一,因此选择合适的量化算法是至关重要的。
基于大量的实验,提出了一种量化算法,该算法生成的序列是均匀分布的,并且具有随机统计的特征。该量化算法如下:
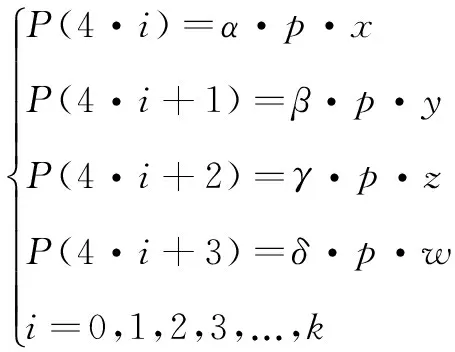
(2)
其中:
(3)
S=round (|P|bmodl)
(4)
其中:round为四舍五入符号,mod为取余符号,S为该算法产生的一维序列。序列S的输出是二进制数还是十进制数,主要取决于l的取值。l的值可以取2或256,当l=2时,序列S为二进制输出,当l=256时,序列S为十进制整数输出。
x(i)、y(i)、z(i)、w(i)为神经细胞网络系统的样本,α、β、γ、δ为样本绝对值之和的平均值,k为轨道x、y、z、w中任意一个的长度,换句话说,假设序列的长度为n,那么k的长度为n的1/4倍。利用公式(2)产生一个长度为n的一维向量序列P,且P为实数。最后,利用公式(4)产生序列S。
具体的伪随机发生器设计步骤如下:
步骤1:选取四阶CNN超混沌系统的初始值及系统控制参数。
步骤2:将初始值及系统控制参数带入CNN系统中,进行多次迭代,产生一系列一定范围内的实数值。
步骤3:产生的实数值不能直接作为伪随机序列,需将这些实数值进行量化处理。
步骤4:将公式(3)带入公式(2)中,利用公式(2)得到4组长度相等的实数值,并将这4组数据按一维行向量排好序。
步骤5:利用公式(4)可以产生两种伪随机序列,当l=2时,产生的S为二值序列,当l=256时,产生的S序列范围为0~255,S序列即为所需要的伪随机序列。
根据上述步骤设计的伪随机序列发生器,相比于一般的二值量化算法,具有较好的伪随机特性,并且基于CNN超混沌系统设计的伪随机发生器产生的序列具有较高的安全性。除此以外,利用该伪随机发生器能够产生两种不同的伪随机序列,一种为二进制序列,另一种为十进制序列,实现一物多用功能。
该量化算法是基于4个混沌轨道坐标的结合,这样可以确保伪随机序列发生器的安全性。该发生器的输入即为密钥,密钥的构成有:初始值,控制参数及序列的长度n。当l=256时,该算法产生的序列如图4所示,从图中可以看出序列值具有均匀分布性。
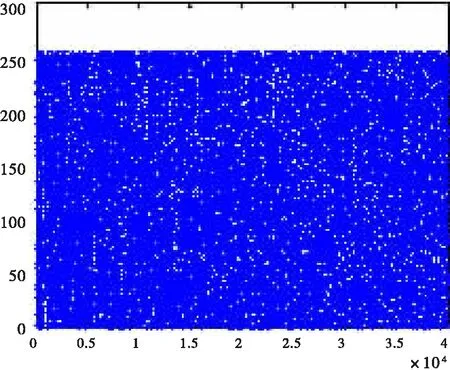
图4 伪随机序列值的分布图
3 混沌伪随机序列的分析
3.1密钥空间分析
伪随机序列发生器的一个重要用途就是用来产生加密密钥,为了保证加密的安全性[15],其密钥空间应不小于2128。本文以细胞神经网络混沌系统的初始值和控制参数作为密钥,密钥空间的大小取决于混沌系统的初值和控制参数的敏感性。经过实验证明,该算法精确到小数点后11位,密钥空间为1011*8=1088≈2290,远大于2128的密钥空间,足以抵抗穷举密钥攻击[16]。
3.2初值敏感性分析
为了保证系统的安全性,一个好的加密系统必须对密钥有敏感性[8]。对本文提出的算法的密钥的敏感性进行了测试,通过轻微改变密钥的初始值,来观察产生的序列与原始序列是否变化,从而达到测试的目的。利用本文提出的伪随机算法产生两组序列,其中一组为原始序列S1,另一组序列为S2,S2是在细微改变任意一个初始值(相差10-11),迭代10 000次后产生的序列,从图5可以看出S1和S2是两个不同的序列,说明该算法对密钥初始值具有敏感性。

图5 S1与S2的差异图
3.3相关性分析
相关性是混沌序列重要的性质,良好的相关性是系统能够可靠运行的保证之一。相关性包括自相关和互相关,对于理想的随机序列,自相关函数应为δ函数,互相关函数应为0。当系统参数b=2、c=12、d=13、e=99,系统初值x(0)=1、y(0)=2、z(0)=3、w(0)=4时,系统迭代10 000次后,产生如图6与图7所示的二进制序列的自相关和互相关特性。从图6和图7可以看出,二进制序列具有类似δ-like的性质,有尖锐的自相关特性和良好的互相关特性。
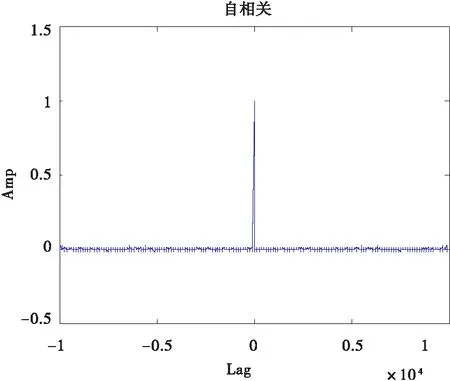
图6 序列的自相关特性
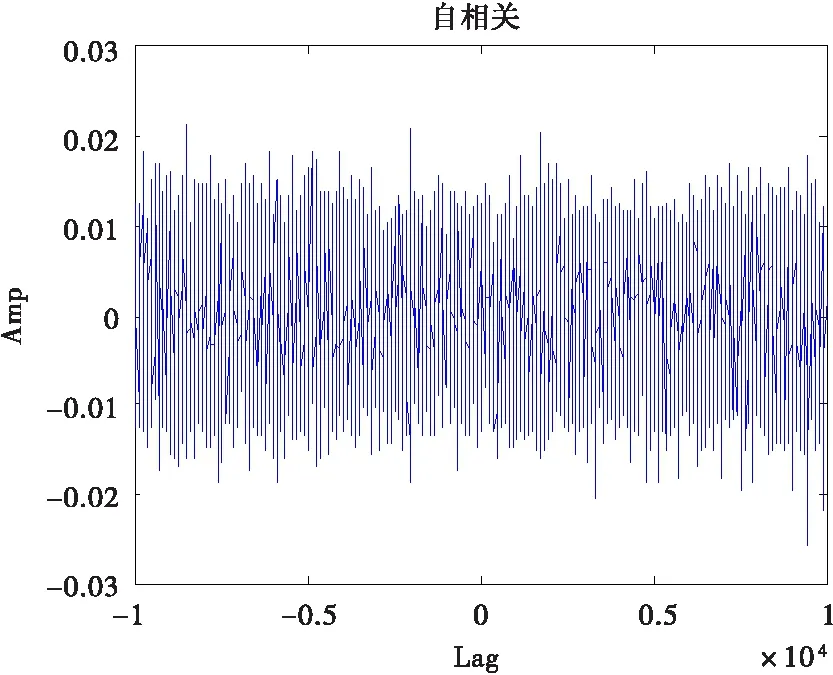
图7 序列的互相关特性
3.4随机性测试
本文采用NIST标准中部分测试方法对文中所产生的二进制序列进行测试,该测试标准为美国国家标准技术研究所制定的随机序列测试标准,即SP800-22标准。该标准从不同角度检验伪随机序列在统计特性上相对于理想随机序列的偏离程度,一般认为通过了该检验标准的伪随机序列具有好的随机性能[5]。
3.4.1 频率测试
频率测试的目的是检验整个序列中0和1的比例,即测试序列中0和1的比例是否近似相等,约为50%。具体的测试方法如下[17]:
(1) 将由0和1组成的序列转换为由-1,1组成的序列,转换方式为xi=2ε-1。其中,ε、xi为转换前后的比特值。计算转换后的序列的和Sn,即Sn=x1+x2+x3+…+xn。
(2) 计算统计值sobs,即
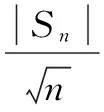
(5)
(3) 计算判断标准P-Value的值:

(6)
其中,erfc()为互补误差函数,即
(7)
若P-Value的值小于0.01,则认为测试的序列不为随机序列;反之,则认为序列是随机序列。
取迭代初值x(0)=1、y(0)=2、z(0)=3、w(0)=4,系统参数b=2、c=12、d=13、e=99,迭代次数N=10 000,生成长度为40 000的二进制序列,通过统计,二进制混沌序列中‘0’的个数N0=19 973,‘1’的个数N1=20 027,0-1之比为N0/N1=0.9973,由上述测试方法得P-Value=0.7872>0.01,故可认为序列是随机序列。
3.4.2 游程测试
游程是指序列中由相同比特所构成的不间断的子序列。游程测试的目的是计算序列中游程的个数,并判断0和1的游程个数是否与随机序列一致。同时,该项测试还可以用于判断序列在0和1之间的振荡快慢[18]。
在这里,只关心序列是否是随机的,不关心序列是否具有某种倾向,故采用双侧假设检验,在假设为真的情况下,0和1出现的可能性相等,其在序列中应是交互的。相对于一定个数的‘0’和‘1’,序列游程的总数应在一定范围内。若游程总数过少,表明某一游程的长度过长,意味着有较多的0或1相连,序列存在成群倾向;若游程总数过多,表明某一游程的长度过短,意味着‘0’和‘1’频繁交替,序列具有混合倾向。因此无论游程总数过多或过少,都表明序列不是随机的。
同样,取迭代初值x(0)=1、y(0)=2、z(0)=3、w(0)=4,系统参数b=2、c=12、d=13、e=99,迭代次数N=10 000,生成长度为40 000的二进制序列,利用双侧假设检验测试游程,得到游程数为20 014,在显著性水平0.05下的检验结果为0.1438,小于显著水平0.05下的正态上0.025分位点的值1.9600,接受独立假设。故可认为序列是随机序列。
4 结束语
本文基于超混沌细胞神经网络系统设计了一种伪随机序列生成算法,该算法能同时生成两种伪随机序列。通过理论分析和仿真验证可知,该序列生成器能够产生均匀分布的序列,并且具有良好的自相关和互相关特性。除此之外,本文还利用NIST标准中部分指标对序列发生器进行性能检验,检验结果表明该序列发生器能够产生良好的伪随机序列,该发生器产生的伪随机序列可以作为密码系统的密钥,具有较高的安全性和保密性,具有较好的应用前景。
[1] 马英杰,于航如.Tent混沌伪随机序列发生器设计与实现[J].北京电子科技学院学报,2015,23(4):61-64.
[2] 孙克辉,叶正伟,贺少波.混沌伪随机序列发生器的FPGA设计与实现[J].计算机应用与软件,2014,31(12):7-11.
[3] LEE W B,CHEN T H.A public verifiable copy protection technique for still images[J].Journal of Systems & Software,2002,62(3):195-204.
[4] GARCIA-MARTINAZ M,CAMPOS-CANTON E. Pseudo-random bit generator based on lag time series[J].Int J Mod Phys C,2014,25(4):822-836.
[5] WANG X Y,QIN X,XIE Y X.Pseudo-random sequences generated by a class of one-dimensional smooth map[J].Chinese Physics Letters,2011,28(28):080501.
[6] HAMZA R.A novel pseudo random sequence generator for image-cryptographic applications[J].Journal of Information Security and Applications,2017,35(1):119-127.
[7] FRANOIS M,GROSGES T,BARCHIESI D,et al.Pseudo-random number generator based on mixing of three chaotic maps[J].Communications in Nonlinear Science & Numerical Simulation,2014,19(4):887-895.
[8] HU H P,LIU L F,DING N D.Pseudo-random sequence generator based on the Chen chaotic system[J].Computer Physics Communications,2013,184(3):765-768.
[9] WANG X,LUAN D,BAO X.Cryptanalysis of an image encryption algorithm using Chebyshev generator[J].Digital Signal Processing,2014,25(1):244-247.
[10] WANG Q,YU S,LI C,et al.Theoretical design and FPGA-based implementation of higher-dimensional digital chaotic systems[J].IEEE Transactions on Circuits & Systems I Regular Papers,2015,63(3):401-412.
[11] 冯汉,索宇,朱培勇.基于Logistic映射的迭代式的混沌特性及混沌控制[J].四川理工学院学报:自然科学版,2011,24(1):24-26.
[12] 朱艳平.初始值对细胞神经网络混沌特性的影响[J].赤峰学院学报:自然科学版,2016,32(1):38-40.
[13] 张严平,陆锐敏.一种改进的混沌序列量化算法[J].通信技术,2016,49(3):278-281.
[14] 唐立法,周健勇,董斌辉,等.混沌量化算法研究及测试分析[J].微型机与应用,2010,29(19):13-24.
[15] AKHSHANI A,AKHAVAN A,MOBARAKI A,et al.Pseudo random number generator based on quantum chaotic map[J].Communications in Nonlinear Science and Numerical Simulation,2014,19(1):101-111.
[16] 齐迎宾,孙克辉,王会海,等.超混沌伪随机序列生成器设计与性能分析[J].计算机工程与应用,2017,53(4):135-139.
[17] 李红燕,杨万利.时空混沌二值化方法研究[J].计算机工程与应用,2013,49(21):65-69.
[18] 刘金.无线传感器网络密钥管理与信息加密研究[D].沈阳:东北大学,2014.
DesignofPseudo-RandomSequenceGeneratorBasedonCNNHyperchaoticSystem
ZHANGQin,LINDa,XULi
(School of Automation & Information Engineering, Sichuan University of Science & Engineering, Zigong 643000, China)
A design of pseudo random sequence generator is proposed based on CNN hyperchaotic system. Theory analysis and simulation show that the cellular neural network is good with complex dynamic characteristics, such as great sensitivity to initial values, large key space, which is quite adequate to be the pseudo random sequence generator. This generator based on hyperchaotic system can generate two different sequences, one is the binary and the other is decimal, and the sequence is good with performence such as uniform distribution, sharp autocorrelation characteristics and good cross-correlation. Furthermore, the generated pseudo random sequence passed NIST test successfully. It is good in practical applications.
hyperchaotic; cellular neural network; pseudo random sequence generator
TN918
A
2017-07-29
国家自然科学基金项目(61640223);人工智能四川省重点实验室开放基金(2016RZJ02)
张 琴(1989-),女,江苏扬州人,硕士生,主要从事混沌保密通信与图像加密方面的研究,(E-mail)820441750@qq.com;
林 达(1974-),男,山东日照人,教授,博士,硕士生导师,主要从事混沌保密通信、非线性系统的智能控制与化与无人机运动协调控制方面的研究,(E-mail)971244320@qq.com
1673-1549(2017)05-0057-06
10.11863/j.suse.2017.05.10

