出租车管理三方博弈与管理策略仿真*
宋成举 张亚平 吴 彪
(黑龙江工程学院汽车与交通工程学院1) 哈尔滨 150050)(哈尔滨工业大学交通科学与工程学院2) 哈尔滨 150090)
出租车管理三方博弈与管理策略仿真*
宋成举1)张亚平2)吴 彪1)
(黑龙江工程学院汽车与交通工程学院1)哈尔滨 150050)(哈尔滨工业大学交通科学与工程学院2)哈尔滨 150090)
出租车管理由于存在多个主体,主体之间的复杂关系使得出租车管理问题及内部运行机制尚不明确.综合考虑出租车、出租车公司和管理部门之间的博弈关系,给出博弈参与者策略集,分析不同策略组合下各参与者的收益函数,建立不同策略组合条件下的收益矩阵,采用复制动态方程描述博弈参与者策略变化,应用系统动力学软件构建管理策略仿真环境,仿真分析不同策略条件下博弈参与者策略变化曲线.结果表明,纯策略、混合策略及各种经济学策略条件下,系统均能达到稳定态,但波动过程呈现开放性.因此,单一策略无法令系统收敛.
出租车管理;博弈;系统动力学;管理策略;稳定态
0 引 言
出租车作为城市惟一的个性化公共交通方式,以其特有的灵活性、机动性、时间性,获得居民出行的广泛青睐.随着居民出行要求的不断提高和出行需求的持续增长,出租车管理中存在的问题日益凸显,特别是在冬季的北方城市更为突出.出租车违规运营、出租车公司监管不到位、管理部门执法能力不足等问题都暴露出来,这使得出租车管理问题逐渐成为一个突出的交通问题.目前,我国出租车以“公司制”模式运营,即出租车接受出租车公司的日常管理,同时,出租车公司和出租车接受政府部门的监管.而作为商业化色彩浓重的出租车个体和出租车公司均具有逐利的本能,其从事出租运营服务行为的最终目的是实现利益的最大化,但受制于管理部门的监管,其具体行为仍受到管理约束.
围绕出租车管理问题国内外学者开展了较多的理论研究与实践,Viegas[1]分析了出租车在城市出行服务方面的机遇和挑战,应用博弈理论剖析出租车新技术与监管水平之间的博弈关系,促进二者的协同联系,进而提高出租车服务效率;Rosa等[2]应用遗传算法解决了出租车在机场的管理问题,通过仿真模拟,应用圣保罗机场的数据证明了该方法的有效性;Bai等[3]应用博弈理论解决了出租车调度问题,通过计算纳什均衡实现乘客和出租车之间的合作共赢; Li等[4]应用非合作博弈理论分析车道路选择问题,并找出了纳什均衡,采用SUMO,MOVE和TraCI的模拟方法验证模型有效性;孙启鹏等[5]运用博弈理论解析出租车公司与司机的动态博弈过程,明确各博弈路径的收益函数和各主体的博弈均衡条件,通过求解最优子博弈纳什均衡,给出管理费合理范围的测算方法;袁长伟等[6]构建了神经元S特性函数形式的出租车拒载函数,引入出租车市场规模、等候时间、价格等市场参数,讨论存在拒载行为的出租车市场供需平衡机制,并构建考虑拒载的以社会福利最大化为目标的出租车市场优化模型;庄立坚等[7]依托大规模浮动车数据的分析和预处理,提出面向出租车运营管理的大规模浮动车数据处理框架,构建基于浮动车数据的出租车运营管理指标体系及其计算模型.
当前的研究主要集中在出租车调度优化、路径优化等方面,在出租车监管博弈分析与仿真方面有待深入开展研究.本文应用博弈论分析出租车管理中的博弈关系,采用系统动力学理论仿真分析出租车管理策略的实施效果.
1 出租车监管博弈关系分析
在出租车运营与管理中,存在出租车、出租车公司和管理部门三个参与主体,在该三方博弈过程中,出租车作为交通服务的提供方,负责出租车的实际运营;管理部门作为出租车和出租车公司共同的管理方,负责对所辖的出租车和出租车公司实施监督与管理;出租车公司作为出租车的管理方和管理部门的被管理方,负责出租车的管理,并接受管理部门的监督.
假定博弈行为的三个参与主体均为有限理性的.假定管理部门以概率α(0≤α≤1)对出租车的运营状况进行检查,α值越高表示管理部门的检查力度越强,出租车被检查的频率越高,反之则检查能力越差.假定管理部门能够严格执法,在执法过程中不存在权力寻租的情况,管理部门的检查活动需要支付一定的成本,该成本包括:平均每次检查的成本C1,如果出租车违规运营,管理部门将承受相关的期望损失C2;如果管理部门通过检查发现出租车的违规运营问题,将对该出租车处以相应的罚款,罚款收益为C3,发现出租车公司存在不严格管理,对所在的出租车公司进行罚款,罚款收益为C4,检查未发现违规运营和不严格管理行为时,则对出租车及所在出租车公司进行一定的奖励,出租车的奖励收益为C5,出租车公司的奖励收益为C6.
出租车则以概率β(0≤β≤1)采取拒载、套牌车等违规运营策略,β值为出租车的违规行为的严重程度.假定出租车按管理规定运营时,其所获得的正常收益为B1,而当采取违规策略时,其所获得的额外收益为B2.
出租车公司以概率γ(0≤γ≤1)对出租车的日常运营进行监督与管理,γ值为出租车公司的管理强度,γ值越大表示出租车公司的管理越严格,出租车公司按照管理规定所获得的正常收益为P1,但当管理强度下降时,出租车公司将承担一定的机会成本P2,不严格管理时,出租车公司可节约管理成本P3,出租车公司通过严格管理,发现出租车存在违规行为,对出租车的惩罚收益为P4,当发现出租车不存在违规行为,对出租车的奖励为P5.
根据上述分析,该博弈过程的参与人集合可表示为:i∈Ω,i={1,2,3}.其中:i=1代表管理部门;i=2代表出租车;i=3代表出租车公司.
每个博弈的参与者所对应的策略空间可表示为:Si,i={1,2,3};其中管理部门的策略空间为S1= {S11,S12}={检查,不检查},出租车的策略空间为S2= {S21,S22}={违规运营,遵规运营};出租车公司的策略空间为S3= {S31,S32}= {严格管理,不严格管理},每个参与者所对应的收益函数记为ui,i={1,2,3}.
当管理部门采取检查策略,出租车采取违规运营,出租车公司采取严格管理时,管理部门收益函数可以表示为
u1{S11,S21,S31}=-C1+C3-C6
(1)
而对于出租车而言,其收益函数可以表示为
u2{S11,S21,S31}=B1+B2-C3-P4
(2)
对于出租车公司而言,其收益函数可以表示为
u3{S11,S21,S31}=P1+C6+P4
(3)
同理,根据上述假设,给出管理部门、出租车和出租车公司三者之间的收益矩阵见表1.

表1 三方博弈收益矩阵
2 三方博弈模型构建
将管理部门选择检查的期望收益记为Uα,选择不检查的期望收益为U1-α;出租车选择遵规运营的期望收益为Uβ,选择违规运营的期望收益为U1-β;出租车公司选择严格管理的期望收益为Uγ,选择不严格管理的期望收益为U1-γ.
根据期望计算公式,将管理部门的收益函数代入后整理可得
Uα=β(C5+C3)-γ(C6+C4)+
(-C1+C4-C5)U1-α=-βC2
(4)
则管理部门的平均期望收益可表示为
U1=αUα+(1-α)U1-α
(5)
将公式代入后整理得
U1=αβ(C5+C3+C2)-αγ(C6+C4) +
α(-C1+C4-C5)-βC2
(6)
在演化博弈中指出:在博弈过程中,某一参与者所采取的策略概率的变化率与两个因素有关:一个是上一时刻的策略比例,另一个是纯策略收益与平均期望收益之间的差值.用公式可以表达为
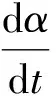
α(1-α)(β(C5+C3+C2)-
γ(C6+C4)+(-C1+C4-C5))
(7)
式(7)为管理部门的策略概率变化率.同理,出租车及出租车公司的策略概率变化率可表示为
Uβ=B1+B2-αC3-γP4
(8)
U1-β=B1+αC5+γP5
(9)
U2=B1+γP5+αC5+βB2-
αβC3-βγP4-βγP5-αβC5
(10)
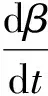
β(1-β)(B2-αC3-γP4-αC5-γP5)
(11)
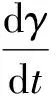
γ(1-γ)(α(C6+P2+C4)+
β(P4+P5)-P3-P5)
(12)
(13)
式中:X1~X8为鞍点;X9~X15为中心点.所以,该三方博弈中不存在稳定的演化均衡.
3 仿真环境构建
针对出租车管理问题,应用系统动力学仿真软件Vensim PLE构建涵盖管理部门、出租车公司和出租车三者的演化博弈模型,模型中分为三个模块,包括三个水准变量、三个速率变量、13个外部变量、30个中间变量.
假设INITIAL TIME=0,FINAL TIME=1 000,TIME STEP=0.5.模型中涉及到的主要方程如下:
检查=INTEG(检查变化率)
违规=INTEG(违规变化率)
严格=INTEG(严格变化率)将变量值带入表1,应用划线法选择纯策略下的纳什均衡,计算结果见表2.由表2可知,没有一个纯策略能够保证所有参与者收益均有短线,即该博弈问题不存在纯策略纳什均衡.

表2 三方博弈收益矩阵计算值
3.1 纯策略仿真
假定在博弈过程中,每个博弈参与者的策略初始值均为纯策略,而各博弈参与者由于均具有0,1两种选择,因此,其对应的策略组合为23=8个,根据模型求解的特性可知,此时所形成的策略组合分别对应于X1~X8中的一项,通过上述的方程求解可以看出:在三方博弈过程中,当初始策略均为纯策略时,所有参与者的策略变化方程取值为0,即没有任何一方改变自身的纯策略.但在实际中,上述组合却并往往不是最优的,以X1=(0 0 0)T为例,在模型中,该组合表示:管理部门不检查,出租车不违规,出租车公司不管理.在该条件下所形成的稳定可以看作是在整个博弈关系群体中没有任何个体采取新策略,以出租车群体为例,表示在出租车群体中不存在任何个体改变自身策略的情况,因此,该博弈显然属于一种典型均衡的状态,但可以预见,该均衡状态是极其不稳定的,一旦在出租车或其他博弈参与者群体中某一参与者通过改变自身策略而获取更大的收益时,该均衡态必将迅速打破.
为了证明该分析结论,仍以X1=(0 0 0)T为例,当管理部门与出租车公司的初始策略概率不变,而出租车开始仅以0.01的微小初值进行违规时,其三方博弈的演化过程见图1.
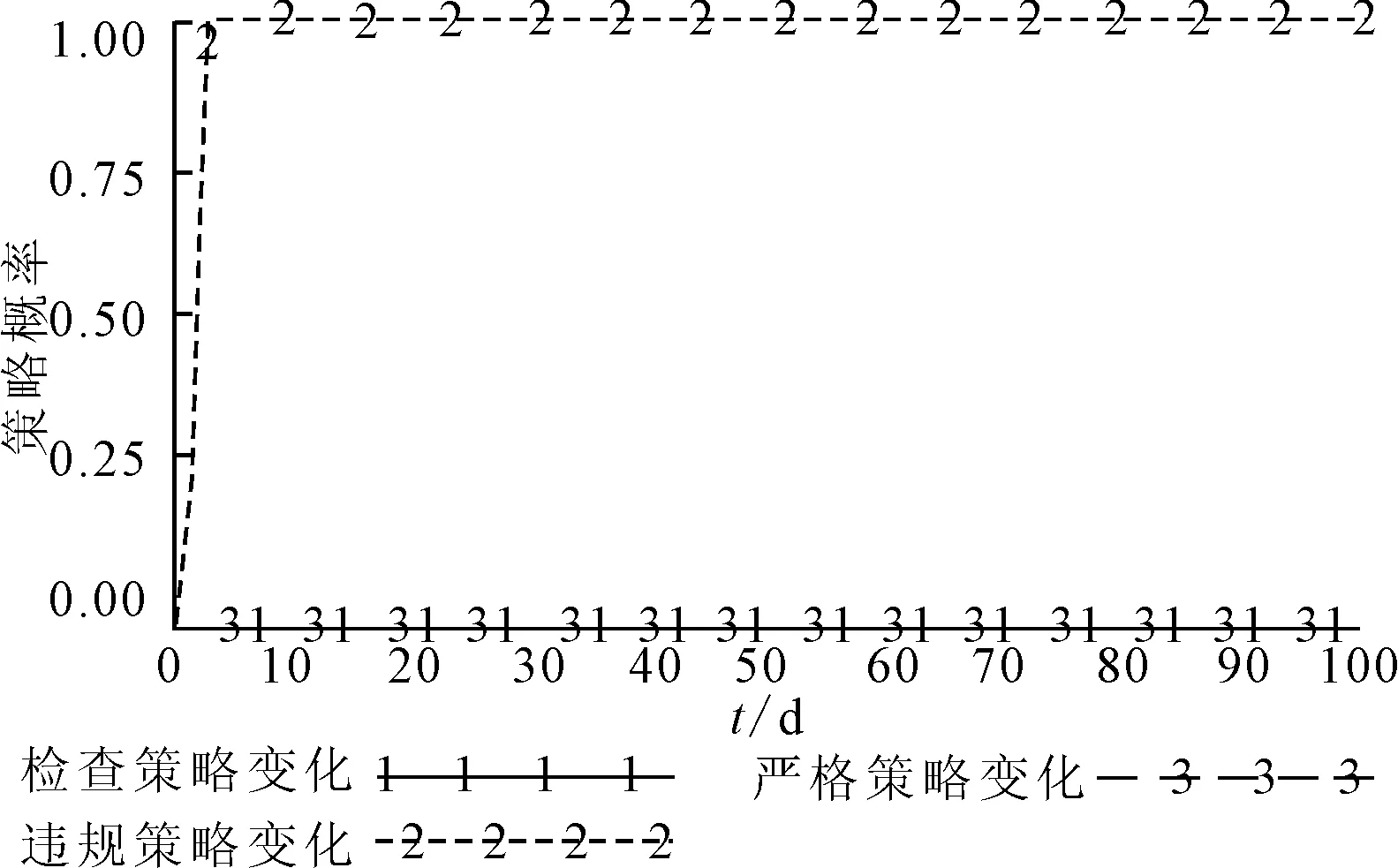
图1 出租车策略突变条件下三方策略演化
由图1可知,尽管出租车初始策略变化很小,仅为0.01,但由于这种变化会使得出租车个体获取较高的收益.因此,迅速成为出租车群体模仿和学习的对象,使得采取新策略成为群体的共识,因此,最终的系统稳定状态由X1=(0 0 0)T演化为X3=(0 1 0)T.
3.2 混合策略仿真
当博弈参与者的初始策略为复制动态方程中的临界点X9~X15时,即三方的初始策略为混合策略时,其博弈演化情况与初始策略为纯策略的情况类似,三方受益均未随着时间变化而产生波动,因此,其演化结果为均衡状态,为了进一步分析出租车管理中三方博弈的均衡问题,利用前文所建立的动态博弈模型,通过仿真可以得到管理部门、出租车和出租车公司以初始策略(0.2,0.4,0.7)条件下的策略变化曲线,见图2.
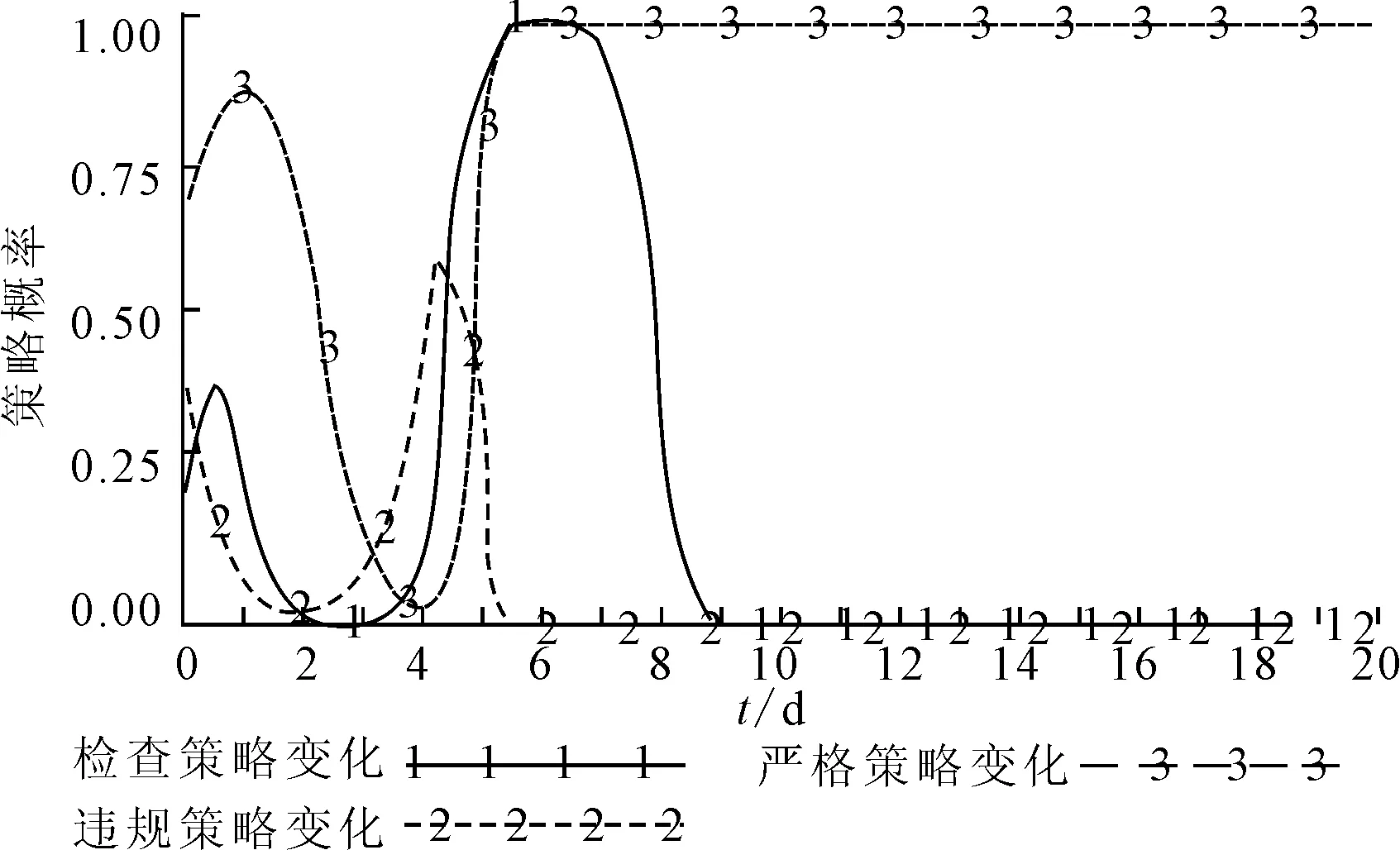
图2 博弈三方策略变化曲线
图2中的曲线分别表示管理部门、出租车和出租车企业选择检查、违规和严格策略的概率变化,从仿真结果中可以看出,在当前初始条件下,管理部门检查策略、出租车违规策略和出租车公司的严格管理策略的变化均呈现波动放大的趋势,波动幅度逐渐增大,波动频率也逐渐增大,直至达到稳定状态.
4 管理策略仿真分析
4.1 加大惩罚力度
在原有模型仿真环境下,假设第10 d开始加大对出租车违规以及出租车公司不严格管理的惩罚力度,即将对出租车违规运营的罚款收益值由5变为8,同时对出租车公司的不严格管理的罚款收益值由2变为5,通过仿真得到博弈参与者策略变化曲线见图3.
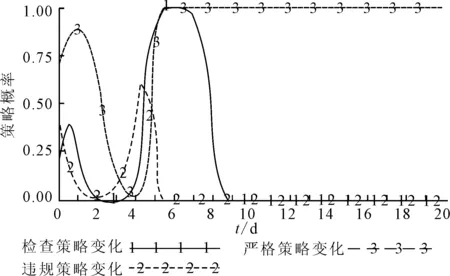
图3 加大惩罚力度条件下三方策略演变曲线
图3中曲线分别代表管理部门、出租车和出租车公司选择检查策略、违规策略和严格管理策略的概率变化曲线,从仿真结果中可以看出,当在第10 d提高对出租车违规行为的惩罚力度后,出租车的违规运营概率均值并没有增加,而是呈现了一定程度的下降;但对于管理部门和出租车公司来说,惩罚力度的加大对各自策略的选择几乎没有影响.
4.2 改变检查成本
在原有仿真环境下,假设检查成本由0.5变为2,通过仿真得到管理部门和出租车违规运营的策略变化曲线见图4.
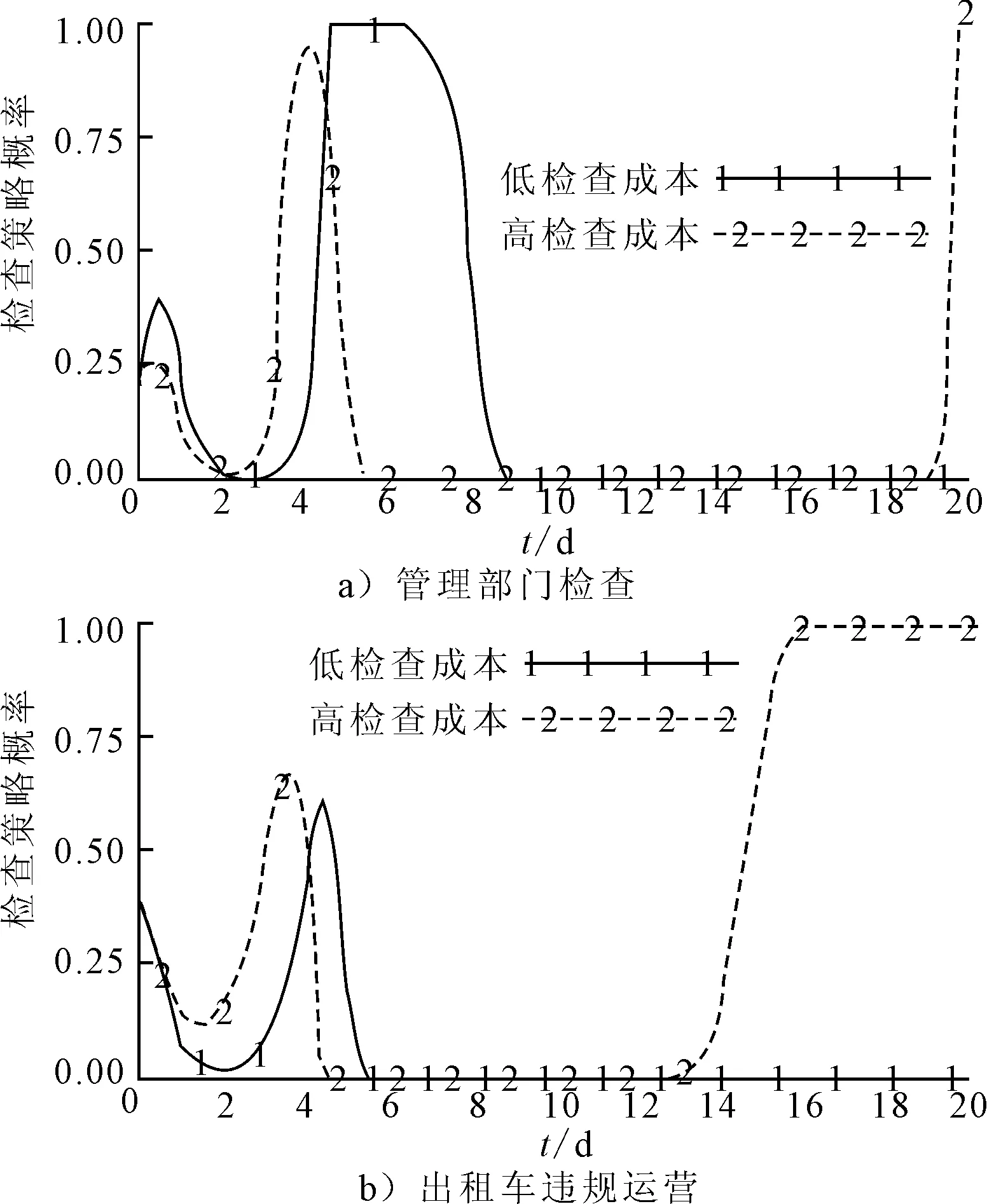
图4 不同检查成本条件下策略变化曲线
图4a)中的两条曲线分别表示管理部门在低检查成本和高检查成本条件下采取检查策略的概率变化曲线.从仿真结果中可以看出,随着管理成本的增加,管理部门的检查概率的幅值明显降低,且波动频率明显增加,说明高检查成本制约了管理部门检查的积极性,使得管理策略的波动频率呈现上升趋势.图4b)中的两条曲线分别表示出租车在低检查成本和高检查成本条件下采取违规运营策略的概率变化曲线.从仿真结果中可以看出,随着检查成本的增加,出租车违规运营呈现一定的上升趋势,且波动频率明显上升,这主要与管理部门的检查强度有关,由于管理部门受制于检查成本而降低检查强度,出租车在违规收益的吸引下,更倾向于选择违规运营策略.
4.3 提高奖励额度
将对出租车遵规运营的奖励额度由0.5变为2,对出租车公司严格管理的奖励额度由3变为5,通过仿真得到管理部门检查和出租车违规运营的策略变化曲线见图5.
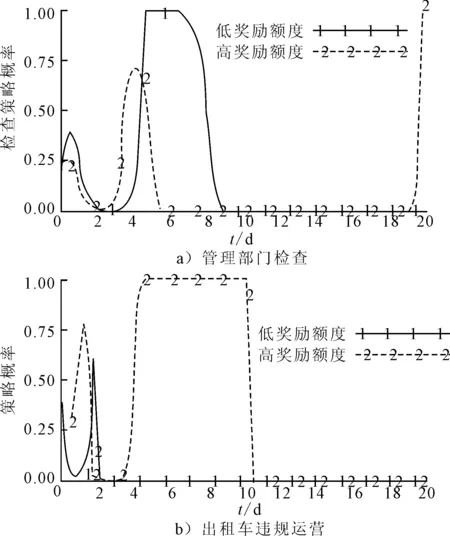
图5 不同奖励额度条件下策略变化曲线
由图5a)可知,高奖励额度使得管理部门选择检查策略的概率明显降低,但该博弈的波动频率增大.由图5b)可知,高奖励额度不但没有使出租车的违规运营概率降低,反而有了一定程度的增加,波动进一步加剧.
5 结 论
1) 出租车管理过程中存在多个参与主体,主体之间存在明显的博弈关系.
2) 纯策略条件下,系统能够保持稳定,且系统具有自学习功能,在收到微小扰动的情况下,系统可以通过学习而迅速恢复到稳态.
3) 混合策略条件下,系统波动呈现放大趋势,直至稳定态.
4) 惩罚力度、检查成本和奖励额度的变化对于提高博弈参与者策略稳定性效果不明显.
[1] VIEGAS J M. Taxis: bridging the gap between individual and collective transport[J]. Public Transport International,2008,57(2):118-125.
[2] ROSA L P, FERREIRA D M, CRUCIOL L L B V, et al. Genetic algorithms for management of taxi scheduling[C]. Proceedings on the International Conference on Artificial Intelligence (ICAI),The Steering Committee of The World Congress in Computer Science, Computer Engineering and Applied Computing, Las Vegas,2013.
[3] BAI R, LI J, ATKIN J A D, et al. A novel approach to independent taxi scheduling problem based on stable matching[J]. Journal of the Operational Research Society,2014,65(10):1501-1510.
[4] LI J P, HORNG G J, CHEN Y J, et al. Using non-cooperative game theory for taxi-sharing recommendation systems[J]. Wireless Personal Communications,2016,88(4):761-786.
[5] 孙启鹏,张兆芬,邹海波,等.利益博弈下的城市出租车管理费测算[J].交通运输系统工程与信息,2014,14(5):87-92.
[6] 袁长伟,吴群琪,韦达利,等.考虑拒载的出租车市场平衡机制与优化模型[J].中国公路学报,2014,27(6):91-97.
[7] 庄立坚,韦清波,何兆成,等.基于浮动车数据的出租车运营管理特性建模与分析[J].重庆交通大学学报(自然科学版),2014,33(4):122-127.
Tripartite Game on Taxi Management and Strategy Simulation
SONGChengju1)ZHANGYaping2)WUBiao1)
(SchoolofAutomotiveandTransportationEngineering,HeilongjiangInstituteofTechnology,Harbin150050,China)1)(SchoolofTransportationScienceandEngineering,HarbinInstituteofTechnology,Harbin150090,China)2)
Because of the multiple subjects in taxi management, the complicated relationship between different subjects makes the taxi management and the inner mechanism not clear. Considering the game relationship among taxi, taxi company and management department, this paper presents the participants’ strategy set. The income function of each participant is analyzed lin different strategies, and the income matrix under different strategies combination is established. By adopting the duplicated dynamic equation to describe the strategy change and appling system dynamic software on establishing the management strategy simulation environment, the strategy change curves are simulated and analyzed in different strategy conditions. The results show that the system can achieve steady state under pure strategy, mixed strategy and various economic strategies, but the fluctuation process is open. Therefore, a single strategy can not make the system convergent.
taxi management; tripartite game; system dynamics; management strategy; steady state
U116.1
10.3963/j.issn.2095-3844.2017.05.005
2017-08-06
宋成举(1983—):男,博士,讲师,主要研究领域为交通管理策略仿真、交通结构优化
*黑龙江省青年科学基金项目资助(QC2014C060)

