考虑焊接残余应力的构造细节疲劳性能评估*

刘沐宇 罗洪界 邓晓光

(武汉理工大学道路桥梁与结构工程湖北省重点实验室 武汉 430070)

考虑焊接残余应力的构造细节疲劳性能评估*

刘沐宇 罗洪界 邓晓光

(武汉理工大学道路桥梁与结构工程湖北省重点实验室 武汉 430070)

焊接钢结构在桥梁中广泛应用，在焊接过程中不可避免的会产生焊接残余应力，使焊接部位易引发疲劳问题，而现行规范中的细节分类不能反映实际焊接残余应力水平.基于Goodman公式及相关经验理论，提出定量考虑焊接残余应力来修正材料S-N曲线，从而确定构造细节S-N曲线的方法，并验证了其可行性.以钢桁梁斜腹杆过焊孔构造细节为分析实例，采用热-结构耦合的分析方法对其焊接残余应力进行了数值模拟分析，并利用热点应力外推法对其应力集中效应进行了有限元计算，根据所提方法，得到了过焊孔构造细节S-N曲线，为准确评估结构疲劳寿命和抗疲劳设计提供指导.

S-N曲线；焊接残余应力；Goodman公式；构造细节；过焊孔

0 引 言

近年来，对焊接残余应力对结构疲劳性能的影响开展了大量研究.Lee等[1]基于断裂力学理论考虑焊接残余应力对应力强度因子的影响，从而影响结构的裂纹扩展速率，使疲劳强度下降；Do等[2]基于连续损伤力学的方法，研究了焊接残余应力对疲劳损伤度增量的影响，并与不考虑焊接残余应力的结果进行对比分析了焊接残余应力对疲劳寿命的影响.研究表明，焊接结构焊缝处存在高值焊接残余应力，对循环应力幅较低的高周疲劳的影响值得关注，为准确评估结构的疲劳寿命应予以充分考虑[3-5].

现行焊接钢结构疲劳寿命分析主要是基于S-N曲线的方法[6].规范中提供的构造细节S-N曲线，只局限于几种典型的结构形式，并没有考虑焊接残余应力的具体值.而对于新型构造细节，获取其疲劳性能主要依靠疲劳试验的方法，但试验周期长，花费大量的人力、物力和财力，且不具有普遍适用性[7].实际桥梁中的焊接结构尺寸、材料性能和焊接工艺等因素与规范和试验存在一定差异，传统的构造细节疲劳性能确定方法，不能有效反映结构的真实焊接残余应力水平，应用于实际钢桥结构的疲劳寿命评估中可能并不可靠.

本文从材料的疲劳性能出发，基于Goodman公式及相关经验理论，提出了一种定量考虑焊接残余应力修正材料S-N曲线，从而确定构造细节S-N曲线的方法.以钢桁梁斜腹杆的过焊孔构造细节为分析实例，展开具体分析，根据所提计算方法，构建该新型构造细节的S-N曲线，为钢桁梁主桁杆件的疲劳寿命评估提供技术支撑.

1 考虑焊接残余应力的构造细节疲劳性能确定方法

1.1 考虑焊接残余应力的材料疲劳强度修正

材料的疲劳性能主要通过标准试件在应力比R=-1条件下的轴向拉压疲劳试验拟合得到的S-N曲线来表示.其具体形式可以由Basquin公式表示为

(1)

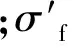
焊接结构的疲劳强度较相应材料的疲劳强度要低很多，主要因为在焊接细节处因焊接施工导致的焊接残余应力，以及几何形状突变引起的应力集中等因素，而使其成为易产生疲劳裂纹的敏感区域，因此，焊接细节热点处实际应力水平为

σtru=σhs+σres=ktσn+σres

(2)

式中:σtru为考虑热点应力和焊接残余应力的实际应力；σres为焊接残余应力，可以采用热-结构耦合的数值模拟方法获得；σhs为热点应力；σn为名义应力；kt为应力集中系数，表示热点应力与名义应力的线性关系，可以通过热点应力外推法及有限元计算分析得到.

故结构中危险点处实际应力幅值为

Δσtru=ktΔσn

(3)

式中:Δσn为名义应力幅值; Δσtru为考虑热点应力和焊接残余应力的实际应力幅值.

焊接残余应力作为一种初始应力，不会改变应力幅的大小，主要通过影响外循环荷载的平均应力来影响结构的疲劳破坏行为.因此，可以通过Goodman线性方法，将实际应力状态等效为平均应力为零的应力状态[8].对于Goodman公式考虑焊接残余应力影响可以表示为

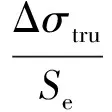
(4)

式中:Δσtru为考虑残余应力的实际应力幅；σmean及σres分别为平均应力和焊接残余应力；Su为材料极限抗拉强度.

对于应力比R=-1的对称循环应力条件下，平均应力为0；同时引入式(3)，以名义应力幅值表示构造细节的疲劳强度，则上式简化为

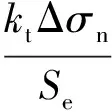
(5)

故可以得到考虑焊接残余应力的材料疲劳强度的修正模型为

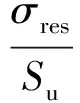
(6)

式中:Se为材料的疲劳强度;SNf为构造细节的疲劳强度.

1.2 考虑焊接残余应力的构造细节S-N曲线确定

文献[9-10]表明,焊接细节的S-N曲线相对于材料斜率更陡，即随着应力幅的增大，焊接细节的疲劳强度相比材料的疲劳强度下降的幅度逐渐减小.因为在高应力幅下，材料会达到屈服状态，其疲劳损伤以延性塑性损伤为主，平均应力的影响减弱，而且焊接残余应力在高应力幅下也会很快松弛，故焊接细节与材料的超低周疲劳强度接近相等，即表现为S-N曲线在低周阶段会相交于一点.因此，有必要考虑焊接残余应力与应力幅的共同作用，对材料S-N曲线的斜率进行相应的修正，以得到焊接细节S-N曲线的斜率.为简化分析，可将低周阶段的这个交点作为焊接结构S-N曲线的第一个拐点B(NB，σB).故假定在此点处，平均应力松弛很快，并且缺口效应很小，甚至可以忽略，即焊接细节的疲劳强度与材料疲劳强度相同，此时的应力幅可按基于大量疲劳试验中得到的经验趋势取为材料极限抗拉强度，即σB=Su，则由式(1)可得

(7)

高周阶段，可取N=2×106对应的点作为平均应力的敏感点，其疲劳强度可以由材料的疲劳强度考虑焊接残余应力等因素的修正获得，则得到焊接结构S-N曲线上的点C(2×106，σC).

由式(1)、(6)求得

(8)

根据Basquin公式形式及其在双对数坐标系下的线性关系，见图1.

图1 构造细节S-N曲线

可以由B，C这两点确定焊接细节S-N曲线斜率及常数：

(9)

据此，通过有限元和经验理论公式相结合的方法，得到了构造细节的S-N曲线模型：

lgN=C-mlgS

(10)

可以定量反映不同焊接残余应力水平对焊接结构疲劳强度的影响.主要计算思路见图2.

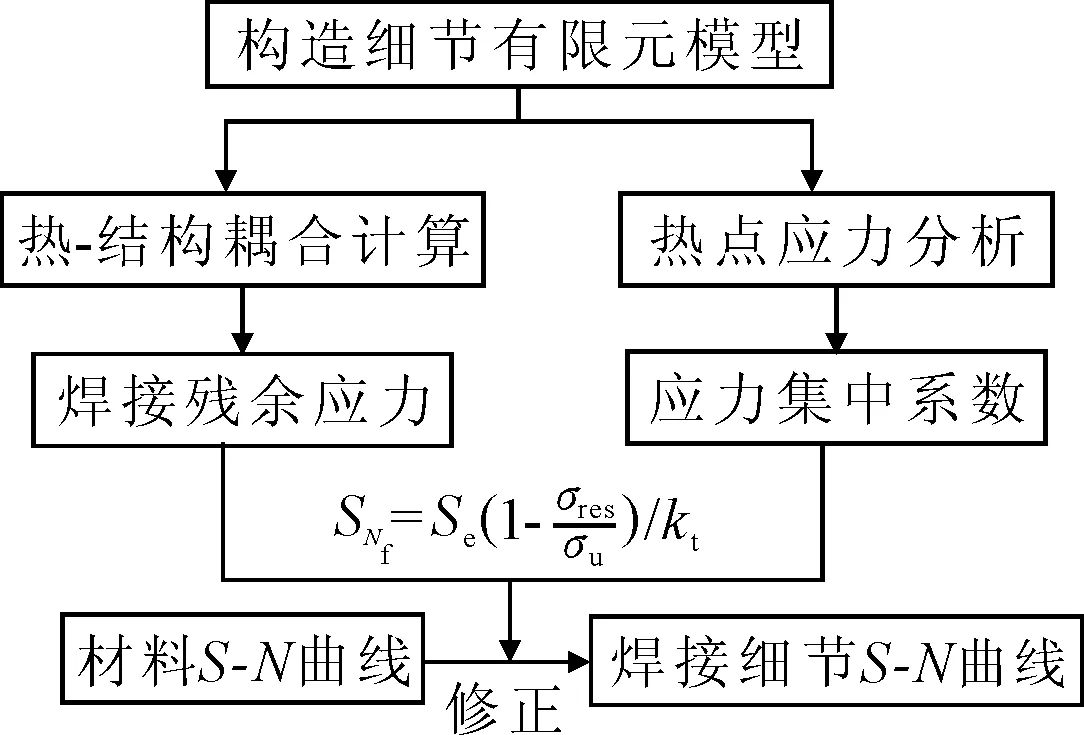
图2 考虑焊接残余应力的构造细节S-N曲线预测方法

1.3 构造细节S-N曲线计算方法验证

为验证本文所提焊接构造细节S-N曲线计算方法的有效性，引用文献[11]中关于正交异性板U肋与顶板焊接细节的疲劳试验资料进行分析验证.根据文献中9个不同荷载水平下的疲劳试验数据结果，拟合得到其试验S-N曲线为

lgN=20.74-6.67 lgσ

该正交异性板U肋采用数值模拟计算和试验实测得到的焊接残余应力值为150 MPa，应力集中系数通过静载试验测得为1.38，材料为Q345B，其材料极限抗拉强度为518 MPa，取钢材Q345的材料S-N曲线为

σ=789.768 8(N)-0.087 1

根据所提构造细节S-N计算模型可以得到其预测的S-N曲线为：lgN=19.52-6.42 lgσ，见图3.

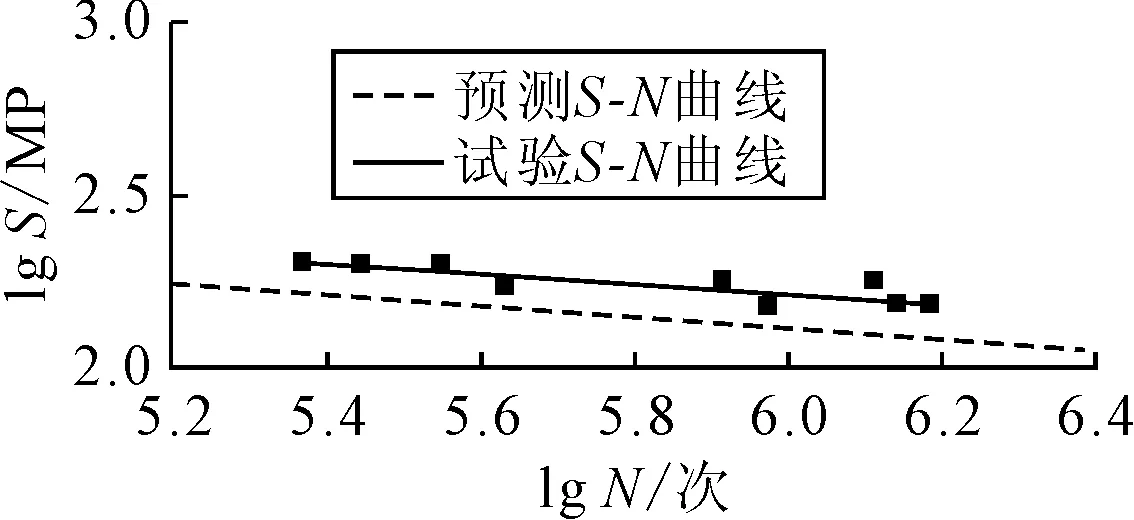
图3 S-N曲线对比验证

由图3可知，针对该构造细节预测的S-N曲线和试验拟合的S-N曲线对比斜率误差为3.7%，常数误差为5.9%，误差较小，能较好地吻合，且疲劳强度稍保守，所有试验数据点都在预测的S-N曲线上方，有足够的安全度，故采用此方法得到构造细节S-N曲线模型，进行钢桥疲劳寿命预测是可行的.

2 主梁新细节实例分析

某大跨径公路钢桁梁悬索桥，荷载水平高，疲劳风险等级大.钢桁梁杆件节段焊接拼装施工时，为避免主桁杆件焊接交叉处引起过大的应力集中，以及焊接施工的方便，在焊缝相交处设有过焊孔，见图4.该过焊孔构造细节因几何形状突变引起应力集中，而且焊缝交错，焊接残余应力分布复杂，是疲劳开裂的薄弱部位.

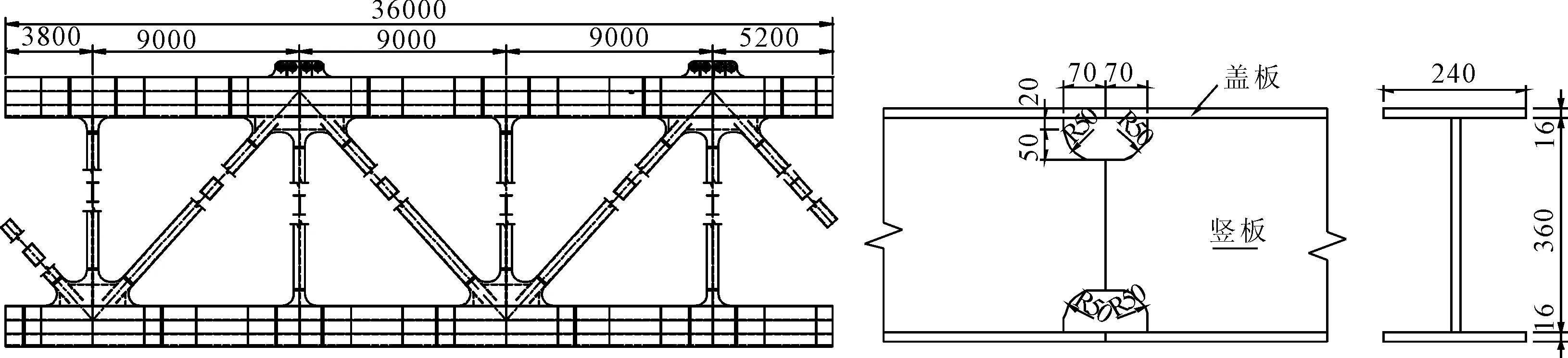
图4 主桁杆件盖板对接焊缝与竖板对接焊缝相交处过焊孔构造(单位：mm)

2.1 焊接残余应力数值模拟

选取贯穿于钢桁梁主桁杆件中焊接交叉部位的过焊孔构造细节为分析对象.基于ANSYS有限元软件，对该过焊孔构造细节建立热-结构耦合有限元模型，为提高计算效率，取其上下对称的一半进行计算分析.为保证计算精度，焊缝附近区域，网格尺寸稍密些，控制在2 mm内.焊缝材料近似按与母材相同的材料处理，材料Q345qD在高温下热物理参数和力学性能参数，见图5.密度和线膨胀系数分别取78 000 kg/m3、1.06×10-5℃-1，按恒值处理.

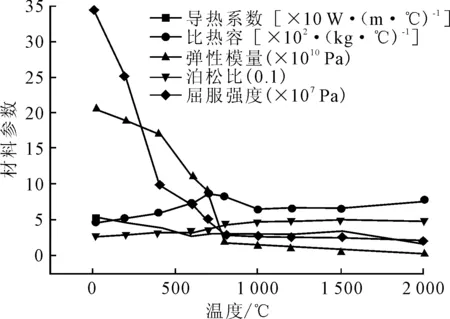
图5 材料热物理及力学性能参数

采用与实桥相同的尺寸和焊接工艺，CO2气体保护焊，焊接参数见表1.考虑到钢桁梁主桁杆件节段焊接施工的实际情况，其焊接顺序见图6：先进行竖板和盖板之间的角焊缝(焊缝①)的焊接和冷却，两条焊缝对称施焊，再对竖板之间以及盖板之间的对接焊缝(焊缝②、③)进行施焊和冷却.

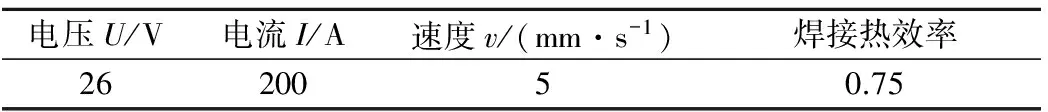
表1 焊接参数

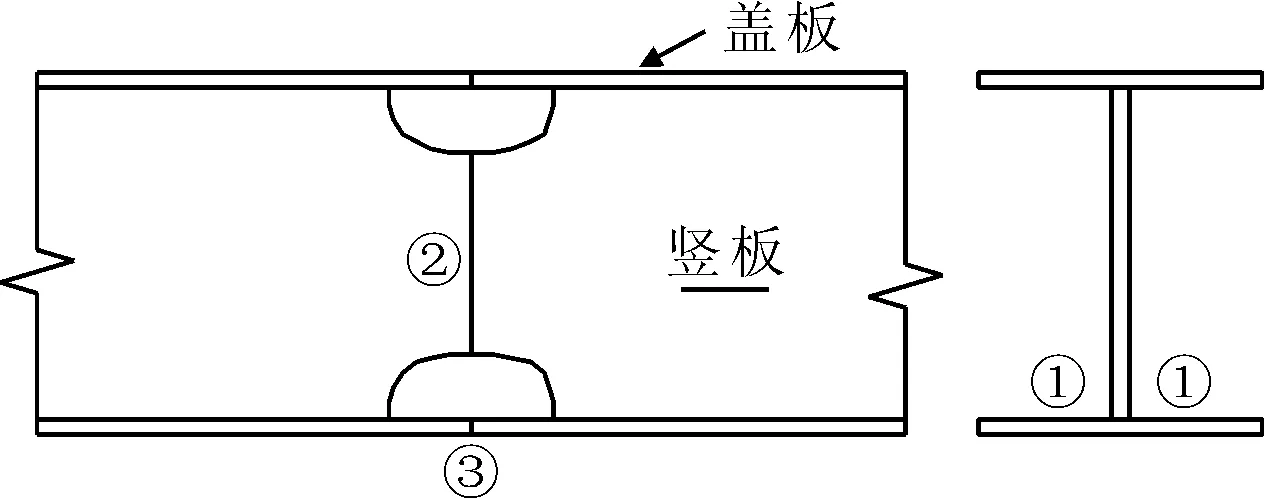
图6 过焊孔构造焊接顺序示意图

2.1.1温度场分析

本文采用的是间接耦合的分析方法.首先进行热分析，选用八节点的六面体实体单元SOL-ID70，初始条件为室温20 ℃，对流边界条件是通过在构件表面设置对流换热系数，以对流荷载来考虑模型与空气之间的热交换.采用生热率为焊接热源，单位时间内生热率为

Q=ηUI/Vh

式中：Q为生热率;η为焊接热效率;U为焊接电压，I为焊接电流;Vh为焊缝单元体积.

通过控制单元的生死和热源的移动来模拟整个焊接过程，得到其温度场分布云图，见图7.

图7 焊接过程中温度场云图(单位:Pa)

由图7可知，每条焊缝在焊接时焊缝区域的温度随着热源的移动，焊缝单元不断被激活，并加热到峰值，最高温度有1 637 ℃，温度影响范围不断扩大，随着冷却时间的推进，温度场分布最终趋于稳定，接近于室温20 ℃，符合实际的焊接过程.

2.1.2应力场分析

由温度场计算结果进行结构分析，将热单元转换为相应的结构分析单元，边界条件取为不使结构发生刚体位移，即在对称面施加对称约束，盖板的左右两侧施加竖向支撑，前后两侧限制其纵向位移.将上步得到的温度场以体荷载形式读入结构模型，进行应力分析，得到最终过焊孔构造细节焊接残余应力分布，见图8～9.

图8 等效焊接残余应力云图(单位:Pa)

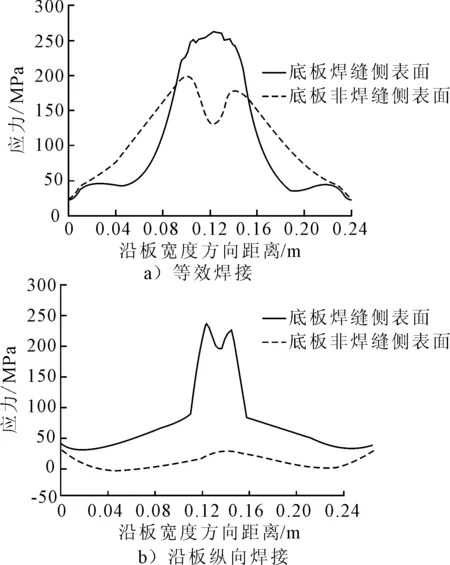
图9 残余应力分布图

由图8可知，焊接残余应力主要集中在焊缝区域，分布比较均匀，等效焊接残余应力最大值为285 MPa，为拉应力，达到了材料屈服强度的82.6%，较大值主要分布于焊趾部位，起焊处最为突出.

过焊孔起弧处焊址部位，是应力集中效应和焊接残余应力影响较为集中的地方，多从此处萌生疲劳裂纹，沿底板宽度方向扩展开裂.分别以该截面位置底板焊缝侧表面及非焊缝侧表面为路径1、2，来研究焊接残余应力的分布，图9为等效焊接残余应力和沿板纵向的焊接残余应力沿路径变化的关系曲线.由图9a)可知，在腹板两侧角焊缝处等效焊接残余应力很大，最大值有262.1 MPa，向外侧远离焊缝方向急剧减小，非焊缝侧底面中心分布有压应力，故等效焊接残余应力有所下降.由图9b)可知，焊缝侧表面在角焊缝中心处焊接残余应力达到最大值255.2 MPa，为拉应力，向两侧远离焊缝方向，焊接残余应力突然减小，最后发展为压应力；非焊缝侧表面以压应力分布为主.

2.2 应力集中系数计算

热点应力为截面危险点处的最大应力，一般通过外推法计算，故可采用有限元的方法来获取其应力集中系数.建立过焊孔构造细节Ansys有限元模型，考虑到网格划分稳定性及精度要求，采用Solid95单元进行计算，网格划分见图10，模型一端固结，另一端施加30 MPa的拉应力均布荷载.顶面施加对称约束.

图10 有限元模型及荷载约束情况

分别采用IIW推荐的线性外推法和二次外推法计算热点应力：

σsh=1.67σ1-0.67σ2

σsh=2.52σ1-2.24σ3+0.72σ4

式中：σ1，σ2，σ3，σ4分别为距热点0.4倍板厚处应力、1倍板厚处应力、0.9倍板厚处应力、1.4倍板厚处应力.计算结果见图11和表2.

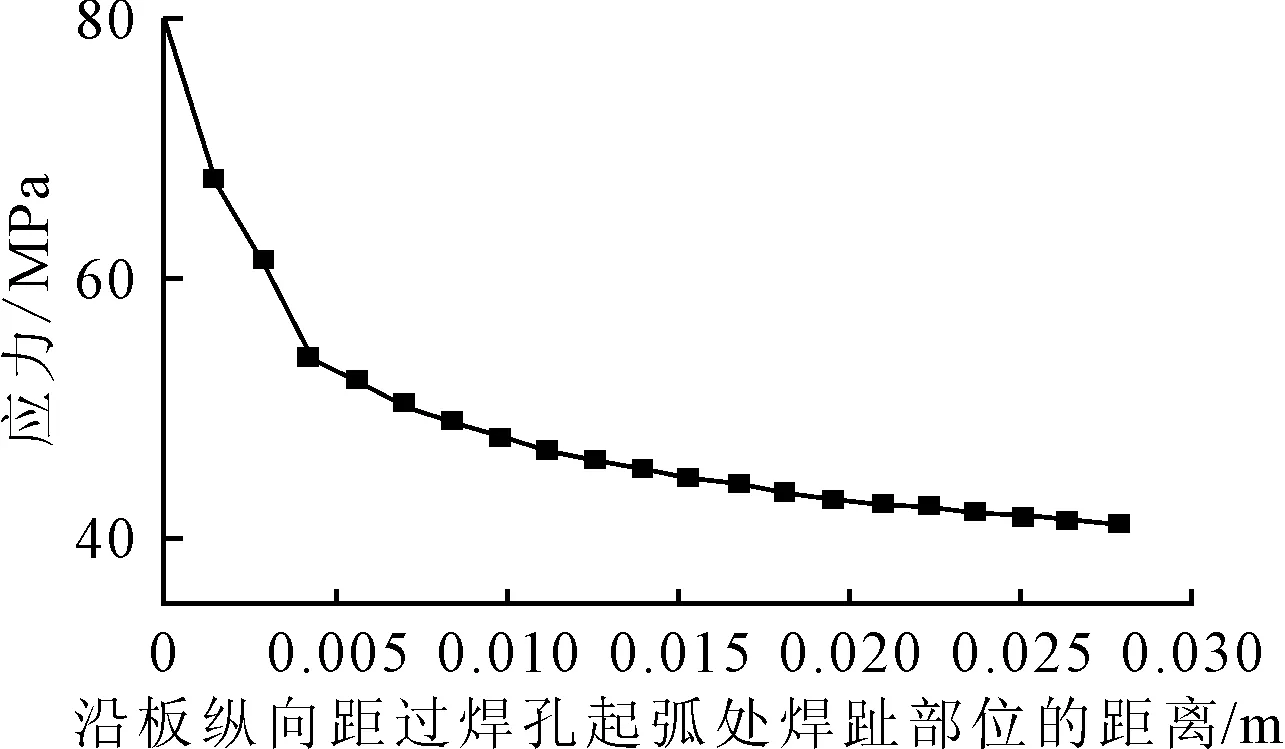
图11 过焊孔应力分布图

表2 应力集中系数计算结果

由表2可见，该过焊孔构造细节在起弧处存在较大的应力集中现象，两种计算方法结果相差不大，从安全角度考虑，取应力集中系数为kt=1.92.

2.3 过焊孔构造细节S-N曲线确定

该过焊孔构造细节材料为Q345qD，其极限抗拉强度为510 MPa，主要承受轴向拉压荷载，钢材Q345qD采用直径10 mm的标准圆棒试件在应力比R=-1的条件下进行的轴向拉压疲劳试验，得到的应力-寿命曲线为

σ=789.768 8N-0.087 1

由此可计算得到S-N曲线第一个拐点NB=152，疲劳强度σB=510 MPa.根据焊接残余应力的数值分析结果，其过焊孔起弧处最大等效焊接残余应力为262.1 MPa，采用所提考虑焊接残余应力的疲劳强度修正模型，并计及应力集中系数(kt=1.92)，可以得到N=2×106对应的疲劳强度σC=56.50 MPa.

根据所提构造细节S-N曲线计算方法可以得到考虑焊接残余应力的过焊孔构造细节的S-N曲线为

lgN=13.85-4.31 lgσ

故通过所提计算方法，可以基于材料的疲劳特性和焊接细节的有限元分析，构建焊接细节的S-N曲线，见图12.有效解决疲劳试验成本费用高、试验周期长、缺乏普遍适用性等问题，为钢桥焊接结构的疲劳寿命评估和抗疲劳设计方面提供很好的指导.

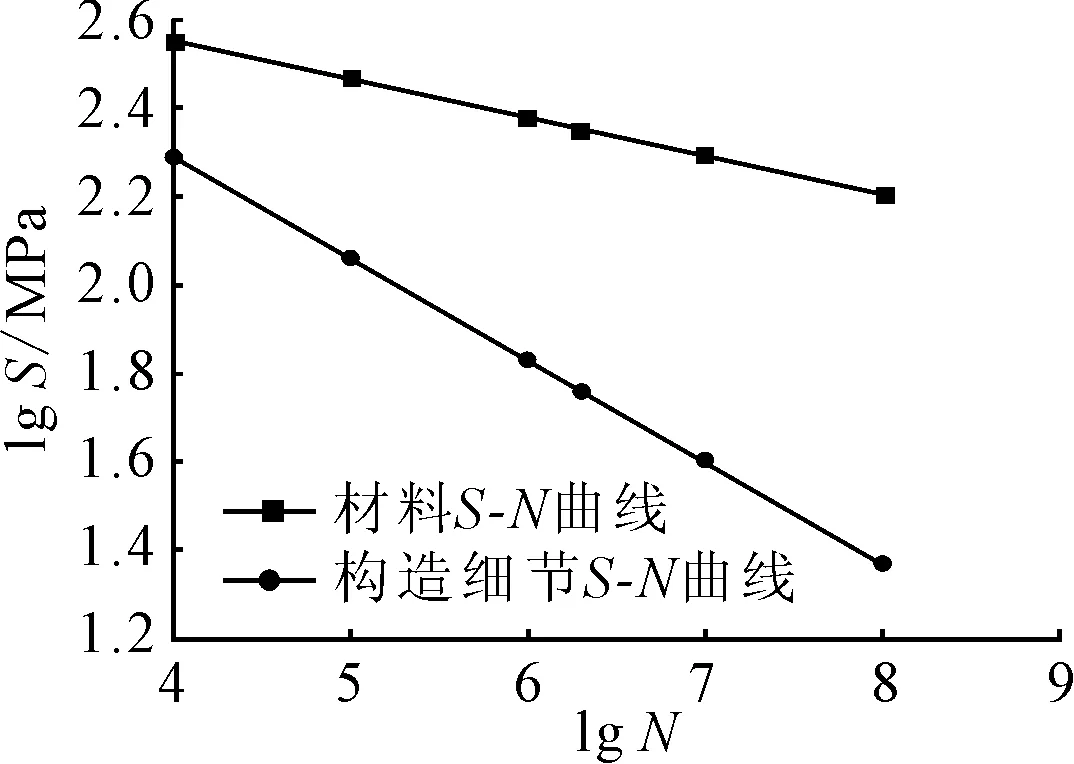
图12 过焊孔构造细节S-N曲线

3 结 论

1) 通过有限元热-结构耦合的分析方法对过焊孔焊缝处的焊接残余应力进行了数值模拟分析，结果表明：焊缝焊趾部位处存在较大的焊接残余拉应力，最大等效焊接残余应力有285 MPa，达到了材料屈服强度的82.6%，故在疲劳评估中应予以考虑.

2) 采用外推法对焊接细节的热点应力分析得到其应力集中系数为kt=1.92，表明过焊孔构造细节在起弧处存在较大的应力集中现象.

3) 根据所提构造细节S-N曲线计算流程，得到过焊孔构造细节的S-N曲线为

lgN=13.85-4.31 lgσ

其对应次数为200万次的疲劳强度为56.50 MPa，为此类钢桁梁主桁杆件疲劳寿命的评估提供指导.

[1] LEE C, CHANG K. Finite element computation of fatigue growth rates for mode I cracks subjected to welding residual stresses[J]. Engineering Fracture Mechanics，2011,78(13):2505-2520.

[2] DO V N V, LEE C, CHANG K. High cycle fatigue analysis in presence of residual stresses by using a continuum damage mechanics model[J]. International Journal of Fatigue，2015,70:51-62.

[3] 赵秋，吴冲.U肋加劲板焊接残余应力数值模拟分析[J].工程力学，2012(8):262-268.

[4] 卫军，汪东明，刘晓春，等.钢梁桥焊接残余应力的计算机模拟[J].桥梁建设，2015(4):94-99.

[5] 卫星，邹修兴，姜苏，等.正交异性钢桥面肋-板焊接残余应力的数值模拟[J].桥梁建设，2014(4):27-33.

[6] 刘沐宇，罗航.武汉二七长江三塔结合梁斜拉桥疲劳特性分析[J].武汉理工大学学报(交通科学与工程版)，2014(6):1193-1197.

[7] 管德清，吕黎明，杨勇，等.焊接结构疲劳强度预测的局部法研究[J].湘潭大学自然科学学报，2005(1):36-39.

[8] LOPEZ-JAUREGI A, ESNAOLA J A, ULACIA I, et al. Fatigue analysis of multipass welded joints considering residual stresses[J]. International Journal of Fatigue，2015,79:75-85.

[9] SAVAIDIS G, MALIKOUTSAKIS M. Advanced notch strain based calculation ofS-Ncurves for welded components[J]. International Journal of Fatigue，2016,83:84-92.

[10] BAUMGARTNER J. Enhancement of the fatigue strength assessment of welded components by consideration of mean and residual stresses in the crack initiation and propagation phases[J]. Welding in the World，2016,60(3):547-558.

[11] DING Y L, SONG Y S, CAO B Y, et al. Full-rangeS-Nfatigue-life evaluation method for welded bridge structures considering hot-spot and welding residual stress[J]. Journal of Bridge Engineering,2016,21(12):1158-1164.

Fatigue Performance Estimation of Structure Details Considering Welding Residual Stresses

LIUMuyuLUOHongjieDENGXiaoguang

(HubeikeylaboratoryofRoadwayBridgeandStructureEngineering,WuhanUniversityofTechnology,Wuhan430070,China)

Welded steel structure is widely used in the bridge engineering, but the welded joints lead to fatigue problems easily due to welding residual stress generated inevitably in the welding process. It is difficult to consider the real value of welding residual stress in the detailed classification of current specifications. Based on the Goodman formula and empirical theory, theS-Ncurve of material was modified by considering the welding residual stress quantitatively, and theS-Ncurve for welding joints was obtained. In this paper, welded detail with cope hole in truss oblique rod of the bridge girder is introduced as an example to demonstrate the detailed steps. With the analysis of coupled thermo-mechanical model, the numerical simulation of welding residual stress was conducted. In addition, the stress concentration factor was obtained by using extrapolation methods for hot spot stress. With the proposed method, theS-Ncurve of the welded detail with cope hole was determined, which can provide a guidance for accurately predicting the fatigue life and anti-fatigue design.

S-Ncurve; welding residual stress; Goodman formula; structure detail; welded detail with cope hole

U441

10.3963/j.issn.2095-3844.2017.05.001

2017-05-09

刘沐宇(1963—)，男，博士，教授，博士生导师，主要研究领域为桥梁工程

*国家自然科学基金项目(51378405)、中国工程院重点咨询研究项目(2016-XZ-13)资助