空间相关的非平稳地震动场合成思路及程序实现*
张 超 颜学渊 林进军
(福州大学土木工程学院 福州 350108)
空间相关的非平稳地震动场合成思路及程序实现*
张 超 颜学渊 林进军
(福州大学土木工程学院 福州 350108)
为了得到空间相关的非平稳地震动场,在分析地震动时频非平稳特性与相位差的关系及物理意义的基础上,推导了空间相关的非平稳地震动场的合成思路及简化分析方法:即通过功率谱矩阵进行CHOLESKY分解得到傅里叶幅值谱和相关相位角,基于相位差谱得到初始相位角,采用快速傅里叶变换得到时频非平稳的地震动场.基于此合成思路,编制了空间相关的非平稳地震动合成程序及交互式前后数据处理窗口.以某实际空间场地为算例,拟合得到了空间各支承点地震动时程.算例结果表明,本文编制的合成程序可以为多点激励地震响应分析提供空间相关的时频非平稳地震动场.
时频非平稳;相位差;空间相关地震动;合成程序
0 引 言
由于地震传播机制的复杂性,地面上各点的地震动互不相同,但又有一定的相关性.目前已有的空间地震动记录十分有限,无法满足特定场地的实际工程的抗震分析需求.因此,有必要建立空间相关地震动场合成方法,为各种场地下结构抗震分析提供地震动场输入模型.Hao等[1]首次提出空间相关的多点地震动合成方法,该方法基于随机相位角的单点地震波合成方法的基础上,考虑各个点地震动之间在空间效应.赵博等[2]则在理论推导的基础上,将不相干效应和行波效应单独考虑,对空间相关多点地震动合成方法进行简化.李英民等[3]在原Harichandran-Vanmarcke空间一维模型基础上,增加考虑了空间二维因素,该改进的相干模型可以较好地反映出地震动随频率、空间距离的变化规律.Bi等[4]提出以波动理论考虑不同场地土条件的改进方法.Konakli等[5]比较了分析采用桩-土单质点模型和土层一维波动理论合成的空间多点地震动.
近年的研究发现,实际地震动具有显著的时频非平稳特性,对于结构弹塑性反应具有重要影响,会使得地震动能量更为集中,进而导致结构发生更大程度的破坏[6].然而,目前基于[0,2π]均匀分布的相位谱合成的地震动不具有非平稳特性,即使后期乘以强度包络线,仍然无法模拟实际地震动的频率非平稳特性、震源机制、震级、传播效应,以及场地条件对非平稳特性的影响.因此,一些研究者在相位谱的基础上,进一步探讨了相位差谱或群延时与地震非平稳特性的关系.田玉基等[7-8]提出将相位差谱的统计模型引起空间相关非平稳地震动场的模拟方法之中.Zhang等[9]提出基于随机微分方程的群延时模型用于描述地震动的相位谱.代洪慧等[10]在传弦三角级数法的基础上,采用一定的穿零次数调频后的非平稳随机数作为相位角,合成符合目标反应谱的时频非平稳地震动时程.陈辉国[11]讨论了基于分频带子波瞬时谱模型的完全非平稳多点地震动模拟方法.
本文在研究地震动非平稳特性的基础上,采用相位差谱来考虑地震动的时频非平稳特性,推导基相位差谱的二维空间相关的地震动场合成公式,并基于MATLAB实现空间地震动场合成程序,实现时频非平稳的空间地震动合成,并编制了交互式输入和输出界面,为多点激励下的地震响应分析提供空间相关地震动输入.
1 相位差谱与非平稳特性的关系
地震动是非平稳的时间过程,表现在两个方面:一是强度非平稳,即时域非平稳特性,表现为地震动幅值先增后减;二是频率构成的非平稳性,即频域非平稳,表现为高频成分先到,低频成分随后.Ohsaki通过对发生在日本的49条基岩上的强震加速度记录研究发现:在[0,2π]上随机分布的相位谱之差具有一定的相关性.基于此,Ohsaki首次提出了相位差的概念,即相位谱中相邻两频率分量对应的相位差,表达式为
k=0,1,…,N-1
(1)
其研究发现非平稳地震动时程的相位差谱是非均匀分布的,其分布形状与强度包线非常相似.已有研究表明:相位差谱可以惟一地确定地震波的形状;而且,采用相位差谱可以直接反应地震波时频非平稳特性.然而,根据相位差的定义,相位差没有量纲,因此,其没有明确的数学意义.式(1)基础上,假设相位角是可微的,则可得
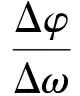
(2)
式中:dφ/dω为相位导数.
基于由式(2)得到的相位导数与相位差的线性关系,可以基于相位导数的概念来解释相位差谱的物理意义:相位差的均值可以反映了峰值发生的大致时刻;相位差的方差则反映了强震段的持续范围.这也就解释了相位差的分布规律对地震动时程的包络线形状和频率非平稳特性起着决定性的作用.相位差谱受到地震的幅值谱、相位谱及破裂过程、传播过程等多因素的影响,目前还无法精确的计算公式.目前,主要通过强震记录寻找相位差同震级和距离的关系,并进行经验估计.目前,相位差谱统计模型主要有朱昱模型、赵凤新模型、Thrainsson模型、山根尚志模型和李建波模型.
本文以某实际地震动合成算例说明基于相位差谱的时频非平稳地震动合成方法:福州市某大桥的实际工程场地土为IV类,震中距为50 km,目标拟合设防烈度为8度(取矩震级为6.5)的非平稳地震动时程.根据拟合要求,本文采用Thrainsson相位差谱的统计规律得到大幅值组、中间幅值组及小幅值组在归一化后的相位差分布函数.把各幅值组的相位差按照频率大小进行重新排列,得到相位差随频率的分布频数图及相位差随幅值的分布图,见图1;当取初相位角φ(0)=0,可计算得到相位角分布谱,见图2.可以看出相位角在[0,2π]上亦能满足均匀分布,此相位角分布与其他学者对相位角的统计规律相吻合.
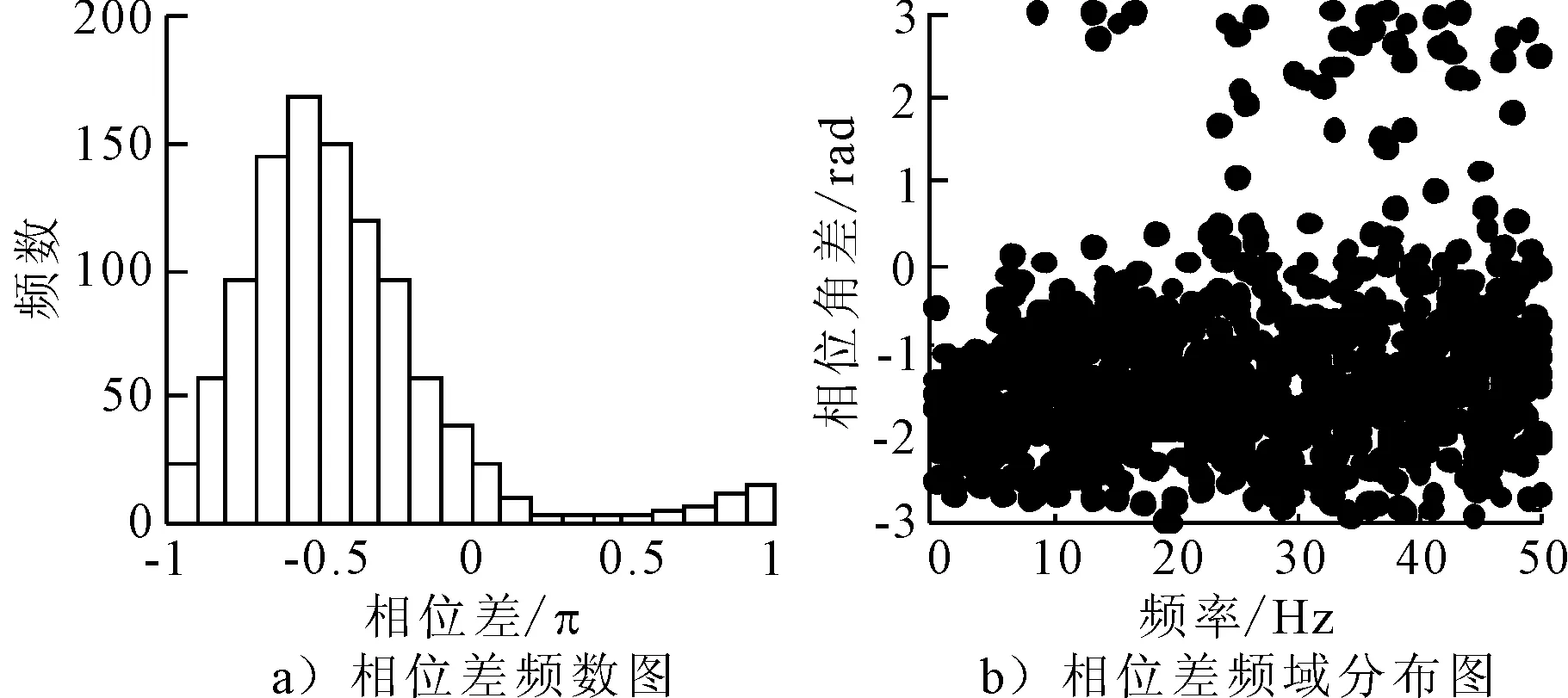
图1 相位差分布图
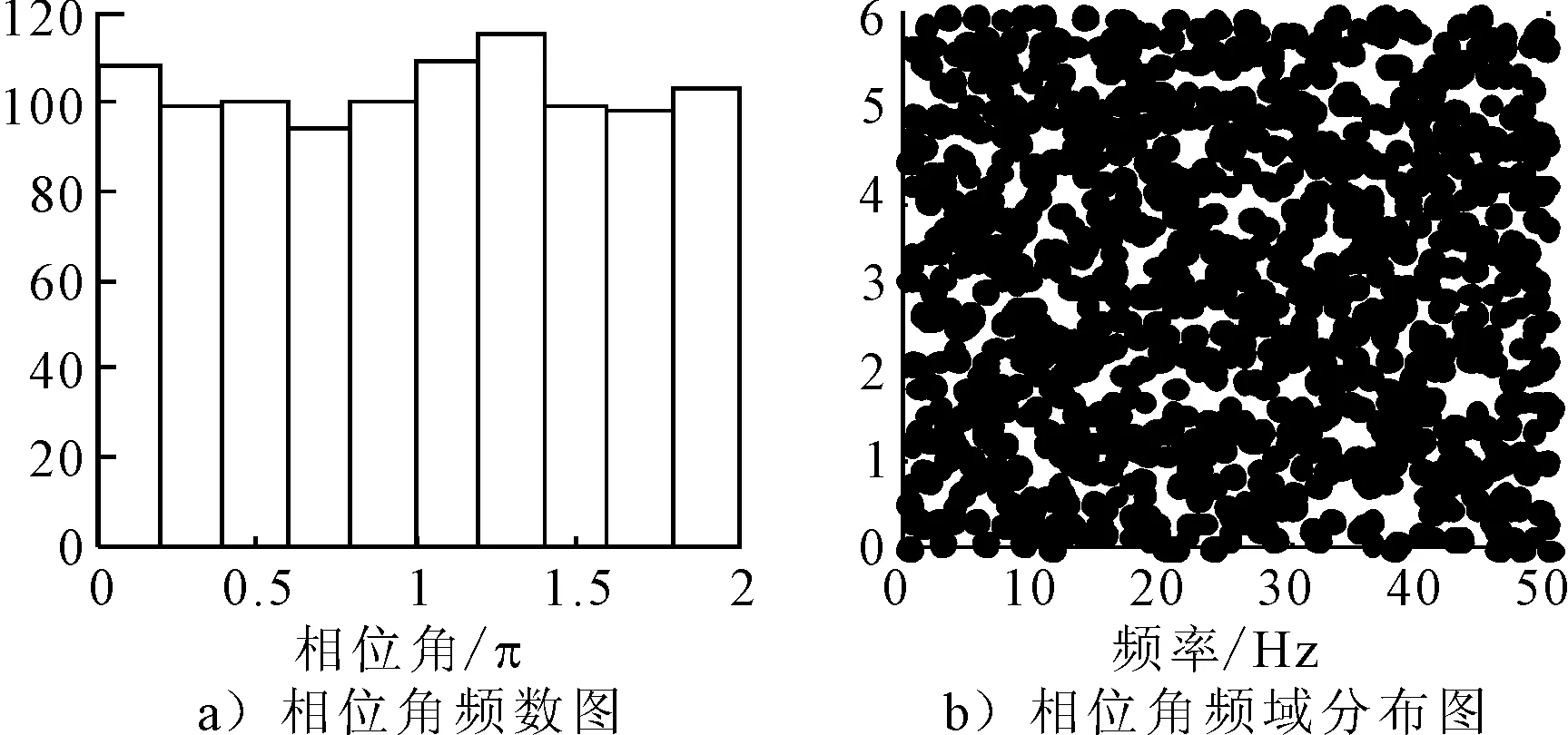
图2 相位角分布图
基于杜修力和陈厚群功率谱模型,计算得到傅里叶幅值谱,结合相位差谱模型得到的相位角谱,应用傅里叶逆变换即可得到的地震动加速度时程曲线与功率谱曲线,见图3.由图3a)可知,基于相位差谱合成的地震动时程,不需要人为乘以强度包络函数,即具有明显的时域非平稳特性.图3b)可知,拟合加速度时程功率谱与目标功率谱具有较好的吻合度.
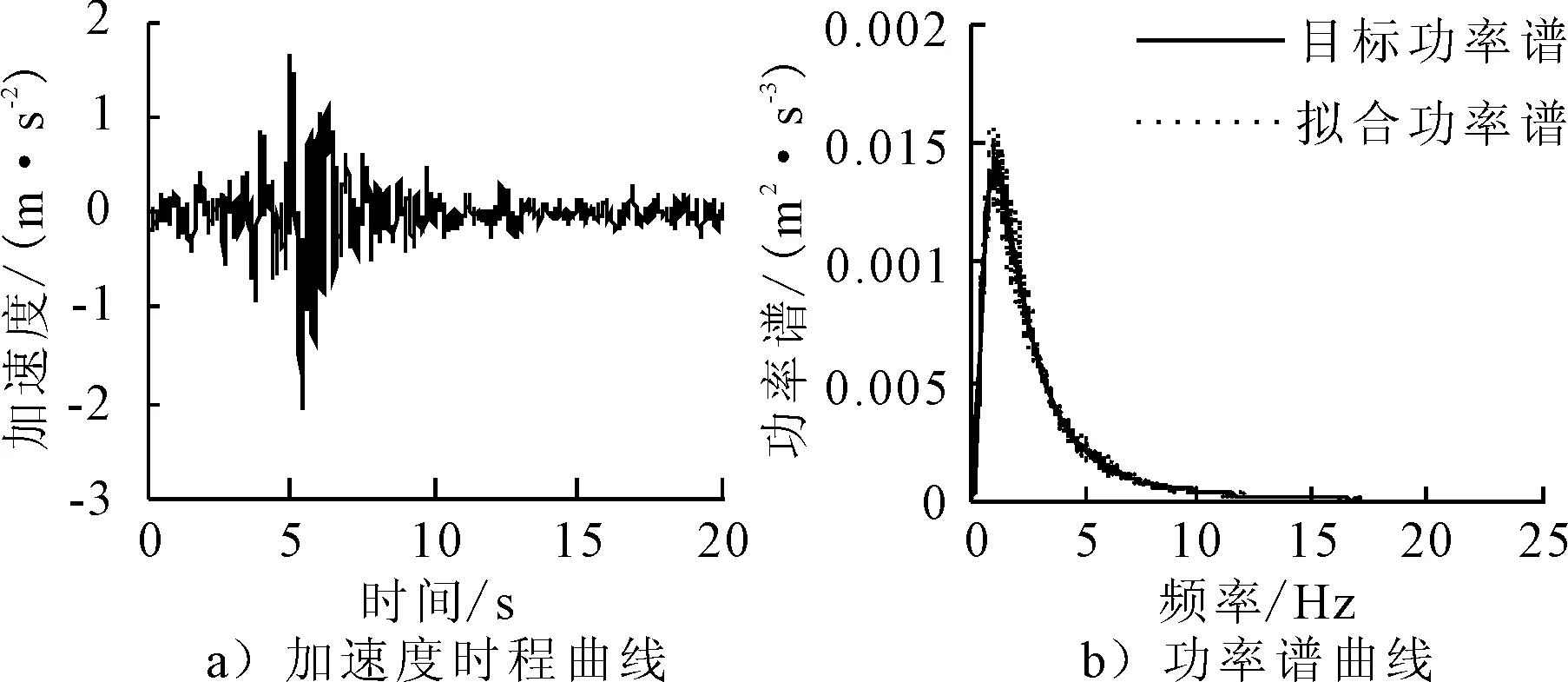
图3 基于相位差谱合成的非平稳地震动
2 空间相关的非平稳地震动场的合成思路
空间各支承点的地面运动可以认为均值等于零的随机振动过程,可用功率谱密度函数来表示.各支承点的功率谱函数矩阵为
(3)
式中:ωk为第k阶振型的自振频率;Sii(ωk)(i=1,2,…,n)为各支承点地面运动的自功率谱密度函数;Sij(iωk)(i≠j)为i,j两点之间的互功率谱密度函数,由自功率谱函数与相干函数γij(iωk)计算得到,其中i为虚数.计算公式为
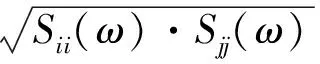
(4)
上式中的rij(iωk)写成矩阵的形式为
(5)
由于矩阵S(iωk)为实对称非负定矩阵,易于分解为一个下三角矩阵和转置的乘积,即进行CHOLESKY分解:
[S(iωk)]=[L(iωk)][L(iωk)]T
(6)
式中:
式中:
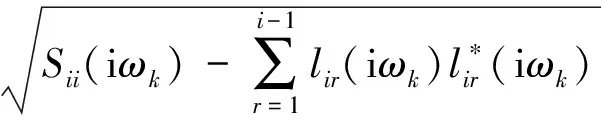
(8)
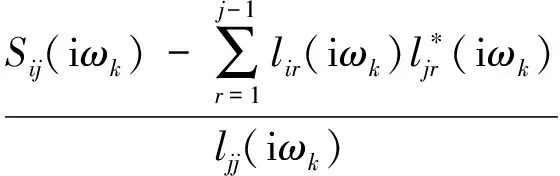
(i=j+1,…,n)
(9)
基于以上各式,可以根据下式求得空间各点地震动时程曲线
(10)
式中:φi(ωk)为ωk频率下,第i点地震动初始相位角;Aim(iωk),θim(ωk)为在ωk频率下,第i点地震动与第m个点地震动作用下的傅里叶幅值、相关相位角和初始相位角:
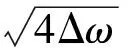
(11)
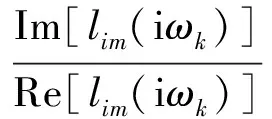
(12)
大量数据表明,初始相位角在[0,2π]区间内是均匀分布.为了使拟合得到的地震动时程具有时频非平衡特性,初始相位角的差值分布还需要符合相位差谱的统计规律.因此,根据拟合成地震动的震级、震中距及场地条件等各种因素,选用合适的相位差谱统计模型;基于相位差模型,得到初始相位角φi.
当按式(10)应用三角级数法求解时,ui(t)计算量十分巨大.快速傅里叶变换(FFT)采用‘一分为二’的思想,在频率合成上十分高效.为提高计算效频,式(10)采用快速傅里叶变换,变形为
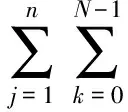
(13)
式中:
Bim(iωk)=Aim(iωk)/2
(14)
当不考虑各支承点的局部场地效应时,各点的地震动功率谱相同.可以把上文中的地震动合成公式进行简化,式(4)可以表示为
S(iωk)=S0(ωk)[exp(-iφ)]*[R]·
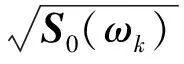
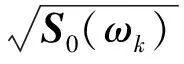
(15)
式中:
[R(iωk)]=[H(iωk)][H(iωk)]T
(16)
与式(4)进行对比可以发现
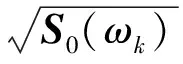
(17)
此时,
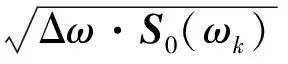
(18)
θim(iωk)=φim(iωk)
(19)
式(15)~(19)为不考虑局部场地效应时的地震动场合成公式的特例.式(18)体现了地震动的相干效应、式(19)体现了地震动在场地土中的传播效应.因此,地震动合成公式能够充分地考虑各支点的局部场地效应、波传播效应和空间失相干效应.同时,由相位差谱得到进行三角级数变化得到的地震动场具有显著的时频非平稳特性.
3 地震动场合成的程序实现
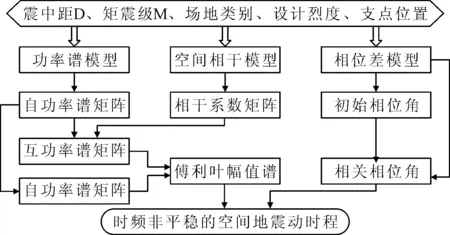
图4 空间非平稳地震动场合成思路
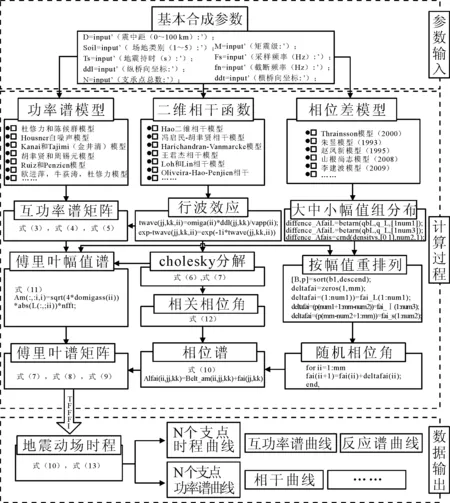
图5 合成程序编写流程
基于上文推导的空间地震动场计算公式,可以得到空间地震动场合成思路,见图4.根据上文的合成思路,本文编写了时频非平稳的空间多点地震动合成程序,具体的编制流程见图5.程序分为参数输入、中间计算及数据输出三个部分.在参数输入部分中,根据地震动的拟合目的,确定不同场地类别、震级大小、设计烈度震别等地震动设计参数.同时,可以选择不同的功率谱模型、相干模型及相位差谱模型.数据输出部分则可以得到拟合得到的各空间点的时频非平衡地震动时程,并可以进一步分析拟合地震动的功率谱、相干函数及功率谱等参数.
4 非平稳地震动场合成算例
已知二维空间四个支承点,其位置分布见图6.各点所处的场地类别均为中软土,土层平均剪切波速140≤vs≤250,属《公路桥梁抗震地设计细则》中Ⅲ类场地.需要拟合能考虑二维空间的相干效应,抗震设防烈度为8度的空间地震动场(其中矩震级为7级,震中距为80 km).本文拟合计算中,采样频率取为100 Hz,采样数量为2 048点.选用的功率谱、相位差谱及相干模型见表1.
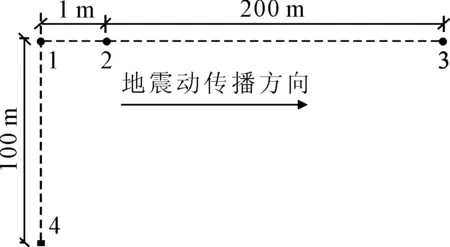
图6 各支承点平面位置示意图

表1 合成算例中选用模型
利用本文程序合成四个支承点时程曲线见图7.由图7可知,本文合成地震动时程均具有明显的时频非平衡特性.第1点和第2点的加速度时程对比可以发现,由于两个支承点的距离较近,两点地震动时程较相接近.各支承点拟合地震动时程的功率谱与目标功率谱比较见图8.由图8可知,合成时程的功率谱与目标功率谱吻合较好,本文程序的合成地震波具有与相应场地土适应的频谱特性.
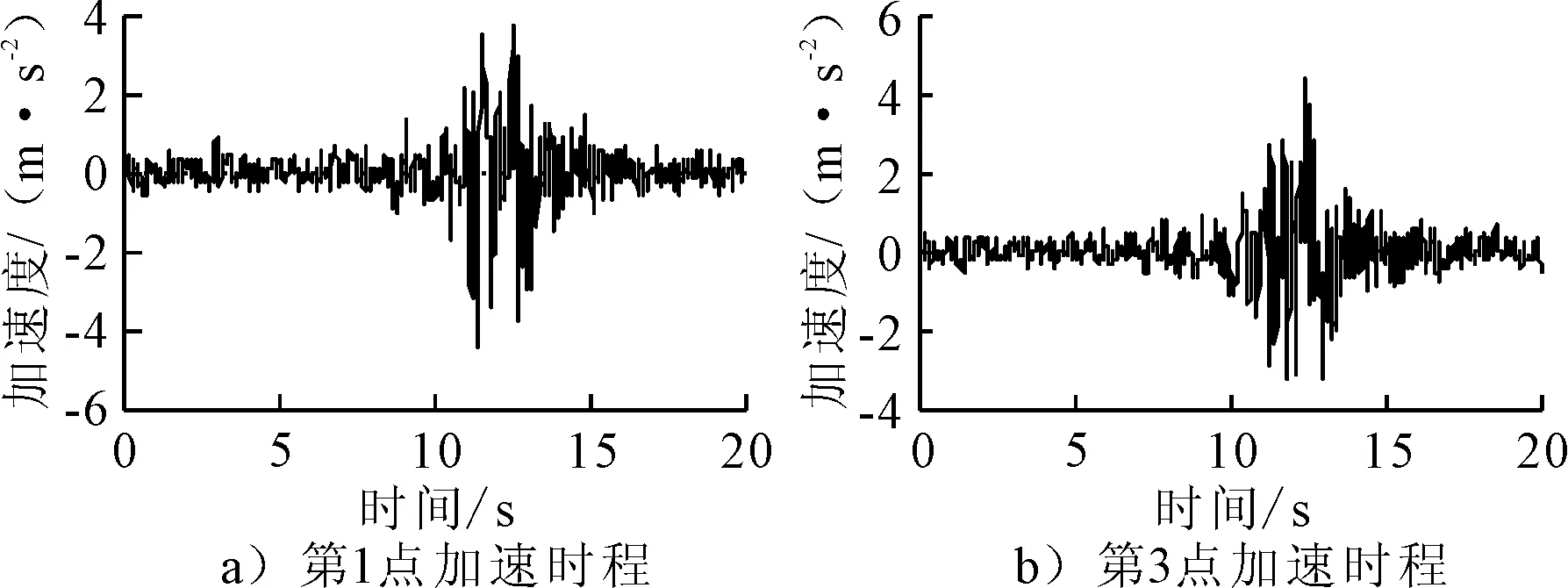
图7 各点加速度时程
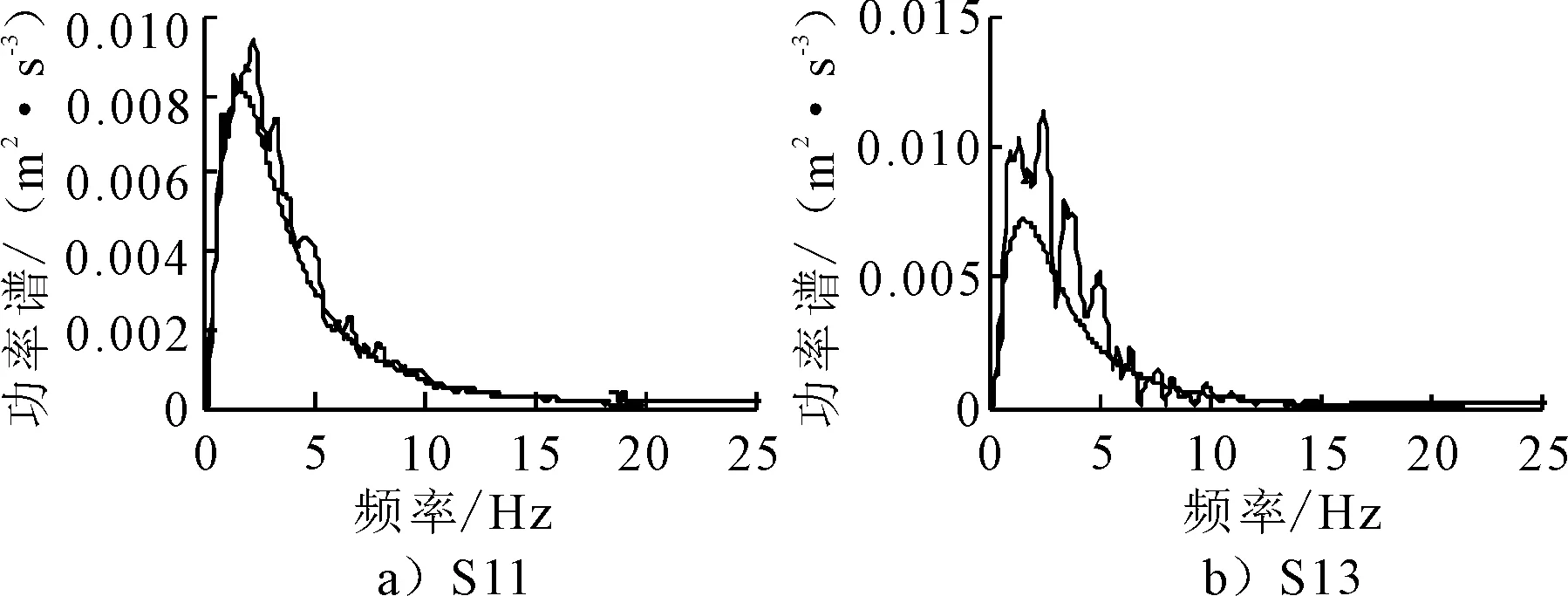
图8 地震动功率谱曲线
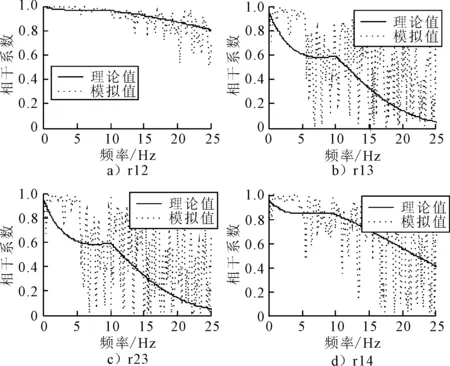
图9 地震动场相干系数
各支承点拟合地震动间的相干系数曲线见图9.通过与目标相干函数的对比可以发现,各条时程曲线间的相干系数与目标相干函数吻合较理想,合成各空间点的地震动时程能反映各支承点的二维空间相干效应.
5 结 论
1) 系统地分析了相位差谱对地震动非平稳特性的关系,根据其与相位导数的关系,明确相位差的物理意义;并以某实际算例说明基于相位差谱的合成方法可以得到时频非平稳的地震动时程,该方法不需要人为乘以强度包络函数.
2) 推导了考虑空间地震动的场地效应、波传播效应和失相干效应时频非平稳地震动场的合成思路,并基于快速傅里叶变换思路,对合成过程进行简化以提高计算效率.
3) 根据本文合成思路,编制了非平稳地震动场合成程序,并编写了“数据输入”和“数据输入”的交互式对话窗口,方便程序使用.
4) 通过某实际空间支承点为示例,应用本文地震动程序拟合得到目标场地各支承点的非平稳地震动.算例结果表明,本文的拟合思路及合成程序可以实现非平稳地震动场的拟合.
[1] HAO H, OLIVEIRA C S, PENZIEN J. Multiple-station ground motion processing and simulation based on smart-1 array data[J]. Nuclear Engineering and Design,1989,111(3):293-310.
[2] 赵博,石永久,江洋,等.一种空间相关多点地震动合成的实用模拟方法[J].天津大学学报(自然科学与工程技术版),2015,48(8):717-722.
[3] 李英民,吴哲骞,陈辉国.地震动的空间变化特性分析与修正相干模型[J].振动与冲击,2013,32(2):164-170.
[4] BI K, HAO H. Modelling and simulation of spatially varying earthquake ground motions at a canyon site with multiple soil layers[J]. Journal of Earthquake Engineering,2012,16(29):92-104.
[5] KONAKLI K D, KIUREGHIANV A. Simulation of spatially varying ground motions including incoherence, wave-passage and differential site-response effects[J]. Earthquake Engineering and Structural Dynamics,2012,41(3):495-513.
[6] 俞瑞芳,樊珂,彭凌云,等.地震动非平稳特性对结构反应影响的试验研究[J].土木工程学报,2010,43(12):13-20.
[7] 田玉基,杨庆山.基于相位差谱的空间相关非平稳地震动场的模拟[J].计算力学学报,2010,27(5):828-833.
[8] 杨娜,田玉基,杨庆山.与指定地震记录相关的非平稳地震动场的模拟[J].振动与冲击,2012,31(19):36-39.
[9] ZHANG C, SATO T, LU L. A phase model of earthquake motions based on stochastic differential equation [J]. Journal of Civil Engineering,2011,15(1):161-166.
[10] 代洪慧,张艳红,杨陈.基于调频率的时-频非平稳地震动生成[J].中国水利水电科学研究院学报,2013,11(1):8-13.
[11] 陈辉国.完全非平稳多点地震动模拟研究[D].重庆:重庆大学,2014.
Synthesis Thought and Program Realization of Non-stationary Spatially Variable Ground Motions
ZHANGChaoYUANXueyuanLINJinjun
(CollegeofCivilEngineering,FuzhouUniversity,Fuzhou350108,China)
This paper is aiming to synthesize Non-stationary Spatially Variable Ground Motions (NSVGMs). After analyzing the relationship between time-frequency non-stationary characteristics and phase differences, the simulating method of Non-stationary Spatially Variable Ground Motions (NSVGMs) is proposed in this paper. In the simulation progress, amplitudes and related phases are calculated from the CHOLESKY decomposition of the power spectrum matrix, and the initial phase is obtained from the phase differences spectrum. Then the NSVGMs are synthesized by IFFT method. Based on the proposed method, a program to synthesize NSVGMs with interactive interface is compiled. Finally, a series NSVGMs of certain spatial sites are synthesized by this program. Results of the computational example show that this synthesis program can effectively provide NSVGMs for multi-excitation seismic analysis.
non-stationary; phase difference; spatially variable ground motions; synthesis program
U448.25
10.3963/j.issn.2095-3844.2017.05.006
2017-07-22
张超(1985—):男,博士,副教授,主要研究领域为大跨结构抗震及减震措施
*国家自然科学基金项目(E51508102)、教育部博士点基金项目(20133514120006)、福建省教育厅基金(JK2014005)资助

