线性磁场作用下一维铁磁链的孤子激发

莫子杰, 陈 浩, 王瑞强

(华南师范大学物理与电信工程学院, 广东省量子调控工程与材料重点实验室， 广州 510006)

线性磁场作用下一维铁磁链的孤子激发

莫子杰, 陈 浩*, 王瑞强

(华南师范大学物理与电信工程学院, 广东省量子调控工程与材料重点实验室， 广州 510006)

研究了在线性磁场作用下，一维铁磁链的2种孤子激发. 分别导出2个不同修正的非线性薛定谔方程，可以得到各自所激发的孤子解. 此2种孤子激发结果均表明，在增加线性磁场后，孤子的外形与有效质量并不受到影响，但孤子的运动模式却发生改变，从一般的匀速运动变为匀变速运动. 而且在线性磁场作用下孤子的能量出现了定域分布，随位置的不同而不同. 由此发现，引入线性磁场的普遍意义在于，可使一维铁磁链中的孤子激发和移动受到更好的控制，同时不破坏孤子的稳定性.

一维铁磁链； 孤子； 线性磁场； 非线性薛定谔方程

Keywords： 1D ferromagnetic chain; soliton; linear magnetic field; nonlinear Schrödinger equations

一维铁磁链在凝聚态物理研究中非常重要，拥有自旋相互作用的一维海森堡铁磁链，在考虑高阶非线性相互作用时，可激发出孤子[1-5]. 通常研究易平面相互作用[6]、DM 相互作用[7]、单离子各向异性[8]等在铁磁链中对非线性激发的影响. 随着研究的深入，考察的相互作用越来越多，如考察系统本身的自相互作用[9-13]以及外界因素对一维铁磁链非线性激发的影响[14-18].

本文考虑外加线性磁场，建立一维铁磁链的孤子激发模型，探讨线性磁场对激发的影响. 首先提出该模型的哈密顿量，推导出系统第一种孤子模型的动力学方程；然后运用扩展的行波法，求解出在线性磁场作用下，一维铁磁链的孤子解；再根据孤子解分析孤子的特性、运动特征及其能量分布，与无磁场的情况下相比较，研究线性磁场对孤子的实质性影响；最后求解第2种孤子激发，并做相应的讨论.

1 含非均匀外磁场的一维铁磁链系统

在非均匀外磁场作用下，一维铁海森堡磁链的哈密顿量可写为[19]

(1)

通过Holstein-Primakoff变换[20],式(1)可改写为由玻色算符组成的哈密顿量

(2)

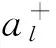
引入相干态变换使方程变为自旋概率幅的运动方程，设相干态|a〉满足al|al〉=al|al〉[21](αl为在l格点上的自旋概率幅)，可得

(3)

假定孤子的空间宽度远大于晶格常数r0，由此可采用空间连续近似处理式(3)，即

(4)

将式(4)代入式(3)，经整理可得到一个修正的含空间变系数的非线性薛定谔方程

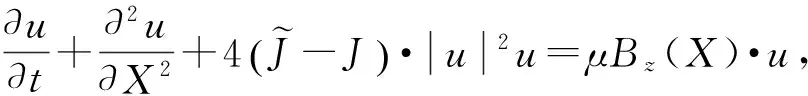
(5)

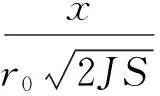
对于修正的非线性薛定谔方程，一般很难找到精确解析解，只有在某些特殊的情况下才有解. 非线性薛定谔方程在各种修正情况下求解的情况也被广泛研究[22-24].

2 线性磁场下的孤子求解

考虑一维线性的外磁场Bz(x)=B0+B1x，即

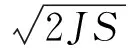
(6)

其中，B0和B1为描述磁场的常系数. 对于类似于式(5)的修正非线性薛定谔方程，文献[22]运用逆散射方法研究其解. 为了得出方程(6)的解，本文采用扩展的行波法求解. 设

u=φ(ξ)·eiθ(ξ,t),

(7)

其中，φ和θ均为实函数；ξ=X-f(t)描述扩展的行波运动；f(t)是一个关于时间的单变量实函数.

将式(6)、(7)代入式(5)可得

(8)

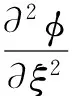
(9)

为求解孤子波，可先求解相位θ. 根据边界条件要求，孤子在无穷远处要趋于0，即当ξ→±∞时，φ→0，因此将式(8)整理后代入边界条件可得

(10)

其中，g(t)为待定实函数. 利用式(10)代换式(9)中含θ的项，可得

(11)

其中，

方程(11)的一般通解难以求解，于是可令k(ξ,t)为一个常数，方程(11)的形式则是一个椭圆微分方程. 由此可解得

其中，x0、g0、v、C均为常数，可由初始条件和归一化条件决定.

3 孤子解的分析及讨论

3.1 孤子的解

根据方程(11)可得椭圆方程并求其孤子解

(12)

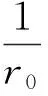
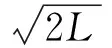
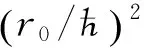
(13)

3.2 孤子的运动情况

与一维铁磁链中的孤子激发结果[19]比较，在引入了线性磁场后，孤子的宽度和峰值不变，即孤子保持了它在无外场下的外形特征. 然而孤子的运动情况发生了很大改变. 根据运动学规律，从式(13)中双曲正割函数可以发现，孤子的运动不再是通常的匀速运动，而是具有一定初速度的匀变速运动. 孤子的初速度为

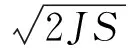
(14)

孤子运动的加速度为

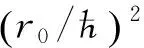
(15)

由此可得孤子运动的(瞬时)速度为

(16)

这里与无线性磁场作用下的孤子运动情况不同，v不再是匀速的，而是孤子匀变速运动的初速度. 此时孤子的运动速度是一个随时间线性变化的量，同时也是孤子波的群速度. 由式(15)可知，孤子运动的加速度与铁磁链中的交换积分及线性磁场的线性项有关. 对于同一条铁磁链来说，其上激发的孤子运动加速度的大小恰与B1成正比，方向也取决于B1. 综合来看，线性外磁场具有改变孤子运动状态的作用.

当磁场的线性项不存在时(B1=0)，孤子并没有加速，即匀速行波孤子(图1A). 当加入了线性磁场后(B1=0)，即使孤子被激发时无初速度，它也会在外磁场的推动下做匀加速运动(图1B). 另外，初速度和磁场将同时影响孤子的运动轨迹，如在图1C中，由于初速度和加速度方向相同，所以孤子沿某个方向匀加速运动；而在图1D中，初速度取负值时，表示与选定的正方向相反，由于初速度与加速度的方向相反，所以孤子先减速后沿着加速度的方向做反向加速的运动. 此时孤子的运动方向被线性磁场改变并最终沿着某一方向匀加速运动. 可见，线性外磁场改变了孤子的运动性质，使其运动更依赖于外界而非初始条件. 当孤子被激发后，可通过调节磁场的线性项B1来有效控制孤子的运动情况. 这样做不但丰富了孤子的传播模式，而且孤子原本的激发外形特征不会受到改变和破坏.

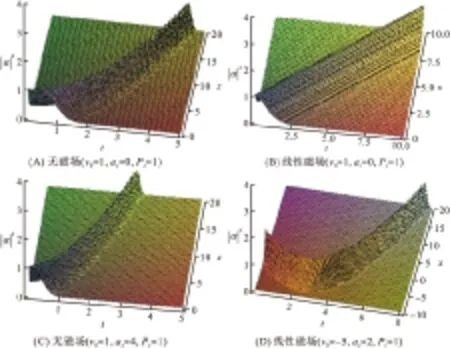
图1 在有无线性磁场条件下一维铁磁链中的孤子运动

Figure 1 Soliton motion in 1D ferromagnetic chain with and without linear magnetic field

3.3 孤子的能量

为求解此孤子能量，定义孤子的广义频率，即频移Ω=∂Θ/∂t. 可以证明，Ω是不随时间改变的量，即有dΩ/dt=0成立[22]. 频移有表征能量的性质，于是可将孤子的能量表示为

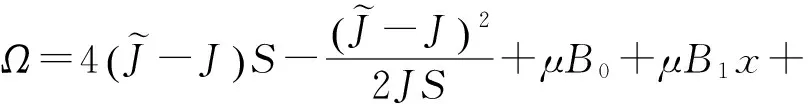
(16)

其中孤子无磁场下的静能量为

线性磁场提供给孤子的能量为

EB=μB0+μB1x，

(17)

为了进一步分析能量在孤子上的分布，可将Es改写为

Es=EB0+μB1ξ,

(18)

图2 线性磁场下一维铁磁链的孤子概率幅|α|及能量Es分布

Figure 2 Soliton probability amplitude (|α|) and energy distribution (Es) of one dimensional ferromagnetic chain under linear magnetic field

注：参数C=1,Ps=1,EB0=-1,μB1=2.5.

最后应当注意到，Es描述孤子能量的局域性分布情况. 孤子的移动也是能量的传播，所以孤子自身所传递的总能量应为

表明了孤子所传递的能量其实就是激发能. 它并没有受到线性磁场线性项B1的影响，所以，线性磁场作用下一维铁磁链激发的孤子依然能够在链上稳定传播，B1的存在并没有为孤子能量传输增加负担.

4 线性磁场下的改进孤子解

一维铁磁链的非线性激发是丰富的，文献[26-27]提出了铁磁链中存在的1个改进孤子解，并研究了Aharonove-Bohm磁通对其孤子激发的影响，这种改进孤子的形式后来被广泛运用于其他模型的求解.

运用相同的哈密顿量式(1)及Holstein-Primakoff变换，并且引入相干态和空间连续近似，并设线性磁场满足式(6)，将式(4)、(6)代入式(3)，可以得到一个新的含空间变系数的非线性微分方程

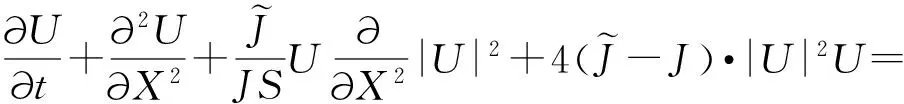
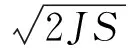
(19)

U=Φ(η)·eiϑ(η,t),

(20)

其中，Φ和相位ϑ均为实函数；η=X-F(t)描述扩展的行波运动；F(t)是一个关于时间的单变量实函数. 将式(20)代入式(19)中，经过整理运算，可得

(21)

其中h(t)为待定实函数，即

(22)

其中，

(23)

方程(22)是一个复杂的非线性方程，可求得当K(η,t)为常数时的解. 于是设K(η,t)=C′，C′为常数. 基于此，由式(21)、(23)易得F(t)、h(t)及相位的表达式. 而方程(22)的解则为

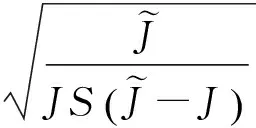
2(η-η0),

其中，η0为常数，由初始条件决定. 等号左端的第2项可以近似为常数，可归入η0中，从而可以得到方程(22)的一个近似孤子解[26-27]. 结合归一化条件，最后可得常数C′的值及一维铁磁链在线性磁场作用下的改进孤子解

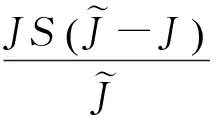
(24)

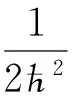
(25)

同样，式中g0、v均为常数，其具体取值由初始条件决定. 式(24)这个孤子只有在各向异性的铁磁链中才存在，并且依然是一个可以稳定传播的孤立子. 容易判断，孤子的外形即宽度和峰值都没有受到线性磁场的影响. 改进后的孤子依然具有宽度变窄、峰值更高的特点[26]，而这些是由于只考虑了不同的非线性相互作用而造成. 从双曲余弦函数内的表达式可以看出，加入线性磁场后，该改进孤子的运动规律与式(13)孤子的运动规律一样，具有相同的初速度(式(14))、加速度(式(15)). 这里可以看出线性磁场对孤子的产生及稳定性并没有任何影响，而仅起到改变它运动模式的作用.

通过式(25)可以考察这个改进孤子的能量分布. 设此处孤子的频移量为Ω′=∂Θ′/∂t，同理可以证明dΩ′/dt=0，于是能量为

5 结论

受外场影响的物理系统是普遍存在的. 本文首先推导出一维铁磁链在非均匀外磁场中，自旋概率幅的运动方程，进而研究了在线性磁场作用下2种情况的孤子激发，发现它们仍然能够激发出稳定地孤子，但此时孤子的相位和运动情况上发生了变化. 孤子的激发特征量，如峰值、宽度和有效质量这些均由非线性相互作用决定，与外加的线性磁场无关. 而外加的线性磁场对铁磁链孤子的影响都体现在其运动状态和能量的转化上. 线性磁场的存在破坏了系统原有的平移对称性，使得铁磁链中激发的孤子做匀变速运动，而且最终运动方向取决于加速度的方向，由此使得孤子能量呈现定域分布，然而其传输的总能量大小却不会受到磁场线性项的影响. 孤子的运动减少了对初始条件的依赖，增强其运动的可控性，同时又不会为孤子的传播带来负面影响.

[1] PUSHKAROV D I,PUSHKAROV K I. Solitary magnons in one-dimensional ferromagnetic chain[J]. Physics Letters A,1977,61(5):339-340.

[2] PUSHKAROV D I,PUSHKAROV K I. Solitons in one-dimensional ferromagnetic systems[J]. Physica Status Solidi,1977,81(81):703-707.

[3] MIKESKA H J,OSANO K. Dynamics of the soliton instabi-lity in the easy-plane ferromagnetic chain[J]. Zeitschrift Für Physik B:Condensed Matter,1983,52(2):111-116.

[4] BALAKRISHNAN R,BISHOP A R. Nonlinear excitations on a quantum ferromagnetic chain[J]. Physical Review Letters,1985,55(5):537-540.

[5] 熊化高,陈浩. 考虑近邻作用下的一维铁磁链中的孤子[J]. 华南师范大学学报(自然科学版),2007(4):66-70.

XIONG H G,CHEN H. The soliton in the one-dimensional ferromagnetic chains with N-neighbor interactions[J]. Journal of South China Normal University (Natural Science Edition),2007(4):66-70.

[6] DANIEL M,AMUDA R. Nonlinear dynamics of weak ferromagnetic spin chains[J]. Journal of Physics A: Gene-ral Physics,1998,28(19):5529-5537.

[7] KUMAR P,SAMALAM V K. Solitons in an easy-plane ferromagnetic chain[J]. Journal of Applied Physics,1982,53(3):1856-1857.

[8] 翁紫梅,陈浩. 单离子各向异性影响下的一维铁磁链中的孤子[J]. 物理学报,2007,56(4):1911-1918.

WENG Z M,CHEN H. Solitons in a one-dimensional ferromagnetic chain under the influence of single-ion anisotropy[J]. Acta Physica Sinica,2007,56(4):1911-1918.

[9] TANG B,LI D J,TANG Y. Quantum breathers in Heisenberg ferromagnetic chains with Dzyaloshinsky-Moriya interaction[J]. Chaos,2014,24(2):023113.

[10] PRIMATAROWA M T,KAMBUROVA R S. Dark solitons in ferromagnetic chains with first- and second-neighbor interactions[J]. Central European Journal of Physics,2012,10(5):1102-1108.

[11] HUANG G,JIA Z. Self-induced gap solitons in Heisenberg ferromagnetic chains[J]. Physical Review B,1995,51(1):613-616.

[12] WANG P. Conservation laws and solitons for a generalized inhomogeneous fifth-order nonlinear Schrödinger equation from the inhomogeneous Heisenberg ferromagnetic spin system[J]. European Physical Journal D,2014,68(7):1-8.

[13] DMITRIEV D V,KRIVNOV V Y. Magnetic solitons in a frustrated ferromagnetic spin chain[J]. Physical Review B,2010,81(5):054408.

[14] 陈浩,陈渊. Aharonove-Bohm磁通对一维铁磁链中孤子的影响[J]. 物理学报,1996,45(8):1249-1254.

CHEN H,CHEN Y. Effect of the Aharonov-Bohm flux to the soliton in a one-dimensional ferromagnetic ring[J]. Acta Physica Sinica,1996,45(8):1249-1254.

[15] LI D J,TANG Y. Interactions between the time-varying electromagnetic field and the quantum solitary wave in a ferromagnetic chain[J]. Modern Physics Letters B,2012,26(24):1250160.

[16] LI Z D,LI L,LIANG J Q. Soliton collision in a ferromagnetic spin Chain driven by a magnetic field[J]. Chinese Physics Letters,2004,21(3):443-446.

[17] KAVITHA L,SARAVANAN M,GOPI D. Propagation of an electromagnetic soliton in an anisotropic biquadratic ferromagnetic medium[J]. Chinese Physics B,2013,22(3):030512.

[18] VEERAKUMAR V,DANIEL M. Electromagnetic soliton damping in a ferromagnetic medium[J]. Physical Review E,1998,57(1):1197-1200.

[19] 李正中. 固体理论[M]. 2版. 北京:高等教育出版社,2002:86-88.

[20] HOLSTEIN T D,PRIMAKOFF H. Field dependence of theintrinsic domain Magnetization of a Ferromagnet[J]. Physical Review,1940,58(12):1098-1113.

[21] GLAUBER R J. Coherent and incoherent states of the radiation field[J]. Physical Review,1963,131(6):2766-2788.

[22] CHEN H H,LIU C S. Solitons in nonuniform media[J]. Physical Review Letters,1976,37(37):693-697.

[23] SERKIN V N,AKIRA H,BELYAEVA T L. Nonautonomous solitons in external potentials[J]. Physical Review Letters,2007,98(7):074102.

[24] SCHARF R,BISHOP A R. Properties of the nonlinear Schrödinger equation on a lattice [J]. Physical Review A,1991,43(12):6535-6544.

[25] CORDEIRO C E,MOURA M A D. Solitary waves in an isotropic ferromagnetic chain[J]. Physics Letters A,1978,66(4):332-333.

[26] CHEN H,CHEN Y. Influences of the Aharonov-Bohm flux on the improved soliton in a one-dimensional ferromagnetic ring[J]. Communications in Theoretical Physics,1998,30(2):173-270.

[27] 陈浩，黄皙恒，谢元栋. 一维铁磁链的一个改进孤子解[J]. 华南师范大学学报(自然科学版),2002(2):5-8.

CHEN H,HUANG X H,XIE Y D. An improved soliton in a one-dimensional ferromagnetic chain[J]. Journal of South China Normal University (Natural Science Edition),2002(2):5-8.

Solitons in One-Dimensional Heisenberg Ferromagnetic Chain with Linear Magnetic Field

MO Zijie, CHEN Hao*, WANG Ruiqiang

(Guangdong Provincial Key Laboratory of Quantum Engineering and Quantum Materials, School of Physics and Telecommunication Engineering, South China Normal University, Guangzhou 510006, China)

Two kinds of soliton excitations in 1D ferromagnetic chain with linear magnetic field are considered. By solving two different modified nonlinear Schrödinger equations, the soliton solutions excited by them are obtained. The two obtained soliton solutions show that linear term of magnetic field has no influence on the shape and effective mass of each soliton, but changes the motional mode from uniformly motion to uniformly variable motion. Moreover, the energy of soliton appears the localized distribution after introducing the linear magnetic field. Introducing linear magnetic can make the excitation and motion of soliton more controllable without destroying the stability in 1D ferromagnetic chain.

2015-12-31 《华南师范大学学报(自然科学版)》网址：http://journal.scnu.edu.cn/n

国家自然科学基金项目(11474106)

*通讯作者:陈浩，教授，Email:chenhao@scnu.edu.cn.

O482.51；O175.14

A

1000-5463(2017)05-0016-06

【中文责编：谭春林 英文审校：肖菁】